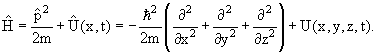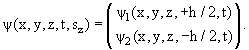Квантовая механика – теория, описывающая квантовые частицы, движущиеся со скоростью много меньшей скорости света с. Связь между операторами в квантовой механике имеет тот же вид, что и в классической физике. Так полной энергии частицы E, состоящей из кинетической T_кин и потенциальной U_пот энергий,

в квантовой физике соответствует оператор полной энергии (оператор Гамильтона)

    Временная эволюция системы в квантовой физике в нерелятивистском случае описывается уравнением Шредингера

являющимся аналогом уравнения Ньютона в классической физике. Если потенциал U не зависит от времени t U = U(x,y,z), то решение уравнения Шредингера имеет вид

где E – полная энергия квантовой системы, а волновая функция ψ(x,y,z) удовлетворяет стационарному уравнению Шредингера

    Наряду с такими привычными из классической физики величинами как энергия, импульс в квантовой физике появляются величины, не имеющие аналогов в классической физике. Одной из таких величин является спин – собственный механический момент частицы. Понятие спина было введено в квантовую физику в 1925 г. Дж. Уленбеком и С. Гаудсмитом на основе анализа спектров атомов. Для правильного писания наблюдаемых спектров атомов электрону было необходимо приписать ещё одно квантовое число s. Квантовое число спина электрона s = 1/2.
    Волновая функция частицы со спином зависит не только от её трех пространственных координат и времени, но и от спина, характеризующего внутреннее состояние частицы. Так же как и в случае полного момента количества движения одновременно можно измерить только квадрат полного спина и одну из его проекций на произвольную ось. Две проекции на разные оси одновременно не имеют определенные значения. Обычно в качестве проекции спина выбирают проекцию на ось z, определяемую условиями проведения измерений. В отличие от пространственных координат спиновая переменная может принимать лишь дискретные значения. Для частицы, имеющей значение квантового числа спин s = 1/2 проекция спина s_z может принимать два значения s_z = ±1/2. Поэтому волновую функцию ψ(x,y,z,t,s_z) обычно записывают в виде столбца, имеющего две строки

    При s = 1/2 матрицы квадрата полного спина и его проекции на ось z имеют вид

Матрицы ŝ_x и ŝ_y в этом представлении имеют вид

.

Матрицы _x, _y, _z называются матрицами Паули.

Пол Дирак (1902–1984)

Эрвин Шредингер (1887 – 1961)

   Де Бройль выдвинул теорию, в которой устанавливалась связь между частицами и волнами. Это была очень стройная теория и она сразу привлекла меня своей красотой. Частицы и волны были связаны релятивистским образом, причем так, что при стремлении масс покоя частиц к нулю, получалось соотношение между квантами света и электромагнитными волнами. Восхищенный красотой работы де Бройля, я, тем не менее, не мог воспринимать волны всерьез. Я всецело пребывал во власти теории Бора и предложенные им орбиты понимал совершенно буквально – электроны были реально существующими частицами, а волны де Бройля представлялись мне просто математической выдумкой, совершенно не существенной для физиков. Моя точка зрения была, конечно, совершенно неправильной. Работу де Бройля прочитал Шрёдингер. У Шрёдингера был иной подход и он получил другое образование. Он хорошо изучил собственные функции и собственные векторы, о которых я не знал совсем ничего. Поэтому Шрёдингер со своим взглядом на мир сумел развить идеи де Бройля и получить блестящий результат. Примитивные формулы де Бройля, которые годились только для описания свободных частиц, Шрёдингер распространил на частицы, движущиеся в электромагнитном поле, что привело его к волновой механике.

П. А. М. Дирак. «Воспоминания о необычной эпохе»

Нобелевская премия по физике

1933 г. – Э Шредингер и П. Дирак. За открытие новых плодотворных формулировок атомной теории.