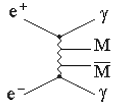
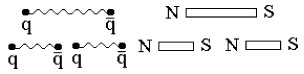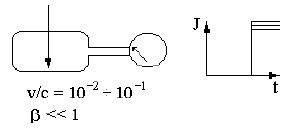16 Экзотические частицы

    К экзотическим следует отнести частицы, которые обладают нестандартными свойствами и пока не обнаружены, но входят в различные теоретические модели: Хиггс-бозоны, суперсимметричные частицы, магнитные монополи, тахионы, аксионы, WIMP-частицы.

16.1 Хиггс-бозоны

    В электрослабой теории спонтанное нарушение симметрии, т.е. появление наряду с безмассовыми фотонами массивных W±- и Z0-бозонов, связывают с существованием механизма Хиггса, реализуемым через поля Хиггса. Поиск Хиггс-бозонов является основной задачей на действующих и строящихся ускорителях частиц. В Стандартной Модели физики частиц предполагается существование скалярного хиггсовского бозона. На ускорителе LEP сделана попытка обнаружения рождения Хиггс-бозона в реакции е+ + е- → Z0 + Н0. В эксперименте было поставлено ограничение на массу mH0 > 100 ГэВ. В расширенной Стандартной Модели предполагается существование заряженных Хиггс-бозонов. Массы Хиггс-частиц не предсказываются в теориях, однако делается предположение, что масса Хиггс-бозона не может быть больше 300 ГэВ. Большие надежды возлагаются на открытие хиггcовских полей, которые могли бы войти в состав физического вакуума.

16.2     Суперсимметричные частицы (SUSY-частицы)

    Дальнейшее расширение Стандартной Модели предусматривает введение нового вида симметрии. Эта симметрия предполагает, что каждому фермиону (спин 1/2) должен соответствовать бозон (спин 1). Суперпартнеры обычных частиц приобретают в названии окончание -ино, например, фотон − фотино, гравитон − гравитино, бозон Хиггса − хиггсино. SUSY-партнер кварка называют скварк, а лептона − слептон.
    Для характеристики суперсимметричных частиц вводится новое квантовое число, называемое R-чeтность. Для обычных частиц R = +1, для супсрсимметричных частиц R = − 1, причем
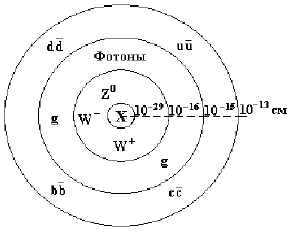
R = (-1)3B+L+2J, где B − барионное число, L − лептонное число и J − спиновое квантовое число. Предполагается, что R-четность сохраняется в электрослабых взаимодействиях. Благодаря сохранению R самая легкая суперсимметричная частица должна быть стабильной, поэтому она представляет интерес как кандидат на роль частицы темной материи.(см. п. 2.2).

16.3 Магнитные монополи

    Квантовая электродинамика справедлива в очень широких пределах от 2·10-16 см до 5·1010 см (80 радиусов Земли), т.е. ~ 25 порядков. Однако в ней имеются нерешенные вопросы.

  1. Почему квантуется электрический заряд?
  2. Чем определяется значение электрического заряда и величина массы электрона?
  3. Чем определяется количество заряженных лептонов?
  4. Почему взаимодействие фотонов с адронами не описывается электродинамикой и приходится прибегать к модели векторной доминантности − превращению фотона в векторный мезон g, который сильно взаимодействует с адроном?

  1. Для объяснения процесса глубоконеупругого рассеяния лептонов на адронах: е + р → h + е + р приходится вводить кварковую стадию и строить квантовую хромодинамику.
  2. Проблема монополя может быть решена только в случае, если он будет обнаружен в эксперименте.

    В классической электродинамике магнитное поле создается магнитными диполями и нет монополей. Это утверждение содержится в уравнениях Максвелла

div E = 4πρе,
div B = 0,

    В этих уравнениях отсутствует магнитный заряд. В 1931 году Дирак предположил, что вместо второго уравнения можно написать уравнение в виде

div B = 4πρm,

где ρm − плотность магнитного заряда. Так был введен в рассмотрение монополь Дирака. Если на расстоянии b от него движется частица со скоростью v, то действующая на эту частицу сила Лоренца

и частица получит импульс

Изменение импульса частицы связано с изменением углового момента

Т.к. орбитальный угловой момент L = nћ квантуется, то отсюда вытекает квантование электрического заряда

n = 0, ±1, ±2,...,

а магнитный заряд

    Швингер показал, что отсюда можно получить следующие заключения.

  1. Существование магнитного монополя объясняет квантование электрического заряда.
  2. Можно получить величину магнитного заряда. Таким образом, безразмерная константа взаимодействия двух монополей g получается очень большой

    Это обстоятельство позволяет рассмотреть аналогию между взаимодействием монополей и сильным взаимодействием. При разрыве магнитного диполя не возникает магнитный монополь, а снова образуются диполи. То же происходит при разрыве кварковой струны − образуются дикварковые струны и не удается выделить отдельный кварк (рис. 108).


Рис. 108: Аналогия между магнитными диполями и парами кварков.

    На опыте не наблюдается изолированный монополь, возможно из-за огромной силы, действующей между монополями.


Рис. 109. Структура GUT-монополя.

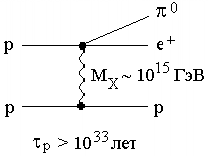
    В 1974 году Г. т'Хофт и А.М. Поляков ввели представление о возможном существовании сверхтяжелых монополей с массой Мх ~ 1018 + 1016 ГэВ. Такие сверхтяжелые монополи не могут быть получены на ускорителях. Сделано предположение, что они могли образоваться в ранней Вселенной. Они были введены в GUT-модель и получили название GUT-монополей (рис. 109). Эти монополи имеют сложную структуру и могут служить катализаторами распада нуклона.
    GUT-монополь имеет, помимо магнитного заряда, связанного с электрическим зарядом, еще и цветной магнитный заряд который экранируется на расстояниях ~ 1 фм. Сверхтяжелый монополь вызывает несохранение барионного заряда (т.е. распад протона) М + р → М + е+ + π0. Сечение этого процесса а сравнимо с сечением сильного взаимодействия σ ≈ 10-26 см2. Структура GUT -монополя такова, что, благодаря ненарушенной симметрии в центральной области, он может служить катализатором распада протона (рис. 110).


Рис. 59. Схема распада протона под действием GUT-монополя.

    Его масса mM ≈ МX/αe ~ 1017 ГэВ, где МX ~ 1015 ГэВ − масса векторного бозона, связанного с масштабом нарушения симметрии. Ненарушенная симметрия существовала в момент Большого Взрыва; все взаимодействия имели одну константу  (GUT-модель).

 

 

16.3.1 Поиски монополей

1. Поиск монополей по величине ионизации вдоль следа монополя.

     Магнитный заряд g = n·(137/2)·e = n·68.5·е; g2/(ћc) ~ 34 3 >> 1.
    Около монополя существует связанное электромагнитное поле. Монополь ионизует вещество за счет этого электромагнитного поля. Если он движется со скоростью v, то

где с − скорость электромагнитного поля (скорость света). (g/e)2 = (68.5)2 = 4692, т.е. монополь ионизует в 4692 раза значительнее, чем частица с однократным электрическим зарядом (как ядро с Z = 68.1). Кроме того, ионизация не зависит от скорости монополя, т.к. определяется скоростью света с, т.е. ионизация постоянна вдоль следа частицы. У электрона ионизация а т.к. dE/dx ~ Е2, Е ~ (g/b2)(v/c), то у монополя потери энергии на ионизацию dE/dx ~ (g/b)2·(v/c)2·(1/v2) ~1/c2 ~ const.

    В фотоэмульсии след монополя мог бы существенно отличаться от следа ядра (рис. 111). Это связано с процессом захвата электронов ядром и уменьшением ионизующей способности ядра к концу его следа.

след монополя
след ядра

Рис. 60: Предполагаемые следы монополя и ядра в фотоэмульсии.

Рис. 112. Одна из возможностей рождения монополь-антимонопольных пар.

    Помимо фотоэмульсии для поиска монополей используется метод травления, который позволяет определить след монополя после его прохождения через пластическое вещество.
    Предполагается, что монополи абсолютно стабильны и могут рождаться, например, в процессе е+е- → М (рис.112)

 

 

2. Поиск сверхтяжелых монополей с использованием техники времени пролета.

    Такие монополи скорее всего нерелятивистские и имеют скорость v/c ~10-2−10-4, которую можно измерить в пределах установки.

3. Поиск монополей по наведенному электрическому току в витке проволоки (эксперимент Кабреры, идея Альвареца, рис. 113).


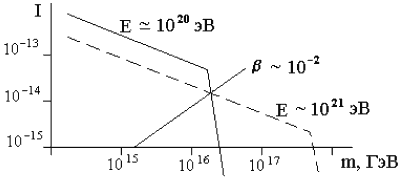
Рис. 113. Схематическое изображение эксперимента Кабреры.

    Когда монополь проходит сквозь виток проволоки, в нем индуцируется электрический ток J, который может быть измерен. В отсутствие монополя ток J = 0, после прохождения монополя через виток будет зарегистрирован скачок тока. В 1982 году Кабрера зарегистрировал подобный сигнал.

    К настоящему времени получены только ограничения на потоки монополей (рис. 114):

I < 10-15 см-2 с-1 ср-1, β = 1.

    Астрофизические ограничения на поток сверхтяжелых монополей:

 I < 10-20 см-2 с-1 ср-1.


Рис. 114: Модельные ограничения на потоки монополей в зависимости от их массы.

16.4 Тахионы

    Тахионы − так принято называть частицы, которые имеют скорость v больше скорости света: v > с.
    Посмотрим, как отразится в формулах такое утверждение.
Е = mc2/(1−β2)1/2, β = v/c > 1, если v > с, то (1−β2)1/2 − мнимая величина. Чтобы измеряемая на опыте величина Е была действительной, полагают, что масса μ√(-1) = μi. Тогда Е = μc2/(β2−1)1/2 будет действительной величиной, т.к. β > 1.


Рис. 115. Распределение по mij2, полученное при обработке событий множественного рождения частиц в рр-соударсниях высокой энергии: mij2 − квадрат эффективной массы любых двух частиц i, j, родившихся в результате соударения.

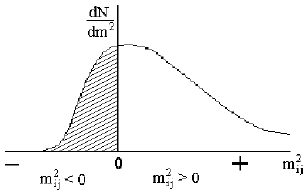
    Используя соотношение Е2 − р2с2 = m2c4  можно определить m2. Если v > с, то рс > Е и m2 < 0. На рис. 115 показано распределение m2, получающееся во многих экспериментах. При соударении протона с протоном рождается много вторичных частиц: р + р = с1 + c2 + ... + сi + сп. Для определения квадрата массы системы двух частиц ij используется формула mij2c4 = (∑Eij)2 + (∑pij)2с2 . Определение энергии каждой из частиц и импульса обычно включает некоторую неточность: Е = Е ± ΔЕ и р = р ± Δр. Неточности ΔЕ и Δр могут быть таковы, что вычисленные значение mij2 могут быть меньше нуля. На рисунке заштрихована область, в которой mij2 < 0. Казалось бы, это свидетельствует о рождении тахионов в результате соударения частиц высоких энергий. Однако детальный анализ показывает, что это может быть следствием погрешности в определении энергии Ei, Ej и импульсов pi, pj.
    Можно отметить следующие особенности в поведении тахионов.

  1. С ростом скорости тахиона его энергия падает, поскольку р2с2 становится больше Е2.
  2. У обычных частиц Е > рс, а у тахионов Е < рс.
  3. Меняется последовательность процессов. Один наблюдатель будет видеть сначала поглощение, а затем − испускание; другой − наоборот.

    Поиски тахионов дают пока отрицательный результат.

16.5 Аксионы

    Аксионы введены в рассмотрение в моделях, связанных с нарушениями СР-симметрии в сильных взаимодействиях. Возникающий при таком нарушении голдстоуновский бозон называется аксионом. Он есть следствие существования дополнительного поля − поля аксиона, появление которого подобно появлению поля Хиггса. В GUT-моделях рассматриваются аксионы безмассовые и массивные. Нижний предел для масс аксионов, получающихся из различных астрофизических оценок, составляет 10-3÷10-5 эВ. Поиск аксионов ведется в лабораторных условиях в различных взаимодействиях их с фотонами или атомарными электронами. Если аксион является массивной частицей, то его можно рассматривать в качестве кандидата в частицы темной материи. До настоящего времени не найдено никаких признаков существования аксионов.

16.6 WIMP-частицы

    Гипотеза о существовании слабовзаимодействующих массивных частиц (Weak Interaction Massive Particle − WIMP-частица) также возникла в связи с проблемой темной материи, которая является крайне интересной астрофизической проблемой. В настоящее время предложено много проектов по поиску таких частиц.
    В апреле 2003 года в Великобритании в бывших соляных копях Северного Йоркшира на глубине 1 км открылась новая подземная лаборатория Boulby Underground (постройка лаборатории стоила 31 миллион фунтов стерлингов). В лаборатории будут проводиться эксперименты по поиску WIMP-частиц.
    Будут работать три эксперимента для регистрации темной материи:

  • NAIAD (Na I Advanced Array Detector);
  • ZEPLIN (с использованием ZonEd с пропорциональным сцинтиллятором в жидком Noble газе, в данном случае с жидким ксеноном):
  • DRIFT (Directional Recoil Indentification From Tracks) − первый эксперимент, в котором помимо регистрации WIMPs будет также определяться направление их прихода.

    Существенные результаты достигнуты в эксперименте DAMA, который претендует на регистрацию WIMP-частиц.
    В состав темной материи могут быть включены экзотические частицы: монополи, тахионы, Хиггс-бозоны, а также массивные нейтрино.

Литература

  1. Клапдор-Клайнгротхаус Г.В., Цюбер К. Астрофизика элементарных частиц. -М.: Редакция журнала УФН, 2000.
  2. PHYSICS LETTERS В. Review of Particle Physics, v. 592, iss. 1-4, 15 July 2004.
  3. Окунь Л.Б. Введение в физику элементарных частиц. -М.: Наука, 1988.

previous home next

На головную страницу

Рейтинг@Mail.ru