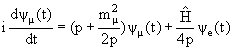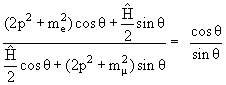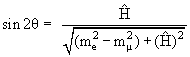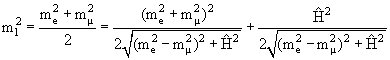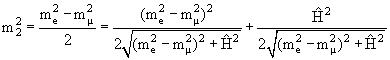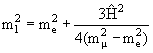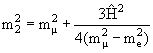Е.В.Широков

Нейтринные осцилляции

    Нобелевская премия по физике 2015 г. была присуждена А. Мак-Дональду и Т. Каджите «за открытие нейтринных осцилляций, демонстрирующих наличие у нейтрино массы» [1]. Чем так важно это явление, о котором говорят уже более полувека?

Артур Мак-Дональд и Такааки Каджита – нобелевские лауреаты 2015 г.

    Нейтринные осцилляции – один из основных вопросов современной физики слабых взаимодействий. Нейтрино – незаряженные лептоны, т.е. частицы Стандартной Модели, не участвующие в сильном взаимодействии, могут быть разделены на три типа (или, как говорят, три аромата), в соответствии с классификацией заряженных лептонов. Это электронные, мюонные и таонные нейтрино. Осцилляциями называются процессы превращения одного типа нейтрино в другое. Несмотря на то, что осцилляции были предсказаны Б.М. Понтекорво ещё в конце 50-х годов прошлого века [2], интерес к ним возник после экспериментов Р. Дэвиса по регистрации солнечных нейтрино, когда был обнаружен так называемый «дефицит солнечных нейтрино». 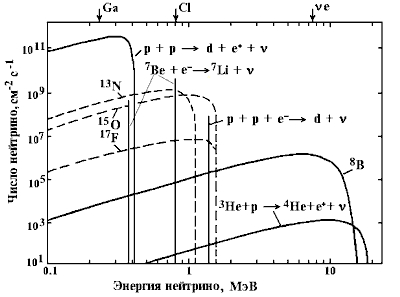Он состоит в том, что нaблюдaемый поток солнечных нейтрино примерно втрое меньше ожидaемого.[3]
    В самом деле, на Солнце, в соответствии со стандартной солнечной моделью, нейтрино в основном возникают в результате реакции протон-протонного цикла (Рис.1):

p + p --->2H + e+ + νe + 0.42 МэВ
(Относительная вероятность такой реакции 99.75%)


Рис.1 Спектр солнечных нейтрино

    Главным источником высокоэнергетичных нейтрино на Солнце служат распады изотопов 8B, которые возникают в реакции 7Be(p,γ)8B (редкой ветви протон - протонного цикла):

8B →  8Be + e+ + νe

    Далее по вероятности образования идут нейтрино СNO – цикла:

13N → 13C + e+ + νe + 1.20 МэВ

15O → 15N + e+ + νe + 1.73 МэВ

    В настоящее время имеется несколько типов экспериментальных данных по регистрации различных групп солнечных нейтрино. В течение 30 лет ведутся радиохимические эксперименты на основе реакции 37Cl + νe → 37Ar + e-. Согласно теории, основной вклад в эту реакцию должны внести нейтрино от распада 8В. Исследования по прямой регистрации нейтрино от распада 8В с измерением энергии нейтрино выполняются с 1987 года. Помимо этого
с 90-х годов прошлого века ведутся радиохимические эксперименты, использующие реакцию «галлий - германий» 71Ga + νe→ 71Ge + e-. Важной особенностью этой реакции является ее чувствительность в основном к первой реакции протон-протонного цикла p + p → 2D + e+ + νe. Темп этой реакции определяет скорость энерговыделения в термоядерной «печи» Солнца в реальном масштабе времени. Во всех экспериментах наблюдается дефицит в потоках солнечных нейтрино по сравнению с предсказаниями стандартной солнечной модели.
    Возможным решением проблемы дефицита солнечных нейтрино и являются нейтринные осцилляции − превращение электронных нейтрино в мюонные и тау-нейтрино. Связь с массой нейтрино заключается как раз в том, что в моделях нейтринных осцилляций изменяющейся (осциллирующей) компонентой является как раз масса нейтрино. Следовательно, если есть осцилляции, есть и ненулевая масса нейтрино.
    Говоря об осцилляциях, нельзя не упомянуть о ряде особенностей в свойствах и классификации этих удивительных частиц. Первое, на что надо обратить внимание, приступая к обсуждению свойств нейтрино, это существование их различных сортов. Как известно, в настоящее время мы определенно можем говорить о трех таких сортах: νe, νμ, ντ и соответственно их антинейтрино. Электронное нейтрино при обмене заряженным W-бозоном переходит в электрон, мюонное - в мюон, таонное – в таон. Это свойство и позволило в свое время установить различие в природе электронного и мюонного нейтрино (Л. Ледерман, 1962 г.)

Возникает основной вопрос − могут ли смешиваться разные сорта нейтрино? При ответе на этот вопрос важно знать, каковы массы нейтрино. Из наблюдений мы знаем, что их массы очень невелики, они существенно меньше, чем массы соответствующих лептонов. Так, для массы электронного нейтрино мы на сегодняшний день (эксперимент KATRIN) [4] имеем ограничение

m (νe) < 1.3 эВ

в то время как масса электрона равна 0.511 МэВ. Во многих случаях для различных оценок, связанных с массами частиц, мы можем полагать массы всех трех нейтрино равными нулю. Если они в точности равны нулю, заметить эффекты возможного смешивания различных сортов нейтрино невозможно. Только если нейтрино имеют отличные от нуля массы, смешивание приобретает физический смысл. Отметим, что нам неизвестны какие-либо принципиальные причины, приводящие к строгому равенству нулю масс нейтрино. Таким образом, вопрос о том, существует ли смешивание разных нейтрино, представляет собой задачу, которую следует решать физическими методами, прежде всего экспериментальными.
    Теперь можно привести некоторые теоретические выкладки, поясняющие ситуацию со смешиванием различных сортов (ароматов) нейтрино. Рассмотрим задачу о двух сортах нейтрино: νe, и νμ,. Для эффектов смешивания следует рассмотреть, как изменяются состояния в зависимости от времени. Эволюцию во времени определяет уравнение Шредингера

(1)

        Здесь H − энергия системы (точнее, оператор энергии). Для состояния с определенной энергией зависимость от времени прямо следует из (1):

|ψ(t)> = eiEt|ψ(t)> (2)

    С этого места мы для простоты изложения используем систему единиц h = c = 1, которая обычно употребляется в физике элементарных частиц. Эта система удобна тем, что в ней имеется всего лишь одна размерная величина, например, энергия. Одинаковые размерности с энергией имеют теперь импульс и масса, а координата x и время t имеют размерность обратной энергии. Применяя это соотношение к рассматриваемому нами случаю нейтрино, когда их массы много меньше импульса, получаем вместо (1):

(3)

         Теперь мы предполагаем, что нейтрино мюонные и электронные могут переходить друг в друга, поэтому волновая функция есть смесь двух состояний

|ν(t)> = ψe(t)|νe> + ψμ(t)|νμ> (4)

Исходя из (4), мы понимаем уравнение (3) как систему уравнений на функции ψe(t), ψμ(t):


 (5)

Для краткости обычно такую систему записывают в виде (3), но понимают тогда ν(t) как столбец из ψe(t), ψμ(t),  а в скобках первый член пропорционален единичной матрице, в то время как величина M2 становится некоторой (2×2)-матрицей с матричными элементами, которые легко получить из системы (6). Здесь очень важна величина Ĥ отличие которой от нуля и приводит к эффектам смешивания. Если ее нет, система распадается на два независимых уравнения и нейтрино, электронное и мюонное, раздельно существуют со своими собственными массами.
    Итак, H ≠ 0. Тогда будем искать решения системы (5) в виде комбинаций

ν1(t) = νe(t)cosθ + νμ(t)sinθ
ν2(t) = −νe(t)sinθ + νμ(t)cosθ		 (6)

которые имеют определенную частоту, то есть имеют вид (2). Для дальнейшего важно отметить, что при малых θ ≈ 0 ν1 является почти чистым электронным нейтрино, а при θ ≈ π/2 − почти полностью мюонным. Складывая первое из уравнений (5), умноженное на cosθ, со вторым, умноженным на sinθ, получаем условие того, что в левой части также содержится только ν1:

(7)

Отсюда имеем определение угла θ, который называется углом смешивания:

(8)

Случай me > mμ, то есть θ ≈ π/4, соответствует максимальному смешиванию. Состояния (6) имеют определенные массы, которые мы получаем из системы (5):


(9)

Знаки в (9) соответствуют случаю mμ > me. Из (9) мы видим, что при нулевом смешивании Ĥ = 0 получаем m1 = me, m2 = mμ. В присутствии смешивания происходит сдвиг масс. Если считать Ĥ очень малым, то


(10)

    Этими соотношениями нельзя пользоваться при равенстве масс, в последнем случае нужно применять точные формулы (9). Важно подчеркнуть, что именно состояния ν1 и ν2 имеют определенные массы и зависят от времени по закону


(11)

    Представим себе, что в начальный момент времени t = 0 родилось электронное нейтрино. Тогда из (6) и (11) получаем зависимость от времени рассматриваемого состояния (общий множитель e-ikt мы опускаем)

(12)

Введем обозначение Δm2 = m12 − m22. Мы видим, что наряду с имевшимся вначале электронным нейтрино здесь появляется и состояние нейтрино мюонного. Вероятность его появления по правилам квантовой механики есть квадрат модуля амплитуды, то есть коэффициента при |νμ>. Она, как видно из (12), зависит от времени и составляет

(13)

где мы измеряем расстояние L в метрах, энергию нейтрино − в мегаэлектронвольтах и разность квадратов масс Δm2 − в электронвольтах в квадрате. Разумеется, мы учитываем малость масс нейтрино, так что L = ct. Мюонная компонента имеет характерную осциллирующую зависимость; это явление получило название осцилляций нейтрино. Что должно наблюдаться как эффект осцилляций нейтрино? Мы знаем, что электронные нейтрино образуют в результате реакции с обменом W электрон, а мюонные − соответственно мюон. Следовательно, пучок, первоначально состоящий из нейтрино электронных, при прохождении его через регистрирующую аппаратуру, генерирует уже не только электроны, но и мюоны с вероятностью, зависящей от расстояния до начальной точки, описываемой формулой (13). Говоря попросту, надо искать рождение “чужих” лептонов.
    Эксперименты по поиску осцилляций нейтрино активно проводятся и, в большинстве случаев, как правило, приводят не к измерению эффекта, а к ограничениям на параметры (13) θ и Δm2.[5]
    Первые попытки ответить на вопрос о наличии осцилляций экспериментальным путём делались ещё в 80-е годы прошлого века. Сейчас нет наверное, ни одного крупного эксперимента, связанного с физикой нейтрино, в котором тем или иным образом не освещалась бы проблема нейтринных осцилляций. Осцилляции нейтрино активно изучались в экспериментах Superkamiokande и SNO, им было уделено немало внимания в самом длительном эксперименте, связанным с солнечными нейтрино − SAGE, проводящемся в Баксанской Нейтринной Обсерватории на Северном Кавказе [6]. Однако в последние 10-15 лет возник целый класс отдельных экспериментов, известный под наименованием Oscillations Industry (осцилляторная индустрия), т.е. класс экспериментов, нацеленных прежде всего на обнаружение нейтринных осцилляций.
    Современную «осцилляторную индустрию» можно разделить на части, связанные, в первую очередь с природой изучаемых нейтрино. Это эксперименты с солнечными нейтрино (Superkamiokande, SNO, Gallex, SAGE, Borexino), атмосферными (MACRO, Soudan2), и реакторными (KamLand, Double CHOOZ). Отдельно стоит сказать о той части экспериментов, которые особенно бурно развиваются в последнее десятилетие − это ускорительные эксперименты вида «long base» (ускорительные эксперименты с длинной базой), в которых нейтрино генерируются протонным ускорителем, а затем измерения проводятся на значительном (вплоть до сотен километров) расстоянии от места их образования. Преимуществами таких экспериментов является прежде всего то, что а) можно чётко представлять содержание нейтрино определённого типа (как правило, мюонных) в первичном пучке б) за счёт длинной базы вероятность осцилляций становится довольно значительной.
    Теперь необходимо сказать немного подробнее о наиболее значительных «long base» экспериментах последнего времени, как законченных, так и продолжающихся.


Рис.2 Общий вид экспериментов MINOS и Noνa

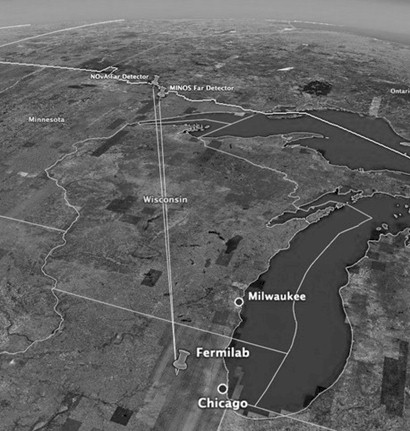
Эксперимент MINOS (Fermilab, США). (Рис.2) В этом проекте использовался относительно низкоэнергетический пучок (3 ГэВ), в нём измерялось время прохождения пучка нейтрино с точностью < 100 нс, сравнивая время регистрации нейтрино в ближнем (ND, 1.1 км) и дальнем детекторах (FD, 735 км). Помимо этого, в эксперименте выполнялось уникальное измерение с целью сравнить энергии нейтрино в заряженных взаимодействиях со временем взаимодействия в дальнем детекторе. Тем не менее, основная цель эксперимента – это изучение осцилляций мюонных нейтрино. Нейтринный пучок, произведённый в Фермилабе, попадал вначале в ближний детектор, расположенный на территории Фермилаба, и потом в дальний детектор (шахта Судан, Миннесота). Сравнивая ароматы нейтрино в дальнем и ближнем детекторах, находились осцилляционные параметры. Результатами измерений 2008-11 г. были следующие значения для разницы масс и угла смешивания: Δm2 = (2.43±0.13)·10-3 эВ2 и sin2(2θ) > 0.90. [7] В настоящий момент эксперимент находится в стадии модернизации для запуска следующего эксперимента с длинной базой − LBNE.


Рис.3 Результаты коллаборации Noνa (август 2015 г.)
(LEM (Library Event Matching) и LID (Likelihood IDentification)-два различных способа отбора событий в эксперименте)

    Большой интерес представляют исследования в «родственном» проекту MINOS проекте Noνa, идущем непосредственно сейчас там же, в Fermilab. Оба проекта имеют схожую географию и так же используют два детектора - ближний и дальний (Рис.2). Однако в проекте Noνa основной задачей является исследование осцилляций νμ→ νe (и аналогичных процессов для антинейтрино), а также исследование иерархии масс нейтрино. 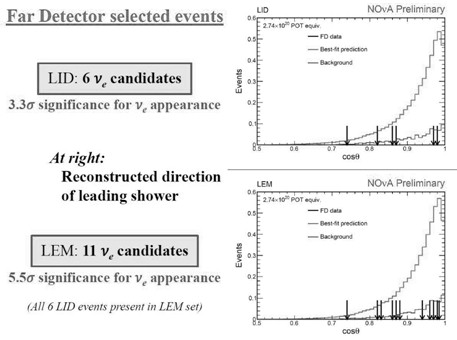Представленные в августе-октябре 2015 г. коллаборацией Noνa результаты (Рис.3), полученные за полтора года, очень хорошо иллюстрируют малость статистики, получаемой в нейтринных экспериментах. [8] Основные осцилляционные параметры, полученные в этом продолжающемся эксперименте равны Δm2 = (2.37±0.16) 10-3 эВ2 и sin2(θ) = 0.51.
    Говоря о современных экспериментах по исследованию осцилляций, невозможно пройти мимо одного из самых известных (если не самом известном) экспериментов – эксперименте OPERA (Гран-Сассо, Италия). Достаточно упомянуть, что в числе коллективов, участвующих в нём – крупнейшие научные центры Европы CERN и INFN (Итальянский Национальный Институт Ядерной Физики). Представлен в данном проекте и Московский Государственный Университет (НИИЯФ имени Д.В.Скобельцына и Физический Факультет).[9]
    Основная цель проекта на длинной базе (732 км.) – прямая регистрация таонов, возникших в результате осцилляций в первичном пучке мюонных нейтрино. Конфигурация детектора представляет из себя эмульсионный детектор для оффлайновых измерений (Рис.4)
    Основная идея обнаружения осцилляций в проекте состоит в следующем - представим, что во время пути пучка мюонных нейтрино от ускорителя в ЦЕРНе до лаборатории Гран-Сассо в результате осцилляций возникла примесь таонных нейтрино. При попадании в детектор нейтрино этого типа с ненулевой (хоть и очень малой) вероятностью, в результате взаимодействия с веществом, могут превратится в своего заряженного партнёра.

Рис. 4 Общий вид детектора OPERA

ντ+ n → τ + p, который затем быстро распадается (10-13 с) по схемам:

τ → μ + ντ + антинейтриноμ
τ → ντ + адроны

    Возникшие при этом частицы (мюон, адроны) оставят треки в эмульсии, которые могут быть обнаружены и расшифрованы. Помимо вышеизложенных процессов возможны и другие каналы взаимодействия, которые в конечном итоге также приводят к образованию различных заряженных частиц. (Рис.5) Технически работа детектора сводится к регулярной замене т.н. эмульсионных «кирпичей» и их тщательном просмотре. Преимущество подобной схемы перед всеми другими заключается в том, что при обнаружении вышеуказанных процессов, это будет являться прямым и явным обнаружением нейтринных осцилляций.
    В заключении необходимо упомянуть о таком интересном эффекте, связанном с нейтринными осцилляциями, как осцилляции нейтрино при взаимодействии с веществом. Выяснение возможностей, возникающих в таком эффекте, связано с работами Л. Вульфенштейна (L.Wolfenstein), С.П. Михеева и А.Ю. Смирнова (так назваемый MSW-эффект). С.П. Михеев, А.Ю. Смирнов и независимо от них американский физики Л. Вульфенштейн показали, что в веществе с плавно изменяющейся плотностью (в частности, на Солнце) может, в принципе, иметь место практически полный резонансный переход электронных нейтрино в мюонные или таонные нейтрино.[10]


Рис.5 Схема регистрации событий в детекторе OPERA

    Этот эффект может возникнуть из-за того, что сечение рассеяния электронных нейтрино на электронах отличается от сечений мюонных или таонных нейтрино. В результате при некоторой плотности вещества может произойти интенсивное взаимопревращение электронного и мюонного нейтрино. Оно должно носить резонансный характер и поэтому идет только для некоторого интервала энергий нейтрино.
    Рассмотрим опять случай двух нейтрино - электронного и мюонного. В веществе имеются протоны и нейтроны в ядрах и электроны. Взаимодействие обоих сортов нейтрино с протонами и нейтронами за счет обмена W и Z происходит одинаково и потому не приводит к новым эффектам по сравнению с распространением в вакууме. Совершенно по-иному обстоит дело с рассеянием нейтрино на электронах. Нейтрино мюонное может взаимодействовать с электроном только за счет обмена нейтральным бозоном Z, в то время как в рассеяние электронного нейтрино (и антинейтрино) на электроне дает вклад и обмен заряженным бозоном W. Действительно, например, W− переходит в лептонную пару e, антинейтриноe, так что процесс рассеяния идет по схеме

антинейтриноe + e → W−→антинейтриноe + e

При рассеянии антинейтрино на электроне происходит слияние их в W, а при рассеянии нейтрино происходит обмен W, при котором исходное нейтрино дает электрон и W+, который поглощается исходным электроном, давая конечное нейтрино. Для мюонного нейтрино такие переходы невозможны.
    Итак, электронное нейтрино имеет дополнительное взаимодействие с электроном, которое описывается дополнительным членом в первой строчке (5):

VW|νe(t)>

Тогда система уравнений, описывающая зависимость волновой функции от времени, изменяется:

(14)

В результате изменяются соотношения между электронной и мюонной компонентами в смесях (6) и значения соответствующих масс, которые получаются из (14). Два значения масс получаются такими:

(15)

где ξ = 2kVW, причем эта величина связана с рассеянием электронного нейтрино на электронах за счет обмена W. Электрослабая теория дает простое выражение

(16)

где GF = (1.16637+0.00002).10-5 ГэВ-2 − известная константа Ферми, характеризующая слабые взаимодействия, а Ne − плотность электронов в веществе. Эта плотность пропорциональна атомному номеру Z элемента и плотности вещества ρ, что и отражено в численной форме соотношения (16). Тогда величину ξ можно представить в виде

ξ = 1.526·10-7Zρk/A эВ2 (17)

(A − атомный вес соответствующего элемента), где плотность ρ выражена в г/см3 и k − в МэВ.
    Согласно системе (14), состояния с массами (15) являются также смесями нейтрино двух сортов, но с другим углом смешивания θm. Его связь с вакуумным углом следует из (14):

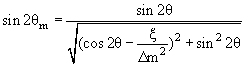(18)

    Рассматривая выражение (15) для масс нейтринных состояний и (18) для угла смешивания в веществе, мы получаем интереснейшее явление резонансной осцилляции нейтрино в веществе. Пусть смешивание нейтрино в вакууме очень мало, то есть sin2θ < 1. Представим себе, что нейтрино с некоторым импульсом k (первоначально электронное) проходит через вещество с переменной плотностью, меняющейся монотонно, например убывающей. Если при этом в каком-то слое плотность ρ = ργ такова, что выполняется равенство:

ξ = 1.526.10-7Zρk/A = Δm2 cos2θ,  

то реализуется резонанс. Действительно, при ρ>ργ, sin2θm<<1 и нейтрино остается электронным. Однако при выполнении равенства (20) sin2θm=1, при дальнейшем уменьшении плотности sin2θm вновь становится малым, но это значит, что 2θm становится близким к π, а θm − к π/2. Из (6) видно, что это соответствует уже почти полностью нейтрино мюонному. Таким образом, при прохождении резонанса происходит смена сорта нейтрино, причем тем полнее, чем меньше вакуумный угол смешивания. Поэтому такая резонансная осцилляция является фактически единственной возможностью проявления малого смешивания нейтрино.
    Явление резонансной осцилляции ярко проявляется также и в зависимости масс нейтрино в веществе от плотности (15). Действительно, начнем с выражения (15) со знаком минус, что в соответствии с уравнениями (15) описывает начальное нейтрино электронное (поскольку содержит характерное для него взаимодействие с электронами VW). Пусть плотность ρ меняется проходя через резонанс. Тогда квадрат массы до резонанса при малом угле θ равен me2 + VW, а после резонанса − mμ2. При прохождении резонанса полностью меняется сорт нейтрино.
    Нужно отметить, что если вместо нейтрино рассмотреть антинейтрино, то основное отличие заключается в знаке члена, описывающего взаимодействие с обменом W. Знаки VW для нейтрино и антинейтрино противоположны. Это означает, что условие резонанса достигается в зависимости от знака Δm2 или только для нейтрино, или только для антинейтрино. Например, если нейтрино мюонное тяжелее электронного, то резонанс может наблюдаться только для начального состояния электронного нейтрино, но не антинейтрино.
    Таким образом, распространение нейтринных (и антинейтринных) пучков в веществе дает богатую физическую информацию. Если основные параметры, то есть Δm2 и θ, известны, то, просвечивая нейтринным пучком некоторый объект, например, планету, звезду и т.д., по составу нейтринного пучка на выходе можно получить картину распределения плотности внутри просвечиваемого объекта.
    Нобелевская премия 2015 г., присуждённая за открытие нейтринных осцилляций, не поставила точку в вопросе об исследовании этого явления, а напротив, обозначила чёткие приоритеты в развитии нейтринной физики, прежде всего, экспериментальной, на ближайшие годы и возможно, даже на более удалённую перспективу.

Литература

  1. http://www.nobelprize.org/nobel_prizes/physics/laureates/2015/
  2. Понтекорво Б.М. ЖЭТФ 33 549 (1957)
  3. Дэвис Р. Мл. Полвека с солнечными нейтрино УФН 174 №4 2004
  4. https://www.katrin.kit.edu/
  5. Куденко Ю.Г. УФН 181 №6 2011
  6. Гаврин В.Н. Солнечные нейтрино в экспериментах SAGE и Borexino Международная сессия-конференция секции ядерной физики ОФН РАН Москва 17-21 ноября 2014 г.
  7. https://www.fnal.gov/pub/science/experiments/intensity/minos.html
  8. R.Patterson. First oscillation result for Nova. Joint Experimental-Theoretical Seminar, Fermilab August 6, 2015
  9. http://www.sinp.msu.ru/ru/post/24343
  10. A.Yu.Smirnov The MSW effect and Solar Neutrinos arXiv:hep-ph/0305106

home

На головную страницу

Рейтинг@Mail.ru