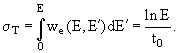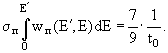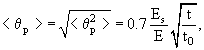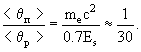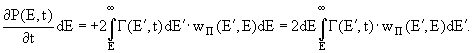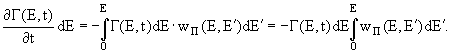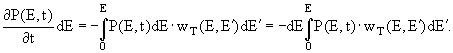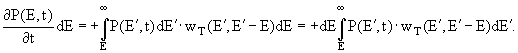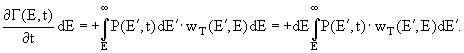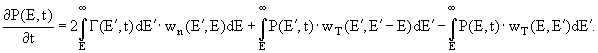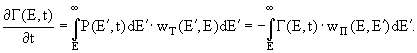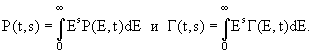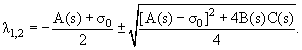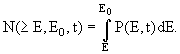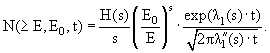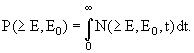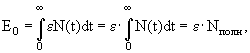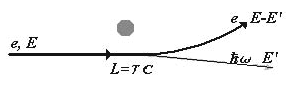4.4. Каскадная теория в приближении А
Рассмотрим сначала простейший вариант теории и определим среднее число частиц в лавине на различных глубинах t ее развития. Пренебрежем всеми процессами взаимодействия, кроме тормозного излучения электронами и рождения пар фотонами (приближение А.). Что кроется за этими условиями?
- 1. Для соответствующих сечений используется приближение полного экранирования, т.е. энергия частицы Е должна быть больше энергии полного экранирования Еп
экр.
- 2. Пренебрегаем ионизационными потерями, т.е. рассматриваем частицы с энергиями, превышающими критическую энергию ε.
- 3. Не учитываются никакие флуктуации.
- 4. Не учитывается комптоновское рассеяние фотонов.
Пусть P(E,t)dE − среднее число электронов с энергией в интервале (E, E+dE) на глубине t, a
Г(E,t)dE − среднее число фотонов в том же интервале энергий и на той же глубине.
Кинетические уравнения в приближении А можно сформировать следующим образом.
Изменение числа частиц в энергетическом интервале (E, E+dE) при прохождении ими слоя dt на глубине t вещества можно записать так:
1. В результате образования пар фотонами с энергией Е' > Е увеличивается число электронов в интересующем нас энергетическом интервале (Е, Е + dE):
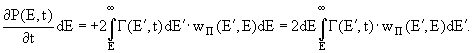
2. В результате образования пар уменьшается число фотонов в энергетическом интервале
(Е, Е+dE):
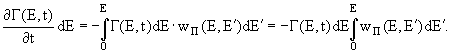
3. В результате тормозного излучения на пути dt уменьшается число электронов в интервале
(Е, Е+dE):
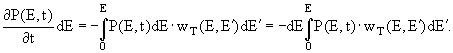
4. В результате тормозного излучения электронов с энергией Е' >Е, часть из них перейдет в интервал энергий (Е, Е+dE}:
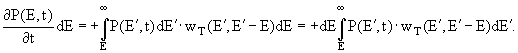
5. Изменение числа фотонов в интервале (Е, Е+dE] из-за тормозного излучения электронов энергии Е' > Е будет:
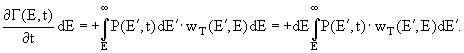
Таким образом, кинетические уравнения каскадной теории можно записать следующим образом:
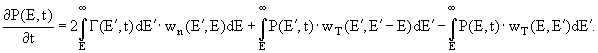
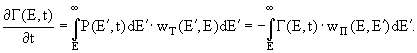
Полученные интегродифференциальные уравнения являются основными уравнениями каскадной теории в области больших энергий. Они линейны относительно функций
P и Г и однородны относительно Е и Е'. Эти свойства уравнений позволяют применить для их решения метод функциональных преобразований Лапласа-Меллина. Для этого перейдем от переменной Е к новой переменной s с помощью соотношений:
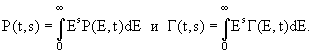
Умножив полученные нами кинетические уравнения на Es и проинтегрировав их по Е от 0 до ∞, получим вместо них другую систему уравнений:
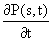 = -A(s)·P(s,t) +
B(s)·Г(s,t), = -A(s)·P(s,t) +
B(s)·Г(s,t),
 = C(s)·P(s,t) − σ0·Г(s,t), = C(s)·P(s,t) − σ0·Г(s,t),
где
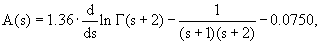
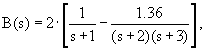
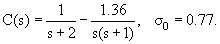
Зависимости A(s), B(s) и C(s) приведены в монографии С.З. Беленького.
Решения вновь полученных уравнений можно записать в виде
P(s,t) = а1exp(λ1t) + a2exp(λ2t),
Г(s,t) = b1exp(λ1t) + b2exp(λ2t),
причем коэффициенты а1, а2, b1 и b2 являются функциями s, a λ1(s) и λ2(s) − корнями квадратного уравнения
λ2 + λ[A(s) + σ0] + A(s)σ0 − B(s)·C(s) = 0;
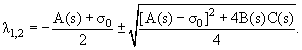
Коэффициенты a1(s), a2(s), b1(s) и b2(s) связаны между собой соотношениями
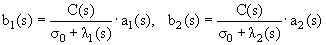
Далее надо сформулировать граничные условия Р(0,Е) и Г(0,Е) и подобрать коэффициенты a1(s)
и a2(s) так, чтобы эти граничные условия были удовлетворены.
Например, если на слой вещества падает один электрон с энергией Е0, не сопровождаемый фотонами, то Р(0,Е) = δ(Е0 − Е), а
Г(0,Е) = 0.
В этом случае
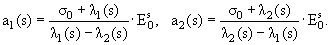
Переходя затем обратно от параметра s к Е получаем искомые функции P(E,t) и
Г(E,t).
Обычно, с практической точки зрения наиболее интересно знать, каково на глубине вещества t полное число электронов (или фотонов) с энергией больше заданной Е при начальной энергии Е0. Иначе говоря, интересен интегральный энергетический спектр лавинных частиц на глубине t:
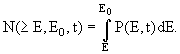
Для частного случая граничных условий, когда при t = 0 имеется один электрон энергии Е0, не сопровождаемый фотонами, число электронов на глубине t с энергией >Е определяется следующим выражением, которое обычно записывается в параметрической форме
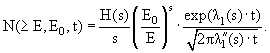
Значения параметров
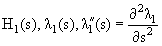
табулированы для разных s в и представлены на рисунке 4.1.
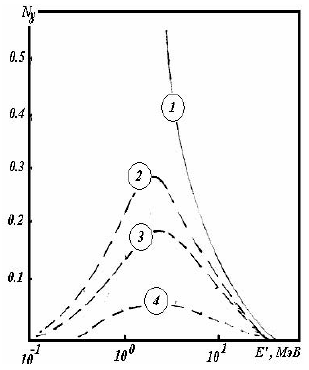
Функция H(s) положительна. Величина ее меняется от 0.55 до 0.2 при изменении параметра s от 0 до 2.
Функция λ1(s) − монотонно убывающая функция параметра s. Она меняет свой знак при s = 1. Для s < 1 эта функция положительна, что приводит к увеличению числа частиц в лавине с возрастанием глубины наблюдения t. При s > 1 функция λ1(s) < 0 и теперь уже она определяет скорость поглощения частиц лавины с глубиной вещества t. Величина ее в интервале изменения s от 1.3 до 1.7 меняется мало: от -0.24 до -0.43.
Функция
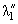 (s) всегда положительна и уменьшается с возрастанием параметра s сначала очень резко (от +75 при s = 0.2 до +2 при s = 0.9), а затем при s > 1 очень медленно. (s) всегда положительна и уменьшается с возрастанием параметра s сначала очень резко (от +75 при s = 0.2 до +2 при s = 0.9), а затем при s > 1 очень медленно.
Параметр s(t), формально введенный при решении кинетических уравнений, имеет глубокий физический смысл: он характеризует степень развития электронно-фотонной лавины. Его часто называют возрастным параметром или просто возрастом ливня. Значение параметра s(t) определяется из уравнения
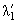 (s)·t + ln(E0/E) = 0, (s)·t + ln(E0/E) = 0,
которое устанавливает связь между глубиной развития лавины t и энергией Е вторичных лавинных частиц. Функция
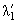 (s) < 0 и возрастает с увеличением параметра s (рис. 4.1). (s) < 0 и возрастает с увеличением параметра s (рис. 4.1).
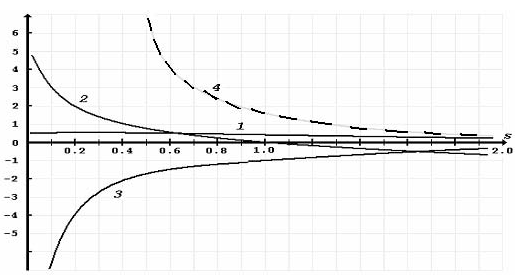
Рис.4.1. Зависимость от возрастного параметра s функций: H(s) − 1, λ1(s) − 2,
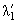 (s) − 3, (s) − 3,
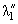 (s) − 4. (s) − 4.
Исследование функции-решения N(> E,E0,t) показывает, что:
- Максимальное число частиц в лавине Nmax(> E,E0t) соответствует s = 1 (по условию экстремума).
- Зная величину s в максимуме, можно найти максимальное число электронов
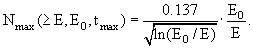
- Глубину максимума лавины можно найти из уравнения
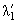 (1)·tmax +
ln (E0/E) = 0, (1)·tmax +
ln (E0/E) = 0,
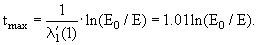
- Величина параметра s(t) меняется с глубиной развития лавины t, поэтому по мере углубления лавины меняется и энергетический спектр вторичных частиц
N(≥ E,E0,t) ~ (E0/E)s
~ E-s.
До максимума, при s < 1, лавина находится в начале своего развития (λ1 > 0), число частиц в ней увеличивается с глубиной, в ней еще много электронов большой энергии - энергетический спектр вторичных электронов "жесткий", "пологий". За максимумом, при s > 1, лавина затухает
(λ1 < 0), спектр становится более "мягкий", более крутой, средняя энергия электронов меньше, чем в максимуме развития каскада.
Наличие максимума в числе лавинных частиц физически совершенно понятно. Сначала идет процесс размножения частиц из-за тормозного излучения электронов и последующего образования фотонами электронно-позитронных пар. Процесс размножения идет до тех пор, пока энергия лавинных частиц в среднем не упадет до выбранного минимального значения энергии Е или до критической энергии ε. При дальнейшем движении частиц в веществе число их будет уменьшаться и образовавшаяся лавина затухать. Аналогичное положение имеет место и для фотонов. Поскольку эффективные сечения для образования пар и испускания тормозного излучения сравнительно близки друг к другу, отношение числа фотонов и электронов в лавине остается приблизительно постоянным.
Из всего рассмотрения ясно, что резко выраженный максимум в числе частиц будет наблюдаться только в случае, если на данное вещество падают частицы с одной и той же энергией Е0. Если же первичные частицы имеют разные энергии (спектр энергий), то максимумы для частиц каждой энергии будут получаться на разных глубинах, и суммарная кривая окажется расплывчатой. При степенном виде спектра первичных частиц суммарная кривая вообще может не иметь максимума.
На больших глубинах, далеко за максимумом, число частиц будет экспоненциально убывать по закону поглощения
exp (λ1(1.8)t) = e-0.47t.
Для ряда экспериментальных задач нужно знать распределение по энергиям электронов всей лавины, т.е.
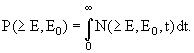
Если Е0 >> Е, то P(>E,E0) ~ Е-1 т.е. совпадает с видом энергетического спектра частиц в максимуме лавины. Поскольку этот спектр получается в результате усреднения спектра лавинных частиц по глубине, то полученный спектр обычно называют
равновесным спектром.
4.5. Каскадная теория в приближении Б
Приведенные ранее рассуждения относились к случаю, когда энергия лавинных частиц Е > ε в легких веществах и Е >Еп экр − в тяжелых. Однако при экспериментальном наблюдении лавины (например, с помощью ионизационных калориметров) регистрируются все частицы, способные создавать ионизацию в детекторе, т.е. практически заряженные частицы любых энергий. Поэтому следующее приближение каскадной теории (приближение Б) должно учитывать ионизационные потери электронов лавины, комптоновское рассеяние фотонов и уменьшение сечения образования ими электронно-позитронных пар с уменьшением энергии.
Учесть ионизационные потери можно введением в кинетическое уравнение для электронов нового дополнительного члена. Этот член должен, с одной стороны, учитывать, что в энергетический интервал (Е, Е+dE] в результате ионизационного торможения на пути dt может войти часть электронов из интервалов с более высокой энергией, и, с другой стороны, часть электронов может покинуть этот интервал по той же причине, Поэтому изменение числа электронов в энергетическом интервале (Е, Е+dE) за счет ионизационного поглощения может быть описано выражением
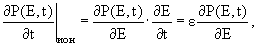
т.к. на пути dt на ионизацию вещества расходуется энергия dE = εdt.
Для фотонов переход к более низким энергиям по сути мало что изменит, если рассматривать каскад в легком веществе (рис.4.2а), т.к. учет комптоновского рассеяния компенсирует падение сечения рождения пар. Поэтому суммарный коэффициент поглощения фотонов в легких веществах остается постоянным вплоть до энергии фотонов
hν ~ 0.1·ε.
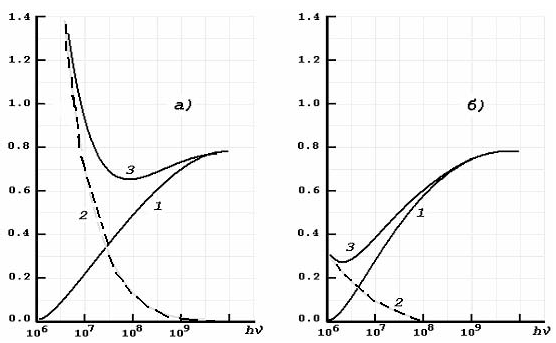
Рис. 4.2. Вероятности: 1− рождения пар, 2 − комптоновского рассеяния, 3 − их сумма на l t0-единице в воздухе (а) и свинце (б)
В тяжелых (рис.4.26) веществах необходимо учитывать сложную зависимость сечения взаимодействия фотонов от их энергии. Это обстоятельство приводит к тому, что приходится решать каскадные уравнения для легких и тяжелых веществ отдельно. Добавление этих членов в полученные ранее уравнения сразу же существенно усложняет задачу. Для решения этих уравнений разработаны специальные методы: метод моментов, метод статистических испытаний и др. Несмотря на возросшую сложность уравнений, решение их приводит к выводу, что общая качественная картина развития каскада в веществе остается прежней: зависимость числа частиц от глубины t также, как и в приближении А, описывается функцией с максимумом. Однако количественные изменения довольно существенны.
В легких веществах глубина максимума лавины tmax и число электронов с энергией Е > 0 в максимуме каскада будут:
tmax = ln(E0/ε), Nmax(≥0,E0,tmax)
= 0.3/ln(E0/ε)·(E0/ε).
Появление в этих выражениях 8 вместо Е понятно, т.к. частицы с энергией
Е < ε не участвуют в дальнейшем развитии каскада, быстро поглощаясь из-за ионизационных потерь.
В тяжелых веществах формулы для tmax и Nmax несколько сложнее:
tmax = k2ln(E0/ε), Nmax
= k1/ln (E0/ε)·(E0/ε),
где параметры k1 и k2 зависят от начальной энергии Ео (таблица 4.2). Таким образом, число частиц в максимуме каскада в тяжелых веществах меньше, а глубина максимума больше, чем в легких веществах, т.е. электронно-фотонная лавина глубже проникает в тяжелые вещества.
Таблица 4.2. Зависимость параметров k1 и k2 от Е0
| Е0, эВ |
k1 |
k2 |
| 5·108 |
0.172 |
1.40 |
| 109 |
0.180 |
1.33 |
| 1010 |
0.200 |
1.29 |
Это происходит из-за того, что в тяжелых веществах энергия полного экранирования существенно меньше, чем в легких веществах. Поэтому суммарный коэффициент поглощения фотонов с энергиями, близкими к ε, в тяжелых веществах существенно меньше, чем для фотонов больших энергий. Следовательно, фотоны таких энергий (~ ε) в тяжелых веществах являются более проникающими, т.к. поглощаются слабее. Фотоны проносят энергию вглубь и затягивают лавину. Кроме того, отношение числа фотонов к числу электронов лавины в тяжелых веществах существенно больше, чем в легких веществах. На рис. 4.3 приведены каскадные кривые в свинце для числа электронов N(> 0,E0,t) в ливне, вызванном первичным электроном энергии Е0.
Энергетический спектр лавинных электронов остается степенным
~ Еs как и в случае приближения А. В максимуме ливня (s = 1) около 80% электронов имеют энергию меньше критической б и около 5% -менее 0.3 ε. Средняя энергия электронов в максимуме каскада близка к 8. Энергетический спектр лавинных электронов за максимумом практически не зависит от Е0. Наклон каскадных кривых в этой области одинаков для разных Е0.
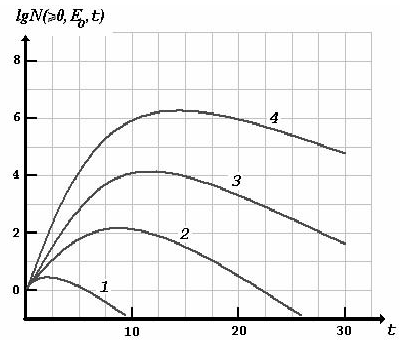
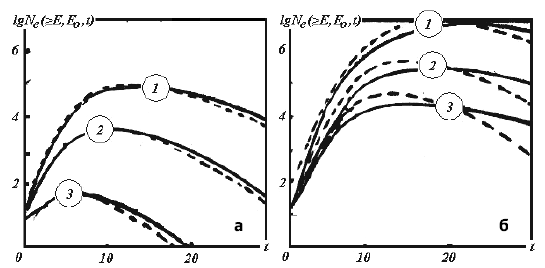
Рис. 4.3. Каскадные кривые в свинце от первичного электрона энергии Е0
(приближение Б)
1 − E0 = 108 эВ, 2 − Е0= 1010 эВ, 3 −
Е0 = 1012 эВ, 4 − Е0 =1014 эВ
Эта часть каскадных кривых может быть аппроксимирована экспонентой е-0.3t, т.е. на пути в 3.3 каскадных единицы число ливневых частиц уменьшается в е раз.
Вся первичная энергия частицы Ео, в конечном счете расходуется на ионизацию, производимую заряженными частицами. Все остальные процессы (радиационное торможение, образование пар, комптон-эффект) лишь переводят энергию от фотонов к электронам и обратно. Поэтому справедливо считать, что теряется энергия ливня только за счет ионизации. Поэтому должно выполняться соотношение (закон сохранения энергии)
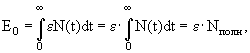
где Nполн − полное число частиц в лавине (площадь под каскадной кривой) определяется величиной Е0/ε.
4.6. Осевое приближение каскадной теории
Как уже ранее обсуждалось, расстояние r, на которое отходит электрон от оси ливня в поперечном направлении, определяется в основном многократным кулоновским рассеянием электронов каскада на пути в 1 t0-единицу. При этом величина угла рассеяния обратно пропорциональна энергии этих электронов:
<θp> = 0.7(Es/E)(t/t0)1/2.
Следовательно, более энергичные частицы каскада испытывают меньшее кулоновское рассеяние и, вследствие этого, располагаются ближе к оси ливня, т.к.
r = t0 tg<θp> ~· t0<θp>. Если рассматривать лавинные частицы в круге малого радиуса
r << t0, то мы будем иметь дело с частицами очень больших энергий:
r/t0 = <θp> ≈ Es/E.
Например, в круге радиуса r = 100 мкм находятся лавинные частицы с энергией Е > 1 ГэВ. Поскольку эта энергия много больше Еп
экр и ε, то можно ограничиться приближением А каскадной теории и не учитывать ионизационные потери лавинных электронов.
Но в случае приближения A N(>E,E0t) = ƒ(E0/E,t) − есть функция двух переменных E0/E и t. Так как Е = Es/r (если
r измерять в t0-единицах ), то можно принять, что в круге радиуса r
<< t0
N(≥E,E0,t) = ƒ(E0r/E,t).
|
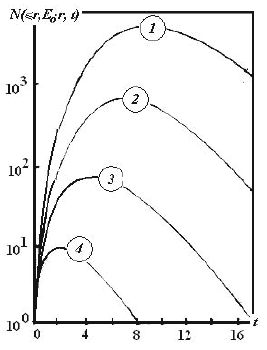
Рис.4.4. Зависимость числа электронов в круге радиуса r от глубины развития каскада t (осевое приближение каскадной теории):
1 − E0r = 107 ГэВ·мкм, 2 − E0r = 106
ГэВ·мкм, 3 − E0r = 105 ГэВ·мкм, 4 − E0r
= 104 ГэВ·мкм |
Таким образом, число частиц в круге радиуса r на глубине каскада t не зависит от энергии этих частиц Е, а зависит от произведения Е0r. Это заключение очень важно, т.к., определяя число частиц в круге радиуса
r на глубине каскада t, можно сразу же найти первичную энергию E0 частицы, вызвавшей этот каскад. Этот метод исследования получил название "метода осевого приближения".
Расчеты каскадных кривых для осевого приближения были впервые выполнены в 1961 г. Пинкау и Нишимурой. Эти кривые устанавливают связь между числом частиц в круге малого радиуса
r и величиной Е0r для разных глубин развития каскада t (рис.4.4). Поскольку речь идет о
r < 1 мм, то для детектирования таких ливней чаще всего используют эмульсионные детекторы − фотоэмульсионные и рентгеноэмульсионные камеры, которые позволяют определить (с помощью микроскопа или фотометрированием) число частиц в круге определенного радиуса.
Границы применимости осевого приближения зависят от параметров ливня, свойств вещества, энергии лавинных электронов Е, глубины наблюдения t и начальной энергии Е0.
Кроме того, поскольку речь идет о малых r, т.е. очень больших энергиях Е, то надо учитывать эффект Ландау - Померанчука - Мигдала, не учтенный в работах Пинкау и Нишимуры.
|