Ядерные реакции
Развитие ядерной физики в большой степени определяется
исследованиями в такой важной ее области, как ядерные реакции. Однако после
того, как Резерфорд впервые наблюдал ядерную реакцию, до появления первой модели
ядерной реакции прошло довольно много лет.  -Частицы от радиоактивных
источников могли эффективно преодолеть кулоновский барьер только на самых легких
ядрах. С появлением ускорителей ситуация радикально изменилась, теперь можно
было бомбардировать ядра не только -Частицы от радиоактивных
источников могли эффективно преодолеть кулоновский барьер только на самых легких
ядрах. С появлением ускорителей ситуация радикально изменилась, теперь можно
было бомбардировать ядра не только  -частицами.
Повысились энергии и интенсивности пучков частиц. -частицами.
Повысились энергии и интенсивности пучков частиц.
Первая модель ядерной реакции появилась в 1935 году, это была
модель Оппенгеймера -
Филлипс,
предложенная для интерпретации реакции (d,p) при низких энергиях.
Дальнейший прогресс представлений о механизмах ядерных
реакций долгое время был связан с концепцией составного ядра (компаунд-ядра),
которая была предложена в 1936 году Н. Бором для объяснения резонансной
структуры сечений захвата нейтронов и протонов низких энергий атомными ядрами.
Ширина этих резонансов была очень небольшой (~0.1 эВ) и они располагались близко
друг к другу. Возникновение таких узких резонансов можно понять, если
предположить, что из-за сильного взаимодействия между нуклонами кинетическая
энергия налетающей частицы быстро перераспределяется между все большим
количеством нуклонов. В результате образуется равновесная система, так
называемое составное-ядро. Из-за того, что энергия в составном ядре
статистически распределена между многими нуклонами вероятность того, что один из
нуклонов будет иметь энергию, достаточную для вылета из ядра мала, а время жизни
такого ядра велико
(10-14 - 10-18 с). Эмиссия из такой системы определяется
константами движения и геометрическими параметрами всего составного ядра как
целого и не зависит от способа его образования (гипотеза независимости Бора),
то есть сечение реакции может быть факторизовано
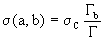 , ,
где σc - сечение образования составного
ядра, Гb - ширина распада составного ядра по каналу b, Г - полная
ширина распада составного ядра.
Первое количественное описание реакции, идущей через
компаунд-ядро, было получено Г. Брейтом
и Е. Вигнером в 1936 году.
Широкое распространение в расчетах сечений ядерных реакций
получила феноменологическая модель испарения, предложенная
В. Вайскопфом
в 1937 году. В 30-50-х годах на основе "первых принципов" развивалась формальная
теория ядерных реакций. Различные варианты формальной теории не содержали
конкретных физических предположений таких, например, как гипотеза независимости,
и в принципе могли описывать различные механизмы ядерных реакций. Однако
применение их для практических расчетов было связано с большими трудностями. Тем
не менее развитые в этих работах подходы позволили глубже понять физику
процессов, происходящих в ядре и были использованы при создании моделей.
К началу 50-х годов создание последовательной теории реакций,
идущих через составное ядро, было в основном завершено. С помощью теории
компаунд-ядра удалось удовлетворительно описать большое количество
экспериментальных данных. При вычислении сечений предполагали, что любая
частица, попав в ядро, должна поглотиться (модель "черного" ядра), т.е.
одночастичное движение должно полностью затухнуть. Однако начали появляться
экспериментальные данные, которые свидетельствовали, что одночастичное движение
не затухает полностью.
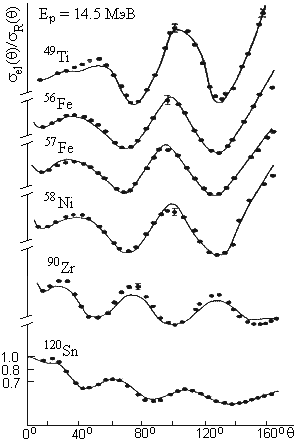
Рис. 9. Экспериментальные данные по упругому рассеянию протонов и результаты
расчетов по оптической модели |
Для описания усредненного поведения сечений
Г. Фешбах,
К. Портер и
В. Вайскопф в 1954
году предложили оптическую модель, которая получила свое название из-за
аналогии рассеяния частиц на ядре с прохождением света через полупрозрачную
сферу. В оптической модели предполагается, что ядро может быть описано
комплексной потенциальной ямой
U(r) = V(r) + iW(r),
где мнимая часть W(r) описывает поглощение частиц падающего пучка.
Успехи оптической модели в описании упругого рассеяния (см.
рис.9) привели к пониманию механизма протекания прямых ядерных реакций, в
принципе отличающегося от механизма протекания ядерных реакций через составное
ядро. Малая величина мнимой части оптического потенциала, полученного из
эксперимента (несколько МэВ) указывает на довольно большую длину свободного
пробега нуклона в ядре. Таким образом, существует заметная вероятность того, что
налетающий нуклон испытает одно взаимодействие с нуклоном ядра мишени, после
чего один из этих нуклонов покинет ядро. Первая модель для описания прямых
механизмов в реакциях (d,p) была предложена в 1950 году
С. Батлером.
Предполагая поверхностный характер реакции, можно с помощью простых
квазиклассических соображений объяснить появление максимумов в угловых
распределениях. Такие максимумы должны появляться при углах, для которых
выполняется условие
l = qR,
где l - переданный ядру орбитальный момент, q - переданный импульс, R -
радиус ядра. В середине 50-х годов для описания прямых механизмов был развит
метод искаженных волн (МИВ), который можно рассматривать как обобщение
оптической модели на неупругие каналы. В МИВ используется то, что в прямых
реакциях налетающая частица передает свою энергию и импульс небольшому числу
степеней свободы ядра. Это позволяет получить приближенное решение
многочастичного уравнения Шредингера, используя теорию возмущения. Полный
гамильтониан системы записывается в виде
H = H0 + Hост,
где H0 - гамильтониан системы из двух частиц, взаимодействие между
которыми описывается оптическим потенциалом Vопт, Hост
- гамильтониан остаточного взаимодействия, который рассматривается как малое
возмущение, переводящее систему в конечное состояние. Процесс ядерной реакции
разбивается на 3 этапа.
- Движение налетающей частицы в "искажающем" (оптическом) потенциале ядра
мишени.
- Передача нуклонов под действием остаточного взаимодействия
- Движение вылетающей частицы в поле конечного ядра.
Модели прямых ядерных реакций использовались в основном
для описания жесткой части энергетических спектров продуктов реакций, которая
связана с возбуждениями изолированных состояний конечных ядер (рис.10).
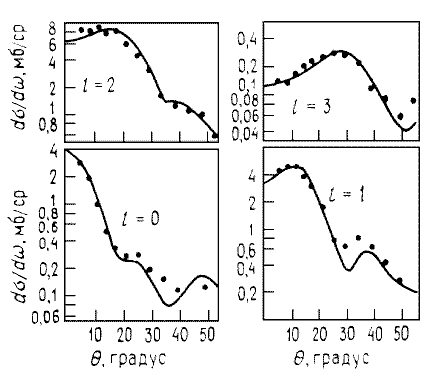 Рис. 10.
Экспериментальные угловые распределения для различных состояний конечного
ядра 59Ni, возбуждаемых в реакции 58Ni(d,p)59Ni
при энергии Ed = 15 МэВ, и результаты расчетов по методу искаженных волн.
Все четыре случая различаются передачей орбитального момента l Рис. 10.
Экспериментальные угловые распределения для различных состояний конечного
ядра 59Ni, возбуждаемых в реакции 58Ni(d,p)59Ni
при энергии Ed = 15 МэВ, и результаты расчетов по методу искаженных волн.
Все четыре случая различаются передачей орбитального момента l |
Модели, использующие концепцию составного ядра
претендовали на описание непрерывного спектра. Действительно, в спектрах
вылетающих частиц при энергиях ускоряемых ионов, достижимых в обычных
циклотронах, непосредственно за областью дискретных пиков начиналось характерное
для процесса испарения непрерывное распределение. Однако по мере увеличения
энергий ускоряемых ионов, в основном связанном со строительством изохронных
циклотронов (Развитие ускорительной техники происходило так, что
от циклотронов, ускоряющих, например, протоны до энергий ~10 Мэв сразу
перешли к ускорителям на сотни МэВ. Область десятков МэВ долгое время была слабо
исследована.), увеличивалась область между пиками, связанными с
возбуждением дискретных состояний конечных ядер, и испарительным распределением
(см. рис.11), которую не могли адекватно описать существующие модели.
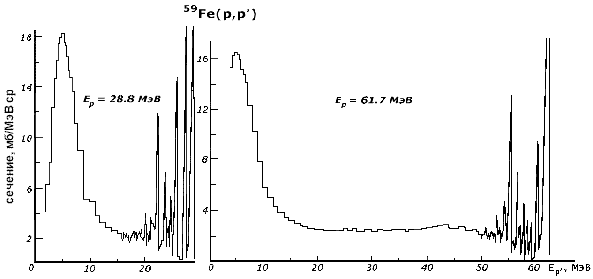 Рис. 11. Спектры
протонов из реакции 59Fe (p,p'), измеренные под углом 300
в л.с. при энергиях протонов 28.8 и 61.7 МэВ |
Высказывалось предположение, что эта область спектра формируется в результате
процессов происходящих во время движения составной системы к равновесному
состоянию - составному ядру. После появления в 1966 году пионерской работы Дж. Гриффина
наметился экспоненциальный рост экспериментальных и теоретических работ,
посвященных так называемым предравновесным процессам. Сегодня предравновесные
процессы делят на два класса: многоступенчатые прямые процессы, в которых
происходит эволюция открытых состояний, и многоступенчатые компаунд-процессы,
связанные с эволюцией закрытых состояний и связи их с открытыми состояниями. Под
открытыми состояниями понимаются состояния, в которых хотя бы один нуклон
находится выше энергии связи и может вылететь. В закрытых состояниях все нуклоны
находятся ниже энергии связи.
В реакциях с тяжелыми ионами в 70-е годы в Дубне группой
В. Волкова был открыт новый тип ядерных реакций - реакции глубоконеупругих
передач. Специфика глубоконеупругих передач обусловлена качественными
изменениями процесса взаимодействия двух сложных ядер по сравнению с реакциями с
легкими ионами. В основе этого взаимодействия лежат процессы формирования,
эволюции и распада специфического ядерного комплекса - двойной ядерной системы.
За счет кинетической энергии сталкивающиеся ядра проникают друг в друга,
возрастает зона перекрытия их поверхностей. Из-за большой вязкости ядерной
материи и соответственно из-за большого ядерного трения подавляющая часть
кинетической энергии переходит в возбуждение системы, скорость относительного
движения падает до нуля. Часть кинетической энергии переходит в энергию вращения
ядер. Однако несмотря на интенсивное взаимодействие, оболочечная структура
обеспечивает ядрам сохранение их индивидуальности. В зоне обмена нуклоны
переходят из одного ядра в другое, однако нуклоны внутренних оболочек образуют
довольно устойчивые коры, сохраняющие индивидуальность ядер. Эволюция системы
происходит в направлении минимума потенциальной энергии системы, в процессе
которой нуклоны от одного ядра оболочка за оболочкой передаются другому. Если
кулоновские и центробежные силы превосходят силы притяжения, система будет
распадаться. Однако, если результирующая сила невелика, распад будет происходить
медленно и от ядра к ядру может быть передано значительное количество нуклонов.
Более глубокое понимание механизма взаимодействия двух сложных ядер помогает в
поиске оптимальных способов синтеза экзотических и сверхтяжелых ядер.
|
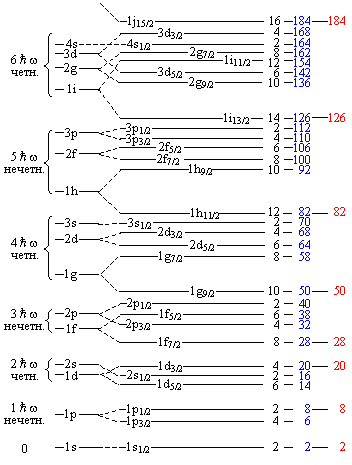
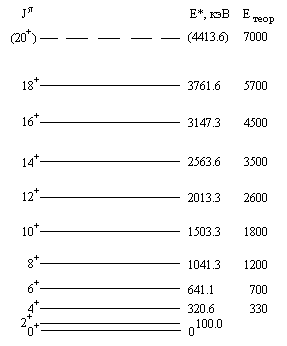
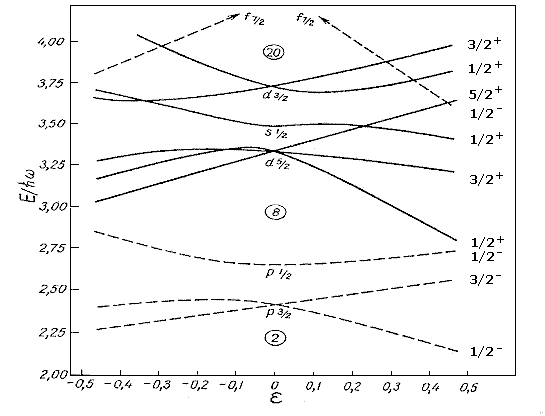 Рис. 8.
Одночастичные уровни энергии в потенциале Нильссона
Рис. 8.
Одночастичные уровни энергии в потенциале Нильссона
 Рис. 10.
Экспериментальные угловые распределения для различных состояний конечного
ядра 59Ni, возбуждаемых в реакции 58Ni(d,p)59Ni
при энергии Ed = 15 МэВ, и результаты расчетов по методу искаженных волн.
Все четыре случая различаются передачей орбитального момента l
Рис. 10.
Экспериментальные угловые распределения для различных состояний конечного
ядра 59Ni, возбуждаемых в реакции 58Ni(d,p)59Ni
при энергии Ed = 15 МэВ, и результаты расчетов по методу искаженных волн.
Все четыре случая различаются передачей орбитального момента l