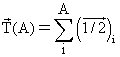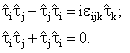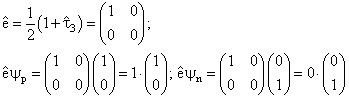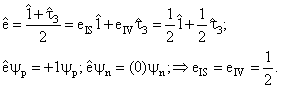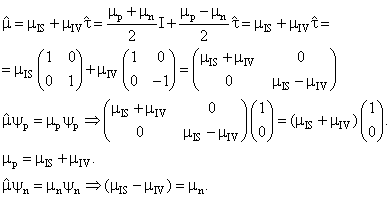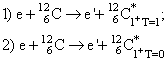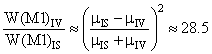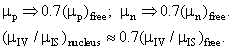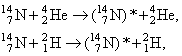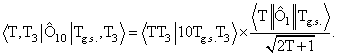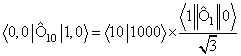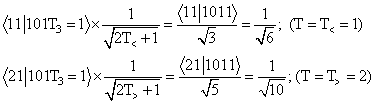Н.Г. Гончарова ИЗОСПИН     Изоспин – одна из основных характеристик адронов, т.е. частиц и ядер, участвующих в сильных взаимодействиях.     В таблицах частиц (см., например.[1]) эта характеристика обозначается как I и занимает первое место в строке характеристик адронов: IG(JPC).     Изоспин – вектор; в таблицах указывают значение его модуля. Часто указывают значение его проекции I3 (или Iz) на выделенную ось в пространстве изоспина. (В литературе по физике ядра изоспин и его проекция обычно обозначаются символами T и T3 ).     Изоспин является также одной из характеристик фундаментальных фермионов – кварков (барионный заряд кварков В=1/2).     Для всех кварков спин и четность JP =1/2+. Квантовое число Flavor (тип кварка) u d c s t b I 1/2 1/2 0 0 0 0 I3 +1/2 -1/2 0 0 0 0 c (Charm) 0 0 +1 0 0 0 s (Strangeness) 0 0 0 -1 0 0 t (Topness) 0 0 0 0 +1 0 b (Bottomness) 0 0 0 0 0 -1     Антикварки имеют то же значение спина и изоспина, что и кварки. Все другие квантовые числа антикварков равны по абсолютной величине и противоположны по знаку квантовым числам кварков.     Изоспин и проекция изоспина отличают кварки “первого поколения” от остальных 4 кварков.     Адроны, построенные из кварков «второго», а тем более «третьего» поколения, могут быть обнаружены экспериментально лишь при высоких энергиях столкновения.     Изоспин и его проекция были введены в список важных характеристик объектов микромира при исследовании свойств атомных ядер. (Термин «изоспин» установился не сразу. В литературе 50-80 годов 20 века использовался вначале термин «изотопический», а позже – «изобарический» спин)     Нуклоны представляют собой кварковые системы, состоящие из кварков первого поколения. Кваркам первого поколения, т.е. кваркам u и d , приписывается изоспин I=1/2, причем u кварк имеет значение проекции изоспина + 1/2, а d кварк имеет I3= -1/2. Изоспин антикварка равен изоспину кварка, но проекция изоспина антикварка противоположна по знаку проекции изоспина кварка.     Изоспины адронов являются результатом векторного сложения изоспинов составляющих их кварков.     Величина изоспина адрона указывает на то, сколько у него разных зарядовых состояний. С точки зрения сильных взаимодействий протон и нейтрон являются двумя разными состояниями нуклона с изоспином I=1/2. Вектор может иметь две проекции, которые соответствует протону (uud) и нейтрону (udd) . Из сложения проекций кварков получим значения проекций изоспина протона и нейтрона: I3 (p) = +1/2 и I3 (n) = -1/2.     Проекция изоспина адрона, его заряд и другие квантовые числа связаны правилом (см. [2]): Q = I3 + Y/2, где Y = B + S – гиперзаряд (В – барионный заряд, S – странность).     Число разных зарядовых состояний N соответствует числу проекций N = 2I + 1 изоспина на выделенную ось в изоспиновом пространстве. Для нуклонов N = 2. Частицы или системы частиц, имеющие одинаковый изоспин и разные проекции изоспина, составляют изоспиновые мультиплеты (дублеты, триплеты, и т.д.). Особенностью членов такого мультиплета является то, что они одинаковым образом участвуют в сильном взаимодействии.     Кварки первого поколения могут образовать барионы с изоспинами 1/2 и 3/2. Изоспин 3/2 имеют барионы, которые называются D-изобарами.     Наиболее легкие из мезонов существуют в трех зарядовых состояниях π–, π0 и π+. Изоспин π-мезонов равен I = 1, число членов изоспинового мультиплета N = 2I+1 =3. Значения проекции изоспина -1, 0, +1 соответствуют трем зарядовым состояниям π мезонов (изоспиновый триплет). Если частица не имеет «изоспинового партнера», ее изоспин 0 (изоспиновый синглет). Такой частицей является, например, η-мезон. Λ-гиперон, имеющий кварковую структуру (uds), также является изоспиновым синглетом. Σ-гипероны существуют в трех зарядовых состояниях, изоспин Σ поэтому равен 1, а число проекций единицы равно 3 (-1, 0, +1), как и в случае π мезонов, т.е. это изоспиновый триплет.     (Исторически введение в физику частиц понятия изоспина и его проекции в 60-х годах XX века явилось толчком к появлению гипотезы кварков. Возникновению этой идеи очень помог тот факт, что все открытые к тому времени барионы и мезоны можно было замечательно симметричным образом разместить на схемах, где осью абсцисс было значение проекции изоспина частицы, а на оси ординат – странность.     Поскольку эти схемы состояли из восьми частиц, М. Гелл-Манн, увлекавшийся буддизмом, назвал их «восьмеричным путем».) Рис.1.1. Октет барионов (В = 1, JP =1/2+). Рис.1.2. Октет псевдоскалярных мезонов (В = 0, JP = 0-).     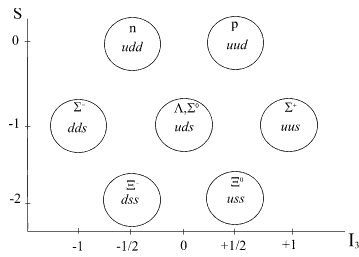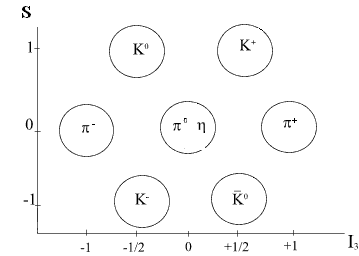«Восьмерки» барионов, по гипотезе М.Гелл-Мана, являются частицами, сконструированными из всего трех составляющих – частиц со спином ½ и барионным зарядом 1/3, причем две из них (u,d) обладают квантовым числом изоспин и двумя возможными его проекциями +1/2 и –1/2 . Третья частица не имеет изоспина, но обладает новым квантовым числом s -«странность». 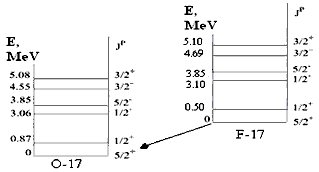Эти составляющие адроны частицы были названы им «кварками».     Восьмерки мезонов представляют собой конструкции из кварков и антикварков. Помимо конструкций барионов и псевдоскалярных мезонов (рис.1.1 и 1.2) в этой схеме получило простое объяснение существование т.н. «векторных» мезонов с JP = 1-, их расположение на графике полностью соответствует рис.1.2. Изоспин в физике ядра     Поскольку в литературе по физике ядра изоспин и его проекция обозначаются обычно символами Т и T3 , в дальнейшем изложении будет использоваться эта традиционная для ядерщиков система обозначений. 1. Зеркальные ядра     Каждое атомное ядро имеет свой неповторимый спектр возбужденных состояний. (Как и атомы разных химических элементов). Экспериментальное исследование этих спектров показало, что у некоторых ядер спектры почти одинаковы в области сравнительно невысоких энергий возбуждения. Эти ядра имели одинаковое количество нуклонов А, причем числа протонов Z одного ядра равнялись числу нейтронов N другого ядра этой пары. Эти ядра получили наименование «зеркальные» ядра /mirror nuclei/. На рис. 2 показаны несколько пар «зеркальных ядер» Рис.2. «Зеркальные ядра»     Для всех известных пар таких ядер имеет место подобие спектров низших возбужденных состояний: спины и четности низших состояний одинаковы, а энергии возбуждения близки.     Ядро как система Z протонов и N нейтронов имеет проекцию изоспина T3 = Z(+1/2) + N(-1/2) = (Z – N)/2, (1.1)     Изоспин системы нуклонов является векторной суммой изоспинов составляющих: (1.2)     Идентичность спектров зеркальных ядер есть проявление протон-нейтронной симметрии, или, другими словами, того факта, что сильные взаимодействия в этих ядрах идентичны. Подобие свойств пар «зеркальных» ядер наблюдается не только в случаях, когда ядра отличаются одним протоном и одним нейтроном (как на ядрах рис.2). Исследование пар ядер с одинаковым числом нуклонов, но отличающихся несколькими протонами, показали близость свойств таких ядер [3].     Близкое подобие спектров зеркальных ядер нарушается кулоновскими силами, которые различны в зеркальных ядрах вследствие разного числа протонов. Схожесть спектров зеркальных ядер показала, что ядерные (т.е. сильные) взаимодействия не зависят от проекции изоспина, или, точнее, сильные взаимодействия инвариантны относительно вращений в изоспиновом пространстве. (Пространство изоспина не совпадает с обычным координатным пространством.)     Однако от величины изоспина ядерные силы зависят! Низшим по энергии состояниям системы нуклонов, т.е. основным состоянием ядра, является состояние с низшим возможным значением изоспина, которое равно (1.3)     Возбужденные состояния ядер могут иметь более высокие значения изоспина, но с той же проекцией. Таким образом, характеристиками уровней данного ядра являются энергия, спин состояния, четность состояния и изоспин. Обычно три последних квантовых числа указываются как JP, T. (Замечание: Поскольку для большинства ядер число нейтронов больше числа протонов, проекция изоспина всех таких ядер по формуле(1.1) – отрицательное число. Чтобы избежать этого неудобства, в статьях по физике ядер часто проекцию изоспина нейтрона считают равной +1/2, а протона -1/2. Тогда T3 = Z(-1/2) + N(+1/2) = (N – Z)/2. В силу независимости сильных взаимодействий от знака проекции изоспина, эта перестановка не меняет физических результатов ядерных исследований.) 2. Роль изоспина в структуре состояний атомных ядер     Зависимость энергии ядерных состояний от изоспина учтена в модели заряженной жидкой капли (формула Вайцзеккера) путем введения «энергии симметрии» (см.[2]): . (2.1)     Ядерные силы инвариантны относительно вращений в пространстве изоспина, поэтому полный ядерный потенциал для ядра А должен иметь вид, обеспечивающий эту инвариантность:  (2.2)     Здесь второй член содержит оператор спина нуклона и оператор спина остаточного ядра. Наличие зависящего от изоспина члена в ядерном потенциале приводит к изоспиновой зависимости положения возбужденного состояния ядра на оси энергий. Оператор поглощения ядром реального или виртуального фотона может быть как изоскалярным, так и изовекторным. Соответствующие этим двум возможностям операторы возбуждения будут, соответственно, скалярами (ΔT = 0) или векторами (ΔT = 1) в пространстве изоспина. Вследствие зависимости ядерных сил от изоспина, возбужденные состояния с изоспином T0, равным изоспину основного состояния ядра, расположены (в среднем) ниже по энергии возбуждения, чем состояния с T0+1 (изоспиновое расщепление уровней). (2.3)     (Оценки величины V1 весьма приближенны: от V1 ≈ 100 МэВ [4] до V1 ≈ 60 МэВ [5].     При изовекторном возбуждении ядра (Z,A) с изоспином основного состояния, не равным 0 , возникают две изоспиновые ветви возбужденных состояний: (2.4)     Возбуждение ветви c T=T0-1 в данном ядре невозможно, поскольку это значение изоспина не может иметь то значение проекции (1.1), которое определяется числом протонов и нейтронов ядра./ 3. 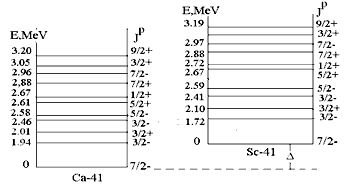Изобар-аналоговые состояния (ИАС)     Ядра с одинаковым количеством нуклонов А, но разными числами протонов и нейтронов, имеют различные спектры возбуждений. Но в их спектрах присутствуют т.н. изобар-аналоговые состояния. На рис. 3.1 показаны спектры двух таких ядер-изобар, отличающихся изоспином. В спектре ядра с изоспином основного состояния T= T0 при более высоких энергиях будут находиться уровни возбужденных состояний с изоспином T=T0+1. 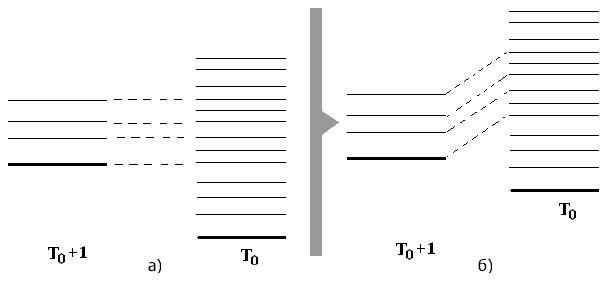Если бы в ядрах отсутствовало электромагнитное взаимодействие, энергии таких состояний с одинаковыми значениями изоспина T=T0+1 были бы одинаковыми (рис.3а). Электромагнитное отталкивание протонов повышает энергию уровней ядер (рис.3б).     Изобар-аналоговые состояния (ИАС) в спектрах средних ядер были обнаружены в 1961 г [6].     Ядро с A=(Z+1)+(N-1) за счет энергии симметрии имеет более низкое значение энергии основного состояния. «Включение» кулоновского взаимодействия протонов повышает энергии уровней ядра с A=(Z+1)+(N-1) (рис.3б). Пунктирными линиями на рис.3 соединены уровни в спектрах этих ядер, имеющие одинаковые значения изоспина, т.е. изобар-аналоговые состояния. Рис.3.Схемы уровней двух ядер-изобар. а) – без учета кулоновского взаимодействия; б) – кулоновское взаимодействие включено. Пунктиром соединены изобар-аналоговые уровни.     Волновые функции изобар-аналоговых состояний идентичны по отношению к сильным взаимодействиям. Структура этих функций отличается только заменой протона на нейтрон в том же квантовом состоянии. Рис.3.2. Схема уровней ядер с А=14. Изобар-аналоговые состояния имеют JP = 0+,T = 1 4. Формализм квантовой механики изоспина     Изоспин – квантовый вектор, являющийся характеристикой не только нуклонов и ядер, но и любых адронов. Оператор квадрата изоспина является собственным оператором волновой функции адрона или системы адронов: (4.1)     Квантовая физика изоспина построена по образцу квантовой физики спина. (Основой аналогии является существование двух значений проекции спина нуклона и двух значений проекции его изоспина).     В изоспиновом пространстве действуют операторы, совпадающие по матричной форме с операторами Паули: (4.2)     Для них справедливы соотношения: (4.3)     Функция, описывающая состояние нуклона в пространстве изоспина, может быть представлена в виде двурядной матрицы: (4.4)     Этот формализм позволяет получить правильные значения для зарядов протона(+1) и нейтрона (0) в единицах е:     Оператор заряда нуклона можно представить как  (4.5)     Оператор заряда в пространстве изоспина (4), является суммой изоскалярного и изовекторного операторов. Это же соотношение позволяет найти вклады этих операторов в функцию возбуждения:  (4.6)     Аналогичным образом можно представить оператор магнитного момента нуклона как сумму изоскалярного и изовекторного операторов: (4.7)     Значения магнитных моментов свободных протона и нейтрона ( в величинах ядерного магнетона eћ/2mpc) известны из эксперимента: μp = 2×2.793;   μn = 2×(-1.913).     Отсюда следует, что (4.8) Это соотношение изовекторного и изоскалярного магнитных моментов объясняло, в частности, отношение вероятностей возбуждения ядерных состояний ядер в реакциях неупругого рассеяния электронов (e,e’). Например, вероятность реакции 1 в (4.9) много выше, чем реакции 2, хотя энергии возбужденных уровней с JP=1+ Т=0 ниже, чем уровня с Т=1 и Е=15.1 MeV, который возбуждается в первой реакции:  (4.9)     Из отношения изовекторного и изоскалярного магнитных моментов (3.8) следует, что в т.н. магнитных возбуждениях, например, М1, вероятность изовекторного возбуждения должна превышать вероятность изоскалярного почти в 30 раз, (4.10)     Реальное превышение вероятностей около 15! Поэтому в практических расчетах изоспиновых коэффициентов в реакциях возбуждения ядер вводят фактор «подавления» (обычно 0.7) магнитных моментов нуклонов ядра за счет взаимодействия «свободных» магнитных моментов с ядерной средой: (4.11) 5. Изоспин в ядерных реакциях     Изоспины ядер, возникающих в результате различных ядерных реакций, зависят как от изоспина ядра-мишени T0, так и от изоспина частиц, участвующих в реакции возбуждения. Изоспины ядер Tf, возникающих в результате реакций, приведены в таблице 1. Изоспин в ядерных реакциях Таблица 5.1 Реакция ΔT ΔT3 (e,e') 1.0 0 To, To+1 (γ,...) 1.0 0 To, To+1 (p,p') 0.1 0 To, To+1 (α,α') 0 0 To (p,n) 1 -1 To-1,To, To+1 (n,p) 1 +1 To+1 (π–,γ) 1 +1 To+1 (μ–,ν) 1 +1 To+1 (π,π) 2 +2 To+2 Рис.5.1. Ядро 14N    В реакциях сильного взаимодействия выполняется закон сохранения изоспина. Использование этого закона при анализе ядерных реакций является одним из способов идентификации значения изоспина. 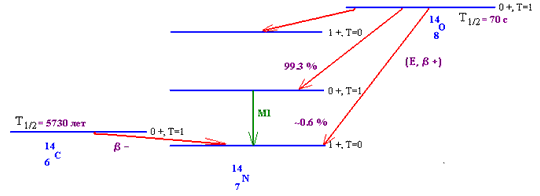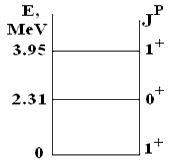Рассмотрим применение этого закона на примере ядерных реакций неупругого рассеяния частиц на ядре 14N.     Исследования ядерных реакций рассеяния с различными пробными частицами на этом ядре показали, что в неупругом рассеянии альфа-частиц (α,α')и в неупругом рассеянии дейтронов ядро 14N может оказаться в основном состоянии, а также в состоянии с Е=3.95 МэВ. Уровень с энергией 2.31 МэВ в этих реакциях не возбуждается! Это означало, что изоспин первого возбужденного состояния 14N не равен нулю. Действительно, по закону сохранения изоспина в реакциях с пробными частицами нулевого изоспина (5.1) ядро 14N может оказаться лишь в состоянии с изоспином 0: 0 + 0 = 0 + T →  T = 0.     Но в реакциях рассеяния протонов уровень с Е = 2.31 МэВ возбуждается!     Из закона сохранения изоспина в реакции с протонами следует, что в реакциях (p,p') могут быть возбуждены как состояния с изоспином 0, так и состояния с изоспином 1:     Сравнение результатов разных реакций приводит к выводу, что изоспин уровня Е = 2.31 МэВ равен 1.     Поскольку изоспин фотона принимает значения 0 и 1 [1], в фото- и электроядерных реакциях также возможно возбуждение состояний 14N с изоспинами 0 и 1. (Как реальный, так и виртуальный γ-квант в процессе рассеяния или поглощения может передать изоспин, равный 0 либо 1.) 6. Расчет вероятностей изоспиновых возбуждений     Матричные элементы операторов изовекторного возбуждения зависят от изоспинов начального и конечного состояний ядра через соответствующие коэффициенты векторного сложения: (6.1) Здесь Tg.s. – изоспин основного состояния ядра-мишени, T3 – его проекция. Формула (1.2) соответствует изовекторному возбуждению ядра в реакциях фото- и электровозбуждения, в которых проекция изоспина ядра не изменяется. (Формула (6.1) является формулировкой закона Вигнера-Эккарта в пространстве изоспина.).     Для ядер с изоспином основного состояния 0 в матричном элементе (м.э.) операторов возбуждения появляется множитель : (6.1а)     Поскольку эффективные сечения связаны с квадратами м.э., изоспиновый множитель в расчетах сечений (либо формфакторов) ядер с изоспином основного состояния Tg.s. = 0 равен 1/3.     (Следует отметить, что формула (6.1) является одновременно определением приведенного по изоспину матричного элемента .) (6.2) В соответствии с (6.1) в расчет сечений изовекторных возбуждений ядер (МГР) должны быть введены изоспиновые коэффициенты К2: (6.3)     Для ядер с изоспином основного состояния Т0 = 1/2 распределение ветвей возбуждения по изоспину соответствует результату оценок по формуле (6.1). Возбуждение двух ветвей равновероятно, изоспиновый коэффициент в сечениях этих ветвей (или квадратах формфакторов) равен 1/6.     Расчет вероятностей возбуждения изоспиновых состояний для всех ядер с Т0 ≠ 0 показывает, что состояния с изоспином T< имеют большую вероятность возбуждения чем T>. Например, расчет К для ядер с изоспином основного состояния Т = 1 дает (6.4)     Вероятности изовекторного возбуждения ветвей мультипольного резонанса в зависимости от изоспина ядра-мишени приведены в Таблице 6.1: Изоспиновые коэффициенты К (см. 6.2) Таблица 6.1 T0 0 1 2 3 4 W(T<) Т=1 T< = 1 T> = 2 T< = 2 T< = 3 T< = 3 T> = 4 T< = 4 T> = 5 W(T>) 1/3 1/6 1/10 2/15 1/21 3/28 1/36 4/45 1/55     Видно, что по мере увеличения изоспина основного состояния ядра, ветвь T> играет все меньшую роль в изовекторном фото- и электровозбуждении. 7. Роль изоспина в распадах возбужденных состояний ядер.     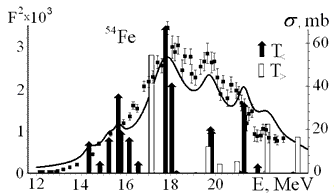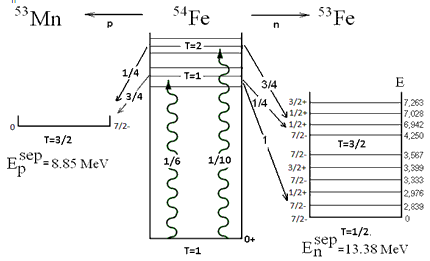Изоспиновые факторы, определяющие вероятности распадов по нейтронному и протонному каналам распадов возбужденных ядер , соответствуют квадратам следующих коэффициентов векторного сложения : (7.1)     Роль изоспина в возбуждении и распаде ядерных состояний хорошо видна на примере дипольного резонанса в ядре 54Fe [7]. Зависимость ядерных взаимодействий от величины изоспина приводит к изоспиновому расщеплению уровней Е1 резонанса (рис. 7.1). Теоретическое описание Е1 резонанса [7] показало, что среднее значение энергий уровней с изоспином T> = 2 выше, чем уровней с T< = 1 (рис.7.1). Рис.7.1. Сравнение теоретического и экспериментального 54Fe(γ,n) распределений [7].     Изоспиновые факторы изовекторного возбуждения и распада ядра 54Fe по нейтронному и протонному каналам приведены на рис.7.2 . Распад ветви Т = 2 в основное состояние ядра 53Fe запрещен по изоспину. Рис.7.2. Распределение изоспиновых факторов в возбуждении и нуклонных распадах ядра 54Fe. Литература C.Amsler et al //Phys.Lett.B 667,1 (2008) Б.С.Ишханов, И.М.Капитонов, Н.П.Юдин, Частицы и атомные ядра, URSS,М.2019 P.D.Cottle et al //Phys.Rev.Lett.88,172502 (2002) A.M.Lane //Nucl.Phys. 35,676 (1962) R.O. Akyűz, S.Fallieros // Phys.Rev.Lett.27,1016 (1971) J. D. Anderson and C. Wong// Phys. Rev. Letters 7, 250 (1961); H. Feshbach//Comments on Nuclear and Particle Physics 1, 40 (1967) 7. Н. Г. Гончарова, А. П. Долгодворов //Ядерная Физика, 77, 223 (2014)