|
|
|
(1.1) |
Для реальных частиц, которые могут быть зарегистрированы
детектором, полная энергия всегда положительна, а условие (1.1) всегда
выполняется. Таким образом, состояния реальной частицы с массой т в импульсном
пространстве заполняют гиперповерхность, выделенную двумя условиями:
![]() 2 = m2
и Е ≥ m.
2 = m2
и Е ≥ m.
Какие бы события взаимодействия частиц ни происходили, они
происходят так, что сохраняется не только привычный полный трехмерный импульс,
но и полная энергия. Поэтому сохраняется и "длина" вектора полного 4-импульса:
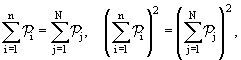 |
(1.2) |
где ![]() i
есть 4-импульс i-й частицы начального состояния, п есть число частиц в начальном
состоянии, N − число частиц после взаимодействия (оно не обязательно равно n),
i
есть 4-импульс i-й частицы начального состояния, п есть число частиц в начальном
состоянии, N − число частиц после взаимодействия (оно не обязательно равно n),
![]() j (
j (![]() i) −
4-импульс отдельной частицы соответствующего состояния.
i) −
4-импульс отдельной частицы соответствующего состояния.
Именно анализ следствий этого закона является основной
задачей релятивистской кинематики элементарных процессов.
* * *
Согласно специальной теории относительности, законы
природы одинаковы во всех инерциальных системах отсчета. В применении к
кинематике это означает, что для описания кинематических событий необходимо,
во-первых, знать законы преобразования компонент 4-импульса при переходе от
одной системы отсчета к другой, и во-вторых, необходимо стремиться к описанию
этих событий в терминах таких переменных, которые не изменяются при переходе от
одной системы отсчета к другой (такие переменные называются лоренц-инвариантными;
при обсуждении вопросов кинематики их часто называют просто "инварианты").
Напомним элементарные свойства 4-векторов, под которыми
понимается совокупность четырех величин A0, A1, A2,
A3, испытывающих при преобразованиях четырехмерных координат
изменения согласно преобразованиям Лоренца
[9]. Принято записывать такую совокупность как Aµ, µ = 0, 1, 2, 3 или
![]() = (A0,
A1, A2, A3) или
= (A0,
A1, A2, A3) или
![]() = (A0,
A). Квадрат величины
= (A0,
A). Квадрат величины
![]() (аналог квадрата
модуля привычного трехмерного вектора) определяется как
(аналог квадрата
модуля привычного трехмерного вектора) определяется как
![]() = (A0)2 − (A1)2 − (A2)2 −
(A3)2.
= (A0)2 − (A1)2 − (A2)2 −
(A3)2.
В зависимости от знака величины
![]() 2
множество 4-векторов расщепляется на 3 класса: при
2
множество 4-векторов расщепляется на 3 класса: при
![]() 2 > 0
они принадлежат классу времени-подобных 4-векторов, класс 4-векторов с
2 > 0
они принадлежат классу времени-подобных 4-векторов, класс 4-векторов с
![]() 2 < 0
называется пространственно-подобным, а 4-векторы, для которых
2 < 0
называется пространственно-подобным, а 4-векторы, для которых
![]() 2 = 0,
составляют класс изотропных 4-векторов. Эта классификация релятивистски
инвариантна. Свободно движущиеся частицы с ненулевой массой имеют времени-подобный вектор 4-импульса, а частицы с нулевой массой - изотропный.
Обсуждая кинематику физических процессов, экспериментатор имеет дело, как
правило, с реальными частицами, поэтому соответствующие 4-импульсы физических
реальных частиц времени-подобны или изотропны (если масса частицы нулевая,
как у фотона). Для виртуальных частиц их 4-импульс может принадлежать любому из
классов.
2 = 0,
составляют класс изотропных 4-векторов. Эта классификация релятивистски
инвариантна. Свободно движущиеся частицы с ненулевой массой имеют времени-подобный вектор 4-импульса, а частицы с нулевой массой - изотропный.
Обсуждая кинематику физических процессов, экспериментатор имеет дело, как
правило, с реальными частицами, поэтому соответствующие 4-импульсы физических
реальных частиц времени-подобны или изотропны (если масса частицы нулевая,
как у фотона). Для виртуальных частиц их 4-импульс может принадлежать любому из
классов.
В дальнейшем обсуждении вопросов кинематики элементарных
процессов подразумевается, что речь идет о массивных частицах (например, при
обсуждении 4-скорости); специальные случаи кинематики с участием фотонов
оговариваются отдельно.
Запись вида Aµ соответствует т. н.
контравариантному 4-вектору
![]() . Если определить
новый 4-вектор с компонентами
. Если определить
новый 4-вектор с компонентами
| A0 = A0, A1 = -A1, A2 = -A2, A3 = -A3 | (1.3) |
и записать их как Aµ, то величину
![]() 2 можно
переписать в форме
2 можно
переписать в форме
![]() 2
=
2
= ![]() AµAµ
= A0A0 + A1A1 + A2A2
+ A3A3,
AµAµ
= A0A0 + A1A1 + A2A2
+ A3A3,
что принято записывать просто как AµAµ, опуская знак
суммирования, но подразумевая, что по совпадающим индексам, встречающимся и
вверху, и внизу, производится суммирование.
Можно убедиться, что закон преобразования
ковариантного вектора Aµ почти такой
же, как в формулах (1.8, 1.11), отличаясь только знаком Γ в них, противоположным
по отношению к знаку Γ в формулах преобразования для
контравариантного вектора Aµ.
Скалярное произведение двух 4-векторов
![]() и
и
![]() определяется как
определяется как
|
|
(1.4) |
Можно легко убедиться непосредственным вычислением, что величина (![]() ·
·![]() )
действительно инвариантна относительно преобразований Лоренца, т. е. является
скаляром в пространстве определенных здесь 4-векторов.
)
действительно инвариантна относительно преобразований Лоренца, т. е. является
скаляром в пространстве определенных здесь 4-векторов.
Важную роль в исчислении четырех-векторов играет
метрический тензор gµν = gµν,
до сих пор не встречавшийся здесь, но с которым при чтении рекомендованной
литературы читатель непременно встретится. Подозревая, что читатель с ним уже
знаком и помня, что "лучше поздно, чем никогда", напомним и о нем.
Метрический тензор gµν представляется в виде
матрицы
g = (gµν) = (gµν)
=
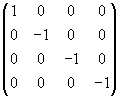 =
g-1. =
g-1. |
(1.5) |
С его помощью можно, например, переводить контравариантные 4-векторы в ковариантные и наоборот:
| Aµ = gµνAν, Aµ = gµνAν, | (1.6) |
(Здесь использовано данное выше соглашение о суммировании повторяющихся индексов.) Скалярное произведение двух 4-векторов с помощью этого тензора записывается очень просто:
| ( |
(1.7) |
Почему тензор gµν называется "метрическим",
любопытствующий читатель может узнать из литературы, например, из книги [5].
Более подробное рассмотрение свойств 4-векторов можно найти,
в частности, в книгах [5, 9] и многих других.
* * *
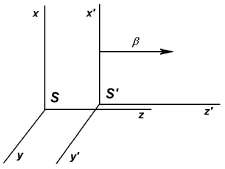 Рис. 1.1. Штрихованная система движется относительно нештрихованной со скоростью β. Соответственно, система S относительно системы S' движется со скоростью -β. |
Итак, компоненты 4-вектора
![]() = (E, p)
при переходе от одной системы отсчета к другой испытывают преобразования Лоренца.
Настала пора их напомнить.
= (E, p)
при переходе от одной системы отсчета к другой испытывают преобразования Лоренца.
Настала пора их напомнить.
Пусть в какой-то системе отсчета S частица имеет импульс p
и энергию E. Пусть другая система отсчета S' движется относительно S со
скоростью β так, как показано на рисунке 1.1.
Тогда импульс p' и энергия E' этой же частицы в системе отсчета S' будут
связаны с p и E системе S соотношениями
| E' = γE − Γ p' = ( |
(1.8) |
где ![]() и
и
![]() − компоненты соответствующих импульсов, параллельные вектору
скорости (3 (вдоль которой направлены, например, оси Z и Z' систем координат
обеих систем отсчета),
− компоненты соответствующих импульсов, параллельные вектору
скорости (3 (вдоль которой направлены, например, оси Z и Z' систем координат
обеих систем отсчета),
![]() и
и
![]() − компоненты этих импульсов, перпендикулярные
вектору скорости β (вдоль этого перпендикуляра направлены, например, оси X и X'
принятых нами систем координат), а величины γ и Γ есть
− компоненты этих импульсов, перпендикулярные
вектору скорости β (вдоль этого перпендикуляра направлены, например, оси X и X'
принятых нами систем координат), а величины γ и Γ есть
| γ = 1/(1 − β2)1/2. Γ = β/(1 − β2)1/2. | (1.9) |
Здесь для произведения γβ использовано удачное обозначение Γ из книги Г.И.Копылова [2], благодаря которому преобразование Лоренца (1.8) записывается в легко запоминающейся форме.
Если частица в системе отсчета S имеет импульс p и энергию E, то ее система покоя движется относительно S-системы с той же скоростью, что и эта частица, а именно:
| β = p/E, γ = E/m, Γ ≡ γβ = p/m. | (1.10) |
Преобразование (1.8) можно записать для любого 4-вектора
![]() = (A0,A) ≡
(A0,A1,A2,A3) = (A0,Ax,Ay,Az). To есть, при переходе из нештрихованной системы S
= (A0,A) ≡
(A0,A1,A2,A3) = (A0,Ax,Ay,Az). To есть, при переходе из нештрихованной системы S
(рис. 1.1) в штрихованную его компоненты преобразуются согласно
| A'0 = γ(A0
− βA3) = γA0 − ΓA3, A'1 = A1, A'2 = A2, A'3 = γ(A3 − βA0) = γA3 − ΓA0. |
(1.11) |
В матричной записи это преобразование выглядит следующим образом:
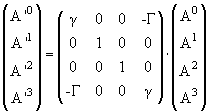 |
(1.12) |
Примечательно, что если ввести 4-вектор
![]() = (γ,Г)*, имеющий свойство
= (γ,Г)*, имеющий свойство
![]() 2
= γ2 − Г2 = 1, то формулы (1.11) можно переписать в виде
2
= γ2 − Г2 = 1, то формулы (1.11) можно переписать в виде
| A'0 =
A'3 = (A3 − Γ |
(1.13) |
* * *
В современной физике частиц характеристики их взаимодействий описываются, как
правило, в терминах лоренц-инвариантных кинематических переменных. О них речь
пойдет позже. Широко употребляются также безразмерные переменные, одной из
которых является быстрота (или относительная быстрота; ранее для нее
использовался термин гиперскорость [2]). Напомним ее определение.
Как известно, если сделать два последовательных преобразования вида (1.11) с
параметрами β1 и β2 при условии, что направления движения систем отсчета S1 и
S2 параллельны (обозначения здесь очевидны), то полученный результат будет
эквивалентен одному преобразованию с параметром β3 вдоль того же направления:
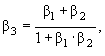 γ3 = γ1
− γ2·(1 + β1·β2) = γ1 ·γ2 + Γ1·Γ2, γ3 = γ1
− γ2·(1 + β1·β2) = γ1 ·γ2 + Γ1·Γ2, |
(1.14) |
что можно переписать в симметричном виде как
| γ3 = γ1·γ2 + Γ1·Γ2, Γ3 = Γ1γ2 + γ1Γ2. | (1-15) |
Определим быстроту ξ (или гиперскорость) согласно
| β = tanh ξ, γ = cosh ξ, Γ ≡ β·γ = sinh ξ; | (1-16) |
после этого нетрудно убедиться, что соотношения (1.15) в терминах быстрот означают, что
| ξ3 = ξ1 + ξ2. | (1-17) |
Иными словами, при параллельных друг другу преобразованиях Лоренца быстроты
складываются.
Более подробное обсуждение этой переменной будет проведено позже; можно также
обратиться за деталями к рекомендованным книгам по кинематике**. Здесь важно
подчеркнуть именно это свойство аддитивности быстрот при параллельных
преобразованиях Лоренца.
Матричная запись преобразования (1.12) при использовании быстроты η выглядит
следующим образом:
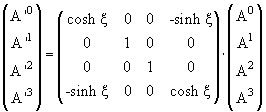 |
(1.18) |
Наконец, из соотношений (1.16), (1.18) становится почти очевидным, что рассмотренные здесь преобразования Лоренца фактически есть не что иное, как преобразования вращения в 4-мерном пространстве. Появление гиперболических функций вызвано тем, что это пространство не является евклидовым. Однако более подробное обсуждение этих вопросов выходит за рамки данного курса.
* Фактически, 4-вектор
![]() = (γ,Г) есть не что иное, как 4-скорость. Это
понятие будет рассмотрено позже.
= (γ,Г) есть не что иное, как 4-скорость. Это
понятие будет рассмотрено позже.
** Об определении быстроты для фотонов − см. [2].