ЭКЗОТИЧЕСКИЕ ДЫРОЧНЫЕ СОСТОЯНИЯ АТОМОВ, ОБРАЗУЕМЫЕ В ПОЛЕ РЕНТГЕНОВСКОГО ЛАЗЕРА НА СВОБОДНЫХ ЭЛЕКТРОНАХ:
ДВОЙНЫЕ K-ВАКАНСИИ В НЕОНЕ

М.Д. Киселев¹, Е.В. Грызлова¹, А.Н. Грум-Гржимайло¹, O. Zatsarinny^2
1Научно-исследовательский институт ядерной физики МГУ; ^<2Department of Physics and Astronomy, Drake University, Des Moines, Iowa, USA
E-mail: md.kiselev94@gmail.com

     Интенсивные импульсы рентгеновских лазеров на свободных электронах (XFEL) дают возможность исследования нелинейных фотопроцессов в атомах и молекулах в коротковолновом диапазоне. Они включают, в частности, процессы последовательной и прямой многофотонной ионизации и возбуждения. Последовательная ионизация из внутренних электронных подоболочек конкурирует с быстрой релаксацией дырок посредством оже-распада [1]. При интенсивном рентгеновском облучении могут поглотиться более одного фотона в течение нескольких фемтосекунд, прежде чем произойдёт оже-распад вакансии. Тогда вклад такого последовательного фотопоглощения  электронов остова и, соответственно, относительная заселённость промежуточных высоковозбуждённых ионных состояний с двумя, а возможно и более, дырками во внутренних оболочках значительно возрастает. Например, последовательное поглощение двух фотонов электронами K-оболочки неона может происходить двумя ступенями по схемам:

Первая ступень:
γ_XFEL + Ne (1s²2s²2p⁶)  →  Ne⁺ (1s¹2s²2p⁶) + e₁ (ионизация 1-го K-электрона)      (1)

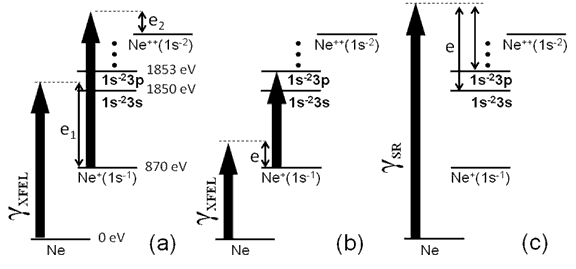
Вторая  ступень (энергия  фотона  выше  порога  ионизации К-электрона в ионе Ne⁺  (1s¹2s²2p⁶)):
γ_XFEL + Ne⁺ (1s¹2s²2p⁶)  → Ne⁺⁺  (1s⁰2s²2p⁶) + e₂ (ионизация 2-го K-электрона)   (2)
или (энергия фотона ниже порога ионизации К-электрона в ионе Ne⁺(1s¹2s²2p⁶)):
γ_XFEL + Ne⁺ (1s¹2s²2p⁶) → Ne⁺  (1s⁰2s²2p⁶np) (возбуждение 2-го K-электрона).    (3)

    В экспериментах с источниками синхротронного излучения (SR) третьего поколения тоже можно наблюдать двойные K-вакансии [2], но только возбуждаемые одним фотоном: для поглощения второго фотона до оже-распада вакансии не хватает интенсивности излучения. В этом случае при поглощении одного фотона первый электрон ионизуется, а второй либо «встряхивается» (shake-up) на не занятую валентную оболочку

γ_SR + Ne (1s²2s²2p⁶)  →  Ne⁺  (1s⁰2s²2p⁶ ns/np) + e       (4)

либо «вытряхивается» (shake-off)  в непрерывный спектр:

γ_SR + Ne (1s²2s²2p⁶)  →  Ne⁺⁺  (1s⁰2s²2p⁶) + e₁ + e₂      (5)

    Рис.1 иллюстрирует процесс образования двойной К-вакансии в атоме неона при последовательной двойной двухфотонной ионизации импульсом XFEL (рис.1а,b) и при двойной однофотонной ионизации синхротронным излучением (рис.1c).
    Процесс (1)+(2) (рис. 1a) наблюдался экспериментально и рассчитывался теоретически [1]. Процесс (4) (рис. 1с) наблюдался и теоретически анализировался в [2]. В этой работе мы концентрируемся на теоретическом изучении процесса (1)+(3) (рис. 1b), который является резонансным и происходит, когда энергия рентгеновского фотона соответствует энергии перехода Ne⁺ (1s¹2s²2p⁶) → Ne⁺ (1s⁰2s²2p⁶np). Конкретные расчеты проводятся для резонанса с n = 3.

Рис. 1. Схемы образования двойной К-вакансии в атоме неона. (а) – последовательная двойная двухфотонная ионизация импульсом XFEL с вылетом двух К-электронов; (b) – последовательная двойная двухфотонная ионизация импульсом XFEL с вылетом одного К-электрона и возбуждением второго в состояние с конфигурацией 1s⁰2s²2p⁶np; (c) – однофотонная ионизация синхротронным излучением с вылетом одного К-электрона и встряской второго К-электрона. Указаны экспериментальные значения энергий [2].

    Расчёты фотопоглощения в процессе (3) проводились методом R-матрицы с помощью программного комплекса BSR (B-Spline R-matrix) [3]. В основе метода лежит разделение пространства на две части: ограниченную внутреннюю область, в которой можно ввести удобный базис квадратично-интегрируемых функций, позволяющих сделать хорошую аппроксимацию радиальных частей электронных орбиталей с учётом взаимодействий в многоэлектронной системе, и внешнюю область, в которой взаимодействие частей исследуемой системы хорошо описывается известными дальнодействующими потенциалами. В качестве базисных функций во внутренней области в программе BSR выбраны B-сплайны. В расчетах используется приближение LS-связи  и  неортогональные  электронные орбитали. Эта неортогональность полностью учитывается при вычислении матричных элементов. Расчёты электронных орбиталей для начального и конечного связанных состояний проводились многоконфигурационным методом Хартри-Фока с помощью программы MCHF [4]. Все энергии в представленных ниже результатах взяты из наших расчётов, если не оговорено особо.

Таблица 1. Учитываемые в расчетах конфигурации остаточного иона Ne ⁺⁺.

     Состояние Ne⁺ (1s⁰2s²2p⁶3p  ²P) распадается с испусканием оже-электрона, и весь процесс образования короткоживущей двойной К-вакансии и последующего её распада является так называемым «резонансным процессом Оже», который является частным случаем резонансной фотоионизации. Для проведения фотоионизационных расчётов методом R-матрицы необходимо задать набор многоэлектронных конфигураций остаточного фотоиона («пороги»), в нашем случае – конфигураций двукратно заряженного иона неона. Этот набор порогов определяет каналы оже-распада и приведён в табл. 1. Возможны два варианта оже-распада состояния Ne⁺ (1s⁰2s²2p⁶3p ²P), указанные в табл. 1: когда 3p-электрон активен, т.е. непосредственно участвует в оже-распаде двойной вакансии, и когда 3p-электрон пассивен («спектатор»), т.е. не участвует в оже-распаде и остаётся после распада на 3p-оболочке.

Рис. 2. Сечение фотопоглощения иона неона с одной К-вакансией Ne⁺ (1s¹2s²2p⁶) в области Ne⁺ (1s⁰2s²2p⁶3p) резонанса. Сплошная линия – учитываются только распады с активным 3p-электроном (5 порогов в табл. 1); пунктирная линия – учитываются распады с активным и пассивным 3p-электроном (все 27 порогов из табл. 1); точечная линия – учитываются распады с активным 3p-электроном и пассивными 3p- и 4p-электронами (49 порогов: 27 порогов из табл. 1 и 22 порога с 4p-электроном, аналогичных конфигурациям с пассивным 3p-электроном, представленным в табл. 1). Стрелкой указано пиковое значение сечения фотопоглощения для сплошной линии. Энергия фотонов из расчёта. a_B – боровский радиус.

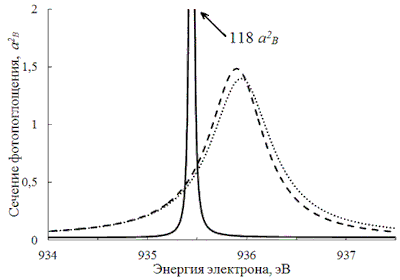
    На рис. 2 показаны сечения фотопоглощения, рассчитанные с разными наборами порогов. Добавление мод распада с пассивным 3p-электроном критически меняет форму спектра  фотопоглощения,  а  ширина  резонанса  увеличивается  почти на два порядка. Напротив, пороги, открывающие каналы распада с пассивным 4p-электроном (аналогичные 22-м каналам с пассивным 3p-электроном, указанным в табл. 1), практически не меняют сечение в области 3p-резонанса, а незначительная сдвижка пика объясняется изменением энергий порогов за счёт смешивания с добавленными конфигурациями с 4p-электронами. С увеличением главного квантового числа np-электрон всё больше удаляется от ионного остова и его участие в оже-распаде всё меньше. Таким образом, наши расчеты для наименьшего значения n = 3 указывают на то, что распады с пассивными np-электронами являются определяющими для правильного описания релаксации системы с двойной вакансией и сечений фотопоглощения в области соответствующих Ne⁺(1s⁰2s²2p⁶np) резонансов.

Рис. 3. Спектр фотоэлектронов, свёрнутый с гауссовской функцией распределения по энергии фотонов в пучке и с учётом гауссовской аппаратной функции электронного детектора при трёх различных центральных частотах падающего фотона, указанных на рисунке. Ширина на половине высоты распределений 10 эВ для фотонного пучка и 1 эВ для электронного спектрометра.

    Полученные при расчёте сечения фотопоглощения парциальные вклады от фотоионизации на определенные конечные состояния иона Ne⁺⁺ позволяют, путём простого пересчёта энергетической шкалы, получить спектр фотоэлектронов (оже-электронов). На рис. 3 мы приводим небольшой участок такого спектра с учётом типичной для таких энергий XFEL шириной фотонного пучка и разрешающей способности электронного детектора. 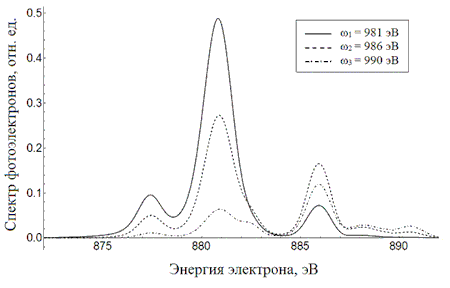Спектр соответствует постановке эксперимента с детектированием электронов на совпадения с зарядовым состоянием иона, в данном случае двухзарядным ионом Ne⁺⁺. В спектре можно выделить 3 основных максимума. Максимум при энергии 877 эВ соответствует двум не разрешенным по энергии линиям от распада резонанса Ne⁺(1s⁰2s²2p⁶3p) на состояния Ne⁺⁺(1s¹2s²2p⁴(²S)3p^{1 1,3}P) (см. табл. 1). Средний максимум при 881 эВ образован шестью линиями от распада этого 3p-резонанса на различные термы конфигурации Ne⁺⁺(1s¹2s²2p⁴(²D)3p¹) , а максимум при энергии 886 эВ – линиями от распада 4p-резонанса на состояния Ne⁺⁺(1s¹2s²2p⁴3p). При увеличении энергии фотона меняется относительный вклад резонансов в фотоэлектронный спектр: если при энергии фотона 981 эВ 3p-резонанс сильно доминирует над 4p-резонансом, то при энергии фотона 986 эВ вклады от этих двух резонансов становятся сопоставимыми.
    В заключение, в работе методом R-матрицы получены сечение фотопоглощения и спектры фотоэлектронов при ионизации иона c K-вакансией Ne⁺(1s¹2s²2p⁶) в области оже-состояния с двойной К-вакансией Ne⁺(1s⁰2s²2p⁶3p). Доминирующими каналами оже-распада состояния 1s⁰2s²2p⁶3p, как и вообще состояний с двумя К-вакансиями Ne⁺(1s⁰2s²2p⁶np) являются каналы с пассивным возбужденным np-электроном. Полученные результаты представляют интерес для экспериментов на рентгеновских лазерах на свободных электронах.
    Мы выражаем благодарность сотрудникам Европейского XFEL М. Мейеру (M. Meyer) и Т. Мацца (T. Mazza) за интерес к работе и плодотворные обсуждения. Работа Е.В.Г. и М.Д.К. была поддержана грантом Фонда развития теоретической физики и математики «Базис».

1. L. Young et al. Nature, v. 466, pp. 56-61,  2010.
2. G. Goldzstejn et al. Phys. Rev. Lett., v. 117, pp. 133001(1)-(5), 2016.
3. O. Zatsarinny. Comp. Phys. Commun. v. 174, pp. 273-356, 2006.
4. C. Froese Fischer, T. Brage and P. Jönsson “Computational Atomic Structure: an MCHF  Approach”. Bristol: IOP Publishing, 1997.