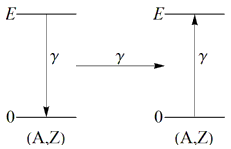
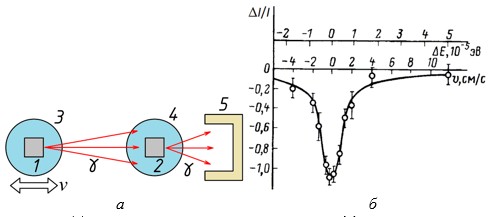
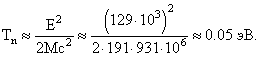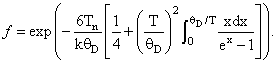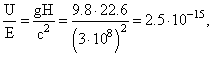И. Владимиров Эффект Мессбауэра и его применение Введение     Эффект Мессбауэра – это пример физического явления, которое нашло применение во многих областях науки: химии, ядерной физике, физике твердого тела и т.д. Данная работа не является полным и всесторонним обзором применений эффекта Мессбауэра, а призвана объяснить читателю суть эффекта Мессбауэра и показать, что открытие этого эффекта имело большое фундаментальное и практическое значение для науки в целом. Также автор надеется, что данная работа послужит стимулом для читателя к дальнейшему более глубокому изучению эффекта Мессбауэра. 1. Резонансное поглощение γ-излучения     В 1958 г. в физике γ-излучения было сделано интересное открытие, получившее по имени автора название эффект Мессбауэра. Этот эффект является ядерным аналогом резонансной флуоресценции и состоит в том, что если одно ядро испускает γ-квант, то другое такое же ядро с большой вероятностью этот квант поглощает (рис. 1). До 1958 г. наблюдение резонансного поглощения γ-квантов ядрами считалось невозможным по следующим соображениям. Рис. 1. Резонансное поглощение γ-квантов ядрами (A, Z)     При γ-распаде ядро некоторое время τ находится в возбужденном состоянии, а затем испускает фотон. Согласно соотношению неопределенностей энергия возбужденного состояния E известна с погрешностью Γ: Г = ћ/τ .     Чем быстрее происходит переход из возбужденного состояния, тем больше неопределенность в значении энергии возбужденного состояния. Неопределенность в энергии возбужденного состояния приводит к немонохроматичности γ-излучения, испускаемого при переходе ядра из возбужденного состояния в основное. Эта немонохроматичность называется естественной шириной Γ линии испускания γ-излучения [1].     Рассмотрим для примера ядро иридия 191Ir, находящееся в возбужденном состоянии с энергией E=129 кэВ, из которого оно может перейти в основное состояние в результате испускания γ-кванта с периодом полураспада T1/2 ≈ 10−10 с (рис. 2). Естественная ширина линии испускания равна:     Это очень малое значение по сравнению с энергией γ-перехода E: Γ/E ≈ 4∙10−11. Рис. 2. Схема образования изотопа 191Ir     При γ-излучении из ядра вылетает фотон. По закону сохранения импульса ядро получает импульс отдачи pn, равный по абсолютной величине импульсу фотона pγ: 0 = n + γ pn = pγ.     Соответственно ядро приобретает кинетическую энергию , где M – масса покоя ядра. Из закона сохранения энергии E = pγc + Tn следует, что энергия pγc вылетающего фотона не точно равна энергии перехода E. Энергия перехода делится между фотоном и ядром отдачи. 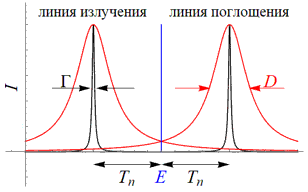Поскольку энергия перехода E много меньше энергии покоя ядра Mc2, энергия отдачи Tn с хорошей точностью определяется формулой Энергия, которую уносит γ-квант, оказывается меньше энергии перехода E: pγc = E – Tn < E. Аналогично для возбуждения ядра до энергии E необходимо γ‑излучение с энергией pγc = E + Tn > E. Таким образом, линия испускания и линия поглощения для одного и того же состояния в ядре сдвинуты относительно друг друга на 2Tn (рис. 3). Рис. 3. 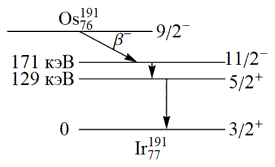Сдвиг линий испускания и поглощения одного и того же состояния в ядре, естественные (черные) и доплеровские (красные) уширения линий     Для изотопа 191Ir, испускающего фотон из первого возбужденного состояния или поглощающего фотон для перехода в первое возбужденное состояние, энергия отдачи оказывается небольшой:     Но эта энергия существенно превышает естественную ширину линии излучения Γ ≈ 5∙10−6 эВ. Отсюда должна следовать абсолютная невозможность резонансного поглощения. Но это неверно, потому что реальная ширина линий испускания и поглощения определяется не естественной шириной Γ, а доплеровским уширением, которое при комнатной температуре равно [1]:     Так как D ≈ Tn, то доплеровски уширенные линии испускания и поглощения частично перекрываются (рис. 3) и резонансный процесс становится возможным. Но он не обладает большой остротой, так как D/E ≈ 0.5∙10−6, и наблюдается только для очень малого количества γ‑квантов, соответствующих небольшой области перекрытия линий [1]. 2. Опыты Мессбауэра Рис. 4. Рудольф Людвиг Мессбауэр (1929–2011). В 1961 г. получил Нобелевскую премию по физике за эффект, названный в его честь – эффект Мессбауэра     В 1958 г. немецкий физик Мессбауэр (рис. 4), проводя опыты по изучению резонансного поглощения в условиях частичного перекрытия линий в результате их доплеровского уширения, решил уменьшить D при помощи охлаждения источника и поглотителя. При этом ожидалось уменьшение доли поглощенных фотонов из-за сокращения области перекрытия линий. Вместо этого в опыте было обнаружено увеличение эффекта, которое свидетельствовало о возрастании области перекрытия.     Мессбауэр объяснил увиденное им явление следующим образом. На свободных ядрах резонансное поглощение не идет. Ядра источника и поглотителя находятся в кристаллической решетке. По законам классической механики при переходе от свободного ядра к твердому телу – кристаллу – ситуация не изменяется. Под влиянием сил кристаллических связей эффект отдачи смягчается, но далеко не настолько, чтобы сделать возможным резонанс. Однако амплитуда отдачи столь мала, что необходимо не классическое, а квантовое рассмотрение. В квантовой механике влияние кристаллической связи проявляется не так, как в классической механике, а статистическим образом. В большинстве случаев ядра источника и поглотителя испытывают полную отдачу. Но в небольшом проценте случаев испускание и поглощение γ-квантов идет без отдачи. При таких переходах и происходит резонансное поглощение. Условия для переходов без отдачи тем благоприятнее, чем ниже энергия перехода и чем ниже температура кристалла. Хотя для некоторых изотопов вполне заметный эффект удается наблюдать даже при комнатных температурах [2].     На рис. 5, а изображена схема опыта для наблюдения эффекта Мессбауэра. Источник 1 γ-излучения движется с малой постоянной скоростью в направлении поглотителя 2 или обратно. Источник и поглотитель состоят из одних и тех же ядер и помещены в криостаты 3 и 4, в которых поддерживается низкая температура. За поглотителем расположен счетчик 5. Измеряется зависимость скорости счета счетчика от скорости источника. Если скорость источника достаточно велика, то линия испускания сдвигается благодаря эффекту Доплера, так что резонансного поглощения нет. При уменьшении скорости доплеровский сдвиг уменьшается, а линия испускания начинает приближаться к линии поглощения. Когда эти линии пересекутся, начнется интенсивное резонансное поглощение. В результате скорость счета резка падает, как это изображено на рис. 5, б. Таким образом, плавно меняя скорость, можно измерить положение и ширину мессбауэровской линии (или линий, если их несколько) [2]. Рис. 5. (а) Схема эксперимента для наблюдения эффекта Мессбауэра. (б) Результат опыта Мессбауэра. По оси абсцисс отложены относительная скорость v источника и поглотителя и соответствующее ей изменение энергии ΔE испускаемых γ-квантов. По оси ординат отложена относительная разность интенсивности ΔI/I γ-излучения, проходящего через иридиевый и платиновый (для оценки фона) поглотители одинаковой толщины.     Оценим, с какой скоростью v должно двигаться ядро, чтобы выйти из резонанса за счет эффекта Доплера. Для этого надо приравнять ширине уровня Γ приращение энергии ΔE фотона, возникающее при переходе к системе координат, движущейся со скоростью v. При малых скоростях v это приращение равно: ΔE = vE/c. Положив ΔE = Γ, получим для скорости оценку v = cГ/E.     Величина Γ/E для низколежащих ядерных уровней очень мала. Поэтому малые значения получаются и для скоростей. 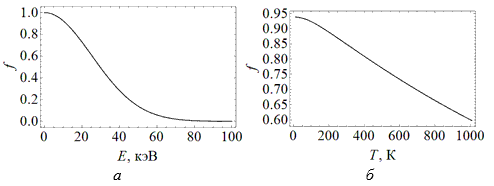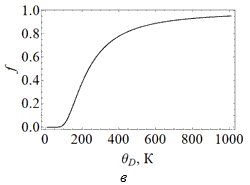Например, для изотопа иридия 191Ir скорость v получается равной 1.2 см/с. Такие скорости в лабораторных условиях легко осуществлять и измерять механически [2]. 3. Выбор веществ для исследования эффекта Мессбауэра     К настоящему времени эффект Мессбауэра наблюдался более чем для 40 элементов. Наиболее часто применяются изотопы железа 57Fe и олова 119Sn. Также довольно часто используются изотопы: 61Ni, 67Zn, 99Ru, 121Sd, 125Te, 129I, 151Eu, 155Gd, 166Er, 169Tm, 170Yb, 181Ta, 182W, 191Ir, 197Au, 237Np и т.д [3, 4]. Главными параметрами, которые оцениваются при выборе веществ для исследований с помощью эффекта Мессбауэра, являются коэффициент Мессбауэра f (доля процессов, происходящих без отдачи, 0 ≤ f  ≤1), достигаемая разрешающая способность, а также рабочая температура. 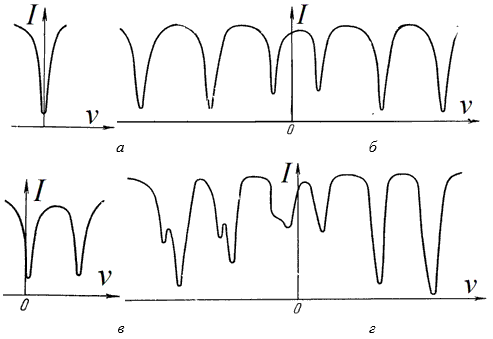Для одноатомных кристаллов коэффициент f можно оценить по формуле: Здесь θD – дебаевская температура, характеризующая упругость кристалла. Из формулы следует, что для большого f нужны малая отдача Tn, а значит низкая энергия перехода E, низкая температура T и высокая дебаевская температура θD (рис. 6, а-в). 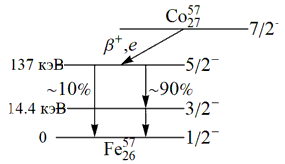Например, для изотопа железа 57Fe θD ≈ 500 K. На рис. 7 изображена схема перехода 57Fe из первого возбужденного состояния с энергией E = 14.4 кэВ в основное. Характеристики первого возбужденного состояния железа 57Fe такие: T1/2=1∙10−7 с, Γ= 4.5∙10−9 эВ, Γ/E=3∙10−13. На рис. 6, б показана зависимость коэффициента  f от температуры для этого изотопа. Из рисунка видно, что для 57Fe коэффициент Мессбауэра  f  > 0.6 вплоть до комнатной температуры T ≈ 300 К [1]. Рис. 6. (а) Зависимость коэффициента  f от энергии перехода E, если M = 57 ГэВ, T =300 К, θD ≈ 500. (б) Зависимость коэффициента  f от температуры T, если M = 57 ГэВ, E  =14.4 кэВ, θD ≈ 500. (в) Зависимость коэффициента f от дебаевской температуры θD, если M = 57 ГэВ, E=14.4 кэВ, T = 300 К. Рис. 7. Схема первых двух возбужденных уровней железа 57Fe. 4. Применение эффекта Мессбауэра Измерение красного смещения в лабораторных условиях     Эффект Мессбауэра интересен и уникален тем, что с его помощью измерение энергии можно производить с колоссальной точностью (до 15–17 порядков). Такая рекордная точность позволила, например, измерить зависимость энергии фотона от высоты источника за счет силы тяжести.     По общей теории относительности Эйнштейна фотон с энергией E должен вести себя в гравитационном поле как частица с массой m = E/c2. Если источник γ-излучения находится на расстоянии H ниже поглотителя, то фотон, двигаясь вверх к поглотителю, должен терять энергию, и его частота будет уменьшаться (красное смещение). Резонансные линии источника и поглотителя будут смещены относительно друг друга на потенциальную энергию U в поле силы тяжести U = mgh = EgH/c2, где g – ускорение свободного падения.     Опыт был выполнен в 1959 г. Паундом и Ребкой в башне Гарвардского университета высотой 22.6 м. При такой высоте относительное изменение энергии γ-кванта равно что примерно в 1.2∙102 раз меньше значения Γ/E ≈ 3∙10−13 для использованного в опыте изотопа 57Fe. Для надежного обнаружения эффекта необходимо было измерить энергию с абсолютной погрешностью 10−3Γ ≈ 4.5∙10−12 эВ. Это потребовало специальных условий проведения опыта: гелиевая среда между излучателем и поглотителем, контроль температуры, защита от вибраций [1]. Измерение сверхтонкого расщепления ядерных уровней     Сверхтонкое расщепление определяется произведением магнитного момента ядра μn на среднее магнитное поле He, создаваемое электронной оболочкой атома в области ядра. Поскольку магнитный момент ядра примерно равен ядерному магнетону μn ≈ 3.2∙10−8 эВ/Тл, а He ≈ 10 Тл, то величина сверхтонкого расщепления: ΔE = μnHe ≈  3.2∙10−8 ∙10 ≈ 3.2∙10−7 эВ     Сверхтонкое расщепление должно проявляться на фоне ядерных переходов. Так как относительное значение сверхтонкого расщепления ядерных уровней порядка ΔE/E ≈ 10-7/105 ≈10-12, расщепление такого масштаба можно измерить только с помощью эффекта Мессбауэра. Рис. 8. (а) Переходы между первым и основным уровнями железа 57Fe при учете сверхтонкого расщепления. 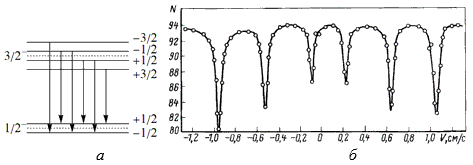(б) Мессбауэровская кривая для железа 57Fe     Впервые сверхтонкое расщепление ядерных уровней было обнаружено у изотопов железа 57Fe. На рис. 8, а показаны возможные переходы между первым и основным уровнями, испытавшими сверхтонкое расщепление. Такую структуру подуровней имеют как ядра излучателя, так и ядра поглотителя. Поэтому картина зависимости резонансного поглощения от скорости движения источника должна быть очень сложной. Для ее упрощения ядра излучателей включают в диамагнитную решетку из нержавеющей стали, из-за чего сверхтонкое расщепление для них отсутствует и число минимумов на мессбауэровской кривой совпадает с числом переходов в ядре поглотителя (рис. 8, б).     Расшифровка мессбауэровского спектра позволяет вычислить расщепления для основного ΔEосн и возбужденного ΔEвоз состояний. Это позволяет по измеренному значению ΔEосн и известному значению магнитного момента изотопа 57Fe в основном состоянии μnосн ≈ 2.8∙10−9 эВ/Тл вычислить среднее магнитное поле электронов в районе ядра: He =33.3 Тл. Далее, зная He и ΔEвоз, можно вычислить магнитный момент ядра в возбужденном состоянии: μnвоз ≈ −4.8∙10−9 эВ/Тл [1]. Измерение изомерного сдвига     Изомерный сдвиг проявляется в виде смещения центра тяжести спектра от нулевой скорости и обусловлен электростатическим взаимодействием ядра с окружающими электронами. Энергия этого взаимодействия различна для основного и возбужденного состояний, между которыми происходит γ-переход. Для того чтобы понять причину неравенства энергий перехода в источнике и поглотителе, требуется учесть, что ядра имеют конечный радиус. При этом у одних изотопов испускание γ-кванта может приводить к уменьшению, а у других – к увеличению размера ядра. 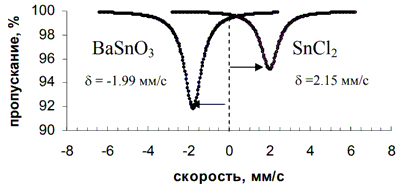Изменение радиуса ядра сопровождается изменением пространственного заряда ядра, что приводит к изменению энергии кулоновского взаимодействия ядерного заряда с электронным зарядом в месте нахождения ядра. Если химическое состояние мессбауэровских атомов источника и поглотителя одинаково (например, источником и поглотителем является SnO2), то смещение ядерных уровней в источнике и поглотителе за счет изменения радиуса ядра будет одинаковым. А потому энергии перехода между смещенными основным и возбужденным состояниями в источнике Es и поглотителе Ea будут тоже одинаковыми. Если же атомы в источнике и поглотителе находятся в химически различных состояниях (например, источником является SnO2, а поглотителем SnCl2), электронный заряд, с которым будет взаимодействовать ядро в атомах источника и поглотителя, будет различным. В результате Es будет отличаться от Ea и максимум резонансного поглощения проявится при v ≠ 0.     Для изомерного сдвига справедливо следующее выражение: где R = (Rосн + Rвоз)/2 – среднее значение радиуса ядра в возбужденном Rвоз и основном Rосн состояниях; ΔR = Rвоз – Rосн; Ψs и Ψa – волновые функции электронных оболочек атомов источника и поглотителя соответственно. Измерение изомерного сдвига позволяет исследовать изменение электронной структуры атомов в разных химических соединениях.     В качестве примера измерения изомерного сдвига на рис. 9 показаны мессбауэровские спектры для случаев, когда источником является α-модификация олова (“серое” олово), а поглотителями – SnCl2 и BaSnO3 [3]. Рис. 9. Мессбауэровские спектры двух соединений олова, полученные с источником α-модификация олова Исследования по физике твердого тела     Процессы, происходящие в атомных оболочках, оказывают ничтожное влияние на внутриядерные явления. С помощью эффекта Мессбауэра это влияние удается обнаружить. Линии мессбауэровских спектров заметно сдвигаются и меняются по ширине при переходе от одного химического соединения к другому, при изменении температуры, при наложении механических напряжений и т.д. Поэтому эффект Мессбауэра широко используется в исследованиях по физике твердого тела. Например, он оказался незаменимым для изучения фазовых переходов второго рода, при которых не меняется плотность, но меняется структура решетки.     Влияние кристаллической структуры на мессбауэровское излучение хорошо видно на рис. 10, а-г, где приведены мессбауэровские спектры изотопа железа 57Fe, снятые на различных железосодержащих образцах. На нержавеющей стали получается одиночная линия. На соединении FeCO3 эта линия раздваивается за счет действия градиента электрического поля. На окиси железа Fe2O3 получается уже шесть линий за счет расщепления внутренним магнитным полем. Еще большее количество линий имеет спектр магнетита Fe3O4. Здесь сказывается то, что в магнетите для атомов железа в решетке имеются два неэквивалентных положения. Грубо говоря, магнетит представляет собой комбинацию решеток Fe2O3 и FeO, вставленных друг в друга. Соответственно и мессбауэровский спектр магнетита состоит из двух наложенных друг на друга спектров Fe2O3 и FeO [2]. Рис. 10. Мессбауэровские спектры для изотопа железа 57Fe на различных железосодержащих образцах: (а) нержавеющая сталь, (б) гематит Fe2O3, (в) сидерит FeCO3, (г) магнетит Fe3O4 Заключение     Эффект Мессбауэра – резонансное возбуждение ядерных уровней фотонами от источника из того же вещества. Трудность наблюдения резонансного возбуждения связана с тем, что естественная ширина ядерных уровней значительно мала по сравнению с энергиями отдачи ядра-излучателя или ядра-поглотителя.     Мессбауэр, исследуя явление резонансного поглощения γ‑квантов, понизил температуру источника и обнаружил, что число поглощенных фотонов существенно увеличилось. Он объяснил это тем, что ядро-излучатель и ядро-поглотитель не были свободными ядрами, а находились в кристаллах. В кристалле импульс отдачи, полученный отдельным ядром, сложным образом перераспределяется между соседними ядрами. А с уменьшением температуры кристалла и уменьшением энергии отдачи увеличивается относительное число ядерных переходов с передачей импульса отдачи всему кристаллу. Эффект Мессбауэра нашел многочисленные применения в разных областях науки. Например, с помощью эффекта Мессбауэра были измерены ширины уровней мессбауэровских ядер, было проверено соотношение неопределенностей, была измерена зависимость энергии фотона от высоты источника за счет силы тяжести. Расшифровка мессбауэровских спектров позволяет идентифицировать химический состав и выявить особенности кристаллических структур веществ. Литература Мухин К.Н. Экспериментальная ядерная физика. Книга 1, часть 1. // М., Энергоамтоиздат, 1993. Широков Ю.М., Юдин Н.П. Ядерная физика. // М., «Наука», 1980. Фабричный П.Б., Похолок, К.В. Мессбауэровская спектроскопия и ее применение для химической диагностики неорганических материалов. // Курс лекций для студентов и аспирантов хим. факультета МГУ, 2012. www.chem.msu.ru/rus/teaching/radio/fabrichn2012.pdf Эффект Мессбауэра // Википедия, https://ru.wikipedia.org/wiki/Эффект_Мессбауэра