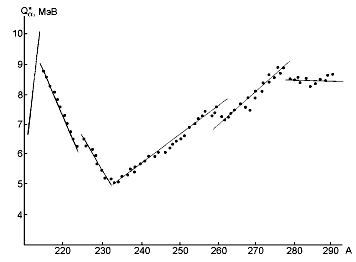
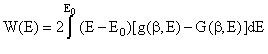В последние годы был достигнут
значительный прогресс в изучении сверхтяжелых
ядер; были синтезированы изотопы элементов с
порядковыми номерами от Z = 110 до Z = 118 [56 -65]. При
этом особую роль сыграли эксперименты
проведенные в ОИЯИ в Дубне, где в качестве
бомбардирующей частицы использовался изотоп 48Са,
содержащий большой избыток нейтронов [56-62], Это
позволило синтезировать нуклиды более близкие к
линии бета-стабильности и поэтому более
долгоживущие и распадающиеся с меньшей энергией.
Трудности, однако в том, что цепочка альфа
распада образующихся в результате облучения
ядер не заканчивается на известных ядрах и
поэтому идентификация образующихся продуктов
реакции, особенно их массового числа не
однозначна. В связи с этим, а также для понимания
свойств сверхтяжелых ядер, находящихся на
границе существования элементов необходимо
сопоставление результатов экспериментальных
измерений с теоретическими моделями.
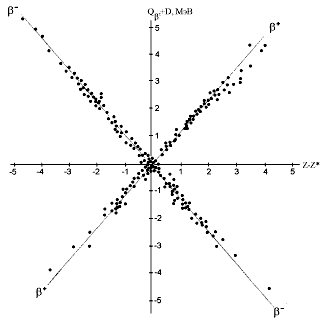
Ориентацию могла бы дать систематика
энергий  - и - и 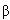 -распада,
учитывающая новые данные по трансфермиевым
элементам. Однако опубликованные до настоящего
времени работы [88-91] основывались на довольно
старых экспериментальных данных почти
двадцатилетней давности и поэтому оказываются
мало полезными. -распада,
учитывающая новые данные по трансфермиевым
элементам. Однако опубликованные до настоящего
времени работы [88-91] основывались на довольно
старых экспериментальных данных почти
двадцатилетней давности и поэтому оказываются
мало полезными.
Что касается теоретических работ, то
следует признать, что их выводы далеко не
однозначны. Прежде всего это зависит от того
какая выбрана теоретическая модель ядра (для
области трансфермиевых ядер наиболее
приемлемыми считаются макро-микро модель, метод
Скирма-Хартри-Фока и модель релятивистского
среднего поля). Но даже в рамках одной и той же
модели результаты зависят от выбора параметров и
от включения тех или иных поправочных членов.
Соответственно повышенная стабильность
прогнозируется при ( и вблизи) различных
магических числах протонов и нейтронов.
Так Мёллер [72] и некоторые другие
теоретики [73,74] пришли к заключению, что кроме
общеизвестных магических чисел (Z, N = 2, 8, 20, 28,
50, 82 и N = 126) должно проявляться как
магическое еще число Z = 114 в области
трансфермиевых элементов, а вблизи Z = 114 и N = 184
должен существовать остров относительно
стабильных ядер ( некоторые экзальтированные
популяризаторы поспешили пофантазировать по
поводу новых якобы стабильных сверхтяжелых ядер
и о связанных с ними новых источниках энергии).
Однако на деле в работах других авторов [75-79]
магичность Z = 114 отвергается и вместо этого
магическими числами протонов объявляются Z = 126
или 124.
С другой стороны в работах [80],[81]
утверждается, что магическими являются числа N =
162 и Z = 108. Однако с этим не согласны авторы работы
[82]. Расходятся мнения теоретиков и относительно
того должны ли ядра с числами Z = 114, N = 184 и с
числами Z = 108, N = 162 быть cферически-симметричными
или же они могут быть деформированными.
Что касается экспериментальной
проверки теоретических предсказаний о
магичности числа протонов Z = 114, то в
экспериментально достигнутой области с числами
нейтронов от 170 до 176 выделенности изотопов 114
элемента (в смысле их большей стабильности ) по
сравнению с изотопами других элементов
визуально не наблюдается .
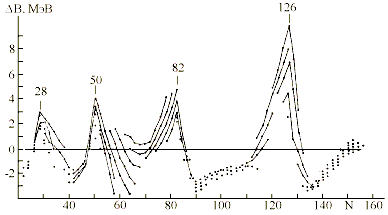
Сказанное иллюстрируется на 7, 8 и 9. На
рис 7, 8 и 9 кроме экспериментальных значений
энергий альфа-распада Qa трансфермиевых
ядер, нанесенных точками, показаны в виде кривых
линий результаты теоретических расчетов. На рис.7
приводятся результаты расчетов по макро-микро
модели работы [29], для элементов с четными Z,
найденные с учетом мультипольности деформаций
до восьмого порядка.
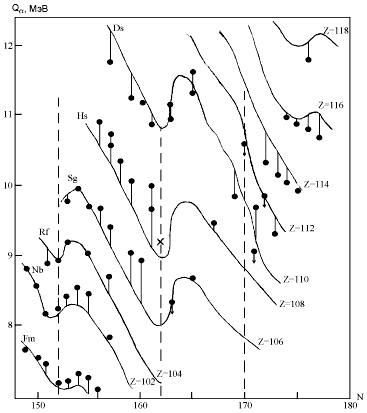
Рис.7. Сравнение результатов расчетов Qa
работы [29] с экспериментом [56-66]. |
На рис. 8 и 9 представлены
результаты расчетов Qa по оптимальной
формуле [45] для, соответственно, четных и нечетных
элементов. Отметим, что в [29] параметризация
производилась с учетом экспериментов,
выполненных 5-10 лет назад, тогда как в [45]
параметры не корректировались с момента
опубликования работы.
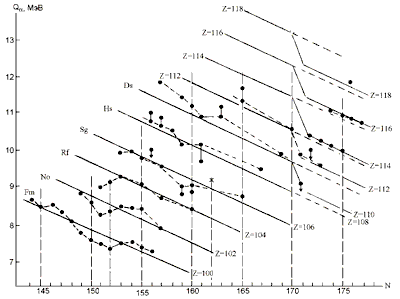
Рис. 8. Сравнение расчетов Qa по
"оптимальной" формуле (см. [45]) с
экспериментом [56-66] для ядер с четным Z > 100. |
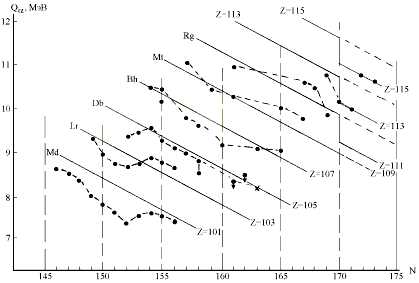
Рис. 9. Сравнение расчетов Qa по
"оптимальной" формуле (см. [45]) с
экспериментом [56-66] для ядер с нечетным Z > 100. |
Общий характер описания
трансфермиевых ядер ( с Z > 100) в [29] и [45]
примерно одинаков - среднеквадратичное
отклонение  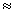 0,3 МэВ, однако в [29] для
ядер с N > 170 ход зависимости кривой Qa(N)
отличается от экспериментальной тогда как в [45]
достигается полное соответствие, если учесть
существование подоболочки N = 170. 0,3 МэВ, однако в [29] для
ядер с N > 170 ход зависимости кривой Qa(N)
отличается от экспериментальной тогда как в [45]
достигается полное соответствие, если учесть
существование подоболочки N = 170.
Следует констатировать, что
массовые формулы в ряде опубликованных в
последние годы работ [30-35] дают также достаточно
хорошее описание энергий Qa для ядер
трансфермиевой области (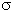 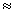 0,3-0,5 МэВ), а
в работе [30] расхождение в Qa для цепочки
самых тяжелых ядер 294118 0,3-0,5 МэВ), а
в работе [30] расхождение в Qa для цепочки
самых тяжелых ядер 294118  290116 290116  286114
оказывается в пределах экспериментальных ошибок
( правда для всей области трансфермиевых ядер 286114
оказывается в пределах экспериментальных ошибок
( правда для всей области трансфермиевых ядер 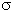  0,5
МэВ, т.е хуже, чем, например, в [29]). 0,5
МэВ, т.е хуже, чем, например, в [29]).
Выше в разделе 5.был описан простой
метод вычисления энергий альфа-распада ядер с
Z>82, основанный на использовании зависимости
энергии альфа-распада Qa ядра (А,Z) от
расстояния от линии бета-стабильности Z-Z*,
которая выражается формулами (22,23).Необходимые
для расчета Qa(A,Z) значения Z* находятся
по формуле (15), а Qa* -из рис.6 или по
формулам (17-21). Для всех ядер с Z>82, N>126 точность
расчета энергий альфа распада оказывается  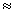 0,2
МэВ, т.е. по крайней мере не хуже, чем для массовых
формул глобального типа. Это иллюстрируется в табл. 1, где сопоставляются
результаты расчета Qa по формулам (22,23) с
экспериментальными данными, содержащимися в
таблицах изотопов [66]. Кроме того, в табл. 2 приводятся результаты
расчетов Qa для ядер с Z > 104
расхождения которых с недавними экспериментами
[56-64] остается в пределах тех же 0,2 МэВ. 0,2
МэВ, т.е. по крайней мере не хуже, чем для массовых
формул глобального типа. Это иллюстрируется в табл. 1, где сопоставляются
результаты расчета Qa по формулам (22,23) с
экспериментальными данными, содержащимися в
таблицах изотопов [66]. Кроме того, в табл. 2 приводятся результаты
расчетов Qa для ядер с Z > 104
расхождения которых с недавними экспериментами
[56-64] остается в пределах тех же 0,2 МэВ.
Что касается магичности числа Z = 108, то
как видно из рис.7, 8 и 9, существенного эффекта
повышения стабильности при этом числе протонов
не происходит. О том, наcколько значителен эффект
оболочки N = 162, в настоящее время судить трудно
ввиду отсутствия надежных экспериментальных
данных. Правда в работе Дворжака и др.[67] с помощью
радиохимического метода был выделен продукт,
распадающийся путем испускания альфа частиц с
довольно большим временем жизни и сравнительно
малой энергией распада, который был отождествлен
с ядром 270Hs с числом нейтронов N = 162
(соответствующее значение Qa на рис. 7 и 8
помечено крестиком). Однако результаты этой
работы расходятся с выводами других авторов [68-71].
Таким образом можно констатировать,
что пока нет серьезных оснований утверждать о
существовании в области тяжелых и сверхтяжелых
ядер новых магических чисел и связанного с ними
повышения стабильности ядер кроме установленных
ранее подоболочек N = 152 и Z =100. Что касается
магического числа Z =114, то, конечно, нельзя
полностью исключить (хотя это не представляется
весьма вероятным), что эффект оболочки Z =114 вблизи
центра острова стабильности (т.е.вблизи N = 184) мог
бы оказаться значительным, Однако эта область
пока что недоступна для экспериментального
изучения.
Для нахождения субмагических чисел и
связанных с ними эффектов заполнения
подоболочек логичным представляется метод
описаный в разделе 4. Как было показано в [52,53] (см.
выше - раздел 4), можно выделить области системы
ядер, внутри которых энергии связи нейтронов Bn
и энергии связи протонов Bp меняются
линейным образом в зависимости от числа
нейтронов N и числа протонов Z, а всю систему ядер
разбить на междумагические области, внутри
которых справедливы формулы (13) и (14).
(Суб)магическим числом можно назвать границу
между двумя областями регулярного (линейного)
изменения Bn и Bp, а под эффектом
заполнения нейтронной (протонной) оболочки–
понимать разность энергий Bn ( Bp) при
переходе из одной области в другую.
Субмагические числа заранее не задаются, а
находятся в результате согласования с
экспериментальными данными линейных формул (11) и
(12) для Bn и Bp при разбиения системы
ядер на области, см раздел 4, а также [53,83].
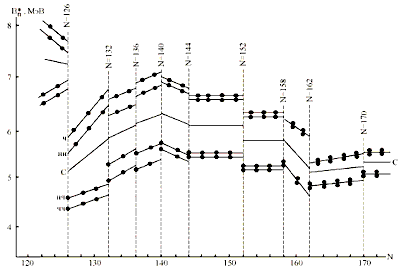
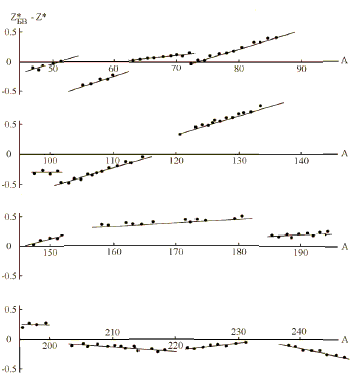
Рис.10. Приведенные (на линию бета-стабильности)
энергии связи нейтронов. |
Как видно из формул (11) и (12), Bn
и Bp являются функциями Z и N. Чтобы получить
представление о том, как меняется Bn в
зависимости от числа нейтронов и каков эффект
заполнения различных нейтронных (под)оболочек
оказывается удобным произвести приведение
энергий связи нейтронов на линию
бета-стабильности. Для этого при каждом
фиксированном значении N находилось Bn*
 Bn(N,Z*(N)), где
(согласно (15)) Z*(N) = 0,5528Z + 14,1. Зависимость Bn*
от N для ядер всех четырех типов четности
представлена на рис.10 для ядер с N > 126.
Каждая из точек на рис.10 соответствует среднему
значению приведенных на линию бета-стабильности
значений Bn* для ядер одной и той
четности с одним и тем же N. Bn(N,Z*(N)), где
(согласно (15)) Z*(N) = 0,5528Z + 14,1. Зависимость Bn*
от N для ядер всех четырех типов четности
представлена на рис.10 для ядер с N > 126.
Каждая из точек на рис.10 соответствует среднему
значению приведенных на линию бета-стабильности
значений Bn* для ядер одной и той
четности с одним и тем же N.
Как видно из рис.10, Bn* испытывает
скачки не только при общеизвестном магическом
числе N = 126 (падение на 2 МэВ) и при субмагическом
числе N = 152 (падение на 0,4 МэВ для ядер всех типов
четности ), но и при N = 132, 136, 140, 144, 158, 162, 170.Характер
этих подоболочек оказывается различным. Дело в
том, что величина и даже знак оболочечного
эффекта оказывается различным для ядер
различного типа четности. Так при переходе через
N = 132 Bn* понижается на 0,2 МэВ для ядер с
нечетными N, но на столько же повышается для ядер
с четными N . Средняя же по всем типам четности
энергия С (линия С на рис 10) разрыва не испытывает.
Рис. 10 позволяет проследить, что происходит
при пересечении других перечисленных выше
субмагических чисел. Существенно, что средняя
энергия С либо не испытывает разрыва, либо
меняется на ~0,1 МэВ в сторону убывания (при
N = 162), или возрастания (при N = 158 и
N = 170).
Общая тенденция изменения энергий Bn*такова:
после заполнения оболочки N =126 энергии связи
нейтронов растут до N =140, так, что средняя энергия
С достигает 6 МэВ, после чего она уменьшается
примерно на 1 МэВ у самых тяжелых ядер.
Аналогичным образом были найдены
энергии протонов, приведенных на линию
бета-стабильности Bp*  Bp(Z, N*(Z)) при учете
(следующей из (15)) формулы N*(Z) = 1,809N – 25,6.
Зависимость Bp* от Z представлена на
рис.11. По сравнению с нейтронами энергии связи
протонов испытывают более резкие колебания при
изменении числа протонов Как видно из рис.11,
энергии связи протонов Bp* испытывают
разрыв кроме главного магического числа Z = 82
(уменьшение Bp* на 1.6 МэВ) при Z = 100, а
также при субмагических числах 88, 92, 104, 110. Как и в
случае нейтронов пересечение протонных
субмагических чисел приводит к различным по
величине и знаку оболочечным эффектам. Среднее
значение энергии С не меняется при пересечении
числа Z = 104, но понижается на 0,25 МэВ при
пересечении чисел Z = 100 и 92 и на 0,15 МэВ при
Z = 88 и на столько же повышается при
Z = 110. Bp(Z, N*(Z)) при учете
(следующей из (15)) формулы N*(Z) = 1,809N – 25,6.
Зависимость Bp* от Z представлена на
рис.11. По сравнению с нейтронами энергии связи
протонов испытывают более резкие колебания при
изменении числа протонов Как видно из рис.11,
энергии связи протонов Bp* испытывают
разрыв кроме главного магического числа Z = 82
(уменьшение Bp* на 1.6 МэВ) при Z = 100, а
также при субмагических числах 88, 92, 104, 110. Как и в
случае нейтронов пересечение протонных
субмагических чисел приводит к различным по
величине и знаку оболочечным эффектам. Среднее
значение энергии С не меняется при пересечении
числа Z = 104, но понижается на 0,25 МэВ при
пересечении чисел Z = 100 и 92 и на 0,15 МэВ при
Z = 88 и на столько же повышается при
Z = 110.
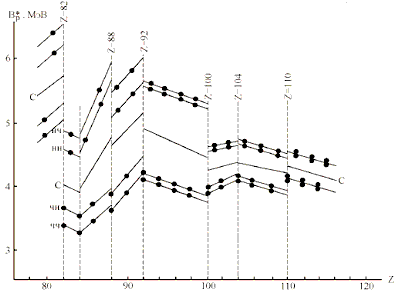
Рис.11. Приведенные (на линию бета-стабильности)
энергии связи протонов. |
На рис.11 прослеживается
общая тенденция изменения Bp* после
заполнения протонной оболочки Z = 82 -это рост до
урана (Z = 92) и постепенное спадание с оболочечными
колебаниями в области самых тяжелых элементов.
При этом среднее значение энергии меняется от 5
МэВ в области урана до 4 МэВ для самых тяжелых
элементов и вместе с этим уменьшается энергия
спаривания протонов.
Как следует из рис.10 и 11, в области
самых тяжелых элементов помимо общего
уменьшения энергий связи происходит ослабление
связи внешних нуклонов между собой, что
проявляется в уменьшении энергии спаривания
нейтронов и энергии спаривания протонов, а также
нейтрон-протонного взаимодействия. Это
демонстрируется в явном виде на рис.12.
Для ядер, лежащих на линии
бета-стабильности энергия спаривания нейтронов  nn определялась
как разность энергии четно(Z)-нечетного(N) ядра Bn*(N)
и полусуммы nn определялась
как разность энергии четно(Z)-нечетного(N) ядра Bn*(N)
и полусуммы
(Bn*(N-1) + Bn*(N+1))/2
для четно-четных ядер ; аналогично энергия
спаривания протонов 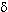 pp
находилась как разность энергии
нечетно-четного ядра Bр*(Z) и полусуммы
( Bp*(Z-1) + Bp*(Z+1))/2 для
четно-четных ядер. Наконец, энергия
np-взаимодействия pp
находилась как разность энергии
нечетно-четного ядра Bр*(Z) и полусуммы
( Bp*(Z-1) + Bp*(Z+1))/2 для
четно-четных ядер. Наконец, энергия
np-взаимодействия 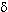 np
находилась как разность Bn*(N)
четно-нечетного ядра и Bn*(N)
четно-четного ядра. np
находилась как разность Bn*(N)
четно-нечетного ядра и Bn*(N)
четно-четного ядра.
Рис.12. Энергии спаривания 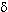 nn, nn, 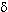 pp и pp и 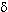 np Z > 82,
N > 126. np Z > 82,
N > 126. |
Рис.10,11 и 12 не дают, однако,
полного представления о том, как меняются
энергии связи нуклонов Bn и Bp (и все то,
что с ними связано) в зависимости от соотношения
между числами нейтронов и протонов. С учетом
этого в дополнение к рис. 10,11 и 12 в целях
наглядности приводится (в соответствии с
формулами (13) и (14)) рис.13, на котором представлена
пространственная картина энергий связи
нейтронов Bn как функции числа нейтронов N и
протонов Z.
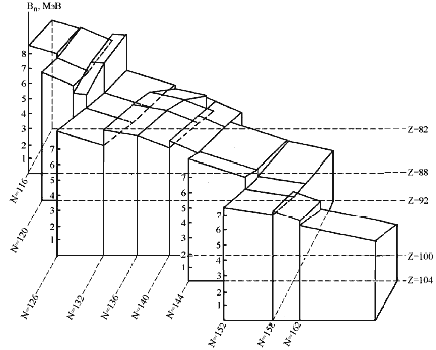
Рис. 13. Bn как функция Z и N. |
Отметим некоторые общие
закономерности , проявляющиеся при анализе
энергий связи ядер области Z>82, N>126, в том числе
на рис.13. Энергетическая поверхность B(Z,N)
непрерывна всюду, в том числе и на границах
областей. Энергия связи нейтронов Bn (Z,N),
меняющаяся линейно в каждой из междумагических
областей, испытывает разрыв только при
пересечении границы нейтронной (под)оболочки,
тогда как при пересечении протонной
(под)оболочки может измениться лишь наклон  Bn / Bn / Z. Z.
Наоборот Bр(Z,N) испытывает разрыв
только на границе протонной (под)оболочки, а на
границе нейтронной (под)оболочки может лишь
измениться наклон  Bр
/ Bр
/ N. В пределах
междумагической области Bn растет при
увеличении Z и медленно убывает при увеличении N;
аналогично Bр растет при увеличении N и
убывает при увеличении Z. При этом изменение Bр
происходит значительно быстрее, чем Bn. N. В пределах
междумагической области Bn растет при
увеличении Z и медленно убывает при увеличении N;
аналогично Bр растет при увеличении N и
убывает при увеличении Z. При этом изменение Bр
происходит значительно быстрее, чем Bn.
Численные значения Bр и Bn
приведены в табл. 3, а
значения определяющих их параметров, (см.формулы
(13) и (14)) - в табл 4. Значения n0нч
n0нн, а также р0чн и р0нн
в табл.1 не приводятся, но
они находятся как разности В*n для
нечетно-четных и четно-четных ядер и,
соответственно четно-четных и нечетно-нечетных
ядер на рис. 10 и как разности В*р для
четно-нечетных и четно-четных и соответственно
нечетно-четных и нечетно-нечетных ядер на рис.11.
Анализ оболочечных эффектов,
результаты которого представлены на рис 10-13
зависят от входных экспериментальных данных-
главным образом от энергий альфа- распада Qa
и изменение последних могло бы привести к
корректировке результатов этого анализа. Это в
особенности относится к области Z > 110,
N > 160, где иногда заключения делались на
основании одной единственной энергии
альфа-распада. Что касается области Z < 110,
N < 160, где результаты экспериментальных
измерений за последние годы практически
стабилизировались, то результаты анализа,
приведенные на рис. 10 и 11 практически
совпадают с теми, которые были получены в [85-87]
двадцать и более лет назад.
Настоящая работа представляет собой
обзор различных подходов к проблеме энергий
связи ядер с оценкой их достоинств и недостатков.
Работа содержит достаточно большой объем
информации о работах различных авторов.
Дополнительную информацию можно получить,
ознакомившись с оригинальными работами, многие
из которых процитированы в списке литературы
настоящего обзора, а также в материалах
конференций по массам ядер, в частности
конференций AF а МС (публикации в ADNDT № 13 и 17 и др.) и
конференциям по ядерной спектроскопии и
структуре ядра, проводящимся в России. Таблицы
настоящей работы содержат результаты
собственных оценок автора, относящиеся к
проблеме сверхтяжелых элементов (СТЭ).
Автор глубоко благодарен Б.С.Ишханову,
по предложению которого была подготовлена
настоящая работа, а также Ю.Ц.Оганесяну и
В.К.Утенкову за самую свежую информацию об
экспериментальных работах, проводимых в ЛЯР ОИЯИ
по проблеме СТЭ.
СПИСОК ЛИТЕРАТУРЫ
- N.Ishii,S.Aoki,T.Hatsidi, Nucl.Th./0611096.
- M.M.Nagels,J.A.Rijken,J.J.de Swart, Phys.Rev.D,17,768(1978).
- S.Machleidt,K.Hollande,C.Elsla,Phys.Rep.149,1(1987).
- M.Lacomb et al.Phys.Rev.C21,861(1980).
- V.G.Neudachin,N.P.Yudin et al.Phys.rEv.C43,2499(1991).
- R.B.Wiringa,V.Stoks,R.Schiavilla,Phys.Rev.C51,38(1995).
- R.V.Reid, Ann. Phys.50,411(1968).
- H.Eikemeier,H.Hackenbroich.Nucl.Phys/A169,407(1971).
- D.R.Thomson,M.Lemere,Y.C.Tang,Nucl.Phys.A286,53(1977).
- Н.Н.Колесников,В.И.Тарасов,ЯФ,35,609(1982).
- Г.Бете,Ф.Бечер, Физика ядра,ДНТВУ, 1938.
- J.Carlson,V.R.Pandharipande,R.B.Wiringa,Nucl.Phys.A401,59(1983).
- D.Vautherin,D.M.Brink,Phys.Rev.C5,629(1976).
- M.Beiner et al.Nucl.Phys.A238,29(1975).
- C.S.Pieper,R.B.Wiringa,Ann.Rev.Nucl.Part.Sci.51,53(2001).
- В.А.Кравцов, Массы атомов и энергии связи
ядер.Атомиздат.1974.
- М.Гепперт-Майер, И.Иенсен Элементарная теория
ядерных оболочек,ИИЛ, М-1958.
- W.Elsasser, J.Phys.rad.5,549(1933); Compt.Rend.199,1213(1934).
- K.Guggenheimer, J.Phys.rad. 2,253(1934).
- W.D.Myers,W.Swiatecki, Nucl.Phys.81,1(1966).
- В.М.Струтинский ,ЯФ, 3,614(1966).
- S.G.Nilsson.Kgl.Danske Vid.Selsk.Mat.Fys.Medd.29,N16,1(1955).
- W.D.Myers, ADNDT,17,412(1976); W.D.Myers,W.J/Swiatecki, Ann.Phys.55,395(1969).
- H.v.Groot,E.R.Hilf,K.Takahashi,ADNDT,17,418(1976).
- P.A.Seeger,W.M.Howard, Nucl.Phys.A238,491(1975).
- J.Janecke, Nucl.Phys.A182,49(1978).
- P.Moller, J.R.Nix, Nucl.Phys.A361,49(1978)
- M.Brack et al. Rev.Mod.Phys.44,320(1972).
- R.Smolenczuk, Phys.Rev.C56.812(1997); R.Smolenczuk, A.Sobicziewsky,
Phys.Rev.C36,812(1997).
- I.Muntian et al.Phys.At.Nucl.66,1015(2003).
- A.Baran et al.Phys.Rev.C72,044310(2005).
- S.Gorely et al.Phys.Rev.C66,034313(2002).
- S.Typel,B.A.Brown,Phys.Rev.C67,034313(2003).
- S.Cwiok et al.Phys.Rev.Lett.83,1108(1999).
- V.Render, Phys.Rev.C61,031302®(2002).
- D.Vautherin,D.M.BrikePhys.Rev.C5,626(1979).
- K.T.Davies et al.Phys.Rev.177,1519(1969).
- A.K.Herman et al.Phys.Rev.147,710(1966).
- R.J.Mc.Carty,K.Dover, Phys.Rev.C1,1644(1970).
- K.A Brueckner,J.L.Gammel,H.WeitznerPhys.Rev.110,431(1958).
- K Hollinder et al.Nucl.Phys.A194,161(1972).
- M.Yamada. Progr.Theor.Phys.32,512.(1979).
- V.Bauer,ADNDT,17,462((1976).
- M.Beiner,B.J.Lombard,D.Mos, ADNDT,17,450(1976).
- Н.Н.Колесников,В.М.Вымятнин. ЯФ.31,79 (1980).
- G.T.Garvey,I.Ktlson, Phys.Rev.Lett.17,197(1966).
- E.Comey,I.Kelson, ADNDT,17,463(1976).
- I.Talmi,A.de Shalit, Phys.Rev.108.378(1958).
- I.Talmi,R.Thiberger,Phys.Rev.103,118(1956).
- A.B.Levy, Phys,Rev.106,1265(1957).
- Н.Н,Колесников, ЖЭТФ, 30,889(1956).
- Н.Н.Колесников, Вестник МГУ, № 6,76(1966).
- Н.Н.Колесников, Изв.АН СССР,сер.физ.,49,2144(1985).
- N.Zeldes. Shell model interpretation of nuclear masses. The Racah institute of physics,
Jerusalem,1992.
- S.Liran,N.Zeldes, ADNDT,17,431(1976).
- Yu.Ts.Oganessian et al.Phys.Rev.C74,044602(2006).
- Yu.Ts.Oganessian et al.Phys.Rev.C69,054607(2004); Препринт ОИЯИ
Е7-2004-160.
- Yu.Ts.Ogantssian et al.Phys.Rev.C62,041604®(2000)
- Yu.Ts.Oganessian et al.Phts.Rev.C63,0113301®,(2001).
- S.Hofmann,G.Munzenberg,Rev.Mod.Phys.72,733(2000).
- S.Hofmann et al.Zs.Phys.A354,229(1996).
- Yu.A.Lazarev et al. Phys.Rev.C54,620(1996).
- A.Ghiorso et al.Phys.Rev.C51,R2298(1995).
- G.Munzenberg et al.Zs.Phys.A217,235(1984).
- P.A.Vilk et al. Phys.Rev.Lett.85,2697(2000).
- Tables of isotopes.8-th.ed.,R.B.Firestone et al. New York,1996.
- J.Dvorak et al Phys.Rev.Lett.97,942501(2006).
- S.Hofmann et al.Eur.Phys.J.A14,147(2002).
- Yu.A.Lazarevet al.Phys.Rev.Lett.73,624(1996).
- A.Ghiorso et al.Phys.Lett.B82,95(1976).
- A.Turleret al.Phys.Rev.C57,1648(1998).
- P.Moller,J.Nix,J.Phys.G20,1681(1994).
- W.D.Myers,,W.Swiatecki,Nucl.Phys.A601,141(1996).
- A.Sobicziewsky,Acta Phys.Pol.B29,2191(1998).
- J.B.Moss,Phys.Rev.C17,813(1978).
- F.Petrovich et al.Phys.Rev.Lett.37,558(1976).
- S.Cwiok et al Nucl.Phys.A611,211(1996).
- K.Rutz et al.Phys.Rev.C56,238(1997).
- A.Kruppa et al.Nucl,Phys.C61,034313(2000).
- Z.Patyk et al.Nucl.Phys.A502,591(1989).
- M.Bender et al. Rev.Vod.Phys.75,21(2002).
- P.Moller et al.Nucl.Phys.A469,1(1987).
- J.Carlson, R.Schiavilla. Rev.Mod.Phys.70,743(1998).
- V.I.Goldansky.Nucl.Phys.A133,438(1969).
- Н.Н.Колесников, А.Г.Демин. СообщениеОИЯИ,Р6-9420(1975).
- Н.Н.Колесников, А.Г.Демин.ВИНИТИ, №7309-887(1987).
- Н.Н.Колесников, ВИНИТИ. №4867-80(1980).
- V.E.Viola, A.Swart, J.Grober. ADNDT,13,35.(1976).
- A.HWapstra, G.Audi, Nucl.Phys.A432,55.(1985).
- K.Takahashi, H.v.Groot. AMFC.5,250(1976).
- R.A.Glass, G.Thompson, G.T.Seaborg. J.Inorg. Nucl.Chem. 1,3(1955).
|
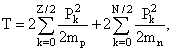
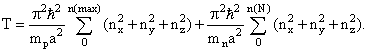
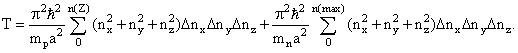
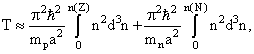
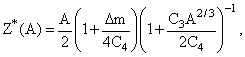
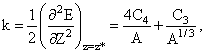 откуда
видно, что изобарное сечение ядерной
энергетической поверхности представляет собой
квадратичную параболу.
откуда
видно, что изобарное сечение ядерной
энергетической поверхности представляет собой
квадратичную параболу. 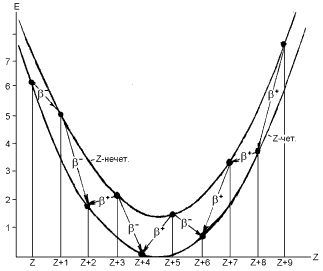
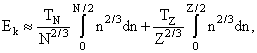
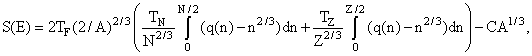
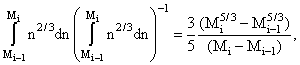
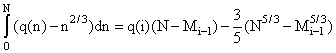 при Mi-1 < N < Mi.
при Mi-1 < N < Mi.
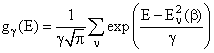 ,
,