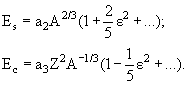Тема 1. Свойства атомных ядер

    Перечислим основные характеристики ядер, которые будут обсуждаться далее:

1. Энергия связи и массы ядер.
2. Размеры ядер.
3. Спин ядра и моменты импульсов составляющих ядро нуклонов.
4. Четность ядра и частиц.
5. Изоспин ядра и нуклонов.
6. Спектры ядер. Характеристики основного и возбужденных состояний.
7. Электромагнитные свойства ядра и нуклонов.

1. Энергии связи и массы ядер

    Масса стабильных ядер меньше суммы масс входящих в ядро нуклонов, разность этих величин и определяет энергию связи ядра:

В (1.1) M_N(A,Z) – масса ядра, Z – число протонов в ядре, А – число нуклонов. Однако в таблицах масс приводятся, как правило, не массы ядер, а массы нейтральных атомов либо величины «избытков масс» Δ = M – A, где М – масса нейтрального атома в МэВ. Это связано, в первую очередь, с методикой измерения масс с помощью масс-спектрометров.

Часто массы нейтральных атомов приводят в единицах

(1.2)

    В банке ядерных данных www.nndc.bnl.gov собраны значения «избытков масс» Δ = M – A (см. также приложение к сборнику задач «Субатомная физика», изд. МГУ, 1994 и банк данных об основных состояниях ядер cdfe.sinp.msu.ru/services/gsp.en.html). Величина А представляет собой в данном случае произведение числа нуклонов на значение единицы массы (1.2) в МэВ. Таким образом, величины Δ приводятся в единицах МэВ, что удобно для проведения расчетов.

    Для примера вычислим величину энергии связи и удельной энергии связи ядра ¹²С двумя способами:
а) пользуясь таблицей масс в единицах (1.1) и
б) используя таблицу избытков масс Δ = M – A.
    Прежде всего, необходимо преобразовать формулу (1.1), заменив массы ядер M_N на массы нейтральных атомов М:

 Формула (1.3) является приближенной – в ней опущены энергии связи электронов в атомах. Однако поскольку энергии связи нуклонов в ядре на 5 – 6 порядков превышают энергии связи электронов в атомах, это приближение не скажется на точности дальнейших расчетов энергий связи ядер. Прибавляя и вычитая Zm_e в (1.3), получим для энергии связи нуклонов в ядрах

Для ядра ¹²С по первому способу

E_св = [6·1.007825 + 6·1.008665 – 12.00000]×931.5 МэВ

Для использования таблиц для Δ = M – A преобразуем (1.4)

Для энергии связи ¹²С расчет этим способом проще:

E_св = 6·7.289 МэВ + 6·8.071 – 0 = 92.16 МэВ.

    Поэтому в дальнейших расчетах будет использоваться именно второй способ, основанный на таблицах для избытков масс Δ = M – A.
    Удельная энергия связи, т.е. энергия связи на один нуклон, для ядра ¹²С составляет

(1.6)

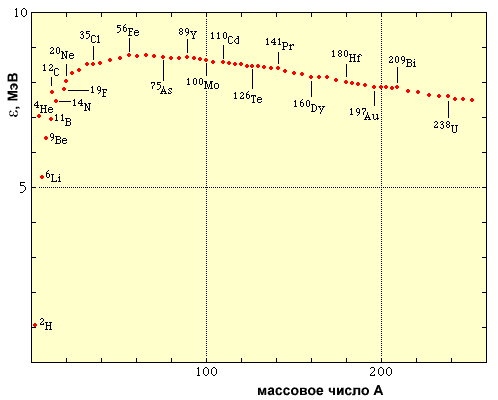
Зависимость удельной энергии связи от числа нуклонов А является наиболее важным для приложений экспериментальным результатом физики ядра (рис.1.1).

    Экспериментально установленное распределение удельных энергий связи ядер по значениям чисел нуклонов в ядре А имеет следующие характерные черты:

1. В широкой области ядер удельная энергия связи ε слабо зависит от А;
2. Для ядер с малыми А удельная энергия имеет «спад».
3. Для тяжелых ядер средняя удельная энергия связи меньше, чем для средних, причем с ростом А наблюдается снижение ее величины.
4. Для ядер с Z = N удельная энергия выше, чем для других ядер с тем же значением А.
5. Четно-четные (по Z и N) ядра  имеют в среднем большие значения ε, чем нечетно-четные, а нечетно-нечетные – меньшие.

    Теоретическое объяснение этого распределения дает модель заряженной жидкой капли и соответствующая этой модели формула Вайцзеккера.
    Первая из перечисленных (и главная) особенность распределения удельных энергий связи ядер – следствие насыщения ядерных сил и их короткого радиуса действия.
    Вторая связана с тем, что связи нуклонов, находящихся на поверхности ядра, с другими нуклонами ядра не полностью насыщены. Чем больший процент нуклонов находится на поверхности ядра, тем больше «убыль» энергии насыщения (этими особенностями ядерные силы оказываются подобны силам, действующим между молекулами жидкости).
    Третья особенность распределения удельной энергии связи объясняется тем, что протоны ядер участвуют не только в сильном (ядерном), но и в электромагнитном взаимодействии. Чем больше протонов, тем выше энергия кулоновского отталкивания.
    Четвертая и пятая особенности распределения – следствия оболочечной структуры ядра и симметрии, связанной с реализацией в ядре принципа Паули.
    Учет всех перечисленных свойств приводит к полуэмпирической формуле Вайцзеккера или модели заряженной жидкой капли (von Weizsäcker, 1935):

(1.7)

    Коэффициенты в (1.7) подбираются из условий наилучшего совпадения кривой  модельного распределения с экспериментальными данными. Поскольку такая процедура может быть проведена по-разному, существует несколько наборов коэффициентов формулы Вайцзеккера. Часто используются в (1.7) следующие:

a₁ = 15.6 МэВ, a₂ = 17.2 МэВ, a₃ = 0.72 МэВ, a₄ = 23.6 МэВ,

    Несложно оценить значение зарядового числа Z, при котором ядра становятся нестабильными по отношению к спонтанному распаду.
    Спонтанный распад ядра возникает в случае, если кулоновское расталкивание протонов ядра начинает преобладать над стягивающими ядро ядерными силами. Оценка ядерных параметров, при которых наступает такая ситуация, может быть проведена из рассмотрения изменений в поверхностной и кулоновской энергиях при деформации ядра. Если деформация приводит к более выгодному энергетически состоянию, ядро будет спонтанно деформироваться вплоть до деления на два фрагмента. Количественно такая оценка может быть проведена следующим образом.
    При деформации ядро, не меняя своего объема, превращается в эллипсоид с осями (см. рис. 1.2):

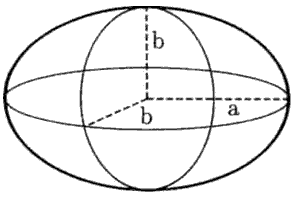
    При деформации первый член формулы (1.7) не меняется, второй (поверхностная энергия) E_s - по абсолютной величине возрастает, а третий (кулоновская энергии) E_c - уменьшается:

(1.8)

Таким образом, деформация изменяет полную энергию ядра на величину

(1.9)

Здесь учтен знак (-) второго и третьего членов в (1.7).

    Если величина изменения энергии (1.9) положительна, энергия связи ядра будет расти, т.е. деформация будет энергетически выгодна, и спонтанное деление возможно. Спонтанное деление неизбежно, когда значения (1.9) становятся больше нуля, т.е. при значениях

(1.10)

    Следует подчеркнуть приближенный характер полученного результата как следствия классического подхода к квантовой системе – ядру.

2. Энергии отделения нуклонов и кластеров от ядра

    Энергия отделения нейтрона от ядра равна

E_отд.n = M(A–1,Z) + m_n – M(A,Z) = Δ(A–1,Z) + Δ_n – Δ(A,Z).

    Энергия отделения протона

E_отд.p = M(A–1,Z–1) + M(¹H) – M(A,Z) = Δ(A–1,Z–1) + Δ(¹H) – Δ(A,Z).

    Следует отметить, что поскольку основными данными о массах ядер являются таблицы «избытков» масс Δ, расчеты энергий отделения удобнее проводить с помощью этих величин.

E_отд.n(¹²C) = Δ(¹¹C) + Δ_n – Δ(¹²C) = 10.65 МэВ + 8.07 МэВ – 0 = 18.72 МэВ.

E_отд.α = M(A–4,Z–2) + M(⁴He) – M(A,Z) = Δ(A–4,Z–2) + Δ(⁴He) – Δ(A,Z).

E_отд.α(¹²C) = Δ(⁸Be) + Δ(⁴He) – Δ(¹²C) = (4.941 + 2.424 – 0) МэВ = 7.365 МэВ.

    Сравним результаты, полученные для удельной энергии связи ядра ¹²С и энергий отделения от него нейтрона и протона.
    Энергия отделения одного нуклона от этого ядра оказалась вдвое выше удельной энергии связи! Энергия одновременного отделения кластера из 4 нуклонов - α-частицы оказалась меньше удельной энергии связи – т.е. средней энергии отделения одного нуклона. Эти факты и аналогичные результаты для ряда других ядер были объяснены в теоретических моделях ядер. Аналогичные расчеты для ядер ¹¹B, ¹³С, ¹³N, ¹⁴С показывают, что ядро ¹²С обладает особой устойчивостью по сравнению с соседними (по А) ядрами. Эти результаты сведены в Таблицу 1.