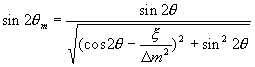|
Н. Машутиков
Осцилляции нейтрино
Теория нейтринных осцилляций появилась как возможное
решение проблемы дефицита солнечных нейтрино. Суть проблемы заключалась в том,
что на солнце, в соответствии со стандартной моделью, нейтрино в основном
возникают в результате реакции протон-протонного цикла:
p + p  2H + e+ +
2H + e+ +  e
+ 0.42 МэВ e
+ 0.42 МэВ
(Относительная вероятность такой реакции 99.75%)
Главным источником высокоэнергетичных нейтрино на Солнце
служат 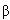 -распады
изотопов
8B, которые возникают в реакции 7Be(p, -распады
изотопов
8B, которые возникают в реакции 7Be(p, )8B
(редкой ветви протон - протонного цикла): )8B
(редкой ветви протон - протонного цикла):
8B 8Be+ 8Be+ e e
Далее по вероятности образования идут нейтрино СNO – цикла:
13N  13C + e+ +
13C + e+ +  e
+ 1.20 МэВ e
+ 1.20 МэВ
15O  15N + e+ +
15N + e+ +  e
+ 1.73 МэВ e
+ 1.73 МэВ
В настоящее время имеются четыре серии экспериментальных
данных по регистрации различных групп солнечных нейтрино. В течение 30 лет
ведутся радиохимические эксперименты на основе реакции 37Cl +  e e 37Ar
+ e-.
Согласно теории, основной вклад в эту реакцию должны внести нейтрино от распада
8В. Исследования по прямой регистрации нейтрино от распада 8В с
измерением энергии и направления движения нейтрино выполняются в эксперименте
KAMIOKANDE с 1987 года. Радиохимические эксперименты по реакции 71Ga
+ 37Ar
+ e-.
Согласно теории, основной вклад в эту реакцию должны внести нейтрино от распада
8В. Исследования по прямой регистрации нейтрино от распада 8В с
измерением энергии и направления движения нейтрино выполняются в эксперименте
KAMIOKANDE с 1987 года. Радиохимические эксперименты по реакции 71Ga
+  e e 71Ge + e-
ведутся последние пять лет двумя группами ученых ряда стран. Важной особенностью
этой реакции является ее чувствительность в основном к первой реакции
протон-протонного цикла p + p 71Ge + e-
ведутся последние пять лет двумя группами ученых ряда стран. Важной особенностью
этой реакции является ее чувствительность в основном к первой реакции
протон-протонного цикла p + p  2D
+ e+ + 2D
+ e+ +  e.
Темп этой реакции определяет скорость энерговыделения в термоядерной печи Солнца
в реальном масштабе времени. Во всех экспериментах наблюдается дефицит в потоках
солнечных нейтрино по сравнению с предсказаниями Стандартной солнечной модели. e.
Темп этой реакции определяет скорость энерговыделения в термоядерной печи Солнца
в реальном масштабе времени. Во всех экспериментах наблюдается дефицит в потоках
солнечных нейтрино по сравнению с предсказаниями Стандартной солнечной модели.
Возможным решением проблемы дефицита солнечных нейтрино
являются нейтринные осцилляции - превращение электронных нейтрино в мюонные и
тау-нейтрино.
Первое, на что надо обратить внимание, приступая к обсуждению
свойств нейтрино, это существование их различных сортов.
Как известно , в настоящее время мы определенно можем
говорить о трех таких сортах:
νe, νμ, ντ и соответственно их антинейтрино.
Электронное нейтрино при обмене заряженным W-бозоном переходит в электрон, а
мюонное - в мюон ( ντ
производит тау-лептон). Это свойство и позволило в свое время установить
различие в природе электронного и мюонного нейтрино. А именно, нейтринные пучки,
формируемые на ускорителях, состоят в основном из продуктов распада заряженных π-мезонов:
π+  μ+ + ν μ+ + ν
π−  μ− + ν μ− + ν
Если нейтрино не различает сорта лептонов, то полученные таким образом
нейтрино с равной вероятностью будут производить электроны и мюоны при
взаимодействии с ядрами вещества. Если каждому лептону соответствует свой сорт
нейтрино, то в распадах пионов порождаются только мюонные его сорта. Тогда
нейтринный пучок от ускорителя будет в подавляющем числе случаев давать мюоны, а
не электроны. Именно такое явление и было зарегистрировано на эксперименте.
После выяснения факта различия сортов нейтрино возник вопрос:
насколько глубоким является это различие? Если обратиться к аналогии с кварками,
то следует обратить внимание на то, что электрослабые взаимодействия не
сохраняют сорт (аромат) кварков . Возможна, например, следующая цепочка
переходов:
s  u + W-
u + W-  d d
что приводит к смешиванию состояний, отличающихся только странностью,
например, нейтральных K-мезонов K0 и
K0.
Могут ли аналогичным образом смешиваться и разные сорта нейтрино? При ответе на
этот вопрос важно знать, каковы массы нейтрино. Из наблюдений мы знаем, что
нейтрино имеют массы очень маленькие, существенно меньше, чем массы
соответствующих лептонов. Так, для массы электронного нейтрино мы имеем
ограничение
m ( e) < 5.1
эВ, e) < 5.1
эВ, |
(1) |
в то время как масса электрона равна 0.51099906 ± 0.00000015 МэВ
В подавляющем большинстве случаев мы можем полагать массы
всех трех нейтрино равными нулю. Если они в точности равны нулю, заметить
эффекты возможного смешивания различных сортов нейтрино невозможно. Только если
нейтрино имеют отличные от нуля массы, смешивание приобретает физический смысл.
Отметим, что нам неизвестны какие-либо принципиальные причины, приводящие к
строгому равенству нулю масс нейтрино. Таким образом, вопрос о том, существует
ли смешивание разных нейтрино, представляет собой задачу, которую следует решать
физическими методами, прежде всего экспериментальными. Впервые на возможность
смешивания электронного и мюонного сортов нейтрино указал Б.М. Понтекорво.
Смешивание нейтринных состояний
Рассмотрим задачу о двух сортах нейтрино:  e,
νμ ,. Для эффектов смешивания следует рассмотреть, как развиваются
состояния в зависимости от времени. Эволюцию во времени определяет уравнение
Шредингера e,
νμ ,. Для эффектов смешивания следует рассмотреть, как развиваются
состояния в зависимости от времени. Эволюцию во времени определяет уравнение
Шредингера
i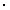 dФ/dt = HФ. dФ/dt = HФ. |
(2) |
Здесь H - энергия системы (точнее, оператор энергии). Для
состояния с определенной энергией зависимость от времени прямо следует из (2):
|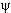 (t)>
= eiEt
| (t)>
= eiEt
|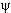 (0)>. (0)>. |
(3) |
С этого места мы используем систему единиц h = c = 1,
которая обычно употребляется в физике элементарных частиц. Эта система удобна
тем, что в ней имеется всего лишь одна размерная величина, например энергия.
Одинаковые размерности с энергией имеют теперь импульс и масса, а координата x и
время t имеют размерность обратной энергии . Применяя это соотношение к
рассматриваемому нами случаю нейтрино, когда их массы много меньше импульса,
получаем вместо (2):
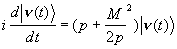 . .
|
(4) |
Теперь мы предполагаем, что нейтрино мюонные и электронные могут переходить
друг в друга, поэтому волновая функция есть смесь двух состояний
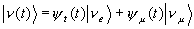
|
(5) |
Исходя из (5) мы понимаем уравнение (4) как систему уравнений на функции 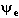 (t), (t), 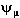 (t): (t):
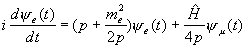
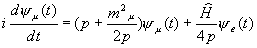
|
(6) |
Для краткости обычно такую систему записывают в виде (4), но понимают тогда  (t) как столбец
из (t) как столбец
из 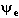 , , 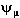 ,
а в скобках первый член пропорционален единичной матрице, в то время как
величина M2
становится некоторой (2 x 2)-матрицей с матричными элементами, которые легко
получить из системы (6). Здесь очень важна величина ,
а в скобках первый член пропорционален единичной матрице, в то время как
величина M2
становится некоторой (2 x 2)-матрицей с матричными элементами, которые легко
получить из системы (6). Здесь очень важна величина  , отличие которой от нуля и приводит к
эффектам смешивания. Если ее нет, система распадается на два независимых
уравнения и нейтрино, электронное и мюонное, раздельно существуют со своими
собственными массами. , отличие которой от нуля и приводит к
эффектам смешивания. Если ее нет, система распадается на два независимых
уравнения и нейтрино, электронное и мюонное, раздельно существуют со своими
собственными массами.
Итак, H 0. Тогда будем искать решения системы
(6) в виде комбинаций 0. Тогда будем искать решения системы
(6) в виде комбинаций
которые имеют определенную частоту, то есть имеют вид (3). Для дальнейшего
важно отметить, что при малых  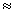 0 0  1 является почти чистым
электронным нейтрино, а при 1 является почти чистым
электронным нейтрино, а при  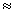  /2 - почти полностью
мюонным. Складывая первое из уравнений (6), помноженное на cos /2 - почти полностью
мюонным. Складывая первое из уравнений (6), помноженное на cos  , со вторым, помноженным на sin
, со вторым, помноженным на sin  , получаем условие того, что в
левой части также содержится только , получаем условие того, что в
левой части также содержится только  1: 1:
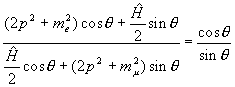
|
(8) |
Отсюда имеем определение угла  , который называется углом смешивания:
, который называется углом смешивания:
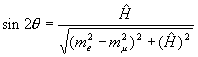
|
(9) |
Случай me > 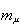 ,
то есть ,
то есть  =
= /4, соответствует
максимальному смешиванию и реализуется почти точно для системы нейтральных K-мезонов.
Состояния (7) имеют определенные массы, которые мы получаем из системы (6): /4, соответствует
максимальному смешиванию и реализуется почти точно для системы нейтральных K-мезонов.
Состояния (7) имеют определенные массы, которые мы получаем из системы (6):
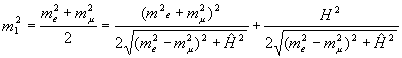
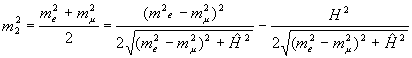 |
(10) |
Знаки в (10) соответствуют случаю 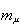 > me. Из (10) мы
видим, что при нулевом смешивании > me. Из (10) мы
видим, что при нулевом смешивании  = 0 получаем m1 = me, m2 =
= 0 получаем m1 = me, m2 =
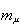 . В
присутствии смешивания происходит сдвиг масс. Если считать . В
присутствии смешивания происходит сдвиг масс. Если считать  очень малым, то очень малым, то
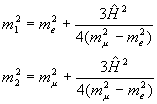
|
(11) |
Этим соотношением нельзя пользоваться при равенстве масс, в последнем случае
нужно применять точные формулы (10). Важно подчеркнуть, что именно состояния  1
и 1
и  2
имеют определенные массы и зависят от времени по закону 2
имеют определенные массы и зависят от времени по закону
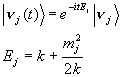 j=1,2.
j=1,2.
|
(12) |
Представим себе, что в начальный момент времени t = 0
родилось электронное нейтрино. Тогда из (7) и (12) получаем зависимость от
времени рассматриваемого состояния (общий множитель e-ikt мы опускаем)
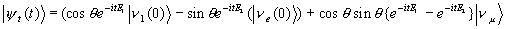
|
(13) |
Введем обозначение  m2 = m12 - m22
. Мы видим, что наряду с имевшимся вначале электронным нейтрино здесь появляется
и состояние нейтрино мюонного. Вероятность его появления по правилам квантовой
механики есть квадрат модуля амплитуды, то есть коэффициента при |νμ>.
Она, как видно из (13), зависит от времени и составляет m2 = m12 - m22
. Мы видим, что наряду с имевшимся вначале электронным нейтрино здесь появляется
и состояние нейтрино мюонного. Вероятность его появления по правилам квантовой
механики есть квадрат модуля амплитуды, то есть коэффициента при |νμ>.
Она, как видно из (13), зависит от времени и составляет
где мы измеряем расстояние L в метрах, энергию нейтрино - в
мегаэлектронвольтах и разность квадратов масс  m2-
в квадратных электронвольтах. Разумеется, мы учитываем малость масс нейтрино,
так что L = ct. Мюонная компонента имеет характерную осциллирующую зависимость;
это явление получило название осцилляций нейтрино. Что должно наблюдаться как
эффект осцилляций нейтрино? Мы знаем, что электронные нейтрино дают в результате
реакции с обменом W электрон, а мюонные - соответственно мюон. Следовательно,
пучок, первоначально состоящий из нейтрино электронных при прохождении его через
регистрирующую аппаратуру дает уже не только электроны, но и мюоны с
вероятностью, зависящей от расстояния до начальной точки, описываемой формулой
(14). Говоря попросту, надо искать рождение “чужих” лептонов. m2-
в квадратных электронвольтах. Разумеется, мы учитываем малость масс нейтрино,
так что L = ct. Мюонная компонента имеет характерную осциллирующую зависимость;
это явление получило название осцилляций нейтрино. Что должно наблюдаться как
эффект осцилляций нейтрино? Мы знаем, что электронные нейтрино дают в результате
реакции с обменом W электрон, а мюонные - соответственно мюон. Следовательно,
пучок, первоначально состоящий из нейтрино электронных при прохождении его через
регистрирующую аппаратуру дает уже не только электроны, но и мюоны с
вероятностью, зависящей от расстояния до начальной точки, описываемой формулой
(14). Говоря попросту, надо искать рождение “чужих” лептонов.
Эксперименты по поиску осцилляций нейтрино активно проводятся
и, как правило, приводят не к измерению эффекта, а к ограничениям на параметры в
(14)  и и  m2.
Ясно, что эффекта нет совсем, если хотя бы один из этих параметров равен нулю. В
последнее время появились сообщения о серьезных указаниях на существование
осцилляций нейтрино в экспериментах на японской установке “Супер-Камиоканде”. В
этих опытах изучался поток нейтрино от распадов частиц, рожденных в верхних
слоях атмосферы космическими лучами высоких энергий. В зависимости от углов
наклона к горизонту, под которыми приходят к прибору исследуемые нейтрино, они
проходят расстояния от нескольких десятков километров (прямо сверху) до многих
тысяч километров (прямо снизу). Результат непрерывных полуторагодовых измерений
оказался несовместимым с расчетами по теории без осцилляций. В то же время
введение осцилляций приводит к превосходному согласию с опытом. При этом
необходимы переходы νμ m2.
Ясно, что эффекта нет совсем, если хотя бы один из этих параметров равен нулю. В
последнее время появились сообщения о серьезных указаниях на существование
осцилляций нейтрино в экспериментах на японской установке “Супер-Камиоканде”. В
этих опытах изучался поток нейтрино от распадов частиц, рожденных в верхних
слоях атмосферы космическими лучами высоких энергий. В зависимости от углов
наклона к горизонту, под которыми приходят к прибору исследуемые нейтрино, они
проходят расстояния от нескольких десятков километров (прямо сверху) до многих
тысяч километров (прямо снизу). Результат непрерывных полуторагодовых измерений
оказался несовместимым с расчетами по теории без осцилляций. В то же время
введение осцилляций приводит к превосходному согласию с опытом. При этом
необходимы переходы νμ  e: e:
sin2 > 0.82, > 0.82,
5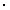 10-4
< 10-4
<  m2
< 6 m2
< 6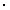 10-2 10-2
то есть требуются явно ненулевые их значения. Пока еще научное общественное
мнение не склонилось к окончательному признанию открытия осцилляций нейтрино и
ожидает подтверждения результата. Эксперименты продолжаются, а между тем
выяснилось, что еще более богатую информацию может дать исследование осцилляций
нейтрино c учетом их взаимодействия с веществом.
Осцилляции нейтрино в веществе
Выяснение возможностей, связанных с эффектами
распространения нейтрино в веществе, связано с работами Л. Волфенстайна
(L. Wolfenstein) и С.П. Михеева и А.Ю. Смирнова .
Рассмотрим опять случай двух нейтрино - электронного и
мюонного. В веществе имеются протоны и нейтроны в ядрах и электроны.
Взаимодействие обоих сортов нейтрино с протонами и нейтронами за счет обмена W и
Z происходит одинаково и потому не приводит к новым эффектам по сравнению с
распространением в вакууме. Совершенно по-иному обстоит дело с рассеянием
нейтрино на электронах. Нейтрино мюонное может взаимодействовать с электроном
только за счет обмена нейтральным бозоном Z, в то время как в рассеяние
электронного нейтрино (и антинейтрино) на электроне дает вклад и обмен
заряженным бозоном W. Действительно, например, W-
переходит в пару e, так что
процесс рассеяния идет по схеме e, так что
процесс рассеяния идет по схеме
 e+e e+e W- W-  e+e e+e
При рассеянии антинейтрино на электроне происходит слияние
их в W, а при рассеянии нейтрино происходит обмен W, при котором исходное
нейтрино дает электрон и W+, который поглощается исходным электроном,
давая конечное нейтрино. Для мюонного нейтрино такие переходы невозможны.
Итак, электронное нейтрино имеет дополнительное
взаимодействие с электроном, которое описывается дополнительным членом в первой
строчке (6):
VW| e(t)> e(t)>
Тогда система уравнений, описывающая зависимость волновой функции от времени,
изменяется:
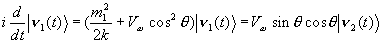
|
(15) |
В результате изменяются соотношения между электронной и мюонной компонентами
в смесях (7) и значения соответствующих масс, которые получаются из (15). Два
значения масс получаются такими:
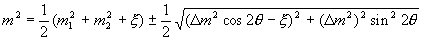
|
(16) |
где 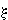 = 2kVW, причем эта величина связана с рассеянием электронного
нейтрино на электронах за счет обмена W. Электрослабая теория дает простое
выражение
= 2kVW, причем эта величина связана с рассеянием электронного
нейтрино на электронах за счет обмена W. Электрослабая теория дает простое
выражение
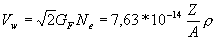 , ,
|
(17) |
где GF = (1.16637 + 0.00002).10-5
ГэВ-2 - известная константа Ферми, характеризующая слабые
взаимодействия, а Ne
- плотность электронов в веществе. Эта плотность пропорциональна атомному номеру
Z элемента и обычной плотности вещества p, что и отражено в численной форме
соотношения (17). Тогда величину 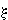 можно
представить в виде (A - атомный вес соответствующего элемента) можно
представить в виде (A - атомный вес соответствующего элемента)
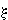 = 1.526.10-7Z = 1.526.10-7Z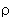 k/A эВ2, k/A эВ2,
|
(18) |
где плотность выражена в г/см3 и k - в МэВ.
Согласно системе (15), состояния с массами (16) являются
также смесями нейтрино двух сортов, но с другим углом смешивания  m.
Его связь с вакуумным углом следует из (15): m.
Его связь с вакуумным углом следует из (15):
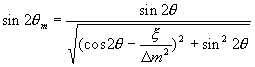
|
(19) |
Рассматривая выражение (16) для масс нейтринных состояний
и (19) для угла смешивания в веществе, мы получаем интереснейшее явление
резонансной осцилляции нейтрино в веществе. Пусть смешивание нейтрино в вакууме
очень мало, то есть sin 2 < 1. Представим себе, что нейтрино с некоторым импульсом k (первоначально
электронное) проходит через вещество с переменной плотностью, меняющейся
монотонно, например убывающей. Если при этом в каком-то слое плотность
< 1. Представим себе, что нейтрино с некоторым импульсом k (первоначально
электронное) проходит через вещество с переменной плотностью, меняющейся
монотонно, например убывающей. Если при этом в каком-то слое плотность 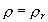 такова, что
выполняется равенство такова, что
выполняется равенство
то реализуется резонанс. Действительно, при 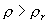 sin 2 sin 2 m << 1 и нейтрино остается
электронным. Однако при выполнении равенства (20) sin 2 m << 1 и нейтрино остается
электронным. Однако при выполнении равенства (20) sin 2 m
= 1, при дальнейшем уменьшении плотности sin 2 m
= 1, при дальнейшем уменьшении плотности sin 2 m
вновь становится малым, но это значит, что 2 m
вновь становится малым, но это значит, что 2 m
становится близким к m
становится близким к  ,
а ,
а  m- к m- к  /2.
Из (7) видно, что это соответствует уже почти полностью нейтрино мюонному. Таким
образом, при прохождении резонанса происходит смена сорта нейтрино, причем тем
полнее, чем меньше вакуумный угол смешивания. Поэтому такая резонансная
осцилляция является фактически единственной возможностью проявления малого
смешивания нейтрино. /2.
Из (7) видно, что это соответствует уже почти полностью нейтрино мюонному. Таким
образом, при прохождении резонанса происходит смена сорта нейтрино, причем тем
полнее, чем меньше вакуумный угол смешивания. Поэтому такая резонансная
осцилляция является фактически единственной возможностью проявления малого
смешивания нейтрино.
Явление резонансной осцилляции ярко проявляется также и в
зависимости масс нейтрино в веществе от плотности (16). Действительно, начнем с
выражения (16) со знаком минус, что в соответствии с уравнениями (15) описывает
начальное нейтрино электронное (поскольку содержит характерное для него
взаимодействие с электронами VW). Пусть плотность 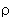 меняется проходя
через резонанс. Тогда квадрат массы до резонанса при малом угле меняется проходя
через резонанс. Тогда квадрат массы до резонанса при малом угле  равен me2
+ VW, а после резонанса -
равен me2
+ VW, а после резонанса -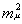 . При прохождении резонанса полностью
меняется сорт нейтрино. . При прохождении резонанса полностью
меняется сорт нейтрино.
Нужно отметить, что если вместо нейтрино рассмотреть
антинейтрино, то основное отличие заключается в знаке члена, описывающего
взаимодействие с обменом W. Знаки VW для нейтрино и антинейтрино
противоположны. Это означает, что условие резонанса достигается в зависимости от
знака  m2
или только для нейтрино, или только для антинейтрино. Например, если нейтрино
мюонное тяжелее электронного, то резонанс может наблюдаться только для
начального состояния электронного нейтрино, но не антинейтрино. m2
или только для нейтрино, или только для антинейтрино. Например, если нейтрино
мюонное тяжелее электронного, то резонанс может наблюдаться только для
начального состояния электронного нейтрино, но не антинейтрино.
Таким образом, распространение нейтринных (и антинейтринных)
пучков в веществе дает богатую физическую информацию. Если основные параметры,
то есть  m2 и m2 и  ,
известны, то, просвечивая нейтринным пучком некоторый объект, например планету,
звезду и т.д., по составу нейтринного пучка на выходе можно получить картину
распределения плотности внутри просвечиваемого объекта. Можно обратить внимание
на близкую аналогию с просвечиванием небольших объектов (в том числе и живых)
рентгеновскими лучами. ,
известны, то, просвечивая нейтринным пучком некоторый объект, например планету,
звезду и т.д., по составу нейтринного пучка на выходе можно получить картину
распределения плотности внутри просвечиваемого объекта. Можно обратить внимание
на близкую аналогию с просвечиванием небольших объектов (в том числе и живых)
рентгеновскими лучами.
Примеры возможных проявлений и применений
Явление нейтринных осцилляций пока не зарегистрировано на
опыте, однако есть указания на их существование, и они связаны как раз с
возможными резонансными явлениями. Дело в том, что методы регистрации
чувствительны в основном к электронным нейтрино (антинейтрино), поскольку
мюонные и тем более тау-нейтрино с энергиями в несколько мегаэлектронвольт не
могут дать реакции, например
37Cl +   37Ar
+ e-. 37Ar
+ e-.
которая используется в хлор-аргонном методе регистрации нейтрино. Это связано
с тем, что для рождения мюона нужно затратить энергию более 100 МэВ (и еще
больше для рождения тау). В то же время аналогичная реакция с электронным
нейтрино может происходить. Ядерные реакции в Солнце являются источником именно
электронных (анти-)нейтрино, так что использованный метод представлялся вполне
адекватным. Однако если по пути от точки рождения до прибора произошла
осцилляция и нейтрино превратилось, например, в мюонное, то реакция не
происходит, нейтрино становится “стерильным”. Это и могло бы послужить
объяснением дефицита солнечных нейтрино.
Сначала попытались использовать для объяснения обычные
(первый раздел) осцилляции в пространстве между Солнцем и Землей. Примесь
мюонных нейтрино определяется углом смешивания  . Обращаясь к
формуле (14) можно заключить, что доля таких стерильных нейтрино на Земле . Обращаясь к
формуле (14) можно заключить, что доля таких стерильных нейтрино на Земле
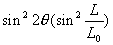
где угловыми скобками мы обозначили среднее значение. Усреднение необходимо,
так как расстояние L от Земли до Солнца в процессе измерения существенно
меняется из-за ее движения по орбите. Среднее значение функции sin 2x по
большому интервалу равно 1/2, следовательно, доля стерильных нейтрино составляет
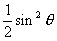
Таким образом, добиться подавления потока нейтрино от
Солнца вдвое, вообще говоря, можно, но для этого необходимо максимальное
смешивание sin 2 = 1. Поиски осцилляций показывают, что для широкого интервала масс нейтрино
такое большое смешивание исключается опытом. Кроме того, такое объяснение дает
одинаковое подавление нейтринного потока для всех энергий нейтрино, в то время
как экспериментальные результаты указывают на энергетическую зависимость
эффекта.
= 1. Поиски осцилляций показывают, что для широкого интервала масс нейтрино
такое большое смешивание исключается опытом. Кроме того, такое объяснение дает
одинаковое подавление нейтринного потока для всех энергий нейтрино, в то время
как экспериментальные результаты указывают на энергетическую зависимость
эффекта.
Более адекватным оказывается объяснение с помощью резонансных
осцилляций в веществе Солнца . Для того чтобы происходил резонансный переход
нейтрино в стерильное состояние, нужно, чтобы на некотором слое вещества Солнца
удовлетворилось условие (20). Пусть угол смешивания очень мал, так что cos 2 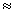 1.
Возьмем для примера значения параметров 1.
Возьмем для примера значения параметров
Z/A = 1.05, 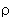 = 10 г/см2, E = 1 МэВ,
= 10 г/см2, E = 1 МэВ,
где первое число отражает тот факт, что Солнце состоит в основном из водорода
с примесью гелия и других элементов. Тогда условие (20) дает для разности
квадратов масс нейтрино
 m2
= 16.10-6 эВ2. m2
= 16.10-6 эВ2.
|
(21) |
Если одна из масс почти нуль, то вторая есть корень
квадратный из числа (21), то есть
m 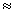 4.10-3
эВ. 4.10-3
эВ. |
(22) |
Именно такого порядка массы нейтрино необходимы, чтобы
использовать резонансный механизм нейтринных осцилляций в веществе для
объяснения дефицита солнечных нейтрино, включая и энергетическую зависимость
этого эффекта. Ситуация здесь такова: если существующие экспериментальные данные
получат окончательное подтверждение, то иного объяснения, кроме резонансной
осцилляции, предложить будет нельзя. Это будет важнейшим результатом,
открывающим путь к дальнейшему пониманию устройства физического мира. Кроме
того, мы получим новый способ рентгеновского просвечивания небесных тел, включая
и нашу Землю. Действительно, имея в виду, что плотности земных пород составляют
3-6 г/см3 в мантии и 9-12 г/см3 в ядре, мы убеждаемся, что
при массе нейтрино (22) условия резонанса достигаются для нейтрино с энергиями
порядка нескольких мегаэлектронвольт. Формируя такие пучки и проводя программу
просвечивания Земли с регистрацией эффекта на сети нейтринных станций можно
получать томограммы земной толщи. В перспективе это может привести как к
выяснению деталей строения Земли, так и к практическим результатам, например в
приложении к поискам глубоко залегающих полезных ископаемых.
Литература:
Б.А. Арбузов. Осцилляции нейтрино -
"рентген" для небесных тел?
|
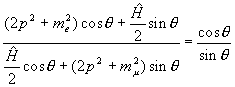
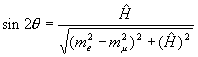
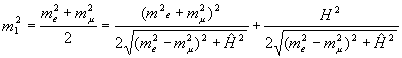
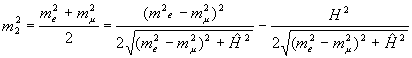
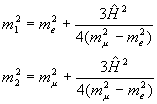
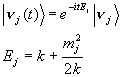 j=1,2.
j=1,2.