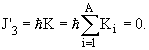6. Обобщенная модель ядра
Ограничимся рассмотрением
предельного варианта этой модели, в котором
предполагается:
- Сильная связь внешних, по отношению к
заполненным оболочкам, нуклонов с поверхностью
остова, в результате чего возникает устойчивая
равновесная деформация ядра. При этом будем
считать, что деформированное ядро имеет форму
эллипсоида вращения.
- Выполнение условия адиабатичности
(медленности) вращения деформированного ядра по
отношению к характерным скоростям внутреннего
движения:
 вращ<< вращ<<  внутр. внутр.
- Возможность приближенного описания движения
нуклонов во внутренней, вращающейся системе
координат в рамках одночастичной оболочечной
модели путем введения деформированной
потенциальной ямы.
В рассматриваемой модели
учитываются два типа ядерных движений:
коллективное вращение ядра относительно внешней
системы координат (x, y, z), обусловленное его
деформацией, и одночастичное движение нуклонов
относительно внутренней, вращающейся системы
координат (1, 2, 3) в деформированной
потенциальной яме.
Полный момент количества движения ядра  складывается из коллективного
вращательного момента ядра складывается из коллективного
вращательного момента ядра 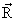 и
внутреннего момента нуклонов и
внутреннего момента нуклонов  ': ':
Моменты  'и 'и 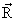 прецессируют вокруг направления
полного момента количества движения прецессируют вокруг направления
полного момента количества движения  . Так как аксиально-симметричное
эллипсоидальное ядро может вращаться только
вокруг оси перпендикулярной к оси симметрии 3, то
из этого вытекает (см. рис. 6.1), что вектор . Так как аксиально-симметричное
эллипсоидальное ядро может вращаться только
вокруг оси перпендикулярной к оси симметрии 3, то
из этого вытекает (см. рис. 6.1), что вектор 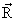 перпендикулярен оси 3 и проекции
полного и внутреннего угловых моментов на ось
симметрии должны быть равны между собой: перпендикулярен оси 3 и проекции
полного и внутреннего угловых моментов на ось
симметрии должны быть равны между собой:
J3 = J'3 =  K . K . |
(6.2) |
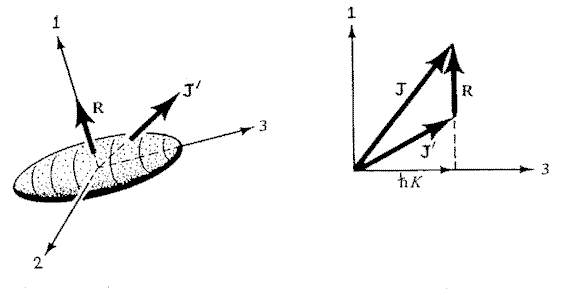
Рис. 6.1. Сложение моментов в
сфероидально деформированном ядре
|
Раньше мы говорили (см. раздел 4), что
момент количества движения в квантовой механике
характеризуют двумя квантовыми числами:
величиной J и проекцией M на некоторую
фиксированную ось квантования z. Более точно
фиксировать направление углового момента в
пространстве нельзя. Однако, если физическая
система обладает аксиальной симметрией, ее
угловой момент может иметь определенные
проекции (M, K) одновременно и на неподвижную
ось z и на вращающуюся ось симметрии 3. Появление
нового квантового числа K обусловлено
дополнительной ротоционной симметрией системы.
Итак, состояние движения
аксиально-симметричного ядра (| JMK>) можно характеризовать набором
квантовых чисел JMK>) можно характеризовать набором
квантовых чисел  , J, M, K,
где , J, M, K,
где  - квантовые числа,
определяющие, наряду с K, внутреннее состояние
нуклонной системы (это может быть, например,
перечень одночастичных уровней
деформированного потенциала, занимаемых
нуклонами в рассматриваемом состоянии).
Энергетические уровни ядра (2J + 1) раз
вырождены по квантовому числу M, так как энергия
ядра не зависит от ориентации спина - квантовые числа,
определяющие, наряду с K, внутреннее состояние
нуклонной системы (это может быть, например,
перечень одночастичных уровней
деформированного потенциала, занимаемых
нуклонами в рассматриваемом состоянии).
Энергетические уровни ядра (2J + 1) раз
вырождены по квантовому числу M, так как энергия
ядра не зависит от ориентации спина  относительно
внешней системы координат. Проекция относительно
внешней системы координат. Проекция  K полного углового момента K полного углового момента  на ось симметрии создается за
счет внутреннего движения нуклонов (см. (6.2)),
поэтому энергия ядра, вообще говоря, зависит от
квантового числа K. Однако, в таком ядре будут
вырождены состояния, отличающиеся только знаком
K, так как выбор положительного направления оси 3
физически не определен: аксиально-симметричное
эллипсоидальное ядро обладает плоскостью
симметрии перпендикулярной к оси 3. На самом деле,
из двух вырожденных (± K)-состояний нужно
построить одно истинное ядерное состояние,
являющиеся их линейной комбинацией, которое
остается инвариантным при отражениях в
плоскости симметрии и поворотах на на ось симметрии создается за
счет внутреннего движения нуклонов (см. (6.2)),
поэтому энергия ядра, вообще говоря, зависит от
квантового числа K. Однако, в таком ядре будут
вырождены состояния, отличающиеся только знаком
K, так как выбор положительного направления оси 3
физически не определен: аксиально-симметричное
эллипсоидальное ядро обладает плоскостью
симметрии перпендикулярной к оси 3. На самом деле,
из двух вырожденных (± K)-состояний нужно
построить одно истинное ядерное состояние,
являющиеся их линейной комбинацией, которое
остается инвариантным при отражениях в
плоскости симметрии и поворотах на  вокруг оси перпендикулярной к
оси 3. Поэтому мы будем считать, что волновая
функция ядра характеризуется K > 0. Ниже
мы покажем, что каждое внутреннее состояние с
определенным значением K > 0 может
стать основой для возникновения серии
вращательных уровней. вокруг оси перпендикулярной к
оси 3. Поэтому мы будем считать, что волновая
функция ядра характеризуется K > 0. Ниже
мы покажем, что каждое внутреннее состояние с
определенным значением K > 0 может
стать основой для возникновения серии
вращательных уровней.
Полную энергию деформированного ядра
можно представить в виде суммы энергии
коллективного вращения относительно внешней
системы координат и энергии движения нуклонов
относительно внутренней системы координат:
где
Eвращ = ( 2 - J23)/(2 2 - J23)/(2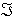 ) ) |
(6.4) |
- собственно вращательная энергия (этот член
зависит только от угловых, коллективных
переменных, характеризующих ориентацию ядра
относительно внешней системы координат);
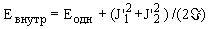 |
(6.5) |
- внутренняя энергия ядра (она зависит только от
переменных, характеризующих движение нуклонов
во внутренней системе координат);
Eвзаим = -2(J1J'1 + J2J'2)/(2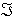 ) ) |
(6.6) |
- член, который описывает взаимодействие
внутренних и вращательных степеней свободы (так
называемое взаимодействие Кориолиса).
В квантовой механике величине (6.3) ставится в
соответствие оператор энергии, называемый также
гамильтонианом; при этом угловые моменты  и и  '
рассматриваются как операторы (см. определение
оператора проекции момента количества движения
в разделе 5). '
рассматриваются как операторы (см. определение
оператора проекции момента количества движения
в разделе 5).
Оператор Евзаим, вообще
говоря, смешивает различные внутренние
состояния ядра друг с другом. Действительно,
входящие в Евзаим операторы
проекций угловых моментов J1, J'1,...
меняют проекцию K угловых моментов  и и  ' на ось
симметрии 3 (см. 6.2) на величину ' на ось
симметрии 3 (см. 6.2) на величину  K = ± 1. Поэтому силы Кориолиса
могут смешивать внутренние нуклонные состояния,
у которых значения К отличаются на 1. Мера
энергетического воздействия сил (6.6) на
внутреннее движение нуклонов определятся
величиной
~ K = ± 1. Поэтому силы Кориолиса
могут смешивать внутренние нуклонные состояния,
у которых значения К отличаются на 1. Мера
энергетического воздействия сил (6.6) на
внутреннее движение нуклонов определятся
величиной
~  2/(2 2/(2 ) ~ ) ~  2ωвращ.
Характерная энергия перехода для смешиваемых
состояний равна |Eодн(К) - Еодн(К
± 1)|. Из этого следует, что взаимодействием
внутреннего и вращательного движения нуклонов
можно пренебречь тогда и только тогда, когда
выполняется условие адиабатичности 2ωвращ.
Характерная энергия перехода для смешиваемых
состояний равна |Eодн(К) - Еодн(К
± 1)|. Из этого следует, что взаимодействием
внутреннего и вращательного движения нуклонов
можно пренебречь тогда и только тогда, когда
выполняется условие адиабатичности  ωвращ<< ωвращ<<  ωвнутр = |Eодн(К)
- Еодн(К ± 1)|. Это условие, как
правило, выполняется для четно-четных ядер, но
нередко нарушается для деформированных ядер с
нечетным значением массового числа А, свойства
которых, как и сферических нечетных ядер,
определяются одночастичным состоянием
нечетного неспаренного нуклона (см. об этом ниже).
Как видно из рис. 6.5, в деформированном потенциале
энергетическое расстояние между уровнями с ωвнутр = |Eодн(К)
- Еодн(К ± 1)|. Это условие, как
правило, выполняется для четно-четных ядер, но
нередко нарушается для деформированных ядер с
нечетным значением массового числа А, свойства
которых, как и сферических нечетных ядер,
определяются одночастичным состоянием
нечетного неспаренного нуклона (см. об этом ниже).
Как видно из рис. 6.5, в деформированном потенциале
энергетическое расстояние между уровнями с  K = 1 может быть очень мало (~ K = 1 может быть очень мало (~ ωвращ), в
результате чего при описании нечетных ядер часто
возникает необходимость учета взаимодействия
вращательных и внутренних степеней свободы ядра.
Дальнейшее рассмотрение этой проблемы выходит
за рамки данного обзора, поэтому мы будем
предполагать, что условие адиабатичности
выполняется (см. допущение 2). ωвращ), в
результате чего при описании нечетных ядер часто
возникает необходимость учета взаимодействия
вращательных и внутренних степеней свободы ядра.
Дальнейшее рассмотрение этой проблемы выходит
за рамки данного обзора, поэтому мы будем
предполагать, что условие адиабатичности
выполняется (см. допущение 2).
В этом случае проквантованная энергия
деформированного сфероидального ядра может быть
найдена как среднее от оператора энергии (6.3) по
состоянию движения нуклонов | JMK>. Так как при адиабатическом
вращении внутреннее состояние ядра не меняется,
то при усреднении получим следующий результат: JMK>. Так как при адиабатическом
вращении внутреннее состояние ядра не меняется,
то при усреднении получим следующий результат:
E = { 2[J(J + 1) - K2]/(2A
) + 2[J(J + 1) - K2]/(2A
) + 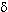 K,1/2A(J)}+ Eвнутр
, K,1/2A(J)}+ Eвнутр
, |
(6.7) |
где A(J) = (Eвзаим)ср. при К=1/2
- поправка к вращательной энергии, возникающая в
состояниях с К = 1/2 из-за действия сил Кориолиса, 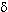 K,1/2 - символ Кронекера. K,1/2 - символ Кронекера.
Происхождение поправки A(J) легко
понять. Действительно, силы Кориолиса, как
отмечалось выше, меняют проекцию K угловых
моментов  и и  ' на
ось симметрии ядра на величину ' на
ось симметрии ядра на величину  K = ± 1. Поэтому при действии оператора Евзаим
на состояние
| K = ± 1. Поэтому при действии оператора Евзаим
на состояние
| JMK> будут рождаться
состояния | JMK> будут рождаться
состояния | JMK+1>
и | JMK+1>
и | JM|K-1|> (напомним,
что каждое истинное ядерное состояние
представляет суперпозицию ± К компонент,
вследствие чего характеризуется модулем
квантового числа К). Если ни одно из этих
состояний не идентично исходному состоянию, то
среднее от оператора Евзаим по
состоянию
| JM|K-1|> (напомним,
что каждое истинное ядерное состояние
представляет суперпозицию ± К компонент,
вследствие чего характеризуется модулем
квантового числа К). Если ни одно из этих
состояний не идентично исходному состоянию, то
среднее от оператора Евзаим по
состоянию
| JMK> будет равно 0. Это
имеет место при К > 3/2. При К = 1/2
состояние
| JMK> будет равно 0. Это
имеет место при К > 3/2. При К = 1/2
состояние
| JMK> = | JMK> = | JM|K-1|>, поэтому
A(J) = (Eвзаим)ср. при К=1/2 JM|K-1|>, поэтому
A(J) = (Eвзаим)ср. при К=1/2
 0. Поправка A(J)
должна быть линейной функцией J, так как оператор
Eвзаим зависит от проекций
углового момента 0. Поправка A(J)
должна быть линейной функцией J, так как оператор
Eвзаим зависит от проекций
углового момента  линейным
образом. Ее конкретное значение зависит от
структуры внутренней волновой функции состояния
| линейным
образом. Ее конкретное значение зависит от
структуры внутренней волновой функции состояния
| JMK=1/2>. JMK=1/2>.
Из формулы (6.7) видно, что каждое
внутреннее состояние, характеризуемое энергией
Евнутр и проекцией J'3 =  K внутреннего момента количества
движения на ось симметрии ядра, может стать
основой для возникновения серии вращательных
уровней, которые обычно называют вращательной
полосой. Если K > 0 угловые моменты
вращательных состояний могут принимать значения
J = K, K + 1, K + 2,... При K = 0 возможны только
четные значения угловых моментов вращательных
состояний: J = 0, 2, 4, 6,... (доказательство этого
результата полностью аналогично доказательству,
проведенному в разделе 5.2 для
аксиально-симметричного ротатора). На рисунках 6.2
и 6.3 показаны экспериментальные примеры
вращательных полос, базирующихся на разных
внутренних состояниях нечетного и четно-четного
ядер. K внутреннего момента количества
движения на ось симметрии ядра, может стать
основой для возникновения серии вращательных
уровней, которые обычно называют вращательной
полосой. Если K > 0 угловые моменты
вращательных состояний могут принимать значения
J = K, K + 1, K + 2,... При K = 0 возможны только
четные значения угловых моментов вращательных
состояний: J = 0, 2, 4, 6,... (доказательство этого
результата полностью аналогично доказательству,
проведенному в разделе 5.2 для
аксиально-симметричного ротатора). На рисунках 6.2
и 6.3 показаны экспериментальные примеры
вращательных полос, базирующихся на разных
внутренних состояниях нечетного и четно-четного
ядер.
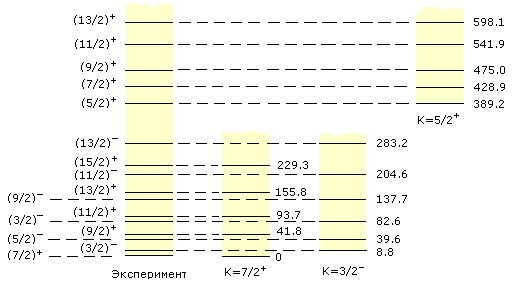
Рис. 6.2. Энергетические уровни ядра 249Bk.
Слева изображены все наблюдаемые уровни в
энергетическом интервале 0-600 КэВ.
Справа приведено разбиение этих уровней на три
вращательных полосы.
|

Рис. 6.3. Энергетические уровни ядра 168Er.
Под каждой вращательной полосой указаны
проекция K углового момента на ось симметрии и
четность π. Сверху над каждым
вращательным уровнем указаны спин J и энергия
возбуждения E соответствующего состояния.
Уровень энергии 821.19 кэВ отвечает квадрупольным
колебаниям деформированной ядерной поверхности. |
Займемся далее проблемой описания
внутреннего движения нуклонов во вращающейся
системе координат (1, 2, 3). В соответствии с
допущением 3) внутреннее движение можно
приближено свести к одночастичному движению
нуклонов в аксиально-симметричном
деформированном потенциале. В качестве такового
будем использовать деформированный потенциал
Нильссона (1955 г.):
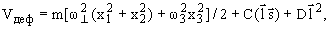 |
(6.8) |
где x1, x2 и x3 - координаты
нуклона во внутренней системе координат.
Первый член в выражении (6.8) является
потенциалом деформированного трехмерного
гармонического осциллятора (ср. с (4.4)), частоты
колебаний которого в направлении оси симметрии ( 3) и в направлении
перпендикулярном к ней ( 3) и в направлении
перпендикулярном к ней (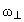 )
не совпадают между собой. К нему добавляется
обычный спин-орбитальный член и член, который
учитывает реальную радиальную зависимость
оболочечного потенциала, опуская вниз
одночастичные уровни энергии с большим
орбитальным моментом l (D < 0). )
не совпадают между собой. К нему добавляется
обычный спин-орбитальный член и член, который
учитывает реальную радиальную зависимость
оболочечного потенциала, опуская вниз
одночастичные уровни энергии с большим
орбитальным моментом l (D < 0).
Частота одночастичных колебаний в
первом приближении обратно пропорциональна
размеру ядра в том направлении, в котором
происходят колебания (см. упражнение 6.1). Пусть
деформированное ядро имеет полуось a = R0(1 + 2ε/3) вдоль оси симметрии
эллипсоида и полуось b = R0(1 -  /3) в направлении
перпендикулярном ей, где ε- параметр деформации (см. упражнение 3.5).
Тогда, пренебрегая членами порядка ε2, будем иметь /3) в направлении
перпендикулярном ей, где ε- параметр деформации (см. упражнение 3.5).
Тогда, пренебрегая членами порядка ε2, будем иметь
ω3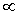 1/a = 1/[R0(1 + 2ε/3)]
1/a = 1/[R0(1 + 2ε/3)] 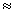 R0-1(1 - 2ε/3) и R0-1(1 - 2ε/3) и 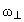 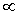 1/b = 1/[R0(1
- ε/3)] 1/b = 1/[R0(1
- ε/3)] 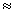 R0-1(1 +
ε/3).
Следовательно, мы можем определить частоты R0-1(1 +
ε/3).
Следовательно, мы можем определить частоты  3 и 3 и 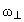 с помощью соотношений с помощью соотношений
где ω - частота колебаний
сферического гармонического осциллятора.
При малых значениях  выполняется соотношение выполняется соотношение  3 3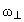 2 = 2 =  3,
что соответствует сохранению объема ядра.
Параметр 3,
что соответствует сохранению объема ядра.
Параметр  был определен
ранее (см. (4.5)). Параметры C и D подбираются так,
чтобы при был определен
ранее (см. (4.5)). Параметры C и D подбираются так,
чтобы при  = 0 наилучшим
образом воспроизводилась последовательность
уровней сферического оболочечного потенциала
(см. рис. (4.2)). Это дает следующие значения: = 0 наилучшим
образом воспроизводилась последовательность
уровней сферического оболочечного потенциала
(см. рис. (4.2)). Это дает следующие значения:
Рисунки 6.4 и 6.5 показывают как меняется
энергетический спектр одночастичных состояний в
потенциале Нильссона в зависимости от величины
параметра деформации  . При . При  = 0 картина уровней такая же как в
сферическом оболочечном потенциале.
Возникновение аксиально-симметричной
деформации снимает, с точностью до знака,
вырождение по квантовому числу m = 0 картина уровней такая же как в
сферическом оболочечном потенциале.
Возникновение аксиально-симметричной
деформации снимает, с точностью до знака,
вырождение по квантовому числу m 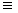 K. В результате каждая nlj орбита
расщепляется на (2j + 1)/2 двукратно вырожденных
энергетических уровня в соответствии со
значениями K = j, j - 1,...1/2 > 0. На
каждом таком уровне могут находиться не более
двух нуклонов одного сорта, отличающихся знаком
(± K) проекции углового момента на ось симметрии 3. K. В результате каждая nlj орбита
расщепляется на (2j + 1)/2 двукратно вырожденных
энергетических уровня в соответствии со
значениями K = j, j - 1,...1/2 > 0. На
каждом таком уровне могут находиться не более
двух нуклонов одного сорта, отличающихся знаком
(± K) проекции углового момента на ось симметрии 3.
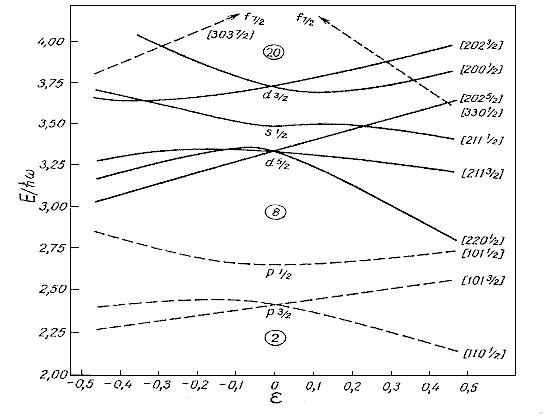
Рис. 6.4. Одночастичные уровни энергии в
сфероидальном потенциале Нильссона при
2 < N, Z < 20.
Уровни с положительной четностью изображены
сплошными, а с отрицательной - штриховыми
линиями. В квадратных скобках указаны
асимптотические квантовые числа N, n3, 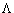 и K. и K. |
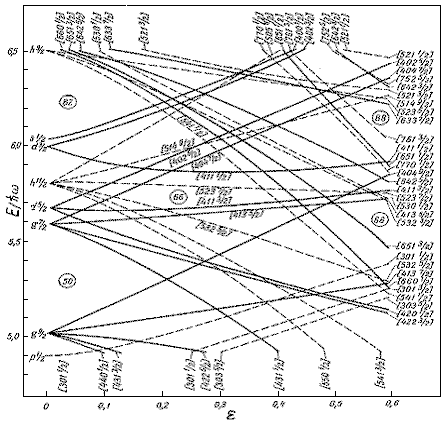
Рис. 6.5. Протонные одночастичные уровни
энергии в вытянутом сфероидальном потенциале
Нильссона при 50 < Z < 82. Обозначения
те же, что и на рис. 6.4.
|
При движении нуклона в сфероидально
деформированном потенциале строго сохраняются
только две физические величины - проекция K
углового момента нуклона на ось симметрии и
четность  . К ним можно
добавить приближенно сохраняющуюся величину N -
полное число квантов колебаний. В самом деле,
действие деформации на одночастичное движение
нуклона характеризуется энергией . К ним можно
добавить приближенно сохраняющуюся величину N -
полное число квантов колебаний. В самом деле,
действие деформации на одночастичное движение
нуклона характеризуется энергией  ( (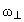 - -  3) = 3) =   . С другой стороны, из-за сохранения
четности, N может меняться самое малое на две
единицы . С другой стороны, из-за сохранения
четности, N может меняться самое малое на две
единицы
( = (-1)N в
трехмерном осцилляторе - см. раздел 4.2), что
предполагает переход между уровнями
осциллятора, разделенными энергией 2 = (-1)N в
трехмерном осцилляторе - см. раздел 4.2), что
предполагает переход между уровнями
осциллятора, разделенными энергией 2  >> >>    . Следовательно,
с хорошей точностью можно пренебречь
несохранением квантового числа N. . Следовательно,
с хорошей точностью можно пренебречь
несохранением квантового числа N.
При малых деформациях одночастичные
состояния можно характеризовать сферическими
квантовыми числами l и j. С возрастанием  состояния с
различными l и j (но с одинаковыми K и четностью)
начинают взаимодействовать друг с другом,
поэтому задача описания одночастичных состояний
сильно усложняется. Она снова упрощается, когда
деформация становится большой ( состояния с
различными l и j (но с одинаковыми K и четностью)
начинают взаимодействовать друг с другом,
поэтому задача описания одночастичных состояний
сильно усложняется. Она снова упрощается, когда
деформация становится большой ( > 0.3). В этом
случае одночастичные волновые функции в
потенциале (6.8) приблизительно совпадают с
одночастичными волновыми функциями
анизотропного осцилляторного потенциала (первый
член в (6.8)), так как при больших > 0.3). В этом
случае одночастичные волновые функции в
потенциале (6.8) приблизительно совпадают с
одночастичными волновыми функциями
анизотропного осцилляторного потенциала (первый
член в (6.8)), так как при больших  члены C члены C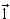 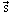 и D и D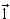 2 можно
трактовать как возмущения к деформированному
осцилляторному потенциалу и заменить на их
средние значения по соответствующему
одночастичному состоянию. 2 можно
трактовать как возмущения к деформированному
осцилляторному потенциалу и заменить на их
средние значения по соответствующему
одночастичному состоянию.
| В пределе больших деформаций
одночастичные состояния можно характеризовать
асимптотическими квантовыми числами: 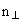 , n3, , n3, 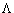 , , 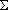 или N, n3,
или N, n3, 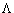 , K, , K,
где n3 - число квантов колебаний вдоль оси
симметрии; 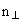 = n1 + n2
- число квантов колебаний в направлениях
перпендикулярных оси симметрии; N = n3 + = n1 + n2
- число квантов колебаний в направлениях
перпендикулярных оси симметрии; N = n3 + 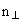 - полное число осцилляторных
квантов; - полное число осцилляторных
квантов; 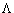 , , 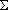 , K = , K = 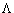 + +
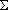 - проекции спинового,
орбитального и полного моментов количества
движения нуклона на ось симметрии ядра. - проекции спинового,
орбитального и полного моментов количества
движения нуклона на ось симметрии ядра. |
При усреднении спин-орбитального
взаимодействия получаем
Из этого выражения видно, что при больших
деформациях будут энергетически разделяться
одночастичные уровни с 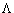 > 0, K = > 0, K = 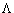 -
1/2 > 0, в которых проекции орбитального и
спинового моментов нуклона на ось симметрии
имеют разные знаки и уровни с -
1/2 > 0, в которых проекции орбитального и
спинового моментов нуклона на ось симметрии
имеют разные знаки и уровни с 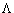 > 0, K = > 0, K = 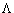 + 1/2 > 0, в которых эти проекции имеют
одинаковые знаки + 1/2 > 0, в которых эти проекции имеют
одинаковые знаки
На рисунках 6.4 и 6.5 асимптотические
квантовые числа N, n3, 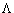 , K показаны в квадратных скобках.
Как видно из рисунков, для уровней с
фиксированным значением N при больших
положительных деформациях , K показаны в квадратных скобках.
Как видно из рисунков, для уровней с
фиксированным значением N при больших
положительных деформациях  (вытянутое ядро) четко прослеживается
тенденция уменьшения величины энергии уровня с
ростом числа продольных квантов n3, что
находится в согласии с тем фактом, что в
вытянутом ядре (вытянутое ядро) четко прослеживается
тенденция уменьшения величины энергии уровня с
ростом числа продольных квантов n3, что
находится в согласии с тем фактом, что в
вытянутом ядре   3 < 3 <  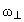 (см. (6.9)). Влияние
спин-орбитального взаимодействия при больших
деформациях иллюстрируют пары орбит [1 0 1 3/2], [1 0 1
1/2]; [2 1 1 3/2], [2 1 1 1/2]; [2 0 2 5/2], [2 0 2 3/2] на рис.
6.4, а также орбиты [4 1 3 7/2], [4 1 3 5/2]; [4 1 1 3/2],
[4 1 1 1/2]; [4 0 4 9/2], [4 0 4 7/2];... на рис. 6.5. (см. (6.9)). Влияние
спин-орбитального взаимодействия при больших
деформациях иллюстрируют пары орбит [1 0 1 3/2], [1 0 1
1/2]; [2 1 1 3/2], [2 1 1 1/2]; [2 0 2 5/2], [2 0 2 3/2] на рис.
6.4, а также орбиты [4 1 3 7/2], [4 1 3 5/2]; [4 1 1 3/2],
[4 1 1 1/2]; [4 0 4 9/2], [4 0 4 7/2];... на рис. 6.5.
Ранее отмечалось (см. раздел 4.3), что
одночастичная оболочечная модель не может быть
использована для описания основных и
низколежащих возбужденных состояний ядер,
имеющих устойчивую деформацию. Обобщенная
модель снимает это ограничение. Согласно этой
модели в основном состоянии сфероидального ядра
нуклоны заполняют все низшие уровни энергии
деформированного потенциала.
Если ядро четно-четное, то на каждой
заполненной нейтронной (протонной) орбите будут
находиться по два нейтрона (протона) с разными
знаками проекции углового момента на ось
симметрии. В результате основное состояние
четно-четного ядра будет иметь положительную
четность и нулевую проекцию внутреннего
углового момента на ось симметрии ядра:
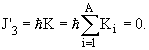
Из этого вытекает, что спин J этого состояния
также должен равняться нулю, так как оно служит
основой для вращательной полосы с K = 0 и J = 0, 2, 4, 6,...
Спин и четность основного состояния
ядра с нечетным A будут определяться значениями
квантовых чисел 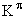 одночастичного
уровня, на котором находится последний непарный
нуклон. На основном состоянии нечетного ядра
базируется вращательная полоса с фиксированным K одночастичного
уровня, на котором находится последний непарный
нуклон. На основном состоянии нечетного ядра
базируется вращательная полоса с фиксированным K 0 и J = K, K+1, K+2... 0 и J = K, K+1, K+2...
Невращательные возбужденные
состояния деформированных ядер образуются при
переходе нуклонов с заполненных на
незаполненные орбиты, расположенные выше уровня
Ферми (последнего уровня, заполненного в
основном состоянии).
Приведем пример использования
обобщенной модели для описания спина и четности
основных состояний легких деформированных ядер.
Рассмотрим нечетные ядра, приведенные в первом
столбце таблицы 6.1. Согласно одночастичной
оболочечной модели со сферическим потенциалом
все они должны иметь в основном состоянии
спин-четность Jπ = (5/2)+,
так как заполняется орбита 1d5/2 (см. схему
уровней на рис. 4.2). Однако, это противоречит
экспериментальным данным, как видно из сравнения
столбцов 4 и 5 таблицы 6.1.
Таблица 6.1
Спин и
четность основных состояний легких
деформированных ядер |
Ядро |
Z |
N |
Jπ в основном состоянии |
| эксп. |
обол. мод. |
обобщ. мод. |
19 F |
9 |
10 |
(1/2)+ |
(5/2)+ |
(1/2)+ |
21 Ne |
10 |
11 |
(3/2)+ |
(5/2)+ |
(3/2)+ |
21 Na |
11 |
10 |
(3/2)+ |
(5/2)+ |
(3/2)+ |
23 Na |
11 |
12 |
(3/2)+ |
(5/2)+ |
(3/2)+ |
23 Mg |
12 |
11 |
(3/2)+ |
(5/2)+ |
(3/2)+ |
25 Mg |
12 |
13 |
(5/2)+ |
(5/2)+ |
(5/2)+ |
25 Al |
13 |
12 |
(5/2)+ |
(5/2)+ |
(5/2)+ |
Наблюдаемое несоответствие теории и
эксперимента объясняется тем, что при заполнении
оболочки 8 < N, Z < 20 возникает
вытянутая сфероидальная деформация ядерной
поверхности с ε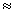 δ
δ 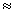 0.1 (см. рис. 5.4). В результате
спин J основного состояния ядра с нечетным A
определяется значением квантового числа K орбиты
деформированного потенциала, на которую
попадает непарный нуклон при данной деформации.
Ядро 19F имеет четное число нейтронов и
нечетное число протонов (см. столбцы 2 и 3 таблицы).
Нечетный непарный протон размещается на орбите
[2 2 0 1/2] c Kπ = (1/2)+ (см.
рис. 6.4), поэтому основное состояние этого ядра
согласно обобщенной модели имеет Jπ
= (1/2)+ (см.
последний столбец таблицы). В ядрах 21Ne, 21Na,
23Na и 23Mg непарная частица (нейтрон или
протон) попадает на орбиту [2 1 1 3/2],
поэтому эти ядра имеют в основном состоянии Jπ
= (3/2)+. Наконец,
ядра 25Mg и 25Al имеют по пять частиц
нечетной нуклонной компоненты в оболочке 8 < N, Z
< 20. Четыре из них заполняют орбиты
[2 2 0 1/2] и [2 1 1 3/2], а пятая, непарная
располагается на орбите [2 0 2 5/2],
вследствие чего спин-четность основных
состояний ядер 25Mg и 25Al равняется (5/2)+. 0.1 (см. рис. 5.4). В результате
спин J основного состояния ядра с нечетным A
определяется значением квантового числа K орбиты
деформированного потенциала, на которую
попадает непарный нуклон при данной деформации.
Ядро 19F имеет четное число нейтронов и
нечетное число протонов (см. столбцы 2 и 3 таблицы).
Нечетный непарный протон размещается на орбите
[2 2 0 1/2] c Kπ = (1/2)+ (см.
рис. 6.4), поэтому основное состояние этого ядра
согласно обобщенной модели имеет Jπ
= (1/2)+ (см.
последний столбец таблицы). В ядрах 21Ne, 21Na,
23Na и 23Mg непарная частица (нейтрон или
протон) попадает на орбиту [2 1 1 3/2],
поэтому эти ядра имеют в основном состоянии Jπ
= (3/2)+. Наконец,
ядра 25Mg и 25Al имеют по пять частиц
нечетной нуклонной компоненты в оболочке 8 < N, Z
< 20. Четыре из них заполняют орбиты
[2 2 0 1/2] и [2 1 1 3/2], а пятая, непарная
располагается на орбите [2 0 2 5/2],
вследствие чего спин-четность основных
состояний ядер 25Mg и 25Al равняется (5/2)+.
Мы рассмотрели простейший вариант
обобщенной модели, который отличается от
одночостичной оболочечной модели главным
образом введением статической деформации
среднего ядерного поля, приводящей к
возникновению вращательных степеней свободы
ядра. В более совершенных вариантах обобщенной
модели учитываются также коллективные степени
свободы, связанные с вибрациями ядерной
поверхности около равновесной деформированной
формы. Характерным примером таких вибраций может
служить уровень энергии 821.19 КэВ ядра 168Er
(см. рис. 6.3), на котором основывается вращательная
полоса Kπ = 2+. Подобные
состояния обнаружены почти у всех четно-четных
деформированных ядер. Все они интенсивно
распадаются в результате квадрупольных
электромагнитных переходов на уровни основной
вращательной полосы Kπ = 0+ и
интерпретируются как коллективные возбуждения
ядра, обусловленные поперечными квадрупольными
колебаниями ядерной поверхности относительно
аксиально-симметричной равновесной формы. Более
совершенные варианты обобщенной модели
рассматривают также взаимодействие между
разными вращательными полосами, вызываемое
силами Кориолиса, о важности учета которого для
нечетных ядер говорилось выше. Наконец, как и
оболочечная модель, обобщенная модель может быть
усовершенствована путем учета смешивания
различных нуклонных конфигураций остаточными
силами.
|