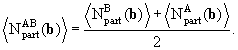9.2 Кинематические переменные

В эксперименте со встречными пучками ядер A и B полная энергия

а в эксперименте с фиксированной мишенью (E_B = m_B)

Для одинаковых ядер A = B энергия на пару нуклонов

где E_N − энергия нуклона в ядре пучка, A − число нуклонов.
    Ось z выбирается вдоль направления пучка частиц. Поперечный импульс и поперечная масса частицы определяются через компоненты трехмерного импульса:

где E, p_x, p_y, p_z и m − полная энергия, компоненты импульса и масса частицы.
    Быстрота частицы определяется как

(15)

Она очень просто меняется (сдвиг) при лоренцевском преобразовании вдоль оси z в новой системе отсчета, движущейся со скоростью β

Псевдобыстрота η может быть выражена через полярный угол частицы θ

(17)

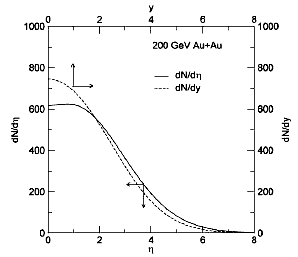
При больших (p >> m ) импульсах частицы y ≈ η.
    Примеры распределений по поперечному импульсу p_T, углу θ и псевдобыстроте η приведены на рисунках 38 и 39. Из рис. 38 видно, что 99 % числа частиц приходится на область малых
p_T < 2 ГэВ/с, которую называют областью мягких процессов. Рис. 39 демонстрирует, что 22 % частиц, приходящихся на широкую область полярного угла 45^o < θ < 135^o, соответствуют узкой области по псевдобыстроте |η| < 0.88 . Интервал |η| < 1 называют областью центральных быстрот и часто используют в представлении данных.

Рис. 38: Зависимость числа заряженных частиц от поперечного импульса pT при √s= 200 ГэВ в AuAu-столкновениях [125].

Рис. 39: Зависимость числа заряженных частиц от угла θ и псевдобыстроты η при √s= 200 ГэВ в центральных AuAu-столкновениях [125].

    Полезно понимать разницу в распределении частиц по быстроте и псевдобыстроте

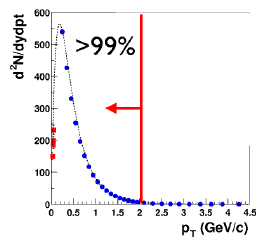
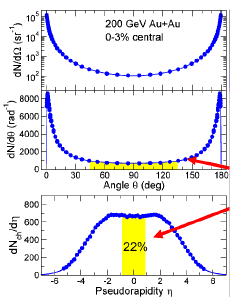
где β = th y − скорость частицы. В поперечной к направлению пучка плоскости скорость частиц меньше, поэтому в распределении dN/dηdp_T появляется плато при |η| < 1 , хотя вdN/dydp_T его нет. Это чисто кинематический эффект (см. рис. 40).

Рис. 40: Сравнение распределений по псевдобыстроте η и по быстроте у.

9.3 Число нуклонов двух ядер, участвующих в неупругом взаимодействии

В приближении абсолютно поглощающего ядра с резким краем вероятность взаимодействия пролетающего протона с ядром радиуса R_A

(19)

Здесь b − вектор прицельного параметра от центра ядра до пролетающего протона в поперечной плоскости, перпендикулярной импульсу протона.
    Для нуклона, взаимодействующего с ядерным веществом с сечением σ_in, и для ядра с размытым краем вероятность взаимодействия в модели Глаубера [126]

(20)

    Здесь в знаменателе стоит полное сечение неупругого взаимодействия протона с ядром

(21)

    Функция ядерной толщины, введенная в модели Глаубера [126],

зависит от плотности ядра, обычно задаваемой для тяжелых ядер в форме Ферми-плотности

(23)

    Перепишем формулу (20) в виде

(24)

и поясним физический смысл выражения (1 − exp(-σ_inAT(b)). Здесьexp(-σ_inAT(b) − вероятность протону пролететь с прицельным параметром b без взаимодействия, (1 − exp(-σ_inAT(b)) − вероятность пролететь, взаимодействуя с толщиной ядра AT(b).
    Полезно ввести вероятность ν неупругих взаимодействий нуклона при прохождении толщины ядра

(25)

Сумма по всем неупругим столкновениям приводит к выражению (24)

(26)

£    Зная вероятность ν взаимодействий (25), получим среднее число неупругих столкновений нуклона с ядром А ("число бинарных столкновений") при заданном прицел”ом параметре

(27)

    Для тяжелых ядер знаменатель (1 − exp(-σ_inAT(b)) в области b < R_A близок к единице и его для простоты часто опускают. Тогда

(28)

    Для двух сталкивающихся ядер A и B вводится функция перекрытия двух ядер

с которой вероятность неупругого ядро-ядерного взаимодействия

(30)

По аналогии с формулой (28) среднее число бинарных NN-столкновений в ядрах A и B определяется выражением

(31)

    Для столкновения двух ядер вводится еще одно понятие "числа участвующих (раненых)" нуклонов N_part [60]. Назовем условно ядро B налетающим. Его нуклоны с прицельным параметром s^B пролетают через ядро A с вероятностью взаимодействия (1 − exp(-σ_inAT_A(s^B)). Но не все из них будут "ранены" нуклонами ядра A . Их число пропорционально BT_А(s^B) . Поэтому среднее число участвующих нуклонов ядра B будет

(32)

Ясно, что это число меньше, чем число нуклонов = σ_inBT_B(b), испытавших неупругое столкновение в ядре B. Аналогично, число раненых нуклонов в ядре A

(33)

    Число пар раненых нуклонов при столкновении ядер A и B

(34)

    Напомним, что в выражениях (31-33) был опущен знаменатель по аналогии с (28), который неоходимо учесть при анализе A-зависимости интегральных по b чисел столкновений. В этом случае для равных ядер A = B

(35)

    Заметим, что фактор типа (1 − exp(-σ_inAT_A(b − s^B)) B формуле (32) учитывает возможность нуклону ядра B взаимодействовать во втором и последующих столкновениях с той же силой интенсивности с нуклонами ядра A7 что и в первом столкновении, но с меньшей вероятностью. Если же наблюдается процесс, в котором этот нуклон теряет свою способность рождать частицы (процесс с жестким взаимодействием), то можно таким фактором пренебречь. В этом случае число раненых нуклонов совпадает с числом бинарных столкновений ≈ и для двух ядер

≈

(36)

    Предполагается, что в общем случае следует учитывать оба типа столкновений [127]

(37)

причем их соотношение может меняться в зависимости от энергии. Доля x(s) учитывает вклад жестких процессов.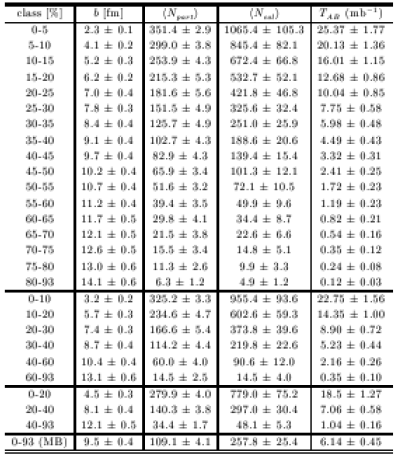
    В таблице 1 представлена зависимость от прицельного параметра числа раненых нуклонов , числа бинарных столкновений и функции ядерного перекрытия TAuAu. В процентах указана доля ∆σ/σ_geom полного неупругого сечения. Расчет выполнен при следующих значениях параметров: R(Au) = 6.38 Фм, d(Au) = 0.54 Фм и σ_in = 42 мб. С увеличением прицельного параметра растет доля полного сечения в заданном интервале ∆σ и уменьшаются значения чисел столкновения в области перекрытия двух ядер. Наибольшее отличие значений = 351 и = 1065 имеет место при самых центральных соударениях, а в периферической области при b ~ 2R_A они сравниваются. Эти зависимости используются для описания зависимости от центральности столкновения.

Рис. 41: Таблица 1. Значения и , полученные в модели Глаубера, для AuAu-столкновений при √s= 200 ГэВ.