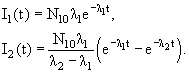Явление двойного β-распада было открыто в 1950 г. М. Инграм
и Дж. Рейнолдс обнаружили среди продуктов распада 130Te изотоп
130Xe, что объяснялось превращением изотопа 130Te
в изотоп 130Xe
cодновременным испусканием двух электронов и двух
антинейтрино. С тех пор исследование явления двойного β-распада
стало одним их эффективных методов изучения свойств нейтрино, проверки
Стандартной Модели.
В настоящее время известно ~3500 атомных ядер, представляющих собой различные
сочетания чисел протонов Z и нейтронов N. По существующим оценкам
число атомных ядер может составлять ~7000. Атомные ядра делятся на две большие
группы −
Из общего числа ~3500 известных атомных ядер стабильными являются ~350 ядер.
Изотопы − атомные ядра, имеющие одинаковое
число протонов (Z = const)
и разное число нейтронов.
Изотоны − атомные ядра, имеющие одинаковое число нейтронов (N = const) и разное число протонов.
Изобары − атомные ядра, имеющие одинаковое массовое число
A (A = Z + N) и разные числа нейтронов и протонов.
В таблице 1.2 для всех обнаруженных химических элементов приведены порядковый
номер, символ, название и минимальное и максимальное массовое число обнаруженных
изотопов. Химическим элементам с Z
= 113–118 названия пока не присвоены, они приводятся в специальных международных
обозначениях.
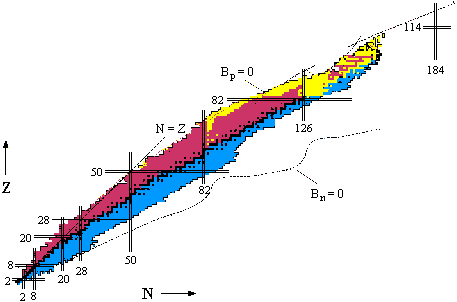
На рис. 1.1 показана N-Z диаграмма атомных ядер. Черными точками
показаны стабильные ядра. Область расположения стабильных ядер обычно называют
долиной стабильности. Для ядер долины стабильности характерно следующее
отношение числа нейтронов N к числу протонов Z:
N/Z = 0/98 + 0/015A2/3,
где
A = N + Z − массовое
число.
Легкие стабильные ядра (A < 40) имеют приблизительно равные числа
нейтронов и протонов. В области более тяжелых ядер отношение числа нейтронов к
числу протонов начинает возрастать и достигает величины 1.6 в районе A =
250. Это изменение легко
понять, если учесть короткодействующий характер ядерных сил и возрастающую
роль кулоновского взаимодействия протонов в ядре с ростом массового числа A.
Тяжелые ядра оказываются энергетически более устойчивыми, если содержат большее
число нейтронов N по сравнению с числом протонов Z. Наиболее
тяжелыми стабильными ядрами являются изотопы свинца 206, 207, 208Pb (Z
= 82) и висмута 209Bi (Z = 83). Стабильность
атомного ядра характеризуется его периодом полураспада. Целый ряд ядер долины
стабильности считаются стабильными. Однако они на самом деле могут распадаться с
очень большими периодами полураспада, часто превышающими время существования
Вселенной t = 13.7·109 лет. В качестве
примера можно привести изотопы 100Mo, 76Ge,
которые считаются стабильными изотопами, однако в настоящее время измерен их
период полураспада в результате двойного β-распада
T1/2(100Mo → 100Ru + 2e- + 2 ) = (7.6±0.4)·1018 лет,
) = (7.6±0.4)·1018 лет,
T1/2(76Ge →
76Se + 2e- + 2 ) = (1.5±0.1)·1021 лет,
) = (1.5±0.1)·1021 лет,
Аналогичная ситуация имеет место и в случае некоторых четно-четных тяжелых
ядер Z = 64–78, которые считаются
стабильными, однако имеют положительную энергию относительно α-распада. Их относят к
стабильным ядрам, например, изотопы 176–17972Hf. С левой
стороны от стабильных ядер находятся ядра, перегруженные протонами
(протоноизбыточные ядра), справа − ядра, перегруженные нейтронами
(нейтроноизбыточные ядра). Темным цветом на рис. 1.1 выделены атомные ядра,
обнаруженные в настоящее время. На основе различных моделей считается, что общее
число атомных ядер может составлять ~7000.
Связанное состояние атомного ядра определяется как состояние, стабильное
относительно испускания нейтронов или протонов. Линия Bp = 0 (Bp − энергия отделения протона)
ограничивает область существования атомных ядер слева (proton drip-line). Линия
Bn = 0 (Bn
− энергия отделения
нейтрона) − справа (neutron drip-line). Вне этих границ атомные ядра
существовать не могут, так как они распадаются за характерное ядерное время (~ 10-22 c) с испусканием
одного или нескольких нуклонов. Если среднее время жизни ядра τ < 10-22 c, обычно считается, что ядро
не существует, т.к. за это время не успевает образоваться структура характерная
для данного ядра. Обычно считается, что времена жизни радиоактивных ядер τ > 10-16 c. Времена жизни ядер,
обусловленные испусканием нуклонов, 10-23 c < τ < 10-16 c. Ядра, имеющие такие
времена жизни, обычно наблюдаются в виде резонансов в сечениях ядерных реакций.
Среднее время жизни ядра τ и ширина резонанса Г связаны соотношением
τ = ћ/ Г, τ[c] = 6.6·10-22/Г[МэВ].
Рассчитать границы испускания нуклонов довольно сложно, так как точность, с
которой известны энергии связи ядер (несколько сотен кэВ), недостаточна для
того, чтобы определить, будет ли ядро радиоактивным, или оно будет распадаться с
испусканием нуклона.
Поэтому точность предсказания границы существования атомных ядер составляет
4–5 единиц по A. В первую очередь это относится к границе, где
расположены атомные ядра нестабильные относительно испускания нейтрона.
В правом верхнем углу N–Z диаграммы расположена интенсивно исследуемая
в настоящее время область сверхтяжелых атомных ядер. Исследование сверхтяжелых
атомных ядер с Z = 109÷118 показало, что в этой области ядер
существенную роль в повышении их стабильности играют ядерные оболочки.
Достаточно хорошее согласие теоретических расчетов с полученными в последнее
время экспериментальными данными позволяет прогнозировать существование острова
стабильности в районе Z = 110÷116 и N = 178÷186. Ядра острова стабильности должны иметь
повышенную устойчивость по отношению к α- и β-распадам и спонтанному делению.
Теоретические оценки показывают, что времена жизни ядер, расположенных в центре
острова стабильности могут составлять ~105 лет. Сложность
проникновения на остров стабильности связана с тем, что трудно подобрать
комбинации соответствующих ядер, использование которых в качестве мишени и
налетающей частицы позволило бы попасть в центр острова стабильности.
Свойства свободных нейтрона и протона
| Характеристика |
n |
p |
| Масса, МэВ/c2 |
939.56536±0.00008 |
938.27203±0.00008 |
| Квантовое число − спин |
1/2 |
ћ[1/2(1/2 + 1)]1/21/2 |
| Спин, ћ = 6.58×10–22МэВ·c |
ћ[1/2(1/2 + 1)]1/2 |
|
Электрический заряд,
qe= (1.602176487 ± 40)×10-19Кл |
(–0.4 ± 1.1)×10-21qe |
|qp+qe|/qe< 10-21 |
Магнитный момент,
μ = eћ/2mpc = 3.15×10-18 МэВ/Гс |
–1.9130427±0.000005 |
+2.792847351±000000028 |
| Электрический дипольный момент d, e·см |
< 0.29×10–25 |
< 0.54×10–23 |
| Барионный заряд В |
+1 |
+1 |
| Зарядовый радиус, Фм |
|
0.875±0.007 |
Радиус распределения
магнитного момента, Фм |
0.89±0.07 |
0.86±0.06 |
| Изоспин I |
1/2 |
1/2 |
| Проекция изоспина Iz |
–1/2 |
+1/2 |
| Кварковый состав |
udd |
uud |
| Квантовые числа s ,c, b, t |
0 |
0 |
| Среднее время жизни |
(885.7±0.8)с |
> 2.1×1029 лет |
| Четность |
+ |
+ |
| Статистика |
Ферми-Дирака |
| Схема распада |
n → p + e- +
 e e |
|
|
Энергия связи ядра
Есв(A, Z) = [Zmp + (A - Z)mn - M(A,
Z)]c2
Формула Вайцзеккера
Eсв = a1A - a2A2/3
- a3Z2/A1/3 - a4(A/2 - Z)2/A
+ a5A-3/4.
где a1 = 15.75 МэВ; a2 = 17.8 МэВ; a3 = 0.71 МэВ; a4 = 23.6 МэВ;

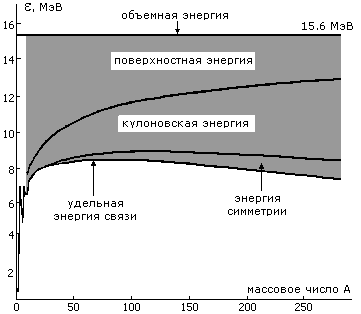
Вклад различных членов в удельную энергию
связи ядра ε = Eсв/A.
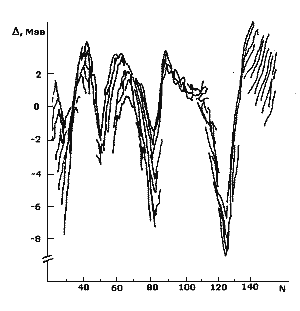
Разность Δ между
предсказаниями формулы Вайцзеккера и экспериментальными значениями энергии
связи ядер с различными числами нейтронов N. Наиболее
сильные расхождения с экспериментальными значениями наблюдаются в
окрестностях магических чисел
нейтронов N= 20, 28, 50, 82, 126
|
Радиоактивность
Радиоактивностью называется способность атомного ядра самопроизвольно
распадаться с испусканием частиц.
Радиоактивный распад ядра возможен в том случае, когда он энергетически
выгоден, т.е. сопровождается выделением энергии. Условием этого является
превышение массы M исходного ядра суммы масс mi
продуктов распада,
M > ∑mi.
Это условие является необходимым, но не всегда достаточным. Радиоактивный
распад может быть запрещен другими законами сохранения – сохранения момента
количества движения, электрического заряда, барионного заряда и другими.
Радиоактивный распад характеризуется временем
жизни радиоактивного изотопа, типом испускаемых частиц, их энергиями.
Основными видами радиоактивного
распада являются:
К более редким видам радиоактивного распада относятся:
- двойной β-распад − испускание атомным
ядром двух электронов и двух антинейтрино, испускание атомным ядром двух
позитронов и двух нейтрино, захват атомным ядром электрона с испусканием
позитрона и двух нейтрино,
- кластерная радиоактивность − испускание атомным ядром лёгких ядер
от 12C до 32S,
- протонная радиоактивность − испускание протонов из основного
состояния ядра,
- двухпротонная радиоактивность − испускание двух протонов из
основного состояния ядра,
- нейтронная радиоактивность − испускание нейтронов из основного
состояния ядра.
Во всех типах радиоактивного распада (кроме γ-распада)
изменяется состав ядра – число протонов Z, массовое число
A или и то и другое одновременно.
На характеристики радиоактивного распада существенное влияние оказывает
взаимодействие, вызывающее распад. α‑распад
вызывается сильным взаимодействием. β-распад вызывается слабым
взаимодействием, а гамма-распад − электромагнитным.
Существуют различные причины, в силу которых времена жизни нестабильных ядер
могут изменяться на несколько порядков.
- Малая интенсивность взаимодействия, за счет которого происходит распад.
- Испускание
тяжелых положительно заряженных частиц сильно подавляется потенциальным
барьером.
- Время жизни
радиоактивного ядра сильно зависит от энергии, выделяющейся при распаде. Если
эта энергия мала, то время жизни резко возрастает. Сильной зависимостью от
энергии распада Q характеризуются α-распад и слабое взаимодействие.
- Время жизни
радиоактивного ядра сильно зависит от разности значений спинов исходного и
конечного ядер.
Для характеристики скорости (вероятности) радиоактивного распада используются
три взаимосвязанные величины - постоянная распада λ,
среднее время жизни τ и период полураспада T1/2.
Закон радиоактивного распада
Постоянная распада λ − вероятность
распада ядра в единицу времени. Если в образце в момент времени t
имеется N радиоактивных ядер, то количество ядер
dN, распавшихся за время dt, пропорционально
Nλ и интервалу времени dt:
dN = −λNdt.
Знак «–» означает, что в результате распада количество
радиоактивных ядер в образце уменьшается.
Закон радиоактивного распада
имеет вид:
N(t) = N0e−λt,
где
N0 – количество радиоактивных ядер
в образце в исходный момент времени t = 0, N(t) –
количество радиоактивных ядер, не распавшихся в образце к моменту времени
t.
Среднее время жизни τ:
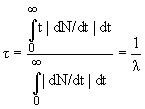 .
.
Период полураспада T1/2 –
время, в течение которого первоначальное количество радиоактивных ядер
уменьшается в два раза:
T1/2 = ln2/λ=0.693/λ
= τln2.
Активность источника
Активность источника I − среднее количество распадов ядер
источника в единицу времени.
| I(t) = −dN/dt = λN(t) = λN0e−λt
= I0e−λt. |
(1.1) |
За единицу активности принимают число распадов, происходящих за 1 с в 1 г
радия, находящегося в равновесии с продуктами распада. Эта единица активности
называется «Кюри» и равна 3.7·1010 распадов в секунду. В системе СИ
используется единица активности «Беккерель», которая равна 1 распаду в секунду.
1 Кюри = 3.7·1010 распадов в секунду.
1 Беккерель = 1 распад в секунду.
1 Кюри = 3.7·1010 Беккерель.
Измеряя активность источника I(t) можно определить постоянную
распада λ. Для
изотопов с малыми постоянными распада и, соответственно, большими периодами
полураспада используется соотношение (1.1). В этом случае количество ядер N
во время измерения практически не изменяется и может быть определено методами
масс-спектрометрии. Для изотопов с большими постоянными распада используется
соотношение
I(t) = I0e−λt.
Если построить зависимость активности источника I(t) от времени t в полулогарифмическом
масштабе ln I(t), то угол наклона φ прямой к оси t будет
определять величину λ.
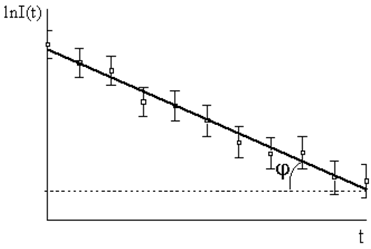
Рис. 1.2. График распада радиоактивного препарата в полулогарифмическом
масштабе. Сплошная линия соответствует закону радиоактивного распада I(t) = I0e−λt.
Сказанное выше относится к одному изотопу с одним каналом распада.
Зависимость активности от времени может быть представлена суммой двух или
нескольких экспонент, т. е.
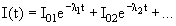 |
(1.2) |
Последнее показывает, что в источнике присутствует несколько радиоактивных
изотопов с различными периодами полураспада. При этом распад каждого из
радиоактивных элементов происходит независимо.
В случае, если радиоактивный препарат содержит два различных радиоактивных
изотопа, не связанных между собой цепочкой последовательных распадов
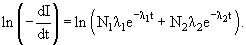
Если периоды полураспада изотопов сильно различаются λ1 >> λ2, а первоначальное число радиоактивных
ядер каждого изотопа сравнимо, то при малых t выполняется соотношение
ln(−dI/dt) ≈ ln(N1λ1).
При больших t
ln(−dI/dt) ≈ ln(N2λ2).
На рис. 1.3 в полулогарифмическом масштабе показано изменение во времени
активности источника, состоящего из двух компонентов с различными постоянными
распада λ1 и λ2.
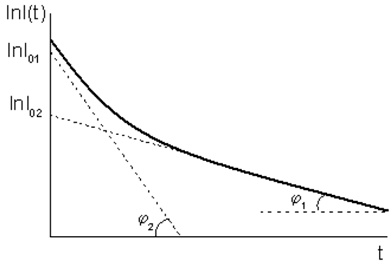
Рис.1.3. Изменение во времени усредненной активности источника, состоящего из
двух изотопов, не связанных между собой цепочкой последовательных распадов.
Тангенсы углов φ1 и
φ2 наклона этих
прямых равны, соответственно, постоянным распада λ1 и λ2, т.е.
tgφ1 = λ1, tgφ2 = λ2.
Соотношение (1.2) справедливо только в том случае, если радиоактивные изотопы
не связаны между собой генетически. Часто ядро II, возникающее в результате
радиоактивного распада ядра I, также радиоактивно и имеет другую постоянную
распада λ2. В ряде случаев такое последовательное
превращение радиоактивных ядер приводит к образованию большого числа различных
радиоактивных изотопов (рис. 1.4). В этом случае зависимость активности
источника от времени будет более сложная.
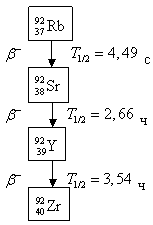
Рис. 1.4. Цепочка последовательных β--распадов ядер-изобар A = 92.
Для двух последовательных распадов N1(t) → N2(t) →
N3(t) изменение числа ядер N1(t) и числа ядер N2(t) описывается
системой уравнений
dI1/dt = −λ1N1(t),
dI2/dt = −λ2N2(t) + λ1N1(t). |
(1.3) |
Число ядер N1(t) уменьшается за счет их распада. Число
ядер N2(t) уменьшается
за счет их распада и увеличивается за счет распада ядер N1.
В случае начальных условий t = 0, N1(0) =
N10, N2(0) = 0 решение системы уравнений (1.3) имеет вид
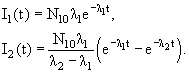
Если
λ1 > λ2, кривая
распада будет иметь ту же форму, как и в случае независимого распада двух
изотопов с различными периодами полураспада. Если λ1 < λ2, кривая логарифма активности будет иметь
максимум (рис. 1.5). Подъём на начальном участке обусловлен накоплением ядер N2. При больших временах
(λ1t >> 1) вклад от
экспоненты с λ1 становится
пренебрежимо малым и наступает радиоактивное равновесие, при котором активности
сравниваются, а соотношение
между числами N1 и N2 становится независимым от времени.
N1/N2 = λ2/λ1.
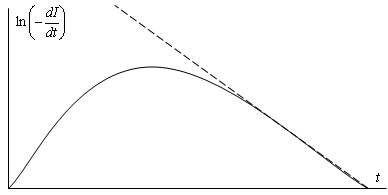
Рис. 1.5. Зависимость логарифма активности от t для цепочки распадов N1(t) → N2(t) → N3(t) при
λ1
< λ2.
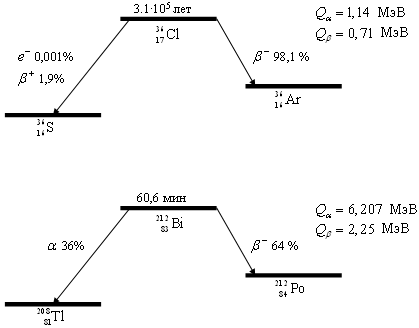
Распады изотопов 36Cl и 212Bi, имеющих несколько каналов
распада.
Изотоп
36Cl распадается
по трем различным каналам.
- β--распад с вероятностью 98.1%
- β+-распад с вероятностью 1.9%
- е-захват с вероятностью 0.001%
Изотоп 212Bi распадается
по двум различным каналам.
- β--распад с вероятностью 64%
- α-распад с вероятностью 36%
Вековое равновесие
В случае нескольких последовательных распадов
N1(t) → N2(t) → N3(t) → ...,
когда период полураспада ядер N1 намного превосходит периоды полураспада
остальных ядер
T1/2(N1) >> T1/2(N2),
T1/2(N3),...
число ядер различных изотопов связаны между собой соотношением
N1(t) : N2(t) : N3(t) : ... =
T1/2(N1) : T1/2(N2) : T1/2(N3)
: ...
Это состояние называется вековым равновесием.
Часто радиоактивный изотоп может иметь несколько различных каналов распада,
например, как это имеет место в случае распада изотопа 36Cl. Изотоп
36Cl c вероятностью 98.1% распадается в результате β--распада, с
вероятностью 1.9% в результате β+-распада, е-захват составляет 0.001%.
В этом случае полная вероятность распада λ складывается из вероятностей распада по
различным каналам
λ = λ1 + λ2 + λ3.
Относительная вероятность распада ωi по каналу
i определяется соотношением ωi = λi/λ.
Если за время измерения число ядер изотопа изменяется мало, то активность
источника I и парциальные интенсивности распадов по
отдельным каналам I1,
I2, I3 связаны соотношением
I = λN = I1 + I2 + I3 = λ1N
+ λ2N + λ3N,
при этом выполняется соотношение
I1 : I2 : I3 = λ1
: λ2 : λ3.
В случае, если интенсивность изотопа со временем уменьшается, интенсивность
распада по отдельным каналам Ii будет описываться соотношением
Ii(t) = λiN(t) = λiN(0)e−λt,
т.е. изменение интенсивности распада по каналу i Ii(t) будет определяться величиной λ. Величина
Ti = ln2/λi называется парциальным
периодом полураспада.
Активация изотопа
Активацией называется процесс получения радиоактивного вещества при облучении
стабильных ядер нейтронами, протонами и другими видами излучения. Количество
активированных ядер зависит от количества атомов в мишени, времени облучения и
эффективного сечения ядерной реакции, в которой образуется исследуемый изотоп.
Эффективное сечение σ некоторого процесса характеризует вероятность
рассматриваемого взаимодействия частицы с ядром и определяется как отношение
числа событий данного типа в единицу времени, приходящееся на одно ядро мишени,
к потоку налетающих частиц через единицу поверхности мишени. Если слой вещества,
содержащий nс ядер,
пересекают ν частиц/см2с, то число актов взаимодействия
m, вызванных ими в единицу времени, будет равно
m = vnсσ.
Эффективное сечение измеряется в барнах: 1 б = 10-24 см2.
Пусть на образец, содержащий n ядер, падает поток ν
частиц/см2с, а эффективное сечение захвата падающих частиц с
образованием радиоактивного ядра равно σ. Тогда в образце в секунду
образуется νnσ радиоактивных ядер. Необходимо
учесть, что часть вновь образовавшихся ядер в процессе активации распадается. За
время dt образуется νnσdt ядер,
а распадается λNdt, где N − количество
накопленных к моменту времени t активируемых ядер. В результате изменение количества радиоактивных
ядер описывается соотношением
dN = νnσdt − λNdt, или
dN/dt = νnσ − λN.
При больших временах активации t > 1/λ рост числа
радиоактивных ядер практически прекращается (dN/dt → 0). Это происходит, когда число
образующихся радиоактивных ядер окажется практически равным числу
распадающихся, т.е. когда число радиоактивных ядер N(t) → Nн = νnσ/λ.
Величина
Nн называется активацией насыщения.
Зависимость активации N(t)
от времени облучения t имеет вид
N(t) = Nн(1 − e−λt).
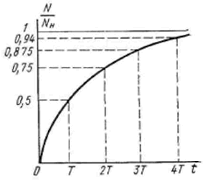
Рис. 1.6. Зависимость
активации образца от времени.
Зависимость активации образца от времени показана на рис. 1.6. Практически
насыщение достигается за время облучения, соответствующее
4–5 периодам полураспада. При t << T распадом можно пренебречь. В этом случае N(t) = νnσt, т. е. в начале облучения
число радиоактивных ядер растёт линейно со временем.
Для получения радиоактивных изотопов часто используют нейтроны, так как для
них не существует электростатических сил отталкивания от ядра. В 1935 г. Ферми
обнаружил, что наведенная радиоактивность во много раз увеличивается, если
источник нейтронов и облучаемую мишень окружить водородосодержащим веществом,
например парафином.
Как оказалось, это связано с тем, что нейтроны при соударениях с равными им
по массе протонами быстро теряют энергию и распространяются в среде с тепловыми
скоростями. Вероятность захвата тепловых нейтронов атомными ядрами обратно
пропорциональна их скорости и достигает максимальной величины. Кроме того,
тепловые нейтроны, испытывая в парафине большое число соударений, движутся
хаотично и могут пересекать облучаемую мишень несколько раз.
При захвате теплового нейтрона ядром с массовым числом A образуется
«компаунд» − ядро A+1 в возбужденном состоянии.
Избыток энергии, равный энергии связи нейтрона в ядре A+1 (5–8 МэВ), может выделиться в
виде γ-квантов. Такие реакции носят название радиационного захвата
нейтрона. Они могут быть представлены в общем виде как
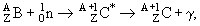
где В − исходное ядро, C* и C − ядро-продукт соответственно в
возбужденном и основном состояниях.
Пучки радиоактивных ядер
Используется два основных метода получения пучков радиоактивных ядер. Эти два
метода взаимно дополняют друг друга и могут быть использованы в зависимости от
конкретной физической задачи.
Сравнение методов ISOL и IN-FLIGHT показано на рис. 1.7.
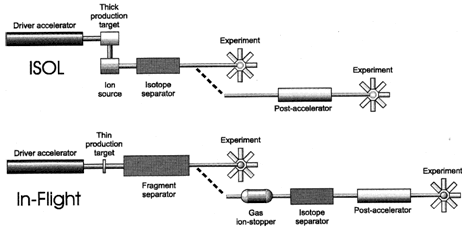
Рис. 1.7. Сравнение методов получения и сепарации вторичных пучков
ISOL и IN-FLIGHT.
Пучки радиоактивных нейтроноизбыточных ядер, образующихся в реакции деления,
могут быть получены также с помощью интенсивных источников нейтронов − ядерных
реакторов − или ускоренных дейтронов.
Метод ISOL (Isotop Separation On
Line).
Этот метод основан на образовании ионов тепловых скоростей в твердой, жидкой
или газовой среде; извлечении, разделении, ионизации и последующем ускорении их
до энергий требуемых для эксперимента.
В результате бомбардировки ускоренным пучком толстой мишени (Thick
Production Target) в ней образуются радиоактивные ядра в широком
диапазоне Z и A, которые остаются в веществе мишени. Образовавшиеся ядра
затем извлекают из мишени. После извлечения из мишени ионы разделяются с помощью
масс-сепаратора (Isotope Separator) и могут быть использованы в прецизионных
экспериментах с низкими энергиями (10–500 кэВ) или ускорены во втором ускорителе. Таким образом, в
методе ISOL используются две ускорительные системы. Одна для получения
первичного пучка (Driver Accelerator) и создания вторичных частиц
в толстой мишени, вторая (Post Accelerator) − для ускорения
вторичных частиц. Второй ускоритель обеспечивает необходимую для физических
исследований энергию пучка радиоактивных ядер.
В методе ISOL генерируются пучки вторичных частиц высокой интенсивности с
энергией до 25 МэВ/нуклон. Время извлечения радиоактивных ядер из мишени, в
которой они образуются, и время их транспортировки к ускорителю вторичных
пучков, определяет диапазон времен жизни экзотических ядер, которые могут быть
исследованы этим методом.
Метод In-Flight (метод фрагментации ускоренных ионов на мишени)
Метод In-Flight оптимален для получения вторичных пучков короткоживущих
изотопов со временем жизни от 100 нс.
В этом методе пучки радиоактивных ядер получаются в периферических
столкновениях тяжелой заряженной частицы с легким ядром мишени и последующей
сепарацией выделенных по Z и A продуктов фрагментации. Первичный
пучок имеет энергию от 50 МэВ/нуклон до 1 ГэВ/нуклон. Радиоактивные
осколки-фрагменты, образующиеся в результате столкновений, летят преимущественно
вперед по направлению падающей частицы со скоростями ~0.9-1.0 от
скорости падающей частицы. Для получения радиоактивных пучков в этом методе
используются тонкие мишени. Для короткоживущих изотопов интенсивность вторичных
пучков в методе In-Flight может превосходить интенсивность пучков,
полученных методом ISOL.
Для разделения изотопов и выделения определенных изотопов используются
электромагнитные сепараторы (Fragment Separator). Пучки частиц на
выходе сепаратора могут либо непосредственно использоваться в эксперименте, либо
после замедления в газовой среде (Gas Ion-Stopper) разделяться на
отдельные пучки по Au Z и снова ускоряться (Post-accelerator)
для проведения экспериментов с ускоренными радиоактивными пучками.
Методы регистрации радиоактивных ядер
Прогресс в исследовании радиоактивности в
значительной мере связан с развитием методов получения и регистрации
радиоактивных ядер и излучений. Явление радиоактивности было открыто в
результате воздействия излучения на фотографическую пластинку. Регистрация
вспышек света, возникавших при попадании
α-частиц в
экран, покрытый сернистым цинком, лежала в основе детектора, с помощью которого
Г. Гейгер и Э. Мардсен исследовали рассеяние α-частиц атомами золота.
Информативность любого эксперимента определяется возможностями тех
детекторов, которые в нём используются. История ядерной физики и физики частиц
это, по существу, история создания всё новых методов регистрации частиц и
совершенствования старых. Создание новых методов детектирования частиц
неоднократно отмечалось Нобелевскими премиями.
Детекторы служат как для
регистрации частиц, так и для определения их энергии, импульса, траектории
движения частицы и других характеристик. Для регистрации частиц часто используют
детекторы, которые максимально чувствительны к регистрации определенной частицы
и не чувствуют большой фон создаваемый другими частицами.
Часто в экспериментах
приходится выделять «нужные» события на гигантском фоне «посторонних» событий,
которых может быть в миллиарды раз больше. Для этого используют различные
комбинации счётчиков и методов регистрации, применяют схемы совпадений или
антисовпадений между событиями, зарегистрированными различными детекторами,
отбор событий по амплитуде и форме сигналов и т. д.
Часто используется селекция частиц по времени пролёта ими определённого
расстояния между детекторами, магнитный анализ и другие методы, которые
позволяют надёжно выделить различные частицы.
Один из принципов регистрации
частицы состоит в следующем. Заряженная частица, двигаясь в нейтральной среде
детектора (газ, жидкость, твердое тело, аморфное или кристаллическое), вызывает
в результате электромагнитных взаимодействий ионизацию и возбуждение атомов
среды. Таким образом, вдоль пути движения частицы появляются свободные заряды
(электроны и ионы) и возбужденные атомы. Если среда находится в электрическом
поле, то в ней возникает электрический ток, который фиксируется в виде короткого
электрического импульса. Детекторы, использующие этот принцип, называют
ионизационными.
При возвращении возбужденных
атомов в основное состояние излучаются фотоны, которые могут быть
зарегистрированы в виде оптической вспышки в видимой или ультрафиолетовой
области. Этот принцип используется в сцинтилляционных детекторах.
При определенных условиях
траекторию пролетающей заряженной частицы можно сделать видимой. Этот способ
реализуется в так называемых трековых детекторах.
Гамма-кванты также
регистрируются по вторичным заряженным частицам – электронам и позитронам,
возникающим в среде вследствие фотоэффекта, комптон-эффекта и рождения
электрон-позитронных пар.
Нейтрино, возникшее в
результате реакции, в силу исключительно малого сечения взаимодействия со средой
(≈ 10-20 барн)
в большинстве случаев вообще не регистрируется детектором. Тем не менее, факт
его появления может быть установлен. Дело в том, что ускользнувшее от
непосредственного наблюдения нейтрино уносит с собой определённую энергию,
импульс, спин, лептонный заряд. Недостачу обнаруживают, регистрируя все
остальные частицы и используя законы сохранения энергии, импульса, момента
количества движения, электрического заряда, лептонного заряда и др. Такой анализ
позволяет не только убедиться, в том, что нейтрино действительно образовалось,
но и установить его энергию и направление вылета из точки реакции.
Быстрораспадающиеся атомные
ядра детектор «не успевает» зафиксировать. В этом случае они регистрируются по
продуктам распада.
Общие требования к детектирующей аппаратуре сводятся к определению типа
частицы (идентификации) и её кинематических характеристик (энергии, импульса и
др.). Часто тип частицы известен заранее и задача её наблюдения упрощается. Во
многих экспериментах, используются сложные комплексы, состоящие из большого
числа детекторов различного типа. Такие комплексы, фиксируя практически все
частицы, возникающие в результате взаимодействия, дают достаточно полное
представление об изучаемом явлении.
Основными характеристиками
детектора являются:
- эффективность −вероятность регистрации частицы при
попадании её в детектор;
- временнóе разрешение − минимальное время, в течение
которого детектор фиксирует две частицы как отдельные;
- мёртвое время или время восстановления − время, в
течение которого детектор после регистрации частицы либо вообще теряет
способность к регистрации следующей частицы, либо существенно ухудшает свои
характеристики;
- энергетическое разрешение − точность определения
энергии частицы;
- пространственное разрешение − точность определения
координаты частицы.
Радиоактивный распад – статистический процесс
Каждое радиоактивное ядро может распасться в
любой момент. Закономерности распада атомного ядра наблюдаются только в среднем,
в случае распада достаточно большого количества радиоактивных ядер.
Если радиоактивный источник содержит N радиоактивных ядер и их число практически
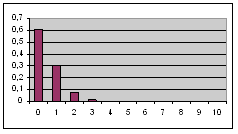
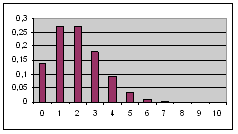
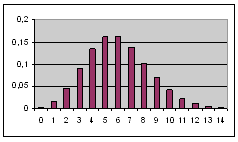
не изменяется за время измерения, то вероятность ω(n) того, что за время t распадется
n радиоактивных ядер,
описывается распределением Пуассона
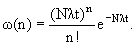
Величина
Nλt характеризует
среднее число частиц, распадающихся за время t, и представляет собой
среднее число отсчетов
 , которое получается в случае
многократного проведения измерений с одинаковым временем измерения t
, которое получается в случае
многократного проведения измерений с одинаковым временем измерения t
 = Nλt.
= Nλt.
Используя величину
 , распределение Пуассона можно переписать
в виде
, распределение Пуассона можно переписать
в виде
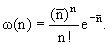



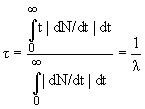 .
.