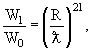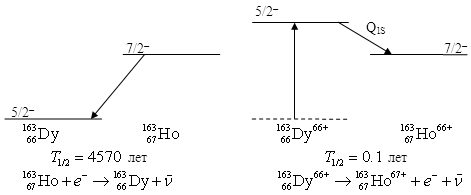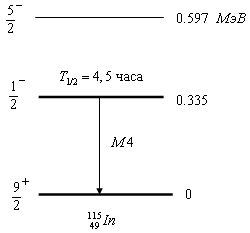Радиоактивность атомных ядер

Радиоактивность
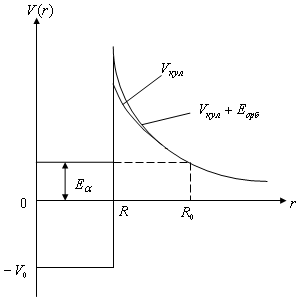
Альфа-распад
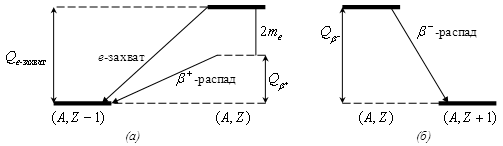
Бета-распад
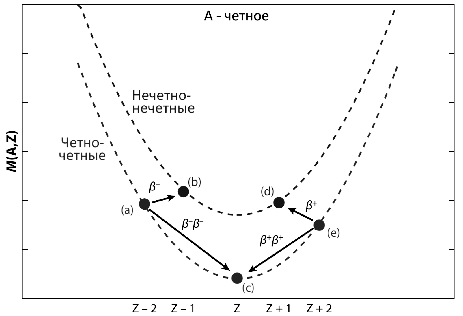
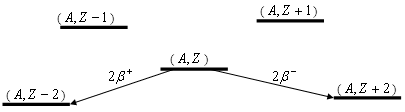
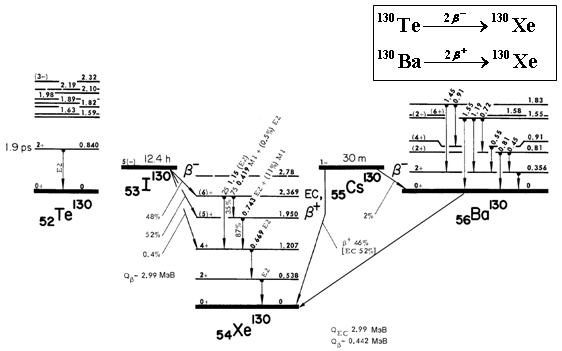
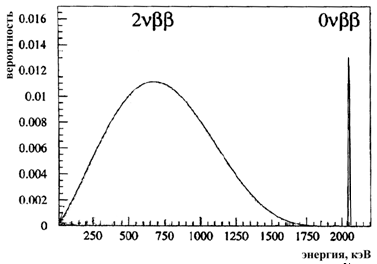
Двойной β-распад
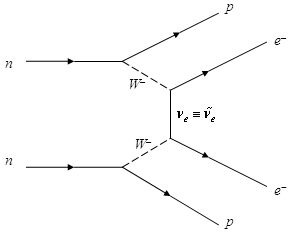
Безнейтринный двойной β-распад
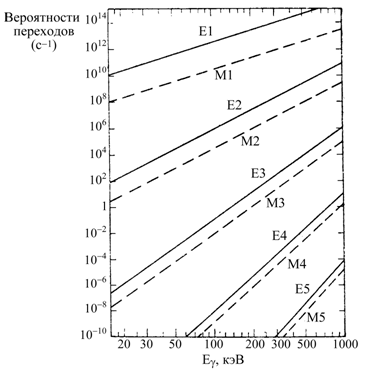
Гамма-переходы в ядрах
Ядерная изомерия
Внутренняя конверсия γ-квантов
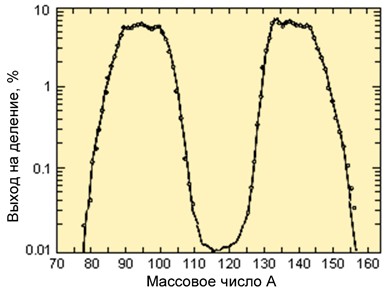
Деление атомных ядер
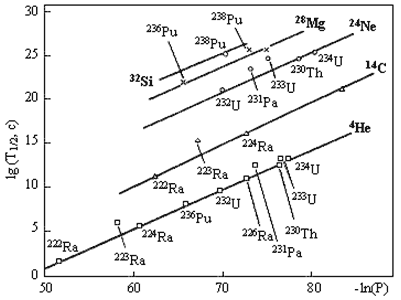
Кластерная радиоактивность
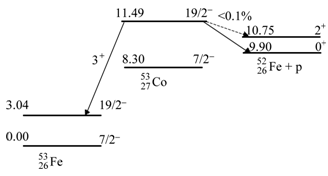
Протонная радиоактивность
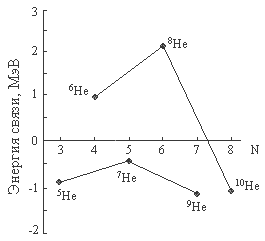
Нейтронная радиоактивность
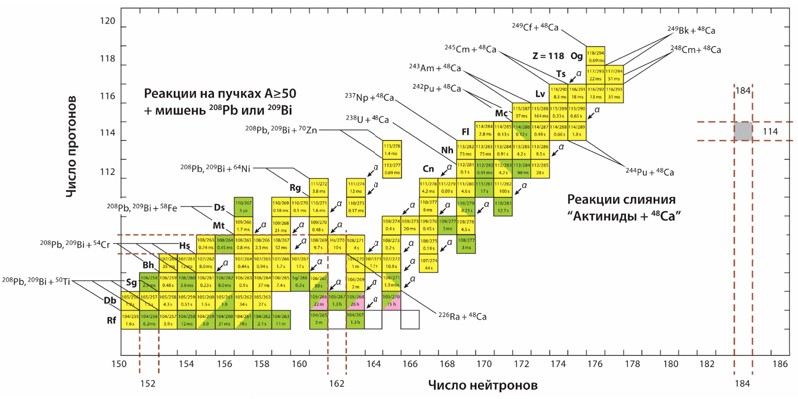
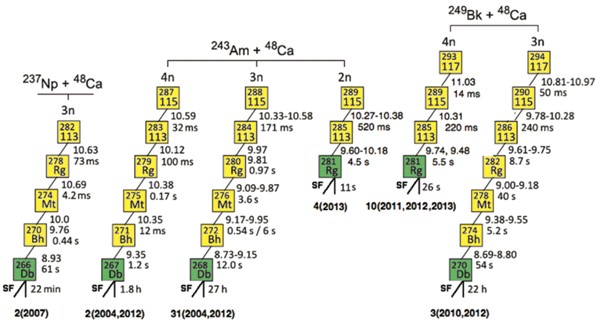
Сверхтяжелые элементы
Радиоактивные изотопы. Научные проблемы. Практические приложения

    Атомное ядро является связанной системой, состоящей из Z протонов и N нейтронов, A = (N + Z) − массовое число.
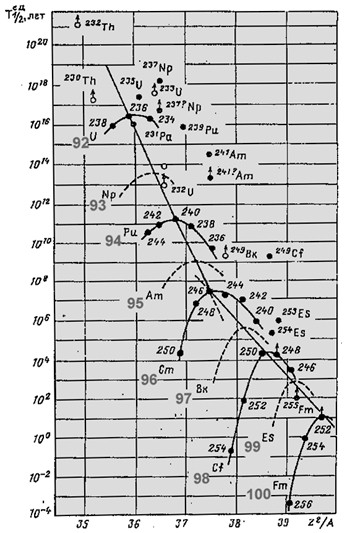
    В настоящее время известно ~3500 атомных ядер. В зависимости от соотношения между числом нейтронов N и числом протонов Z в ядре атомные ядра делятся на две группы: стабильные ядра и радиоактивные ядра. Число стабильных ядер ~300. На рис. 1 показана N-Z-диаграмма атомных ядер. Стабильные атомные ядра показаны черным цветом.

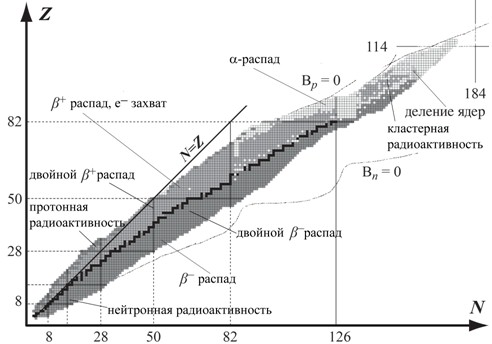
Рис. 1. N-Z-диаграмма атомных ядер. Типы радиоактивного распада ядер.

    Для стабильных ядер связь между числом нейтронов N и числом протонов Z дается соотношением

В области легких стабильных ядер число протонов примерно равно числу нейтронов. В тяжелых стабильных ядрах число нейтронов в 1.5–2.0 раза превышает число протонов.
    Важной характеристикой атомных ядер является энергия связи ядра W(A,Z) − минимальная энергия, необходимая для того, чтобы разделить атомное ядро на протоны и нейтроны

m_p − масса свободного протона (m_pc² = 938.27 МэВ), m_n − масса свободного нейтрона
(m_nc² = 939.56 МэВ), M(A,Z) − масса атомного ядра, состоящего из Z протонов и A = N + Z нуклонов.
    В капельной модели энергия связи ядра описывается формулой Бете-Вайцзеккера

a₁A − объемная энергия ядра, характеризует свойство насыщения ядерных сил, при котором каждый нуклон эффективно взаимодействует лишь с ближайшими соседями,
a₂A^2/3 − поверхностная энергия ядра, описывает уменьшение энергии связи нуклонов, находящихся на поверхности ядра,
a₃Z(Z−1)/A^1/3 − кулоновская энергия отталкивания протонов,
a₄(A − 2Z)²/A − энергия симметрии ядра, описывает свойство протонов и нейтронов, являющихся фермионами и подчиняющихся принципу Паули,
a₅A^-3/4 − энергия симметрии ядра, описывает дополнительную энергию связи между двумя тождественными нуклонами, находящимися на одном энергетическом уровне.
    Коэффициенты a₁ − a₅ подбираются так, чтобы наилучшим образом описать экспериментальные значения энергии связи ядер, расположенных в районе долины стабильности.

a₁ = 15.6 МэВ, a₂ = 17.2 МэВ, a₃ = 0.72 МэВ, a₄ = 23.6 МэВ,

    Удельная энергия связи ядра

    Относительные вклады отдельных членов удельной энергии связи ядра в полную удельную энергию связи ядра показаны на рис. 2.

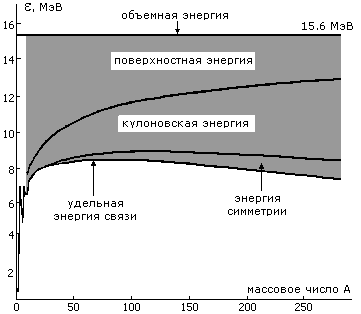
Рис. 2. Вклад различных членов в удельную энергию связи ядра

 
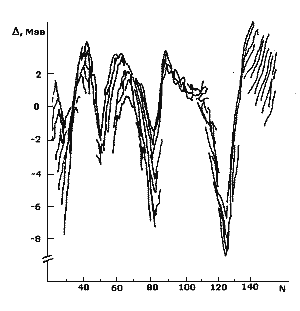
Рис. 3. Разность Δ между предсказаниями формулы Бете-Вайцзеккера и экспериментальными значениями энергии связи ядер с различными числами нейтронов N. Наиболее сильные расхождения с экспериментальными значениями наблюдаются в окрестностях магических чисел
нейтронов N = 20, 28, 50, 82, 126.

    На рис. 3 показана разность между экспериментальными значениями энергии связи ядра и расчетами на основе соотношения (3). Наблюдающиеся расхождения в районе чисел нейтронов
N = 20, 28, 50, 82, 126 являются указанием на оболочечную структуру атомных ядер.
    Зная энергию связи атомного ядра легко рассчитать границы существования атомных ядер, различные типы радиоактивного распада атомных ядер, энергии распадов, спектры и другие энергетические характеристики ядер.
    Граница существования атомных ядер в области легких изотопов соответствует условию B_p < 0, где B_p − энергия отделения протона, т.е. существование атомного ядра становится энергетически невыгодным, если

B_p = W(A,Z) − W(A−1,Z−1) < 0.

    Граница существования атомных ядер в области тяжелых изотопов химических элементов соответствует отрицательной энергии отделения нейтрона

B_p = W(A,Z) − W(A−1,Z) < 0.

Радиоактивность

    Анри Беккерель, исследуя связь между явлением испускания рентгеновских лучей и люминесценцией, обнаружил, что соли урана испускают какое-то излучение, которое проникает сквозь черную бумагу, в которую он обычно заворачивал фотопластинки и вызывает их почернение. 2 марта 1896 г. А. Беккерель на заседании Парижской академии наук сообщил, что открытое им явление отличается от флюоресценции, возникающей в кристаллах соли урана под действием солнечного света.
    А. Беккерель: «Я особенно настаиваю на следующем факте, кажущемся мне весьма многозначительным… Те же кристаллы, содержащиеся в темноте, в условиях когда возникновение радиации под действием солнечного света исключается, дают, тем не менее, фотографические отпечатки. В среду 26-го и в четверг 27 февраля 1896 г. солнце появлялось лишь с большими перерывами. Я отложил совсем подготовленные опыты и, не трогая кристаллов соли урана, установил кассеты в ящике стола в темноте. В следующие дни солнце не появлялось вовсе, но, проявив пластинки 1 марта, я обнаружил на них совершенно отчетливые контуры».
    А. Беккерель обнаружил, что излучение солей урана, подобно рентгеновскому излучению, способно ионизовать воздух. Наблюдение ионизации окружающей среды стало одним из первых методов регистрации радиоактивности.
    В 1898 г. Э. Резерфорд показал, что излучение, обнаруженное А. Беккерелем, имеет две различные компоненты.

• Сильно поглощаемая тонкими металлическими фольгами компонента излучения, названная α-излучением. Позднее им было установлено, что α-излучение представляет собой ионизованные атомы ⁴He.
• Более слабое поглощаемое излучение представляло собой электроны, открытые Дж. Томсоном в 1897 г.

    В 1900 г. П. Виллардом была открыта третья компонента радиоактивного излучения − нейтральное излучение − γ-излучение.

    Изучая ионизующую способность различных минералов, супруги Пьер и Мария Кюри обнаружили радиоактивность тория, полония и радия (1898 г.). К концу 1904 г., благодаря работам Э. Резерфорда и Ф. Содди, было обнаружено около 40 элементов, обладающих радиоактивными свойствами.
    Так было открыто новое неизвестное ранее физическое явление − радиоактивность − способность некоторых химических элементов самопроизвольно распадаться, превращаясь в другие химические элементы. После открытия атомного ядра Э. Резерфордом в 1911 г. стало ясно, что явление радиоактивности связано с различными распадами, происходящими в атомном ядре.
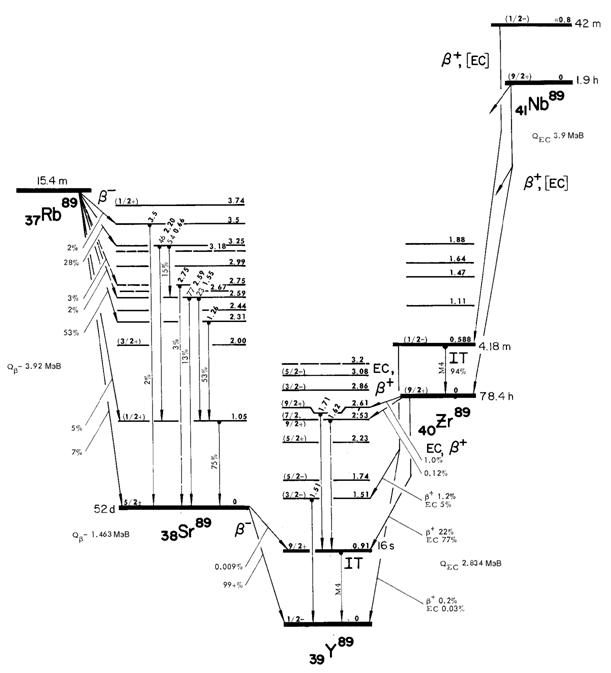
    В таблице 1 и на рис. 1 приведены различные типы радиоактивного распада атомных ядер. Ниже на нескольких примерах обсуждаются основные характеристики различных типов радиоактивного распада.

Таблица 1

Типы радиоактивного распада ядер

Тип радиоактивности ядер	Тип испускаемых частиц	Год открытия	Авторы открытия
Радиоактивность атомных ядер	Излучение, вызвавшее потемнение фотопластинок	1896	A. Becquerel
α-распад	4Не	1898	E. Rutherford
β−-распад	e−	1898	E. Rutherford
β+-распад	e+ν	1934	I. et F. Joliot-Curie
е-захват	ν	1938	L. Alvarez
Гамма-распад	γ-квант	1900	P. Villard
Ядерная изомерия	γ, е-захват, β+, β−, деление	1921	O. Hahn
Спонтанное деление	Два осколка сравнимой массы	1940	Г.Н. Флеров, К.А. Петржак
Двойной β-распад	e−e−2e	1950	M.G. Ingram, J.H. Reynolds
Протонная радиоактивность	р	1981	S. Hofmann
Кластерная радиоактивность	14С	1984	H. Rose, G. Jones, Д.В. Александров
β−-распад ионизованного атома	e−	1992	H. Jung et al.
Двухпротонная радиоактивность	2р	2002	J. Giovinazzo, B. Blank et al. M.Pfutzner, E.Badura et al.

Альфа-распад

    Явление α-распада состоит в том, что тяжелые ядра A > 60  самопроизвольно распадаются с испусканием α-частицы − ядра ⁴He.

    Энергетическое условие α-распада

Энергия α-частицы E_α

(7)

    Периоды полураспада α-радиоактивных ядер изменяются в широких пределах:
T_1/2(²¹⁹Po) = 5.3·10^-8 с, T_1/2(¹⁸²W) > 8.3·10¹⁸ лет, в то время как α-частицы имеют энергии 4–10 МэВ. α-распад происходит в результате сильного взаимодействия. Большое различие в периодах α-распада объясняется необходимостью α-частицы пройти через потенциальный барьер V_барьер для того чтобы выйти из ядра.

(8)

 Рис. 4. Потенциал, в котором находится α-частица.

    На рис. 5 показан α-распад изотопа ²⁵³Es .

Рис. 5. Альфа-распад изотопа  ²⁵³Es.

    При α-распаде конечное ядро может оказаться не только в основном но и в одном из возбужденных состояний. Распады на возбужденные состояния приводят к тонкой структуре энергетического спектра вылетающих α-частиц.
    Экспоненциальная зависимость вероятности α-распада от энергии α-частицы приводит к тому, что распады на возбужденные состояния конечного ядра происходят с очень низкой интенсивностью, потому что при возбуждении конечного ядра уменьшается энергия α-частицы.
    Экспериментально удается наблюдать распады на вращательные уровни, имеющие относительно низкие энергии возбуждения. Допустимые значения орбитального момента l, который может унести α‑частица, ограничены законами сохранения момента количества движения и чётности.:

|J_f  – J_i| ≤ l ≤ J_f  + J_i ,

где J_f и J_i – спины конечного и начального ядер. Из закона сохранения чётности следует, что значение l должно быть чётным, если чётности начального и конечного ядер совпадают, и нечётным, если эти чётности различны.

Бета-распад

    Существуют три типа β-распада

β−-распад (A,Z) → (A,Z+1) + e− + e,

(9)

β+-распад (A,Z) → (A,Z−1) + e− + νe,

(10)

    Бета-распад происходит в результате слабого взаимодействия. Он наблюдается в широком диапазоне масс атомных ядер от нейтрона до самых тяжелых ядер. Бета-распад − внутринуклонный процесс, в ядре распадается одиночный нуклон. При е-захвате ядро поглощает один из электронов атомной оболочки (обычно из K-оболочки), испуская нейтрино.
    Энергетические условия β-распада для масс атомных ядер.

β−-распад (n → p + e− + e) M(A,Z) > M(A,Z+1) + me,

(12)

β+-распад (p → n + e+ + νe) M(A,Z) > M(A,Z−1) + me,

(13)

     Энергия β-распада, выраженная через массы атомов M^ат(A,Z) имеет вид

     Энергетические диаграммы масс атомов M^ат(A,Z) , M^ат(A,Z−1) , M^ат(A,Z+1) при β^±-распаде и е-захвате показаны на рис. 6.

 Рис. 6. Энергетические диаграммы масс атомов (A,Z), (A,Z−1) и (A,Z+1) при β⁺‑распаде, e-захвате и β⁻‑распаде.

    Если масса исходного атома M^ат(A,Z) больше массы атома M^ат(A,Z−1) , но эта разность не превышает величину 2m_e , β⁺‑распад запрещен, а e-захват возможен.
    Энергии β-распада имеют широкий диапазон от 18.6 кэВ (³H → ³He + e⁻ + _e) до 13.4 МэВ
(¹²B → ¹²C + e⁻ + _e). Периоды β‑распада изменяются от 10^-6 с до 10¹⁷ лет.
    Бета-распады разделяются на разрешенные и запрещенные. К разрешенным β-переходам относятся переходы, при которых орбитальный момент, уносимый парой лептонов, l = 0. Порядок запрета β-распада определяется величиной орбитального момента l уносимой пары лептонов.

• l = 1 − запрещенные переходы первого порядка,
• l = 2 − запрещенные переходы второго порядка.

    Отношение вероятностей вылета пар лептонов с орбитальным моментом l и l = 0 равно

(18)

 где R − радиус ядра, − длина волны лептонов.

 Рис. 7. β-распад ядер-изобар с массовым числом A = 89.

    Правило Сарджента. При больших энерговыделениях Q_β вероятность β-распада λ ~ Q_β⁵.
    Взаимодействие атомного ядра с электронной оболочкой атома изменяет энергетические условия β-распада. Окруженное электронной оболочкой атомное ядро может быть стабильным и не распадаться в результате β-распада, в то время как ядро полностью лишенное электронной оболочки может испытывать β⁻-распад.
    Рассмотрим это на примере ядер-изобар ¹⁶³Dy и ¹⁶³Ho .

Рис. 8. Схема e-захвата в изотопе ¹⁶³Ho (слева) и полностью ионизованных атомах ¹⁶³Ho⁶⁷⁺ и ¹⁶³Dy⁶⁶⁺ (справа)

    Распад на связанное состояние атома был впервые обнаружен в 1992 г. Наблюдался β⁻-распад полностью ионизованного атома ¹⁶³Dy⁶⁶⁺ на связанные атомные состояния ¹⁶³Ho [H. Jung et al. Phys. Rev. Lett. 69 #15, 1992, p.2164]. Ядро ¹⁶³ Dy является стабильным ядром. Его основное состояние (5/2⁺) может заселяться в результате e-захвата из основного состояния (7/2 ⁺) ядра¹⁶³Ho. Ядро ¹⁶³Ho, окруженное электронной оболочкой, β⁻-радиоактивно и его период полураспада составляет
~10⁴ лет. Однако это справедливо, только если рассматривать ядро в окружении электронной оболочки. Для полностью ионизированных атомов картина принципиально другая. Теперь основное состояние ядра ¹⁶³Dy оказывается по энергии выше основного состояния ядра ¹⁶³Ho и открывается возможность для распада ¹⁶³Dy (рис. 8)

¹⁶³Dy⁶⁶⁺ → ¹⁶³Ho⁶⁷⁺ + e⁻ + _e.

Образующийся в результате распада электрон может быть захвачен на вакантную К или L-оболочку иона ¹⁶³Ho⁶⁷⁺.

¹⁶³Dy⁶⁶⁺ → ¹⁶³Ho⁶⁶⁺ + e⁻ + _e (в связанном состоянии)

Двойной β-распад

    Силы спаривания между тождественными нуклонами в ядре приводят к тому, что для четного массового числа A массы ядер-изобар описываются двумя параболами. Нижняя парабола описывает более устойчивые ядра с четным Z, а нижняя соответствует ядрам с нечетным Z.

Рис. 9. Массовые параболы ядер с четным массовым числом A.

В некоторых случаях ядро-изобар (A,Z±1) может обладать большей массой, чем ядра (A,Z) и (A,Z±2) , поэтому превращение ядра (A,Z) в более легкое ядро (A,Z±2) не может происходить путем двух последовательных β-распадов. В этих случаях превращение ядра (A,Z) в ядро-изобар (A,Z±2) может происходить с испусканием двух электронов или двух позитронов.

Рис. 10. Энергетическая диаграмма, поясняющая процесс
двойного β-распада.

Типы и энергии двойного β-распада приведены в таблице 2.

Таблица 2

Типы и энергии двойного β-распада

ε − энергия связи орбитального электрона.

    Двойной β-распад происходит в результате слабого взаимодействия.

Рис. 11. Ядра-изобары A = 130 ¹³⁰Te, ¹³⁰I, ¹³⁰Xe,  ¹³⁰Cs,  ¹³⁰Ba.

    На рис. 11 показаны β-распады ядер-изобар A = 130. Стабильный изотоп ¹³⁰Xe может образовываться как в результате β⁻-распада изотопа ¹³⁰I

¹³⁰I → ¹³⁰Xe + e⁻ + _e,

так и в результате β⁺-распада изотопа ¹³⁰Cs

¹³⁰Cs → ¹³⁰Xe + e⁺ + ν_e.

Изотоп ¹³⁰Xe может также образовываться как в результате 2β⁻-распада ¹³⁰Te, так и в результате 2β⁺ -распада ¹³⁰Ba.

¹³⁰Te → ¹³⁰Xe + 2e⁻ + 2_e,
¹³⁰Ba → ¹³⁰Xe + 2e⁺ + 2ν_e.

Таблица 3

Усредненные периоды  2β⁻-распада

Изотоп	Усредненные периоды полураспада (лет) по данным работ
	[R. Saakyan, Annu. Rev. Nucl. Part. Sci. 2013.63:503-529]	[A.S. Barabash, Nucl. Phys. A, 935 (2015) pp.52–64]
48Ca
76Ge		(1.65±0.4)·1021
82Se	(0.92±0.07)·1020	(0.92±0.7)·1019
96Zr	(2.35±0.21)·1019	(2.32±0.2)·1019
100Mo	(7.1±0.4)·1018	(7.1±0.4)·1018
100Mo(01+)
116Cd	(2.8±0.2)·1019	(2.87±0.13)·1019
128Te	(1.9±0.4)·1024	(2.0±0.3)·1024
130Te	(7.0±1.4)·1020	(6.9±1.3)·1020
136Xe	(2.30±0.12)·1021	(2.19±0.06)·1021
150Nd	(9.11±0.68)·1018	(8.2±0.9)·1018
150Nd(01+)
238U	(2.0±0.6)·1021	(2.0±0.06)·1021

    В таблице 3 приведены наиболее надежно измеренные периоды 2β⁻‑распада на основное состояние для 11 изотопов, проанализированные в работах [R. Saakyan, Annu. Rev. Nucl. Part. Sci. 2013.63:503-529] и [A.S. Barabash, Nucl. Phys. A, 935 (2015) pp.52–64]. Для изотопов ¹⁰⁰ Mo и ¹⁵⁰Nd измерены периоды полураспада на первое возбужденное состояние J^P = 0₁⁺.
    Двойной e⁻-захват был обнаружен на изотопе ¹³⁰Ba. Усредненное значение по данным измерений геохимическим методом приведено в таблице 4.

Таблица 4

2e⁻-захват на изотопе ¹³⁰Ba

Период полураспада, лет	Ссылка
(geochem.)	A.S. Barabash and R.R. Saakyan, Phys. At. Nucl. 59 (1996) 179.
(2.2±0.5)·1021 (geochem.)	A.P. Meshik, C.M. Hohenberg, O.V. Pravdivtseva, and Y.S. Kapusta, Phys. Rev. C 64 (2001) 035205.
(0.68±0.11)·1021 (geochem.)	M. Pujol. B. Marty, P. Burnard, and P. Philippot, Geoch. Cosm. Act.73 (2009) 6834.
Рекомендуемое значение: (2.2±0.5)·1021

Безнейтринный двойной β-распад

    Особый интерес представляют процессы двойного β-распада ядер без образования нейтрино в конечном состоянии – безнейтринный двойной β‑распад.

(A,Z) → (A,Z+2) + 2e⁻.

    В этом случае нейтрино, образовавшееся при β-распаде одного из нейтронов ядра (A,Z) взаимодействует с другим нейтроном образовавшегося ядра (A,Z+1). В результате рождаются 2 электрона, а заряд ядра увеличивается на две единицы (рис. 12). Такой процесс возможен в том случае, если нейтрино ν_e и антинейтрино _e являются тождественными частицами [Majorana E. – Nuovo cimento, 1937, v 14, p. 171] ν_e ≡ _e.

Рис. 12. Диаграмма Фейнмана безнейтринного двойного β-распада.

Рис. 13. Энергетический спектр электронов двойного β-распада ⁷⁶Ge.

    При двойном β-распаде без испускания нейтрино вся энергия 2β‑распада распределяется между двумя электронами, т.к. энергия ядра отдачи мала. Поэтому в суммарном спектре энергии двух электронов 0ν2β-распада должен наблюдаться узкий пик при энергии 2β-распада (рис. 13).
На рис. 13 показан теоретически рассчитанный спектр электронов, образующихся в реакции двойного β-распада изотопа ⁷⁶Ge в двух случаях.

• Двойной β-распад ⁷⁶Ge происходит с испусканием двух нейтрино (2ν2β).
   ⁷⁶Ge →⁷⁶Se + 2e⁻ + 2
  В этом случае суммарный спектр электронов непрерывный (0ν2β).
• Безнейтринный двойной β-распад.
  ⁷⁶Ge →⁷⁶Se + 2e⁻ + 2
  В этом случае суммарный спектр двух электронов монохроматический и равен энергии двойного β-распада.

Энергия двойного β-распада ⁷⁶Ge

Q(2ν2β)⁷⁶Ge = 2045.7 кэВ.

    Эти особенности спектров электронов используются при поиске безнейтринного двойного β-распада.
    Исследования двойного β-распада позволяют дать ответ на один из фундаментальных вопросов физики нейтрино: является нейтрино дираковской или майорановской частицей. Дираковское нейтрино существует в двух формах: нейтрино ν_e и антинейтрино _e. Майорановское нейтрино – симметричная частица – нейтрино тождественно антинейтрино.
    Если нейтрино является дираковской частицей, то при двойном β-распаде совместно с двумя электронам должно испускаться два антинейтрино. Расчёты Геперт-Майер (Phys. Rev. 48, 512, 1935) показали, что период полураспада в этом случае должен быть порядка 10²³ лет. Если нейтрино майорановская частица, то возможен двойной β-распад без испускания нейтрино.
    Двойной β-распад, в котором испускание двух электронов сопровождается испусканием двух антинейтрино является процессом разрешенным в рамках стандартной модели. Однако, т.к. это процесс второго порядка по константе слабого взаимодействия, он сильно подавлен. Характерные времена 2ν2β-распада составляют 10¹⁸–10²⁴ лет.
    Безнейтринный двойной β⁻-распад сопровождается испусканием только двух электронов. В этом распаде происходит нарушение закона сохранения лептонного числа L_e на две единицы. Однако такой процесс может происходить для майорановского нейтрино ν_e ≡ _e с массой отличной от нуля.
    Исследование безнейтринного двойного β-распада

• является одним из наиболее чувствительных методов проверки закона сохранения лептонного числа L_e ;
• позволяет получить информацию о природе массы нейтрино, абсолютную шкалу массы нейтрино;
• позволяет получить информацию о существовании правых токов в электрослабых взаимодействиях.

    Несмотря на многочисленные экспериментальные попытки, безнейтринный двойной β-распад не обнаружен. Были получены лишь оценки периода полураспада безнейтринного двойного β-распада. В таблице 5 приведено сравнение экспериментальных результатов по периодам полураспада двойного β-распада и безнейтринного 2β-распада некоторых изотопов.

Таблица 5

Периоды полураспада T_1/2(2ν2β) и T_1/2(0ν2β) некоторых изотопов

Гамма-переходы в ядрах

    Явление γ-излучения ядер состоит в том, что ядро (A,Z) испускает γ-квант без изменения массового числа А и заряда ядра Z. Испускание γ-излучения обычно происходит после α- или β-распадов атомных ядер, если образовавшееся ядро образуется в возбужденном состоянии.
    Гамма-излучение возникает при распаде возбужденных состояний ядер. Спектр γ-излучения всегда дискретен из-за дискретности ядерных уровней. С точностью до незначительной энергии отдачи ядра энергия γ-перехода равна разности энергий уровней, между которыми происходит γ-переход.
    Гамма-излучение ядер обусловлено взаимодействием нуклонов ядра с электромагнитным полем. В отличие от β-распада, γ-излучение − явление не внутринуклонное, а внутриядерное. Изолированный свободный нуклон испустить или поглотить γ-квант не может из-за совместного действия законов сохранения энергии и импульса. В то же время внутри ядра нуклон может испустить γ-квант, передав при этом часть импульса другим нуклонам.
    Времена жизни γ-радиоактивных ядер обычно изменяются от 10 ^-8 с до 10^-17 с, т. е. в среднем они значительно меньше времен жизни по отношению к α- и β-распадам. Причина в том, что интенсивность электромагнитных взаимодействий всего лишь на три порядка слабее ядерных. Время жизни γ-радиоактивных ядер зависит от различия спинов и четностей начального и конечного состояний, между которыми происходит γ-переход.
    Гамма-переходы происходят между ядерными состояниями, характеризующимися определенными значениями спина J_i, J_f и чётности P_i, P_f. Поэтому γ-кванты также имеют определённые значения спина J_γ и четности P_γ. Законы сохранения момента количества движения J и четности P в электромагнитных переходах

или |Ji − Jf| ≤ Jγ ≤ Ji + Jf

(23)

определяют спин  J_γ и четности P_γ, уносимую γ-квантом.

    Обычно используется классификация γ-квантов по полному моменту количества движения J и четности P. Полный момент количества движения γ-кванта J принимает целочисленные значения:
J = 1, 2, 3, ... Значение J = 0 для γ-кванта исключено, так как оно отвечает сферически симметричному состоянию, а электромагнитная волна поперечна. Число J называется мультипольностью γ-кванта. Низшие мультиполи имеют следующие названия: диполь − J = 1, квадруполь − J = 2, октуполь − J = 3. Спин γ-кванта J равен 1,

    В зависимости от чётности при определенном значении полного момента J γ-кванты различают по типу на магнитные и электрические:

    Вероятности вылета (или поглощения) магнитных и электрических фотонов подчиняются следующим приближенным соотношениям

(28)

(29)

Рис. 14. Вероятности протонных γ-переходов (в с^-1) в зависимости от энергии γ-квантов различных мультипольностей.

Ядерная изомерия

    Времена жизни γ-радиоактивных ядер обычно имеют порядок 10 ^-8–10^-17 с. В некоторых случаях при сочетании высокой степени запрета с малой энергией γ-перехода могут наблюдаться γ‑радиоактивные ядра с временами жизни макроскопического порядка (до нескольких часов, а иногда и больше). Такие долгоживущие возбужденные состояния ядер называются изомерами. Характерным примером изомера может служить изотоп индия ¹¹⁵In (рис. 15). Основное состояние ¹¹⁵In имеет J^P = 9/2⁺. Первый возбужденный уровень имеет энергию, равную 335 кэВ, и спин-четность J^P = 1/2⁻. Переход между этими состояниями происходит посредством испускания М4 γ‑кванта. Этот переход настолько сильно запрещен, что период полураспада возбужденного состояния оказывается равным 4.5 часа.

Рис. 15. Изомерный γ-переход в ядре ¹¹⁵In.

    Изомерные состояния следует ожидать там, где оболочечные уровни, близкие друг другу по энергии, сильно различаются значениями спинов. Именно в этих областях и находятся так называемые «острова изомерии». Наличие изомера у приведенного выше изотопа ¹¹⁵In обусловлено тем, что в нем не хватает одного протона до замкнутой оболочки Z = 50, т. е. имеется одна протонная «дырка». В основном состоянии эта дырка в подоболочке 1g_9/2, а в возбужденном − в подоболочке 1p_1/2. Острова изомерии расположены непосредственно перед магическими числами 50, 82 и 126 со стороны меньших Z и N. В настоящее время обнаружено большое число изомеров, имеющих период полураспада от нескольких секунд до 3·10⁶ лет (^210mBi). Многие изотопы имеют несколько изомерных состояний. В таблице 6 приведены долгоживущие изомеры с T_1/2 > 1 год.

Таблица 6

Параметры изомерных состояний атомных ядер

Рис. 16. Низколежащие изомерные состояния ²²⁹Th.

    Изотоп ²²⁹Th имеет изомерное состояние, расположенное при энергии ≈8 эВ. Это самое низкорасположенное из всех известных изомерных состояний. Энергия изомерного состояния измерялась, используя различные каналы распада возбужденного состояния 7/2⁺ E* = 71.82 кэВ, которое заселялось в результате α-распада изотопа ²³³U

²³³U → ²²⁹Th + α.

Распад изомерного состояния происходит в результате испускания М1 фотонов. Оцененный период полураспада изомерного состояния ≈5 час.

Внутренняя конверсия γ-квантов

    Атомное ядро, находящееся в возбужденном состоянии, может в результате взаимодействия с электронами атомных оболочек передать энергию возбуждения непосредственно электрону − внутренняя конверсия γ‑квантов. С наибольшей вероятностью внутренняя конверсия происходит на электронах ближайших к ядру K- и L-оболочек. Электрон вылетает из атома с кинетической энергией E_e.

где E* − энергия возбуждения ядра, I_{связи е} − энергия связи электрона на соответствующей оболочке атома.
    Из соотношения (30) следует, что спектр электронов внутренней конверсии дискретный в отличие от спектра электронов β-распада. Вероятность внутренней конверсии уменьшается с увеличением энергии возбуждения ядра и увеличивается с увеличением мультипольности γ‑перехода в ядре и увеличением заряда ядра Z. Измерение энергии конверсионных электронов даёт информацию о возбужденных состояниях ядер – их энергии, спине и четности. Испускание электронов внутренней конверсии сопровождается характеристическим рентгеновским излучением.

Деление атомных ядер

    Деление атомных ядер − распад ядра на два (реже три) сравнимых по массе осколка. Деление энергетически выгодно для тяжелых ядер. Если начальное ядро массы M(A,Z) , состоящее из Z протонов и N нейтронов, делится на два осколка, имеющие массы M₁(A₁,Z₁) и M₂(A₂,Z₂) , массовые числа A₁ и A₂ и заряды Z₁ и Z₂ , то энергия деления Q_дел определяется соотношением

    Зависимость периоды полураспада спонтанно делящихся изотопов Z = 92–100 от параметра делимости Z₂/A показана на рис. 17.

Рис. 17. Периоды полураспада спонтанно делящихся изотопов Z = 92–100.

Рис. 18. Массовое распределение осколков деления.

    Характерной особенностью деления является то, что осколки деления, как правило, существенно различаются по массам, т. е. преобладает асимметричное деление. Так, в случае наиболее вероятного деления изотопа урана ²³⁶U, отношение масс осколков равно 1.46. Тяжёлый осколок имеет массовое число 139 (ксенон), а легкий – 95 (стронций). С учётом испускания двух мгновенных нейтронов рассматриваемая реакция деления имеет вид

n + ²³⁵U → ²³⁶U → ⁹⁵Sr + ¹³⁹Xe + 2n .

    Осколки деления образуются в широком диапазоне массовых чисел A = 72–161 и зарядов ядер
Z = 30–65.
    Асимметричное деление объясняется влиянием оболочечной структуры ядра: ядро стремится разделиться так, чтобы основная часть нуклонов каждого осколка образовала устойчивый магический остов.
    При наиболее вероятном делении отношение массовых чисел А и зарядов Z лёгкого и тяжёлого осколков связаны соотношениями

Рис. 19. Зависимость средних масс легкой и тяжелой групп осколков от массы делящегося ядра.

    С увеличением массового числа A делящегося изотопа тяжелая группа изотопов, соответствующая образованию изотопов вблизи массового числа 138 (Z ≈ 50, N ≈ 82) не изменяется, в то время как массовое число легкой группы изотопов растет с ростом A.
    Процесс деления атомных ядер удобно описывать в рамках капельной модели ядра. В процессе деления происходит увеличение поверхностной энергии делящегося ядра и уменьшение кулоновской энергии ядра. Зависимость поверхностной, кулоновской энергий и их суммы в случае деления изотопа ²³⁶U на два осколка ¹⁴⁰Xe и ⁹⁶Sr показана на рис. 20.
    Если ядро делится на два равных осколка, то деление оказывается энергетически выгодным, если Z²/A > 17. Величина Z²/A называется параметром деления.

Рис. 20. Зависимость поверхностной и кулоновской энергий осколков деления и их суммы от расстояния между центрами осколков для наиболее вероятного варианта деления ²³⁶U. Точка 12 Фм на оси расстояний отвечает сумме радиусов сферических осколков Хе и Sr.

Рис. 21. Зависимость формы и высоты потенциального барьера, а также энергии деления от величины параметра Z²/А. Двусторонняя вертикальная стрелка показывает высоту барьера деления.

Так как для стабильных изотопов отношение N/Z увеличивается с увеличением массового числа A , осколки деления оказываются перегружены нейтронами. Поэтому при делении образуются 2 – 4 мгновенных нейтрона, что уменьшает отношение N/Z в осколках. Дальнейшее продвижение осколков к стабильным ядрам происходит путем последовательных β⁻-распадов. Так, например, цепочка последовательных распадов изотопа ⁹⁷Kr образующегося при делении ²³⁶U претерпевает 6 последовательных распадов до образования стабильного изотопа ⁹⁷Mo .

    Согласно капельной модели атомные ядра, имеющие отношение N/Z > 49, должны делиться в течение характерного ядерного времени τ ≈ 10⁻²³ сек, т.к. в этих ядрах исчезает барьер деления. Возможно как спонтанное деление ядра, так и деление ядер под действием нейтронов, фотонов, протонов и других частиц. В результате деления выделяется энергия ≈ 200 МэВ. В таблице 7 приведено распределение энергии деления ядра ²³⁵U тепловыми нейтронами.

Таблица 7

Распределение энергии деления ²³⁵U тепловыми нейтронами

Кластерная радиоактивность

    Явление кластерной радиоактивности состоит в том, что атомное ядро самопроизвольно распадается с испусканием более тяжелых фрагментов, чем α-частицы. Пример кластерной радиоактивности

²²³Ra → ¹⁴C + ²⁰⁹Pb + 31.85 МэВ.

    Решающим фактором, который привел к открытию кластерной радиоактивности, был выбор распадающегося изотопа. Максимальный выигрыш в энергии получается в том случае, если в результате кластерного распада образуется изотоп близкий к дважды магическому изотопу ²⁰⁸Pb. При этом повышается вероятность прохождения кластера через потенциальный барьер, что увеличивает вероятность распада с образованием определенного кластера. Спонтанный вылет ядер ¹⁴C обнаружен в изотопах ²²¹Fr, ²²¹Ra, ²²²Ra. В настоящее время известно свыше 10 изотопов, для которых обнаружена кластерная радиоактивность. Наряду с испусканием ядер ¹⁴C наблюдалось испускание ядер ²⁴Ne, ²⁶Ne, ²⁸Mg, ³²Si.
    Отношение вероятности испускания кластера к вероятности испускания α-частицы варьируется в интервале ~10^-10–10^-13. Однако в отдельных случаях, например, в случае испускания изотопов ^28,30Mg оно может доходить до 10^-17.
    Так же как и в случае с α-распадом одним из главных факторов является энергия распада. Многие тяжелые ядра оказываются энергетически неустойчивы к распаду на два ядра A → A₁ + A₂

Q = [M(A) – M(A₁) – M(A₂)]c²,

т.е. величина Q оказывается положительной для большого числа различных комбинаций A₁и A₂. Однако только некоторые сочетания массовых чисел A₁ и A₂ оказываются сильно выделены, и при распаде образуются именно эти сочетания. Сильное влияние на энергию распада оказывают замкнутые оболочки.

Рис. 22. Зависимость логарифма парциального периода кластерного распада от логарифма проницаемости кулоновского потенциального барьера

    На рис. 22 показана зависимость логарифма парциального периода кластерного распада от логарифма проницаемости потенциального барьера. Для сравнения здесь же приведена аналогичная зависимость α‑распада.

Протонная радиоактивность

    Протонная радиоактивность должна наблюдаться для протоноизбыточных изотопов, расположенных вблизи границы с нулевой энергией отделения протонов B_p = 0.
    В таблице 8 приведены изотопы Tu (Z = 69) и Lu (Z = 71), на которых впервые наблюдалось испускание протонов из основного состояния. В ряде случаев наблюдается конкуренция каналов распада с испусканием протонов, β⁺-распада и α-распада.

Таблица 8

Распады протоноизбыточных изотопов Tu (Z = 69) и Lu (Z = 71)

    В настоящее время известно ~40 изотопов, в которых наблюдалась протонная радиоактивность. Они расположены в области ядер с Z < 80. В области больших Z в районе границы B_p = 0 доминирует
α-распад.

Рис. 23. Протонная радиоактивность изомерного состояния ^53mCo.

Испускание протонов из изомерного состояния 19/2^– с энергией 3.119 МэВ было обнаружено на изотопе ⁵³Co (рис. 23). Наблюдалось испускание протонов с энергией 1.59 ± 0.03 МэВ. Период полураспада T_1/2 = 243±15 мс. Основным каналом распада изомерного состояния ^53mCo является β⁺-распад. Доля распадов с испусканием протонов составляет 1.5%, что соответствует парциальному периоду полураспада с испусканием протонов ~16 с.
    Изомерные состояния наиболее часто образуются в результате предшествующего β-распада. Для того, чтобы наблюдалось испускание протонов из изомерного состояния необходимо выполнение двух условий.

• Энергия возбужденного ядра (A,Z) в изомерном состоянии должна быть больше энергии отделения протона в этом ядре.
• Испускание протонов из изомерного состояния должно происходить быстрее, чем γ-переход из этого изомерного состояния.

Нейтронная радиоактивность

    С правой стороны N-Z диаграммы за стабильными ядрами располагаются нейтроноизбыточные ядра. Эта область недостаточно исследована. В этой области располагаются ~ 3 тысячи ядер, существование которых предсказывают ядерные модели, но которые пока не обнаружены.
    Для нейтроноизбыточных легких ядер, расположенных на границе нейтронной радиоактивности (neutron drip-line) наблюдается распад ядра (A,Z) из основного состояния с испусканием нейтронов. При этом массовое число A уменьшается на единицу, заряд ядра не изменяется.

    Число обнаруженных нейтронорадиоактивных ядер ~20.
    Нейтронную радиоактивность обнаруживают все тяжелые изотопы лёгких ядер с Z = 1 (^4,5,6H) и
Z = 2 (^5,7,9,10He). Нейтронная радиоактивность наблюдается вплоть до изотопов с Z = 16. Нейтронными излучателями являются тяжелые изотопы ²⁶O, ³³Ne, ³⁶Na, ³⁹Mg и ⁴⁹S.
    Увеличение вероятности испускания нейтронов с ростом числа нейтронов в ядре обусловлено увеличением энергии симметрии

с ростом числа нейтронов в нейтроноизбыточных ядрах.
    В отличие от протонной радиоактивности в случае нейтронной радиоактивности период полураспада с испусканием нейтрона определяется в основном орбитальным моментом, уносимым нейтроном. Для нейтронов не существует кулоновский потенциальный барьер, но существует центробежный потенциальный барьер.
    В таблице 9 приводятся массовые числа стабильных изотопов и массовое число изотопа, для которого обнаружена нейтронная радиоактивность.

Таблица 9

Граница обнаруженных изотопов излучателей нейтронов

    Различие в величинах энергии отделения одного нейтрона B_n и энергии отделения двух нейтронов, обнаруженное для легких ядер, свидетельствует о том, что следует говорить о нейтронном drip-line B _n = 0 и двух нейтронном drip-line B_2n = 0. Практически для всех легких ядер стабильность уменьшается при добавлении двух нейтронов. Для изотопов He это правило не соблюдается (так называемая «гелиевая аномалия» (рис. 24). Наибольшее увеличение энергии связи с увеличением числа нейтронов (~1.2 МэВ) наблюдается для изотопов ⁶ He –⁸He. Аналогичная ситуация имеет место для изотопов ⁵He–⁷He (~0.5 МэВ). Даже добавление четырех нейтронов к ядру ⁵He существенно не изменяет энергию связи.

Рис. 24. Энергия связи одного и двух нейтронов в изотопах He
(«гелиевая аномалия»).

Сверхтяжелые элементы

    Ограничение на существование атомных ядер существует и со стороны сверхтяжелых элементов. Самыми тяжелыми стабильными изотопами являются изотопы свинца ^{204, 206, 207, 208}Pb (Z = 82) и висмута ²⁰⁹Bi (Z = 83), расположенные вблизи магических чисел Z = 82, N = 126. Все изотопы с Z > 83 являются радиоактивными. Изотопы урана и тория, которые сохранились на Земле со времени образования Солнечной системы и их последующий распад проводят к образованию химических элементов с Z = 82–91 (табл. 10).

Таблица 10

Долгоживущие изотопы урана U и тория Th

    Периоды полураспада наиболее долгоживущих изотопов Z = 83–89 не превышает 2·10³ лет. Изотопы урана и тория образуют полуостров стабильности − группу долгоживущих изотопов, окруженную «морем радиоактивности». Все химические элементы тяжелее урана − трансурановые элементы — были получены на Земле в лабораторных условиях в различных ядерных реакциях.

Таблица 11

Химические элементы Z > 83.

Для каждого элемента приведены год открытия и реакция,
в которой химический элемент был получен, а также массовое число A и период полураспада T_1/2 наиболее долгоживущего из известных изотопов

Год откр.	Символ элемента	Реакция образования	A	T1/2 [26]
1789	92U	Радиохимическая идентификация изотопов, существующих в природе	238	(4.468 ± 0.003) · 109 л
1898	88Ra		226	1600 ± 7 л
1898	90Th		232	(1.40 ± 0.01) · 1010 л
1898	84Po		209	102 ± 5 л
1899	86Rn		222	3.8235 ± 0.0003 д
1899	89Ac		227	21.772 ± 0.003 л
1913	91Pa		231	(3.276 ± 0.011) · 104 л
1939	87Fr		223	22.00 ± 0.07 м
1940	85At		210	8.1 ± 0.4 ч
1940	93Np		237	(2.144 ± 0.007) · 106 л
	94Pu		244	(8.00 ± 0.07) · 107 л
1945	95Am		243	7370 ± 40 л
1944	96Cm		247	(1.56 ± 0.05) · 107 л
1949	97Bk		247	1380 ± 250 л
1950	98Cf		251	898 ± 44 л
1952	99Es		252	471.7 ± 1.9 д
1952	100Fm		257	100.5 ± 0.2 д
1955	101Md		258	51.5 ± 0.3 д
1961	103Lr		262	~ 4 ч
1963	102No		259	58 ± 5 м
1964	104Rf		263	10 ± 2 м
1970	105Db		268m
1974	106Sg		271m
1981	107Bh		274
1984	108Hs		270	22 с
1982	109Mt		278m
1994	110Ds		281
1994	111Rg		281m
1996	112Cn		285
2004	113Nh		286m
1999	114Fl		289m
2004	115Mc		289
2000	116Lv		293
2010	117Ts		294
2006	118Og		294

    Химическим элементом, имеющим максимальное Z, является химический элемент Оганесон Z = 118. На рис. 25 показан верхний участок N-Z диаграммы атомных ядер, обнаруженных к 2016 г. Согласно расчетам в районе Z = 114, N = 183 возможно существование изотопов, имеющих периоды полураспада T_1/2 ≈ 10³ – 10⁵ лет. Синтезированные в настоящее время изотопы уже превысили ожидаемое значение Z = 114. Однако все полученные изотопы имеют число нейтронов гораздо меньше N = 184. Косвенным подтверждением существования острова стабильности являются увеличение периодов полураспада с увеличением числа нейтронов в изотопах с Z = 113–116. Для достижения острова стабильности необходимо использовать реакции с мишенями и пучками налетающих ускоренных ионов с большим отношением N/Z.
    Основными каналами распада сверхтяжелых элементов является α-распад и деление ядер. Эффективным методом идентификации сверхтяжелых элементов является идентификация цепочек последовательных α-распадов. На рис. 26 показаны цепочки последовательных распадов изотопов нихония (Z = 113), московия (Z = 115) и теннессина (Z = 117), измеренные в ЛЯР ОИЯИ.

Рис. 25. Известные к 2016 году изотопы сверхтяжелых элементов и реакции их образования. Для каждого изотопа указаны название элемента, его масса и период полураспада. Нейтрон-дефицитные тяжелые изотопы с Z ≤ 113 были получены в реакциях «холодного слияния».
Изотопы 112–118 с большим числом нейтронов образованы в реакциях «горячего слияния».

Рис. 26. Цепочки распадов изотопов ²⁸²113, ^{287, 288, 289}115 и ^{293, 294}117, полученных в ЛЯР ОИЯИ. Для каждого изотопа указаны время жизни и энергия α-распада E_α (МэВ). Внизу цепочек указано число событий и год публикации.

Радиоактивные изотопы. Научные проблемы. Практические приложения

Рис. 27. Основные направления исследований с помощью пучков радиоактивных ядер.

    Изучение радиоактивных атомных ядер позволяет получить новую информацию о свойствах атомных ядер и использовать её в практических приложениях.

• Изучить область существования атомных ядер. С этой целью исследуются наиболее тяжелые из полученных в настоящее время сверхтяжелых ядер. Исследуются ядра вблизи границ энергий отделения протона B_p = 0 и нейтрона B_n = 0, что позволяет ответить на вопрос, существуют ли компактные области устойчивых ядер вне этих границ, каковы возможные причины существования таких областей.
• Существуют ли в области экзотических ядер те же магические числа, как и для ядер долины стабильности? Ответ на этот вопрос особенно важен, т.к. позволит получить дополнительную информацию о форме атомных ядер и, в частности, о супердеформированных ядрах в основном состоянии. До сих пор супердеформированнные ядра были обнаружены лишь в возбужденных состояниях. Для экзотических ядер возможно появление новых магических чисел, обусловленное сильно деформированными состояниями.
• Исследовать изменение свойств атомных ядер в том случае, когда соотношение между числом нейтронов и протонов отличается от равновесных значений для ядер долины стабильности. В настоящее время твердо установлено существование нейтронного гало и нейтронного слоя у легких нейтроноизбыточных ядер. Протонное гало обнаружено в изотопах ⁸ B, ¹⁷F, ¹⁷Ne. Нейтронное гало обнаружено в изотопах¹¹Be, ¹⁹C. Двухнейтронное гало обнаружено на изотопах ⁶He, ¹¹Li, ^{12, 14}Be, ¹⁷B. Изотоп ⁸He имеет структуру α + 4n.
• Исследовать различие распределений плотности протонов и нейтронов в экзотических ядрах с сильно неравновесным отношением N/Z, распределение масс и зарядов в экзотических ядрах.
• Изменение величины спин-орбитального взаимодействия с изменением величины N/Z.
• Исследовать существование нейтронного гало в возбужденных состояниях ядер
• Исследовать существование эффектов кластеризации ядерных состояний в области малой нейтронной плотности?
• Исследовать форму атомных ядер в областях с различными значениями N/Z.
• Основными модами радиоактивного распада ядер вблизи долины стабильности являются α-,
  β-распады и γ-переходы, при приближении к границам нуклонной стабильности изменяется энергия Ферми для протонов и нейтронов. Вследствие этого появляются новые моды распада - испускание запаздывающих нейтронов, протонов, дейтронов, тритонов и испускание двух и трех нейтронов из возбужденных состояний ядер, образующихся в результате предшествующего β-распада.
• Изменение представлений об эволюции Вселенной с появлением новой информации о свойствах экзотических ядер. Траектория r‑процесса проходит по области атомных ядер, сильно перегруженных нейтронами.
• Наиболее эффективным использованием физики деления атомных ядер является строительство ядерных реакторов. В настоящее время в мире работает » 440 ядерных реакторов, которые производят 370 ГВт электроэнергии.
• Энергия ядерных взрывов используется при строительстве подземных хранилищ нефти и газа.
• Радиоактивные изотопы широко используются в медицине при анализе различных заболеваний и лечении.
• Радиоактивные изотопы используются при стерилизации различных изделий.
• В машиностроении радиоизотопы используются при измерении толщин различных изделий и обнаружения дефектов.
• В химии и биологии радиоизотопы используются для определения механизмов и скоростей различных реакций и процессов.
• · Радиоуглеродный метод геохронологии широко используется в археологии и геологии при определении возраста земных пород.
• Для датировки горных пород широко используется метод датировки по урану и свинцу и рубидий-стронциевый метод.
• Поглощение испущенных заряженных частиц в результате радиоактивного распада используют при создании радиоизотопных источников энергии.

Таблица 12

Радиоизотопы - источники энергии

Используя термоэлементы энергию распада можно непосредственно превращать в электроэнергию. Радиоизотопные генераторы энергии используются на спутниках, метеостанциях.

• Ядерные источники энергии используются в атомных ледоколах, подводных лодках.
• Использование ядерных ракет имеет ряд преимуществ перед ракетами на химическом топливе, позволяет выводить на орбиты больший груз и совершать длительные космические экспедиции.
• Метод активационного анализа позволяет определить, какие химические элементы находятся в образце. Содержание исследуемого радиоактивного изотопа может быть получено с точностью 10⁻⁷ – 10⁻⁸.
• Радиоизотопы широко используются в контроле уровня загрязнения окружающей среды.
• Метод мессбауэровской спектроскопии используется в физике твердого тела, во многих областях химии. Метод меченых изотопов имеет ряд преимуществ перед другими методами благодаря высокой чувствительности и избирательности.

Литература

1. М. Кюри. «Радиоактивность».

2. Э. Резерфорд. «Нуклеарное строение атома», УФН, Т. II, вып.2, с. 194–221 (1921).

3. C.F.Von Weizsaker. Z. Phys. 96 (1935) 431.

4. Б.С. Ишханов, И.М. Капитонов, Н.П. Юдин. «Частицы и атомные ядра». Москва, 2007.

5. К.Н.Мухин. Экспериментальная ядерная физика, -М., Энергоатомиздат, 1993.

6. М.Goeppert-Mayer. Phys. Rev. 75 (1949) 1464.

7. М.Гепперт-Майер, И.Г.Д.Йенсен. Элементарная теория ядерных оболочек. –М., Наука, 1958.

8. Б.С.Ишханов, Э.И.Кэбин. Экзотические ядра. –М., Издательство Московского университета, 2002.

9. Методы определения основных характеристик атомных ядер и элементарных частиц. -М., Наука, 1965.

10. В.В.Варламов, Б.С.Ишханов, С.Ю.Комаров Атомные ядра. Учебное пособие. ISBN 978-5-91304-122-72010. –М., Университетская книга, 2010.

11. База данных ЦДФЭ НИИЯФ МГУ «Параметры основных и изомерных состояний атомных ядер», URL: ( http://cdfe.sinp.msu.ru/services/gsp.ru.html ).

12. Nuclear Wallet Cards, USA National Nuclear Data Center – NNDC, URL: http://www.nndc.bnl.gov/wallet/wccurrent.html .

13. C.M. Lederer, J.M. Hollander, and I. Perlman, “Table of Isotopes”, John Wiley and Sons, New York (1967).

14. «Бета- и гамма-спектроскопия». Под редакцией К. Зигбана. Москва, 1959.

15. Р. Колиакчиева, Ю.Э. Пениончикевич, Х.Г. Болен. Сильнонейтроноизбы­точ­ные изотопы лёгких ядер. Физика элементарных частиц и атомного ядра, Т. 29, вып.4, с. 832 (1998), т. 30, вып.6, с. 1429 (1999).

16. О. Бор, Б. Моттельсон. «Структура атомного ядра». Москва, 1971.

17. Wolfram Alpha. Распад радиоактивных ядер. http://www.wolframalpha.com

18. Б. С. Ишханов. Двойной бета-распад. Учен. зап. физ. фак-та Моск. ун-та. 2016. № 2. 162201

19. Б. С. Ишханов. Двухпротонная радиоактивность. Учен. зап. физ. фак-та Моск. ун-та. 2015. № 2. 152202