|
Закон сохранения энергии в с.ц.и.
можно записать в следующем виде:
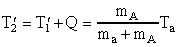 , ,
|
(k.3) |
где T'1 и T'2- суммарные кинетические
энергии в с.ц.и. в начальном и конечном
состояниях. Для импульсов можно записать:
где 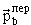 и и 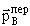 -
импульсы переносного движения, -
импульсы переносного движения, 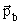 , ,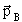 , , 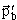 , , 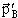 -импульсы частиц b и B в л.с. и
в с.ц.и., -импульсы частиц b и B в л.с. и
в с.ц.и.,
 bB = mbmB/(mb+
mB) - приведенная масса. bB = mbmB/(mb+
mB) - приведенная масса.
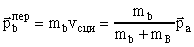 , , |
(k.7) |
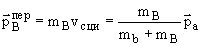 , , |
(k.8) |
где vсци - скорость центра инерции. То есть
переносные импульсы получаются делением
импульса  a пропорционально массам частиц,
образующихся в конечном состоянии. a пропорционально массам частиц,
образующихся в конечном состоянии.
Комбинируя (k.3) и (k.6) получим
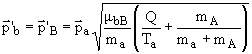
|
(k.9) |
Импульсы и углы вылета частиц b и B,
образующихся в конечном состоянии можно
определить c помощью импульсной диаграммы
ядерной реакции.
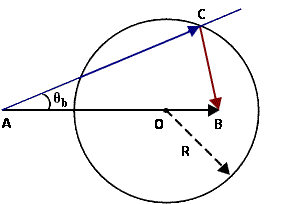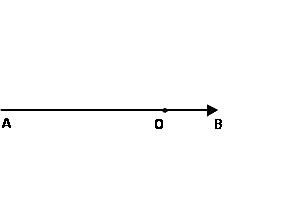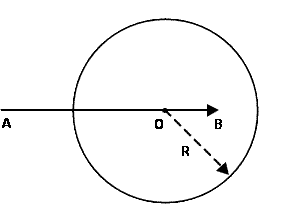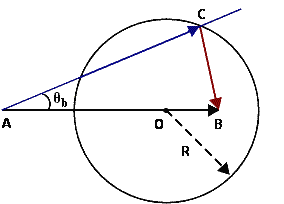 |
| Рис. k1. Импульсная диаграмма реакции |
Диаграмма строится следующим образом (рис. k1):
- Импульс налетающей частицы |
 a| = AB делится пропорционально
отношению масс частиц продуктов mb/mB в
точке O. a| = AB делится пропорционально
отношению масс частиц продуктов mb/mB в
точке O.
- Из точки O деления импульса |
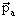 | = AB проводится
окружность с радиусом | | = AB проводится
окружность с радиусом |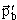 |
= | |
= |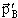 | = OC. | = OC.
- Откладываются известный из условия задачи угол
(как правило из трех углов
 b, b,  'b, 'b,  B один известен). B один известен).
|