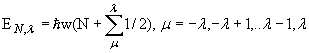3.3. Модель коллективных ядерные колебаний

    Одночастичная модель оболочек (ОМО) частично объясняет спины и четности уровней в спектрах ядерных возбуждений, но интерпретация многих свойств возбужденных ядер остается за пределами ее возможностей. К таким свойствам относятся, например, спектры возбуждения многих четно- четных ядер. В спектрах возбуждения ядер присутствуют как те возбужденные состояния, которые можно считать результатов перехода одной или нескольких квазичастиц с одного уровня на другой, так и те, которые можно интерпретировать как коллективные возбуждения ядра как целого. К этому типу ядерных возбужденных состояний относятся те, которые возникают вследствие коллективных колебаний ядерной “капли” как целого. Эти колебания проявляются, например, в изменениях формы ядерной поверхности. Наиболее существенными среди колебаний формы являются квадрупольные и октупольные колебания (см. рис.7.15 в [2]). Теоретическое изучение коллективных колебаний показывает, что этот тип ядерных возбуждений можно рассматривать как результат поглощения ядром кванта коллективных колебаний - фонона. Спектр энергий, соответствующий поглощению ядром одного, двух и т.д. фононов в первом приближении эквидистантный (напомним, что решение задачи о квантовом осцилляторе всегда приводит к эквидистантному спектру энергий). В спектрах низкоэнегетических возбужденных состояний большинства сферических (и близких к сферическим) ядер видны уровни, соответствующие поглощению одного и двух квадрупольных фононов. Например, спектры низших возбужденных состояний четно-четных ядер ⁶⁰Ni, ¹⁰⁶Pd (см.стр.35 в [1]) являются типичными примерами одно- и двухфононных квадрупольных колебаний. Поглощению одного фонона с моментом 2⁺ соответствуют низшие возбужденные состояния этих ядер. Последовательное поглошение двух квадрупольных фононов могло бы дать в результате спин возбужденных состояний:

     Однако правила отбора исключают значения 1 и 3, что дает для спинов возбужденных состояний с двумя квадрупольными фононами значения 0,2,4, которые и наблюдаются экспериментально.
    Энергии возбуждения для коллективных гармонических колебаний с моментом фонона равны

Для квадрупольных фононов = 2, а проекция спина фонона на выделенную ось пробегает 5 значений. Поэтому спектр квадрупольных гармонических колебаний имеет вид
E_N,=2 = (N + 5/2). Энергия одного кванта   коллективных гармонических колебаний зависит от характеристик данного ядра. Энергия кванта тем выше, чем больше так называемая “жесткость” ядра. Для ядер с замкнутыми оболочками или подоболочками “жесткость” и, соответственно, энергия кванта  выше, чем для ядер с незамкнутыми валентными оболочками. На приведенном выше примере ядро ⁶⁰N является “магическим” по протонам (Z = 28). Валентная нейтронная подоболочка этого ядра также замкнута и соответствует конфигурации (2p_3/2)⁴. Поэтому и энергии квадрупольных фононных возбуждений этого ядра примерно вдвое выше, чем у ядра ¹⁰⁶Pd

3.4. Вращательные спектры ядер

    Несферические ядра, помимо колебательных уровней в спектре возбуждения и уровней, связанных с переходами нуклонов ядра на более высокие оболочки, имеют также уровни в спектрах возбуждения, которые имеют вращательную природу.
    Уровни спектров возбуждения, возникающие вследствие вращения несферических ядер, имеют ряд характерных особенностей; последовательность таких уровней часто называют вращательной полосой. Два примера таких вращательных полос для четно- четных ядер показаны на стр.34 [1] для ¹⁸⁰Hf и ¹⁶⁰Dy.
    Энергии уровней вращательной полосы можно получить в результате решения у.Ш. с гамильтонианом, отражающим вращательные степени свободы ядра. Следует подчеркнуть, что, согласно квантовой теории, вращательные степени свободы присущи исключительно несферическим объектам. При обсуждении квадрупольных моментов ядер было показано, что вытянутые ядра имеют положительный квадрупольный момент, а сплюснутые - отрицательный. Прямое измерение электрических квадрупольных моментов возможно лишь для ядер, у которых спин больше или равен 1. Однако многие четно-четные ядра, имеющие спин и четность 0⁺ , являются деформированными, и их деформация проявляется в спектрах их возбужденных состояний в виде вращательных полос. Вид вращательного гамильтониана легко получить из принципа соответствия классических и квантовых величин. В классической физике энергия тела с моментом инерции и моментом количества
движения J:   E_rot = J²/(2).

В квантовой физике величине J² соответствует оператор квадрата момента, действующий на волновую функцию ядра. Поскольку в принятой системе обозначений спин ядра и частиц измеряется в единицах , то

Формула, связывающая энергию вращательного уровня и спина состояния, приближенно описывает ход уровней во вращательной полосе.

В таблице даны также интервалы энергий Е между данным уровнем и низшим по энергии. Соотношение для интервалов энергий уровней вращательной полосы, спинов уровней и соответствующих этим состояниям моментов инерции ядра может быть получено из (3.29):

Таблица.
Спины, энергии, интервалы энергий и моменты инерции состояний вращательной полосы ядра ¹⁷⁰Hf.

Обычно в физике ядра рассчитывают не момент инерции ядра в том или ином состоянии, а величину
 = 2/²  в единицах МэВ^-1. Результаты расчета этой величины для пяти возбужденных состояний ядра ¹⁷⁰Hf приведены в четвертой строке таблицы.
    Расчет показывает, что момент инерции ядра растет с увеличением момента количества движения и, соответственно, угловой частоты вращения. Этот результат хорошо понятен на основе капельной модели ядра: момент инерции капли растет с увеличением углового момента вращения.
    Важным и интересным фактом, который можно легко продемонстрировать на этом примере, является то, что полученные в расчете моменты инерции как минимум вдвое меньше, чем момент инерции твердотельного ротатора с такой же массой. Нижний предел величины , пропорциональной моменту инерции, можно получить по формуле момента инерции сферы радиуса R (здесь удобно использовать константу конверсии):

 = 2MR² / 5;

Таким образом, проведенный несложный расчет доказывает, что ядро в низших возбужденных состояниях имеет значения момента инерции, составляющие не более 50% момента инерции твердого ротатора с той же массой. Часть нуклонов ядра оказывается не участвующей во вращательном движении вследствие эффекта спаривания нуклонов, приводящего к сверхтекучим свойствам ядер в основном и низших возбужденных состояниях. Разрыв нуклонных пар, происходящий при очень высоких моментах вращения ядер, проявляется в скачкообразном росте момента инерции ядра до величин близких к полученной выше твердотельной оценке. Этот эффект (т.н. бекбендинг = backbending) хорошо изучен в последние 20 лет на ускорителях тяжелых ионов. Исследование спектров возбуждения ядер проводится, главным образом, путем измерения энергий гамма-квантов, испускаемых ядром при переходе с более высокого уровня на более низкий по энергии.

4. РАСПАДЫ И РЕАКЦИИ

4.1. Характеристики вероятностей распадов и реакций

Распады представляют собой спонтанное превращение любого объекта физики микромира (ядра или частицы) в несколько продуктов распада:

Реакция (в физике микромира) - это превращение двух взаимодействующих между собой объектов в два или более продуктов реакции:

Как распады, так и реакции подчиняются ряду законов сохранения, среди которых должны быть упомянуты, во-первых, следующие законы:

1. Закон сохранения энергии:     E = Сonst	(4.3)
2. Закон сохранения импульса:  P = Сonst	4(.4)
3. Закон сохранения момента количества движения  = Const	(4.5)
4. Закон сохранения электрического заряда Q = Сonst	(4.6)

    В дальнейшем будут обсуждаться и другие законы сохранения, действующие в распадах и реакциях. Перечисленные выше законы являются важнейшими и, что особенно существенно, выполняются во всех типах взаимодействий.
    Процессы взаимодействий объектов микромира, отражением которых являются распады и реакции, имеют вероятностные характерстики. Распады характеризуются вероятностями распада , либо обратной вероятности величиной среднего времени жизни  = (1/). Часто используется также связанная с этими характеристиками величина периода полураспада Т_1/2.
    Получим уравнение распада для частиц (или ядер). Убыль числа частиц (или ядер) за интервал времени пропорциональна  этому интервалу, числу частиц (ядер) в данный момент времени и вероятности распада:

Интегрирование (4.3) с учетом начальных условий дает :

Периодом полураспада называется время, за которое число частиц (или ядер) уменьшится вдвое: