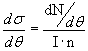4.5. Реакции с ядрами и частицами

При расчете кинематических характеристик реакций удобно использовать т.н. релятивистский инвариант E² - P²c² = m²c⁴ = inv, или E² - P² = m² в системе  = c = 1;   E - полная энергия системы, P - суммарный импульс.
    В качестве примера использования инварианта рассмотрим нахождение минимальной кинетической энергии сталкивающихся частиц в эндотермической реакции

(В эндотермической реакции сумма масс покоя частиц m_f,, образующихся в конечном состоянии, больше суммы масс покоя первичных частиц m_i.) В системе покоя мишени (частицы В) минимальная кинетическая энергия Т_А, при которой возможна реакция (4.21), называется порогом реакции. Для расчета порога реакции Т_А следует записать законы сохранения энергии и импульса в двух системах отсчета – лабораторной системе, связанной с покоящейся частицей В , и в системе центра масс, или центра инерции):

Порог реакции соответствует значению кинетической энергии частицы А в случае, когда кинетические энергии продуктов реакции минимальны. В системе центра масс в этом случае равны нулю кинетические энергии всех образовавшихся в результате реакции частиц. Одновременно равны нулю импульсы этих частиц. (Приравнять нулю импульсы и кинетические энергии продуктов реакции возможно только в системе центра инерции, в которой суммарный импульс по определению равен нулю). Найдем теперь значения E² - P²c² = inv для левой части уравнения (4.22) (т.е. в лабораторной системе координат) и правой части уравнения (4.23) (т.е. в системе центра масс) и приравняем их, используя таким образом свойство инвариантности:

    Из (4.24) получим

где  m_i = M_A + M_B.
Иногда вместо формулы (4.25) используется эквивалентное ей выражение

где

- энергия реакции

Приведем некоторые примеры использования формулы (4.25) для порогов реакции.

Формула расчета порога для данной реакции имеет вид:

Расчет числового значения пороговой энергии требует использования таблиц масс. Поскольку в справочных изданиях приводятся не массы ядер M_N, а массы атомов M или – альтернативно – избытки масс атомов D =M-A, формулу для пороговой реакции следует преобразовать, используя связь масс нейтральных атомов и масс ядер:

Используя таблицу избытков масс в единицах МэВ, приведенную в [1], получим для пороговой энергии фотона в реакции фоторасщепления ¹²С

(12 + 11 + 1)(8.668 МэВ + 7.289 МэВ) = 15.96 МэВ

Важно подчеркнуть, что расчет порога реакции с точностью до четырех знаков в данной задаче требует использования точных значений масс атомов только для разностей масс атомов.

Реакции рождения π⁰-мезона на электронном и протонном ускорителях имеют следующий вид:

Пороговые энергии электронов и протонов в реакциях (4.26) будут соответственно

T_e = m_π(2m_p + 2m_e + m_π)/2m_p
T_p = m_π(4m_p + m_π)/2m_p

Пользуясь таблицами масс в приложении к сборнику задач [1], получим для пороговых кинетических энергий электрона и протона в реакциях (4.26):

T_e = 135 МэВ (2·938 МэВ + 1 МэВ + 135 МэВ) / (2·938 МэВ)145 МэВ,
T_p = 135 МэВ (4·938 МэВ + 135 МэВ) / (2·938 МэВ)280 МэВ.

Столь значительное различие в пороговых энергиях при рождении пиона в реакциях электронов и протонов с неподвижной водородной мишенью является следствием больших затрат энергии на движение центра масс системы во второй реакции. Эти затраты отсутствуют в ускорителях на встречных пучках – коллайдерах (colliders). Именно коллайдеры являются основным инструментом современной физики высоких энергий в получении информации о структуре и свойствах частиц и их взаимодействий.

    Определим энергию  частицы в ускорителе с неподвижной мишенью, эквивалентном коллайдеру с энергиями E одинаковых частиц в пучках.
    В ускорителе со встречными пучками одинаковых по массе частиц лабораторная система совпадает с системой центра масс. В этой системе E² - P² = inv = 4E². В системе координат, связанной с одной из сталкивающихся частиц (например, частицей 2) энергия частицы 1 есть искомая энергия . В этой системе квадрат полной энергии равен (m + m + )², а квадрат полного импульса системы равен квадрату импульса частицы 1:  P² = (p₁)² = ² - m². Приравнивая значения инвариантов в этих двух системах, получим для энергии частицы в ускорителе с неподвижной мишенью, эквивалентном коллайдеру

Расчет энергий пучков в ускорителях с неподвижной мишенью, эквивалентных коллайдеру по (4.27), дает соответственно для энергий антипротонов

и для энергий позитронов

Относительно больший «выигрыш» в энергии для коллайдеров с электронными и позитронными пучками является следствием  зависимости энергии «эквивалентного» ускорителя с неподвижной мишенью (см. (4.27)) от массы ускоряемых частиц.

Полная энергия сталкивающихся протона и электрона составляет 930 Гэв в лабораторной системе координат. В этой же системе суммарный импульс равен разности импульсов протона и электрона. Обе частицы являются при указанных энергиях релятивистскими, поэтому их суммарный импульс равен 870 ГэВ. В системе неподвижной протонной мишени суммарная энергия равна M_p + , а импульс системы равен импульсу электрона Р₁ . Поскольку масса покоя электрона на насколько порядков меньше его энергии, Р₁ = . Приравнивая значение релятивистского инварианта в лабораторной системе координат и в системе, связанной с протоном, получим для  энергии электрона в системе неподвижного протона соотношение

E² - P² = (900 + 30)² - (900 - 30)² = ( + M_p)² - (² - M_p²) = 2М_p+M_p²

отсюда

    58·10³ ГэВ = 58 ТэВ

Реакция рождения "странных частиц": p + p → p + K⁺ + Σ⁰.

В ускорителе с неподвижной мишенью

В условиях коллайдера кинетические энергии обоих протонов идут – в предельном случае- на  создание масс продуктов. Поэтому минимальная (пороговая) энергия протона в коллайдере равна половине разности масс продуктов реакции и первичных частиц, что в данном случае составляет  всего  около 375 МэВ.

    Обсуждавшиеся выше задачи касались   законов сохранения энергии  и импульса в реакциях.
    Рассмотрим, как проявляются в реакциях другие законы сохранения -  например, закон сохранения момента импульса и закон сохранения пространственной четности  Р. (Напомним, что в реакциях, протекающих по сильному и электромагнитному взаимодействиям, четность Р сохраняется).

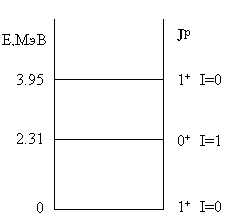
Реакция срыва

Закон сохранения момента импульса для данной реакции имеет вид:

Закон сохранения  Р- четности: (+1)(-1)=(+1)(+1)(-1)^ld, поэтому l_d - нечетное.
Единственным решением, удовлетворяющим  обоим законам сохранения является  l_d=1.
    В реакциях сильного взаимодействия выполняется также закон сохранения изоспина. Использование этого закона при анализе ядерных реакций является одним из способов идентификации  значения  изоспина.

Анализ закона сохранения изоспина для реакций сильного взаимодействия

приводит к выводу, что уровень с изоспином 1 в этих реакциях не может быть возбужден:   0 + 0 = 0 + I, I = 0.
    Для реакции неупругого рассеяния протонов
      
возможно возбуждение как состояний с изоспином 0, так и состояний с изоспином 1:
    0 +  = + ;  I = 0,1.

4.6. Эффективные сечения реакций

Характеристиками вероятности реакций являются дифференциальное и полное эффективные сечения реакции.
    Дифференциальное эффективное сечение реакции в системе покоя мишени (объекта Y в (4.2)) определяется как

Здесь θ - угол рассеяния, dN/dθ - число частиц, вылетевших под этим углом в единицу времени ( в секунду) в единичном телесном угле. I - величина потока частиц X, падающих на мишень. n - полное число частиц Y в мишени.
    Поскольку размерность числа частиц, рассеянных в единицу времени и в единицу телесного угла [s^-1sterad^-1], размерность потока [ I ] = [сm^-2s^-1] , а число частиц в мишени - безразмерная величина, получаем для размерности дифференциального сечения

Полное (или интегральное) эффективное сечение реакции имеет размерность см² и является интегралом от (4.29) по углу рассеяния

Поскольку эффективные сечения процессов микромира в единицах см² представляют собой очень малые величины, они измеряются, как правило, в следующих единицах 1барн = 1b = 10^-24 см².

Быстрыми нейтронами считаются нейтроны, длины волн которых много меньше размеров ядер. Проведем оценку кинетических энергий таких нейтронов

    _n = c / (T²+2T·m_nc²)^1/2 < Rr₀A^1/3

Для тяжелых ядер

    R10 Фм,         (T²+2T·940 МэВ)^1/2 > 200 МэВ·Фм / 10 Фм 20 МэВ

Отсюда кинетические энергии быстрых нейтронов приблизительно T >10 МэВ
    Исследование взаимодействия быстрых нейтронов с ядрами показало, что в сечение поглощения для нейтронов с длинами волн, много меньшими размеров ядра, близко к геометрическим размерам площади поперечного сечения ядра, т.е.R². Следует заметить, что этой же величине равно сечение упругого рассеяния нейтронов на ядре. Следовательно, полное сечение

Сечение поглощения быстрых нейтронов ядрами свинца

σ_abs =πR²3.14 (1.3)²(208)^2/3 Фм²2·10^-24 см² = 2 барн

Получение радиоактивных изотопов для медицинских и технических целей производится путем облучения нейтронам стабильных изотопов. Источником нейтронов является, например, ядерный реактор. Рассмотрим получение радиоактивного изотопа на примере  реакции активации золота

Полученный изотоп золота с А=198 – радиоактивный. Он распадается с  периодом полураспада Т_1/2=2.7 суток.

Рассмотрим  изменение числа ядер золота - 198 со временем, начиная от момента начала облучения золота - 197:

Здесь I – поток нейтронов,   n – число ядер золота 197 в образце,  σ – эффективное сечение реакции активации.

Активностью называется число распадов данного препарата в   1 сек. Активность равна вероятности распада на число ядер радиоактивного изотопа в образце
J(t) = λN(t) = In(1-e^-λt)

При условии, что время облучения  t << T_1/2 ,
λt = t·ln2/T_1/2<<1;  (1-e^-λt)1 - 1 + λt

Учитывая, что n = m·N_a/A, где m – масса активируемого образца,  N_A – число Авогадро, получаем, что наведенная активность изотопа  золота - 198 составляет