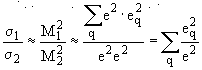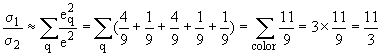6. Сильные взаимодействия

6.1. Квантовые числа адронов

Изоспин -

квантовый вектор, являющися характеристикой адронов.( Впервые введен для протонов и нейтронов - обоим нуклонам приписан одинаковый изоспин 1/2 - вектор в пространстве изоспина). Этот вектор может иметь два значения проекции на выделенную ось в изоспиновом пространстве: +1/2 - протон, и -1/2 - нейтрон. Введение этой характеристики инициировано важным свойством сильных взаимодействий - их независимостью от проекций изоспина. (Более точная формулировка этого положения: сильные взаимодействия инвариантны относительно вращений в пространстве изоспина). Например, замена протонов на нейтроны (и обратная операция) не изменяет эффективного сечения реакций сильного взаимодействия.
    Квантовая механика изоспина построена по аналогии с квантовой механикой момента количества движения, точнее - собственных моментов количества движения - спинов - в обычном пространстве.
    Величина изоспина адрона указывает на то, сколько у данного адрона состояний с различными проекциями изоспина. С точки зрения сильных взаимодействий протон и нейтрон являются двумя разными состояниями нуклона с изоспином 1/2 и двумя разными проекциями (изоспиновый дублет).
    Наиболее легкие из мезонов - пи-мезоны- существуют в трех зарядовых состояниях π^-,π⁰ и π⁺. Изоспин π-мезонов равен 1. Значения проекции изоспина -1, 0, +1 соответствуют трем зарядовым состояниям π-мезонов (изоспиновый триплет). Если частица не имеет “изоспинового партнера”, ее изоспин 0. Такой частицей является, например, Λ-гиперон. Σ-гиперон существует в трех зарядовых состояниях, его изоспин поэтому 1, а число проекций единицы равно 3 (1,0,+1), как и в случае π-мезонов.
    Изоспины адронов являются результатом сложения изоспинов составляющих их кварков. Квантовым числом изоспин обладают только кварки первого поколения, u и d, проекции их изоспинов, соответственно, +1/2 и -1/2. Изоспин антикварков также равен 1/2 (точно так же, как и спин), но проекции изоспинов меняют знак при переходе от кварков к антикваркам.

Гиперзаряд адронов

    Проекция изоспина адрона I_z, его заряд Q и другие квантовые числа связаны правилом Накано - Нишиджимы - Гелл-Манна.:

где Y = B + S - гиперзаряд (В-барионный заряд, S - странность). При исследовании адронов, в состав которых входят “тяжелые” кварки, выяснлось, что формула (6.1) верна и в этом случае, если ввести обобщенный гиперзаряд Y = B + S + c + b + t.
    Перечисленные в разделе 5 законы сохранения для всех реакций сильного взаимодействия выполняются без исключений. ( Это одновременно означает наибольшую, по сравнению с другими взаимодействиями, степень симметрий этих взаимодействий).

Спин адронов

является результатом векторного сложения спинов всех составляющих адронов кварков + орбитального момента кварков относительно центра масс частицы. Низшие по массе адроны составлены из кварков с нулевым орбитальным моментом.

Чем выше орбитальный момент кварков в адроне, тем выше масса адрона. На ускорителях высоких энергий обнаружены уже более сотни адронов - барионов и мезонов. (См. Таблицы частиц, а. также И.М. Капитонов. Введение в физику ядра и частиц. М.УРСС, 2002, стр.373, 374), где даны таблицы характеристик некоторых, главным образом низших по массе барионов и мезонов.

Четность адронов

представляет собой произведение четностей составляющих кварков и четности орбитального движения в кварковой системе:

6.2. Реакции сильных взаимодействий и законы сохранения

    Анализ законов сохранения позволяет идентифицировать неизвестную частицу, если ее рождение происходит в реакции сильного взаимодействия (см. раздел 5.2). Рассмотрим еще одну задачу, обратив главное внимание на изоспин частиц.

В реакциях сильного взаимодействия выполняются все законы сохранения. Определим характеристики частицы X:
Из закона сохранения заряда Q:
Q: +1+1 = +1+ Q(X) + 1 .Отсюда Q(X) = 0.
Закон сохранения барионного заряда:
B: +1+1 = +1 + B(X) + 0, т.е. B(X) = +1.
Закон сохранения странности:
S: 0 + 0 = S(X) + 1, т.е. S(X) = -1.

    Искомая частица - незаряженный барион с отрицательной странностью. Из таблицы частиц следует, что этому условию удовлетворяют две частицы Λ, Σ⁰. Кварковая структура обеих частиц (uds). Спин обеих частиц 1/2, барионный заряд равен 1. Отличие их структуры - в разных изоспинах.
   гиперон имеет изоспин 0, а нейтральный Σ⁰ гиперон принадлежит к группе трех Σ гиперонов с изоспином 1. Проекции изоспина у членов этой тройки ( изоспинового триплета) составляют -1, 0 и +1. Нейтральный Σ⁰ гиперон - центральный член триплета с проекцией изоспина 0.
    Проведем анализ закона сохранения изоспина в сильных взаимодействиях для реакции (6.4). Изоспин протона 1/2, суммирование двух векторов дает либо 0, либо 1. Это возможные значения изоспина двух протонов в начальном состоянии. В конечном состоянии три частицы. Изоспин К -мезонов также равен 1/2. Поэтому сумма изоспинов протона и К-мезона - также либо 0, либо 1. Отсюда получаем, что изоспин неизвестной частицы может принимать следующие значения 0, 1, 2. Поэтому полученный выше результат - либо Λ, либо Σ⁰ гиперон - соответствует возможным значениям изоспина.

     Δ⁺⁺ резонанс - частица, имеющая спин 3/2 и изоспин 3/2. Рассмотрим закон сохранения изоспина в этой реакции сильного взаимодействия

= Const; + = (,).

Таким образом, во взаимодействии пионов и нуклонов могут появиться частицы (резонансы) как и изоспином 1/2, так и с изоспином 3/2.

6.3. Адронные мультиплеты. Цвета кварков и глюонов

Симметрии в кварковой структуре адронов

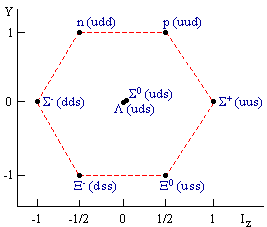
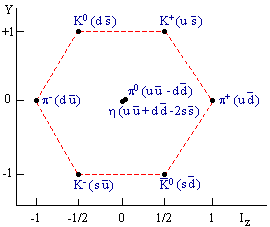
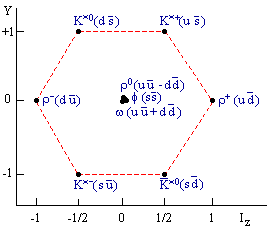
    Предположение о составной природе адронов было высказано еще в середине 60-х годов, после обнаружения т.н.”странных” частиц, главной особенностью которых было их ассоциативное рождение. Ассоциативное рождение частиц с квантовыми числами s, c, b, t - следствие соответствующих законов сохранения ( см. таблицу 5.2). Например, в реакции задачи 5.1 появляются две такие частицы с противоположной странностью. Симметрия в структуре адронов очевидным образом проявляется в адронных октетах. На схемах показаны три таких октета. Первый - октет наиболее легких барионов, второй и третий - мезонные октеты. По оси ординат в этих схемах отложена сумма странности и барионного заряда, по оси абсцисс - проекция изоспина частиц. Первый - барионный - октет содержит частицы со спином 1/2. Второй (мезонный) октет - частицы со спином 0. Третий (мезонный) октет - частицы со спином 1. Изучение этих октетов привело к гипотезе о кварковой структуре всех частиц этих октетов (и далее к выводу о кварковой структуре всех адронов).

    Первая строка октета барионов содержит частицы, состоящие из кварков первого поколения u и d - это протон и нейтрон. Сумма странности и барионного заряда для них равна 1. Вторая строка этого октета содержит барионы, в состав которых входит один странный s кварк. Сумма странности и барионного заряда для этой строки равна 0. В третьей строке - частицы с двумя странными s -кварками. Их всего две. Изоспин этих Ξ-гиперонов равен 1/2, сумма барионного заряда и странности равна -1. Схема сложения спинов кварков этих барионов =1/2. Второй октет (мезонный) соответствует сложению спинов кварка и антикварка в ноль: = 0. (Это псевдоскалярные мезоны). Третий октет, при той же кварковой структуре мезонов, соответствует схеме сложения спинов кварка и антикварка в 1: = 1. Это т.н. векторные мезоны. Векторные мезоны тяжелее псевдоскалярных, что указывает на зависимость сил, действующих между кварками, от ориентации спинов кварков. (Следует отметить, что в схеме векторных мезонов в центре находятся не две, как в октете барионов, а три частицы - т.е. схема векторных мезонов представляет собой сумму октета и синглета.)

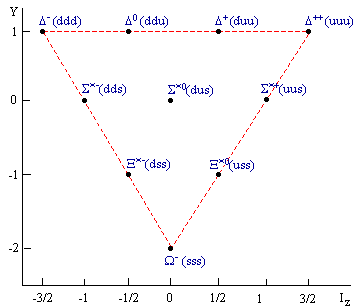
Спины трех кварков, составляющих барионы, могут быть и параллельными друг другу, составляя в сумме спин 3/2. Эти частицы также обнаружены экспериментально, на схеме, аналогичной предыдущим, они составляют декуплет -10 частиц.

Colour = цвет

    Частицы, расположенные по углам декуплета, составлены из одинаковых кварков (т.е. кварков с одинаковым квантовым числом  flavor = аромат). Проекции их спинов совпадают. Противоречие с принципом Паули?! Нет, противоречия нет потому, что кваркам присуще еще одно квантовое число, отсутствующее у непосредственно наблюдаемых частиц - т.н. “цвет” = colour. Три кварка в составе бариона имеют три разных квантовых числа цвет, причем сумма этих квантовых чисел дает отсутствие цвета - барионы “бесцветные” (иногда говорят- белые) То же относится и к мезонам, состоящим из суперпозиции трех кварк-антикварковых пар: красный-антикрасный + желтый-антижелтый + синий-антисиний.
    Цветные кварки в составе “бесцветных” адронов связаны путем обмена глюонами. Переносчики сильного взаимодействия -глюоны- имеют не один, а два цветовых индекса. Всего имеется не 9, а 8 цветных глюонов, поскольку комбинация жж + сс + кк не имеет цветового заряда (т.е. является "белой"). Свободные кварки и глюоны не существуют: они "заперты" внутри бесцветных адронов (confinement).

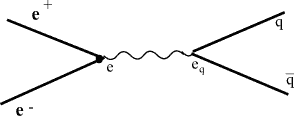
Рассмотрим закон сохранения изоспина I и его проекции I₃ :

  = Const; + = (0,) = + .
I₃ : +1/2-1/2 = 0 ;

Законы сохранения момента импульса и четности:
J:  + + _p = 0 + 0 + _{π π} = l_p,   l_p + 1

P: 
Отсюда следует, что орбитальные моменты протонной и пионной пар должны совпадать.

Задача 6.4. Оценить отношение эффективных сечений двух электромагнитных процессов в коллайдере : 1) реакции аннигиляции пары e+, e- с появлением двух “струй” адронов ; 2) реакции аннигиляции пары e+, e- с рождением пары пары +, -. Экспериментальное исследование этого отношения проведено на электрон-позитронном коллайдере PETRA.

    На схемах показаны диаграммы Фейнмана для реакции 1 и 2. В реакции 1 рождается пара кварк-антикварк. Поскольку “цветные” силы взаимодействия между кварками резко возрастают при увеличении расстояния между ними, разлет кварков сопровождается рождением из вакуума еще нескольких пар кварк-антикварк - т.н. “морских” кварков. Первичные кварки “одеваются” этими парами, образуя струи бесцветных адронов, движущихся в направлении вылета первичных кварков. Так образуются регистрируемые экспериментально адронные струи (jets) .

1) 2) Рис.6.5. Диаграммы Фейнмана реакций аннигиляции пары e+, e-

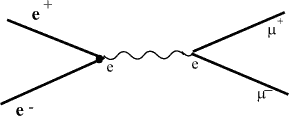
Во втором процессе рождаются мюонные пары. ( Здесь обсуждаются только два из возможных процессов аннигиляции пар e⁺, e^-) . Пунктирной линией на рис.6.5 обозначены γ-кванты. Как обсуждалось в Разделе 5, сечение процесса пропорционально квадрату его матричного элемента σ ~ M². Матричный элемент процесса 2 пропорционален квадрату константы взаимодействия, которая в “естественной” системе равна заряду α_e^1/2 = e^1/2/(c) → e. Эти константы характеризуют все вершины процесса 2 и правую вершину процесса 1. В левой вершине процесса 1 стоит в качестве константы взаимодействия должен стоять заряд кварка e_q. Отсюда отношение сечений исследуемых процессов есть

Результат суммирования зависит от числа кварков, которые могут рождаться в реакции1. При энергиях электрон-позитронного коллайдера PETRA возможно появление всех кварков таблицы 5.1, за исключением самого массивного t кварка. Тогда формула (6.5) имеет следующий вид:

Это отношение сечений процессов 1 и 2 - результат учета 3 цветов для кварков каждого из ароматов (flavor). Именно такое отношение и получено в результате эксперимента на коллайдера PETRA. Этот результат является прямым подтверждением существования квантового числа цвет.

Задание 4 (к разделам 5 и 6)

1. Доказать невозможность поглощения -кванта любой свободной частицей.
2. Построить диаграммы Фейнмана для процессов рассеяния гамма- кванта на свободном электроне и для процесса аннигиляции пары электрон-позитрон
3. Почему при аннигиляции электрона и позитрона не может возникнуть менее, чем два -кванта?
4. Определить минимальную кинетическую энергию протонов (пороговую энергию ) в реакции рождения нейтрального пиона p + p → p + p + π⁰.
5. Определить пороговое значение энергии протона в реакции p + p → p + Σ⁺ + K⁰. Проверить выполнение законов сохранения.
6. Идентифицировать частицу Х в реакции сильного взаимодействия π^- + p → Ω + X + K⁰ + K⁰.
7. Составить таблицу возможных квантовых чисел системы пион-нуклон.
8. Проверить выполнение законов сохранения и построить кварковые диаграммы реакций сильного взаимодействия:
   K^- + p → Σ^- + π⁺;
   π^- + p → Λ + K⁰;
   π^- + p → π⁰ + n.
9. Идентифицировать частицу Х в реакции сильного взаимодействия K^- + p → X + K⁺ + K⁰. Построить кварковую диаграмму реакции.
10. Определить среднее время жизни ⁺⁺ резонанса. Написать реакцию, в сечении которой наблюдается этот резонанс.
11. Построить таблицу квантовых чисел антипротона.
12. Рассчитать энергию столкновения электрона и позитрона на коллайдере LEP. Энергии пучков равны по 100 ГэВ.
13. Найти орбитальный момент пиона в реакции сильного взаимодействия: π^- + p → Δ⁰ → π^- + p.
14. Проанализировать выполнение принципа Паули для кварков, составляющих барионы, входящие в барионный декуплет. Показать необходимость введения нового квантового числа "цвет".