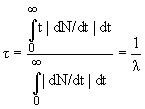 . . |
(3) |
Способность ядер самопроизвольно распадаться, испуская
частицы, называется радиоактивностью. Радиоактивный распад -
статистический процесс. Каждое радиоактивное ядро может распасться в любой
момент и закономерность наблюдается только в среднем, в случае распада
достаточно большого количества ядер.
Постоянная распада λ - вероятность
распада ядра в единицу времени.
Если в образце в момент времени t имеется N
радиоактивных ядер, то количество ядер dN, распавшихся за время dt
пропорционально N.
| dN = -λNdt. | (1) |
Проинтегрировав (1) получим закон радиоактивного распада
| N(t) = N0e-λt. | (2) |
N0 - количество радиоактивных ядер в момент времени t = 0.
Cреднее время жизни τ -
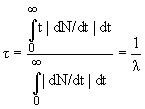 . . |
(3) |
Период полураспада T1/2 - время, за которое первоначальное количество радиоактивных ядер уменьшится в два раза
| T1/2 = ln2/λ=0.693/λ = τln2. | (4) |
Активность A - среднее количество ядер распадающихся в единицу времени
| A(t) = λN(t). | (5) |
Активность измеряется в кюри (Ки) и беккерелях (Бк)
1 Ки = 3.7·1010 распадов/c,
1 Бк = 1 распад/c.
Распад исходного ядра 1 в ядро 2, с последующим его распадом в ядро 3, описывается системой дифференциальных уравнений
| dN1/dt = -λ1N1 dN2/dt = -λ2N2 +λ1N1, |
(6) |
где N1(t) и N2(t) -количество ядер, а λ1 иλ2 - постоянные распада ядер 1 и 2 соответственно. Решением системы (6) с начальными условиями N1(0) = N10; N2(0) = 0 будет
|
|
(7a) |
| (7б) |
Количество ядер 2 достигает максимального значения ![]() при
при ![]() .
.
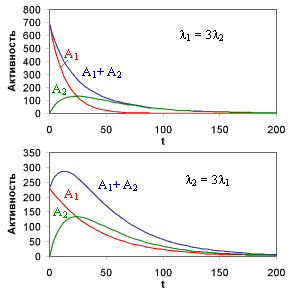 Если λ2
< λ1
(
Если λ2
< λ1
(![]() >
>![]() ), суммарная активность
), суммарная активность
Если λ2 >λ1 (![]() <
<![]() ), суммарная
активность вначале растет за счет накопления ядер 2.
), суммарная
активность вначале растет за счет накопления ядер 2.
Если λ2 >>λ1, при достаточно больших временах вклад
второй экспоненты в (7б) становится пренебрежимо мал, по сравнению со вкладом
первой и активности второго A2 = λ2N2 и
первого изотопов A1 = λ1N1
практически сравняются. В дальнейшем активности как первого так и второго
изотопов будут изменяться во времени одинаково.
| A1(t) = N10λ1 |
(8) |
То есть устанавливается так называемое вековое равновесие, при котором число ядер изотопов в цепочке распадов связано с постоянными распада (периодами полураспада) простым соотношением.
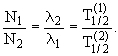 |
(9) |
Поэтому в естественном состоянии все изотопы, генетически связанные в
радиоактивных рядах, обычно находятся в определенных количественных
соотношениях, зависящих от их периодов полураспада.
В общем случае, когда имеется цепочка распадов 1→2→...n,
процесс описывается системой дифференциальных уравнений
| dNi/dt = -λiNi +λi-1Ni-1. | (10) |
Решением системы (10) для активностей с начальными условиями N1(0) = N10; Ni(0) = 0 будет
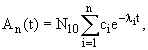 |
(11) |
где
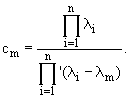 |
(12) |
Штрих означает, что в произведении, которое находится в знаменателе, опускается множитель с i = m.
11.05.2017