Корпускулярные и волновые свойства частиц. Принцип неопределенности

    В 1900 г. была опубликована работа М. Планка, посвященная проблеме теплового излучения тел. М. Планк моделировал вещество как совокупность гармонических осцилляторов различной частоты. Предположив, что излучение происходит не непрерывно, а порциями - квантами, он получил формулу для распределения энергии по спектру теплового излучения, которая хорошо согласовывалась с опытными данными

,

где h - постоянная Планка, k - постоянная Больцмана, T - температура, ν - частота излучения.

    Так, впервые в физике появилась новая фундаментальная константа - постоянная Планка. Гипотеза Планка о квантовой природе теплового излучения противоречит основам классической физики и показала границы ее применимости.
    Через пять лет А. Эйнштейн, обобщив идею М. Планка, показал, что квантованность является общим свойством электромагнитного излучения. Согласно Эйнштейну электромагнитное излучение состоит из квантов, названных позднее фотонами. Каждый фотон имеет определенную энергию и импульс:

E = hν,  = (h/λ),

где λ и ν - длина волны и частота фотона, - единичный вектор в направлении распространения волны.

    Представления о квантованности электромагнитного излучения позволили объяснить закономерности фотоэффекта, исследованные экспериментально Г. Герцем и А. Столетовым. На основе квантовой теории А. Комптоном в 1922 году было объяснено явление упругого рассеяния электромагнитного излучения на свободных электронах, сопровождающееся увеличением длины волны света. Открытие двойственной природы электромагнитного излучения - корпускулярно-волнового дуализма оказало значительное влияние на развитие квантовой физики, объяснение природы материи.

Зависимость длины волны от энергии для различных частиц

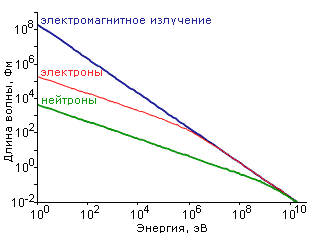
    В 1924 г. Луи де Бройль выдвинул гипотезу об универсальности корпускулярно-волнового дуализма. Согласно этой гипотезе не только фотоны, но и любые другие частицы материи наряду с корпускулярными обладают также и волновыми свойствами. Соотношения, связывающие корпускулярные и волновые свойства частиц, те же, что были установлены ранее для фотонов

E = h = ω, = , |p| = h/λ/,

где h = 2π, ω = 2πν, = 2π - длина волны (де Бройля), которую можно сопоставить с частицей. Волновой вектор ориентирован по направлению движения частицы. Прямыми опытами, подтверждающими идею корпускулярно-волнового дуализма частиц, были опыты, выполненные в 1927 году К. Дэвиссоном и Л. Джермером по дифракции электронов на монокристалле никеля. Позднее наблюдалась дифракция и других микрочастиц. Метод дифракции частиц в настоящее время широко используется в изучении строения и свойств вещества.
    Экспериментальное подтверждение идеи корпускулярно-волнового дуализма привело к пересмотру привычных представлений о движении частиц и способа описания частиц. Для классических материальных точек характерно движение по определенным траекториям, так, что их координаты и импульсы в любой момент времени точно известны. Для квантовых частиц это утверждение неприемлемо, так как для квантовой частицы импульс частицы связан с ее длиной волны, а говорить о длине волны в данной точке пространства бессмысленно. Поэтому для квантовой частицы нельзя одновременно точно определить значения ее координат и импульса. Если частица занимает точно определенное положение в пространстве, то ее импульс полностью неопределен и наоборот, частица с определенным импульсом имеет полностью неопределенную координату. Неопределенность в значении координаты частицы Δx и неопределенность в значении компоненты импульса частицы Δp_x связаны соотношением неопределенности, установленным В. Гейзенбергом в 1927 году

Δx·Δp_x.

     Из принципа неопределенности следует, что в области квантовых явлений неправомерна постановка некоторых вопросов, вполне естественных для классической физики. Так, например, не имеет смысла говорить о движении частицы по определенной траектории. Необходим принципиально новый подход к описанию физических систем. Не все физические величины, характеризующие систему, могут быть измерены одновременно. В частности, если время жизни некоторого состояния равно Δt, то неопределенность величины энергии этого состояния ΔE не может быть меньше ΔE/, т.е.

ΔE·Δt.

Задачи