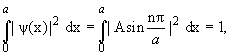Волновая функция

    Наличие у частицы волновых свойств приводит к тому, что в квантовой физике ей сопоставляется волновая функция (x,y,z,t).
    Физический смысл волновой функции. Величина |(x,y,z,t)|²dV пропорциональна вероятности того, что частица будет обнаружена в момент времени t в объеме dV в окрестности точки (x,y,z).
    Волновая функция системы невзаимодействующих частиц (r₁,r₂,...r_n,t) связана с одночастичными волновыми функциями _i(r_i,t) соотношением

(r₁,r₂,...r_n,t) = ₁(r₁,t)·₂(r₂,t)·..._n(r_n,t).

Свободное движение частицы

Волновая функция свободно движущейся частицы с энергией E и импульсом p имеет вид

(r,t) = Aexp[i(kr - t)] = Aexp[i(pr - Et)/] .

Константа A может быть найдена из условия нормировки волновой функции

A = (2)^-3/2.

Т.е. в тех случаях, когда частица находится в области пространства, где действующие на нее силы равны нулю (свободное движение), энергия частицы может принимать любые значения. Энергетический спектр свободно движущейся частицы непрерывный.

Частица в прямоугольной яме с бесконечными стенками

Если область пространства, в которой может находится частица ограничена, возникает дискретный спектр энергий. Рассмотрим это на примере одномерной прямоугольной ямы c бесконечными стенками

Частица всегда находится в области 0 < x < a. Вне ее = 0. Запишем уравнение Шредингера для одномерного случая

(1)

Его решение

= Asin kx + Bcos kx,

(2)

где k = (2mE/²)^1/2. Из граничных условий и условий непрерывности имеем

Asin ka = 0.

(3)

Из (3) получим

ka = n, n = 1, 2, ...,

(4)

т.е. внутри ямы устанавливаются стоячие волны, а энергия состояний принимает дискретные значения

E_n = p²/2m = k²/2m = ²²n²/(2ma²).

(5)

Энергии состояний растут квадратично от n.

Рис. 1

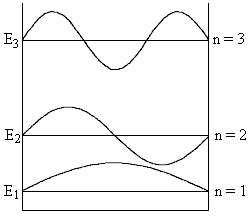
Каждому значению энергии соответствует волновая функция, которую с учетом условия нормировки

(6)

можно записать в виде

_n = (2/a)^1/2sin (nx/a)

(7)

(см. рис.1). В отличие от классической частицы, квантовая частица в прямоугольной яме не может иметь энергию E < ²²/(2ma²).

Частица в потенциале гармонического осциллятора

Потенциал гармонического осциллятора (так же, как и в предыдушем примере рассмотрим одномерный случай)

_n = kx²/2 = m₀x²/2.

(8)

где ₀= (k/m)^1/2 - собственная частота колебаний гармоничекого осциллятора. Решение уравнения Шредингера для этого потенциала можно записать в виде

_n = h_n(x)e^-b(x),

(9)

где h_n(x) - полиномы степени n, b(x) = (km)^1/2x²/2. Спектр значений энергий имеет вид

E_n = ₀(n + 1/2), n = 0, 1, ...

(10)

Энергетический спектр гармонического осциллятора эквидистантный - уровни находятся на одинаковом расстоянии друг от друга.

24.12.12