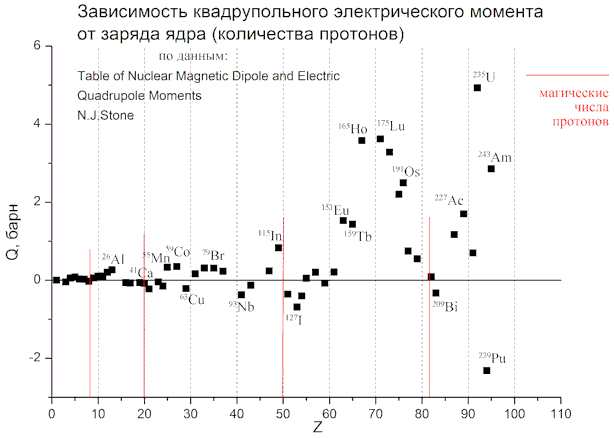
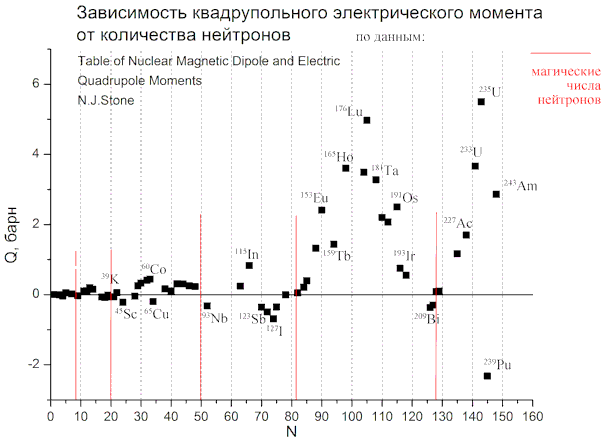
Зависимость электрического квадрупольного момента от числа нуклонов в ядре

    Электрический квадрупольный момент (Q) – характеристика атомного ядра, проявляющаяся в его взаимодействии с внешним электрическим полем. Измеряемый квадрупольный момент (его проекция на направление поля) служит мерой несферичности ядра:

Q₀ = ∫ ρ(r)(3z² – r²)dV = Ze ∫ |Ψ|²(3z² – x² – y² – z²)dV = Ze (2<z²> – <x²> – <y²>),

если в этом выражении средний квадрат радиуса по оси z больше, чем по x и y, то ядро "вытянутое" и Q₀ положительный. Если средний квадрат радиуса по z меньше, чем по x и y, то ядро "сплюснутое" и Q₀ отрицательный.

    Оператор квадрупольного момента

    Электрические операторы с разной мультипольностью λ определяются следующим образом:

    Оператор квадрупольного момента определяется:

    Измеряемое значение квадрупольного момента (максимальное) определяется как диагональный матричный элемент оператора с проекцией полного момента J, равной самому этому моменту, то есть:

Здесь N – главное квантовое число радиальной части волновой функции, и матричный элемент угловой части оператора имеет следующий вид:

<J, M = J|Y_2m|J, M = J> – то, что зависит только от θ и φ в выражении .

    Для его анализа используем теорему Вигнера-Эккарта:

Поэтому матричные элементы зависят от проекций моментов только через коэффициенты Клебша-Гордона. В нашем случае получаем:

    Этот матричный элемент не равен нулю, если <JJ|2mJJ> не равен нулю, что выполняется при m = 0 и J больше или равен единице. Таким образом, измеряемый квадрупольный момент ядра равен нулю, если полный момент ядра меньше единицы. Так, он равен нулю для всех четно-четных ядер, хотя многие из них являются несферическими и имеют внутренний (собственный) квадрупольный момент, отличный от нуля.
    На данных графиках представлена зависимость величины электрического квадрупольного момента от числа нуклонов в ядре – отдельно для протонов и нейтронов. Можно видеть, что в этой зависимости присутствуют максимумы – примерно на середине расстояния между магическими числами протонов или нейтронов, а в самих значениях магических чисел (отмечены красными вертикальными линиями) квадрупольный момент близок к нулю. Это прослеживается на обоих графиках.
    Также видно, что ядер с положительным квадрупольным моментом больше, чем с отрицательным. Это говорит о том, что "вытянутых" ядер больше, чем "сплюснутых".
    Видно возрастание величины квадрупольного момента для ядер с зарядом в районе 70 и трансурановых элементов.

    Данные взяты из таблицы N.J. Stone, "Table of Nuclear Magnetic Dipole and Electric Quadrupole Moments". http://www.nndc.bnl.gov/publications/preprints/nuclear-moments.pdf

    Основные экспериментальные методы, которые были использованы для получения данных таблицы:

• Atomic Beam Magnetic Resonance
• Molecular Beam Magnetic Resonance
• Coulomb Interaction of Aligned Nuclei
• Atomic Beam Laser Spectroscopy
• Atomic Beam with Laser Double Resonance Detection
• Laser Resonance Fluorescence Spectroscopy
• Nuclear Magnetic Resonance on Oriented Nuclei
• Pionic X-ray Hyperfine Structure
• Collinear Fast Beam Laser Spectroscopy - Accelerated Beam
• Re-evaluated by tabulator, usually because of change in reference standard
• Optical Spectroscopy

Используемая литература:

1. N.J. Stone, "Table of Nuclear Magnetic Dipole and Electric Quadrupole Moments".

2. Н.Г. Гончарова. Введение в физику атомного ядра. 12 лекций.

18.12.2012