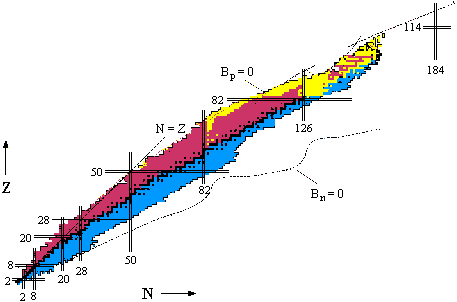
1. N-Z диаграмма атомных ядер
Атомные ядра представляют собой квантовые системы нуклонов,
связанных между собой ядерным взаимодействием. Свойства атомных ядер
определяются совместным действием сильных, электромагнитных и слабых
взаимодействий.
В настоящее время обнаружено ~ 3500 атомных ядер,
представляющих собой различные сочетания протонов (в количестве Z) и
нейтронов (в количестве N). По существующим оценкам число атомных ядер может
составлять ~ 6500.
На диаграмме с левой стороны от стабильных ядер находятся
ядра, перегруженные протонами (протоно-избыточные ядра), справа – ядра,
перегруженные нейтронами (нейтроно-избыточные ядра). 2. Радиоактивность
Радиоактивностью называется способность атомного ядра
самопроизвольно распадаться с испусканием частиц.
К более редким видам радиоактивного распада относятся
процессы испускания ядрами двух электронов, одного или двух протонов, а также
кластеров
– лёгких ядер от 12C до 32S. Во всех видах
радиоактивности (кроме γ-распада) изменяется состав ядра – число протонов Z,
массовое число Aили и то и другое одновременно. dN= -λNdt. Закон радиоактивного распада имеет вид: N(t) = N0e-λt, где N0 – количество радиоактивных ядер в исходный момент времени t = 0. Среднее время жизни τ:
Период полураспада T1/2 – время, за которое первоначальное количество радиоактивных ядер уменьшается в два раза: T1/2 = ln2/λ=0.693/λ = τln2. 3. Масса атомного ядраМасса атомного ядра – одна из важнейших его характеристик. Измерения масс атомных ядер показали, что масса ядра отличается от суммы масс свободных протонов и нейтронов, входящих в его состав. 3.1. Энергия связи ядраЭнергия связи Eсв ядра (A,Z) - выраженная в энергетических единицах разность между массой M(A,Z) ядра и суммой масс (A- Z) нейтронов и Zпротонов: Eсв(A,Z) = [(A - Z)Mn + ZMp) - M(A,Z)]c2.
Энергия связи ядра Eсв
определяет минимальную энергию, которую надо затратить, чтобы разделить ядро на
отдельные нуклоны.
Значения коэффициентов a1
- a5
были подобраны так, чтобы наилучшим образом воспроизвести экспериментальные
значения масс стабильных ядер:
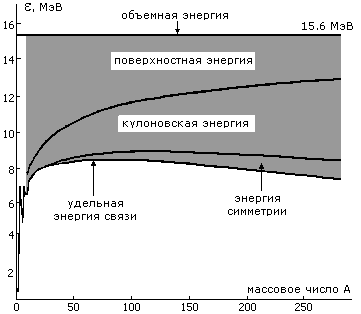
Энергия связи Eсв(A,Z) растет с ростом
массового числа A, достигая величины 3.2. Атомная единица массы В атомной и ядерной физике для выражения масс атомов и
атомных ядер используется специальная единица - атомная единица массы. 1 а.е.м (u) ≈ 1.66056×10-27 кг.
В ядерной физике вместо массы ядра М используют (в соответствии с соотношением
Эйнштейна
3.3. Избыток (дефект) массыРазность между массой атома в атомных единицах массы и массовым числом A называется избытком (дефектом) массы Δ(A,Z): Δ(A,Z) = М(A,Z) – A. 3.4. Измерение масс атомных ядерСуществует несколько методов измерения масс атомных ядер. 3.4.1. Масс спектрометрыОдним из широко используемых методов определения масс атомных ядер является анализ характеристик движения ионов в электрических и магнитных полях. Если магнитное поле индукции B направлено перпендикулярно траектории движения иона с массой Mиона и зарядом Zиона, то радиус кривизны r траектории движения иона зависит от его кинетической энергии T:
Из приведенного соотношения, зная радиус кривизны r
траектории движения иона в магнитном поле, можно определить массу иона Mиона. 3.4.2. Измерение масс атомных ядер методом времени пролёта и магнитного анализаОпределение массы ядра A~ 100 с точностью ~ 100 кэВ эквивалентно относительной точности измерения массы ~ 10-6. Для достижения такой точности используют совместное измерение времени пролета и магнитный анализ продуктов ядерной реакции. Магнитная жесткость спектрометра Br, масса ядра M, его скорость v и заряд qсвязаны соотношением Br =Mv/q. Зная магнитную жесткость спектрометра Br, можно определить отношение массы ядра к его заряду M/q. Этот метод позволяет определить массы ядер с точностью 10-4. Точность измерения масс ядер можно повысить, если одновременно измерять время пролета атомного ядра между двумя реперными точками (пролетная база). В этом случае масса иона определяется из соотношения:
где L– пролетная база, T– время пролета. 3.4.3. Определения масс ядер методом измерения циклотронной частотыДля ядра, движущегося в постоянном магнитном поле B, частота вращения ω связана с его массой M и зарядом qсоотношением: B/ω =M/q. Несмотря на то, что методы 3.4.2 и 3.4.3 основаны на одном и том же принципе, точность в методе измерения циклотронной частоты выше (~10-7), т.к. он эквивалентен использованию пролетной базы гораздо большей длины. 3.4.4. Измерение масс атомных ядер в накопительном кольцеМетод применим для определения масс ядер, имеющих время жизни > 1 мин. Метод измерения циклотронной частоты ионов в накопительном кольце применяется в комбинации с предварительной сепарацией ионов на лету. 3.4.5. Измерения масс ядер с помощью ловушки Пеннинга (Penning Trap)
Новые экспериментальные возможности для прецизионного
измерения масс атомных ядер открываются в комбинации методов сепарации ионных
пучков ISOL (Isotop Separation
On-Line) и ионных ловушек. Для ионов, имеющих небольшую
кинетическую энергию и, следовательно, малый радиус вращения в сильном магнитном
поле, используется ловушка Пеннинга. 3.4.6. Измерение энергии реакции QВ двухчастичных реакциях A + a → B + b массы ядер связаны соотношениемMA + Ma =MB + Mb + Q.
Если известны массы трех ядер, то масса четвертого ядра
вычисляется по результатам измерения энергии реакции Q.
3.4.7. Измерение энергии β-распада Qβ
Измерение энергии β-распада Qβ
является распространенным методом определения масс ядер, расположенных вдали от
долины стабильности.
A → B+ e-(e+) +
неизвестная масса MA ядра Aможет быть определена из соотношения MA = MB + me + Qβ,
где MB
– масса ядра B, me
– масса электрона, а Qβ
– измеренная энергия β-распада.
3.4.8. Измерение энергииα-распада QαДля α-радиоактивных ядер масса ядра определяется из данных по энергетическим спектрам α-частиц (энергиям α-частиц - Eα), образующихся в результате α-распада исходного ядра A A → B+ α. Массы исходного ядра MA, конечного ядра MB и α-частицыMα, образующейся в результате α-распада, связаны соотношением MA = MB + Mα + Qα,
где Qα
- энергия α-распада. Qα = Eα(MB + Mα)/MB. Если конечное ядро B образуется в возбужденном состоянии, необходимо учитывать его энергию возбуждения. Точность, с которой по энергии α-распада определяется масс атомного ядра, составляет ~ 50 кэВ. Этот метод широко используется для определения масс сверхтяжелых атомных ядер и их идентификации. |
|||||||||||||||||||||||||||||
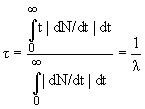 .
.