10. База данных основных состояний атомных ядер.
Калькулятор свойств ядер и характеристик ядерных процессов

    В Центре данных фотоядерных экспериментов НИИЯФ МГУ имеется постоянно обновляемая база данных (БД) [11] по параметрам основных и изомерных состояний атомных ядер (рис. 20). В ней содержится информация [12] обо всех ядрах, обнаруженных к последнему обновлению базы. БД содержит (см. рис. 21 и Раздел 11) следующие параметры атомного ядра:

• А – массовое число ядра;
• Z – число протонов в ядре;
• N - число нейтронов в ядре;
• T_1/2 - период полураспада радиоактивного ядра, Г – ширина распада радиоактивного ядра, распространенность стабильного ядра;
• J^P- спин J и чётность P основного или изомерного состояния ядра;
• масса атома M, а.е.м. - масса атома в атомных единицах массы;
• масса атома M, МэВ – масса атома в МэВ;
• избыток (дефект) массы Δ = M - А в кэВ;
• энергия связи - энергия связи ядра в кэВ;
• моды распада радиоактивного ядра.

    С использованием информации, представленной в БД по параметрам основных состояний ядер, может быть рассчитан ряд величин, характеризующих как свойства атомных ядер, так и процессы их превращений друг в друга в реакциях и распадах.

Рис. 20. Пример заполнения поисковой формы БД для нахождения параметров основных состояний ядер в диапазоне Z = 80 - 100.

Рис. 21. Выходная форма БД с параметрами основных состояний ядер с Z = 80 – 100.

    Для расчета различных параметров атомных ядер, энергетических характеристик ядерных реакций и радиоактивных распадов ядер была реализована специальная компьютерная программа - интерактивный калькулятор [http://cdfe.sinp.msu.ru/services/calc_thr/calc_thr_ru.html], состоящий из пяти поисковых форм:

«1. Энергии связи ядер» (рис. 22, 25);
«2. Энергии отделения нуклонов и ядер» (рис. 27, 29, 31);
«3. Энергии распадов» (рис. 33, 35);
«4. Пороги и энергии реакций» (рис. 37);
«5. Энергия деления» (рис. 39).

    В каждой поисковой форме присутствуют кнопки «Вычислить» и «Очистить»:

• при нажатии кнопки «Вычислить» (см. далее рис. 22 и др.) появляется таблица, содержащая запрашиваемую числовую информацию (используются данные, приведённые в таблице атомных ядер [11]);
• кнопка «Очистить» возвращает все поля формы в исходное состояние (состояние по умолчанию).

    В первых трех (1, 2, 3) поисковых формах присутствуют кнопки «Построить график» и панель “На оси абсцисс”, с помощью которых возможно воспроизвести в нужном виде графики зависимостей запрашиваемых величин от одного из выбранных чисел Z, N, A.
    В двух последних формах (4, 5) эти кнопка и панель отсутствуют, поскольку при расчетах порогов и энергий реакций, а также энергии деления диапазон параметров не предусмотрен.
    Ниже приведено несколько примеров того, какая информация о свойствах атомных ядер и характеристиках ядерных взаимодействий может быть получена из анализа масс атомных ядер.

Энергия связи ядра E_св(A,Z)

    Энергия связи ядра E_св(A,Z) может быть выражена через массу ядра M(A,Z), массу протона M_p и массу нейтрона M_n

E_св(A,Z) = [ZM_p + (A − Z)M_n − M(A,Z)]c²,

    Сравнение удельных энергий связи лёгких и тяжёлых ядер показывает энергетическую выгодность слияния легких ядер и деления тяжелых ядер. Эта информация даёт прекрасный иллюстративный материал при изучении вопросов деления тяжёлых ядер и ядерного нуклеосинтеза лёгких ядер. Более точные представления о величине энергии связи ядер можно получить, сравнивая различные сечения энергетической зависимости удельной энергии связи ядра ε(A,Z) = E_св(A,Z)/A от массового числа A, числа нейтронов N в различных изотопах (ядрах с одинаковым значением Z) или числа протонов Z в различных изотонах (ядрах с одинаковым значением N).
    Для нахождения энергии связи ядра разработана 1-я поисковая форма калькулятора – «1. Энергии связи ядер». Она позволяет рассчитывать для произвольного ядра или группы ядер следующие параметры:

• энергия связи ядра E_св(A,Z);
• удельная энергия связи ε(A,Z);
• разность δ между энергией связи E_св(A,Z)_exp, полученной экспериментально, и энергией связи E_св(A,Z)_theor, полученной с помощью формулы Вайцзеккера (см. Глава 4, стр. 20 - 25):

δ(A,Z) = E_св(A,Z)_exp - E_св(A,Z)_theor.

    На рис. 22 представлена поисковая форма «1. Энергии связи ядер» калькулятора с примером ее заполнения для формирования предписания по запросу «Определить энергии связи ядер в области значений Z = 80 – 82».
    Формирование этого запросного предписания осуществлено путем внесения конкретных данных в соответствующие разделы поисковой формы следующим образом:

• «Входные параметры» - в раздел “Z” введен диапазон значений «80 - 82», разделы “N” и “A” оставлены пустыми;
• «Варианты расчета»- выбран вариант «Энергия связи»;
• «На оси абсцисс» - по умолчанию оставлен вариант “A”.

    Нажатие кнопки «Вычислить» позволяет рассчитать и получить в виде таблицы соответствующие числовые данные. Фрагмент соответствующей таблицы приведен на рис. 23.
    Нажатие кнопки «Построить график» позволяет получить графическое изображение рассчитанных зависимостей E_св(A,Z) от массового числа ядра A для изотопов c Z = 80 – 82. Графические представления этих зависимостей приведены на рис. 24 вместе с обозначениями использованных программой символов.

Рис. 22. Пример заполнения поисковой формы калькулятора “1. Энергии связи ядер”: формирование запросного предписания для получения энергии связи Eсв (подробности см. в тексте) различных ядер в области Z = 80 - 82.

Рис. 23. Результат работы поисковой формы калькулятора “1. Энергии связи ядер”: в таблице – соответствующие числовые значения энергии связи Eсв в зависимости от массового числа A для ядер с Z = 80 – 82.

Рис. 24. Результат работы поисковой формы калькулятора “1. Энергии связи ядер”: на графике представлены зависимости энергий связи Eсв от массового числа A для ядер с Z = 80 – 82.

    Созданный интерактивный калькулятор позволяет также получать разности значений энергии связи ядер, рассчитываемых по экспериментальным значениям масс и по классической формуле Вайцзеккера.
    Кроме того, возможен и расчет значений удельной энергии связи ε.
    Эти возможности иллюстрируются с помощью рис. 25 и 26.
    На рис. 25 представлен пример формирования с помощью той же поисковой формы «1. Энергии связи ядер» калькулятора предписания для запроса на определение удельной энергии связи и разности экспериментальных и теоретических значений для энергии связи:

• «Входные параметры» - в раздел “Z” введен диапазон значений «30 - 70»;
• «Варианты расчета» - одновременно выбраны варианты:
  «Удельная энергия связи» и
  «Разность энергий связи (Эксперимент – Вайцзеккер)»;
• «На оси абсцисс» - выбран вариант “N”.

На рис. 26 представлены полученные в результате обработки запроса зависимости величин ε(A,Z) и
δ(A,Z) = E_св(A,Z)_exp - E_св(A,Z)_theor. (Эксперимент - Вайцзеккер) от числа нейтронов N для изотопов Z = 30 - 70. Хорошо видны характерные максимумы величины δ(A,Z), проявляющиеся для магических чисел N = 50 и N = 82.
    Следует отметить, что данный рисунок представляет собой по существу «зеркальное отражение» данных для зависимости Δ = E_св(A,Z)_theor, - E_св(A,Z)_exp, приведенных на рис. 8.

Рис. 25. Пример заполнения поисковой формы калькулятора «1. Энергии связи ядер»: формирование запросного предписания для получения величин удельной энергии связи ε(A,Z) и разности δ(A,Z) между экспериментальным и теоретическим значениями энергии связи (подробности см. в тексте) для различных ядер с Z = 30 - 70.

Рис. 26. Результат работы поисковой формы калькулятора – “1. Энергии связи ядер”: зависимости величин ε(A,Z) и δ(A,Z) от числа нейтронов N.

Энергии отделения нуклонов и ядер от ядра (A,Z)

    Энергии отделения протона B_p и нейтрона B_n

    Энергии отделения протонов и нейтронов от ядра (A,Z) могут быть выражены через массы ядра и нуклонов следующим образом:

B_p(A,Z) = [M(A-1,Z-1) + M_p − M(A,Z)]c² = E_св(A,Z) −  E_св(A-1,Z-1);
B_n(A,Z) = [M(A-1,Z) + M_n − M(A,Z)]c² = E_св(A,Z) −  E_св(A-1,Z).

    Ядро перестаёт быть связанным и, следовательно, перестает существовать, когда энергия отделения нуклона становится меньше нуля:

B_n < 0, B_p < 0,

т.е. тогда, когда существование ядра (A,Z) энергетически не выгодно.

На рис. 27 приведена поисковая форма калькулятора «2. Энергии отделения нуклонов и ядер» с примером формирования запросного предписания для определения энергий отделения нейтрона и протона от различных изотопов ядра La с Z = 57:

• «Входные параметры» - введено значение «Z = 57»;
• «Варианты отделения» - введено значение “n,p”;
• «Тип атомных ядер» - выбраны “Все ядра”;
• «На оси абсцисс» - по умолчанию оставлен вариант «А»;
• остальные параметры оставлены по умолчанию.

    На рис. 28 показаны зависимости величин энергии отделения нейтрона B_n(A,Z) и протона B_p(A,Z) от атомной массы ядра A для изотопов лантана La (Z = 57).

Рис. 27. Пример заполнения поисковой формы калькулятора  “2. Энергии отделения нуклонов и ядер”: формирование запросного предписания для определения энергии отделения нейтрона и протона от различных изотопов лантана La (Z = 57).

Рис. 28. Результаты работы поисковой формы калькулятора – “2. Энергии отделения нуклонов и ядер”: зависимости энергии отделения нейтрона Bn(A,Z) и протона Bp(A,Z) от массового числа ядра A для различных изотопов лантана La (Z = 57).

    Сравнивая экспериментальные данные с результатами расчётов на основе различных теоретических моделей, можно изучать применимость этих моделей к описанию характеристик атомных ядер. Приведённые на Рис. 28 данные наглядно демонстрируют эффект спаривания в атомных ядрах.

    Энергия отделения двух нейтронов

    В соответствии с приведенными выше соотношениями для энергии отделения протонов и нейтронов от ядра (A,Z) энергия отделения двух нейтронов может быть выражена через массы начального и конечных ядер, а также нуклонов следующим образом:

B_2n(A,Z)[M(A-2,Z) − M(A,Z) + 2M_n]c² = E_св(A,Z) −  E_св(A-2,Z).

Рис. 29 иллюстрирует использование той же поисковой формы калькулятора “2. Энергии отделения нуклонов и ядер” для формирования запросного предписания по определению энергий отделения двух нейтронов от атомного числа ядра A для различных изотонов ядер с определенными Z:

• «Входные параметры, Z» - введены значения «55, 57, 59, 61, 63, 65»;
• «Варианты отделения» - введено значение “2n”;
• «Тип атомных ядер» - выбраны “Все ядра”;
• «На оси абсцисс» - по умолчанию выбран вариант «А»;
• остальные параметры оставлены по умолчанию.

    Результат обработки запроса по сформированному предписанию приведен на рис. 30.

Рис. 29. Пример заполнения поисковой формы калькулятора – “2. Энергии отделения нуклонов и ядер”: формирование запросного предписания для определения энергии отделения двух нейтронов от различных изотопов ядер с Z = 55, 57, 59, 61, 63, 65.

Рис. 30. Результаты работы поисковой формы калькулятора – “2. Энергии отделения нуклонов и ядер”: зависимости энергии отделения двух нейтронов B2n(A,Z) от массового числа ядра A для различных изотопов ядер с Z = 55, 57, 59, 61, 63, 65.

    Энергия отделения любого количества нуклонов, сложных частиц и ядер от ядра (A,Z)

    Рис. 31 иллюстрирует использование той же поисковой формы калькулятора «2. Энергии отделения нуклонов и ядер» для формирования запросного предписания по определению энергий отделения сложных комбинаций ядер и частиц.
    В рассматриваемом конкретном примере иллюстрируется формирование запроса на определение энергии отделения комбинации ядра ¹³C и протона от различных изотопов ядра Ca:

• «Входные параметры» - введено значение «Z = 20»;
• «Варианты отделения» - заданы значения для комбинации ядра ¹³C и частицы (протона) - “13С+p”;
• «Тип атомных ядер» - выбраны “Все ядра”;
• «На оси абсцисс» - по умолчанию выбран вариант «А»;
• остальные параметры оставлены по умолчанию.

На рис. 32 показаны энергии отделения комбинации ядра и частицы ¹³С + p для различных изотопов Ca (Z = 20) в зависимости от массового числа ядра A.

Рис. 31. Пример заполнения поисковая форма калькулятора – “2. Энергии отделения нуклонов и ядер”: формирование запросного предписания по определению энергии отделения комбинации ядра 13С и протона p от различных изотопов Ca (Z = 20).

Рис. 32. Энергии отделения комбинации ядра 13С и протона p от различных изотопов Ca (Z = 20) в зависимости от массового числа A.

Энергии радиоактивных распадов

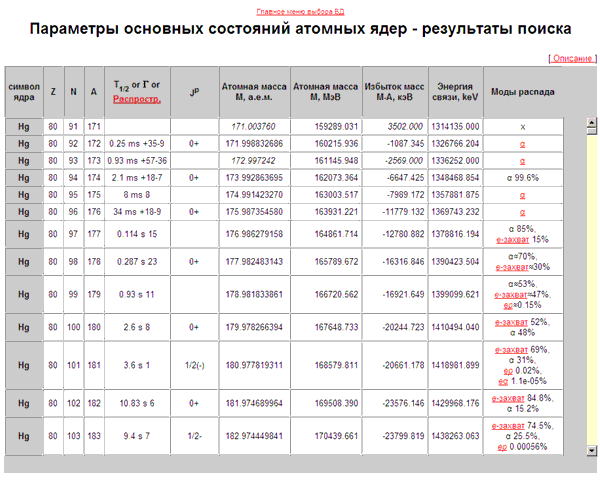
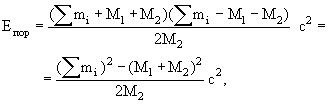    Энергия α-распада Q_α(A,Z)

    Зависимость величины энергии a-распада Q_α(A,Z) от A, Z и N

Q_α(A,Z) = [M(A,Z) − M(A-4,Z-2) − M(4,2)]c²,

позволяет получить информацию об оболочечной структуре атомных ядер.
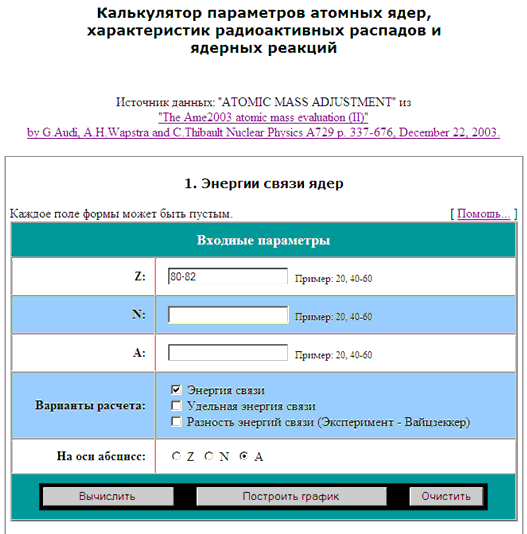
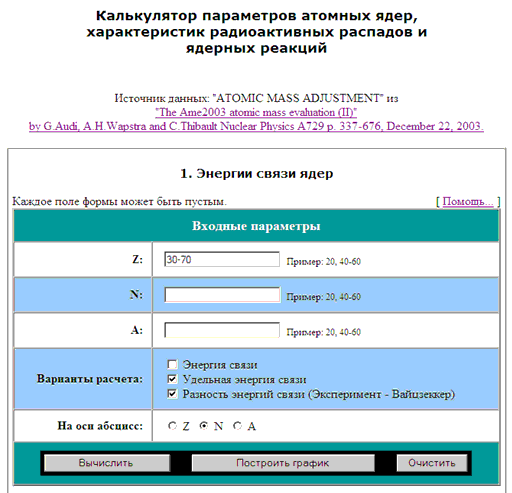
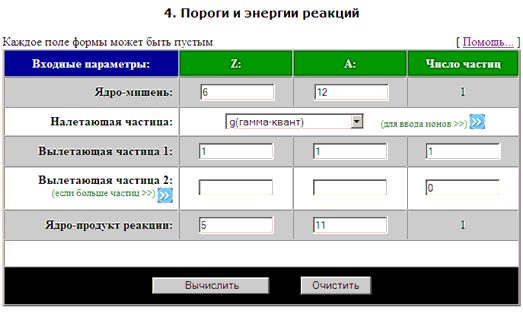
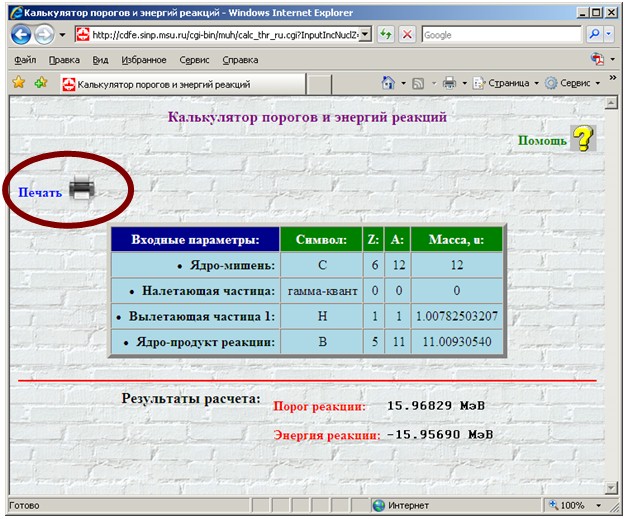
    На рис. 33 приведена поисковая форма «3. Энергии распадов» калькулятора с примером формирования запросного предписания на определение энергий α-распада:

• «Входные параметры» - введены значения «Z = 85, 87, 89, 91, 93»;
• «Тип распада» - в меню выбрано значение “α (альфа-распад)”.
• «На оси абсцисс» - выбран вариант “N”.

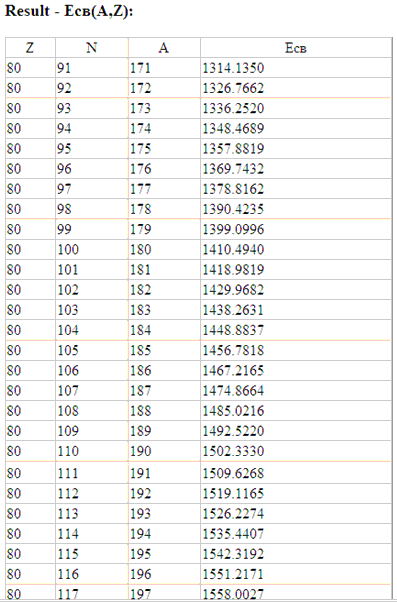
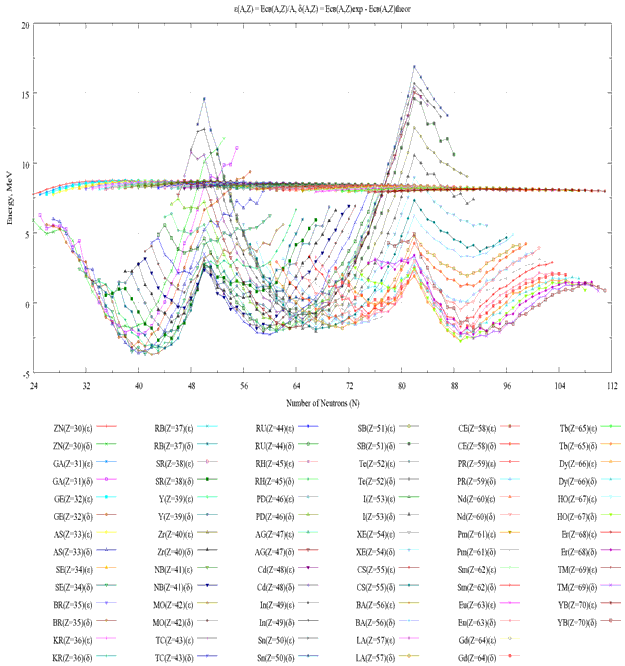
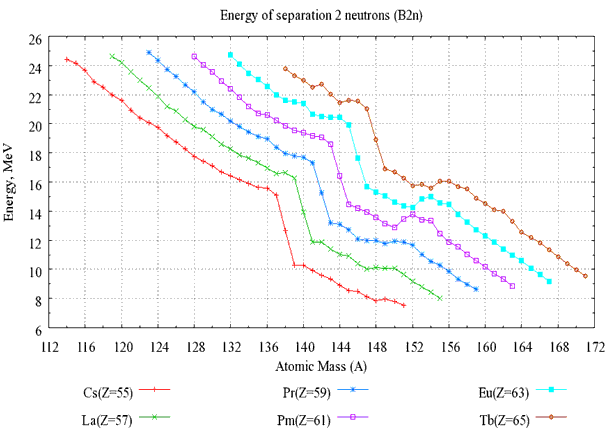
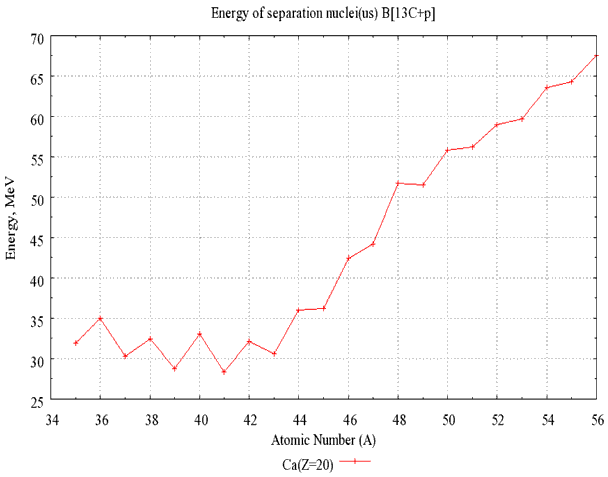
    Рассчитанные зависимости энергии α-распада от числа нейтронов N приведены на рис. 34. Точки, соответствующие различным изотопам, соединены. Данные показывают поведение величины энергии α-распада Q_α(A,Z) для различных изотопов с Z = 85, 87, 89, 91, 93, 95 в районе магического числа нейтронов N = 126. Эта характерная особенность в районе N = 126 (рис. 34)

Q_α(A,Z) = E_св(A-4,Z-2) + E_св(4,2) − E_св(A,Z)

является следствием заполнения нейтронной оболочки.
    Используя эмпирическое соотношение, связывающее период полураспада T_1/2 и энергию α-частицы E_α

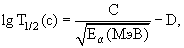
где величины C = 150 и D = 55 мало изменяются для тяжёлых ядер, можно оценить периоды α-распада и сравнить их с экспериментально измеренными значениями.

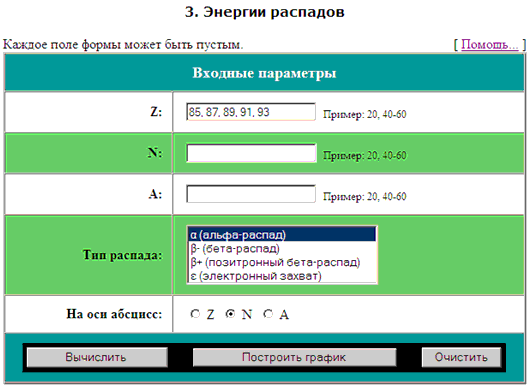
Рис. 33. Пример заполнения поисковой формы калькулятора – «3. Энергии распадов»: формирование запросного предписания на определение энергий α-распада Qα(A,Z) ядер с Z = 85, 87, 89, 91, 93 в зависимости от числа нейтронов N.

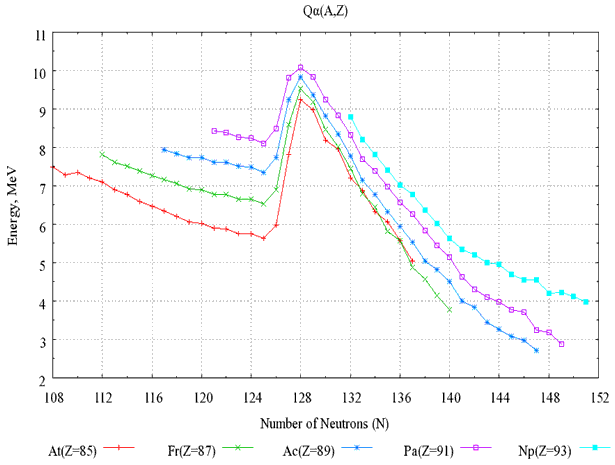
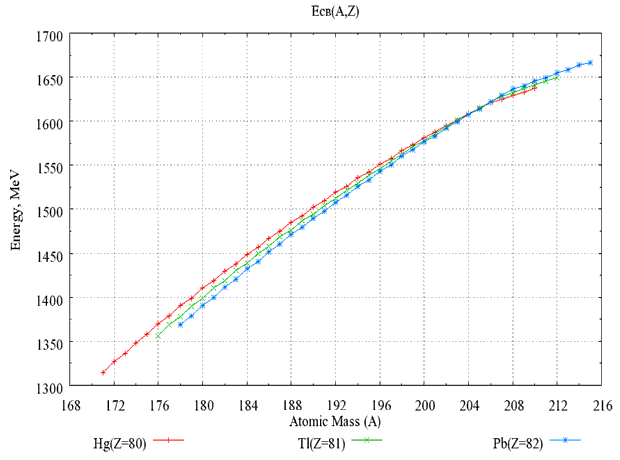
Рис. 34. Зависимости энергии α-распада Qα(A,Z) изотопов с Z = 85, 87, 89, 91, 93 от числа нейтронов N.

    Энергия β-распада

    Явление β-распада состоит в том, что ядро (A,Z) самопроизвольно испускает лептоны 1-го поколения - электрон (или позитрон), электронное нейтрино (или антинейтрино), переходя при этом в ядро-изобару с тем же массовым числом A, но с атомным номером Z, на единицу большим или меньшим.
    Существуют три типа β-распада, схемы которых выглядят следующим образом:

• β^--распад: (A,Z) → (A,Z+1) + e^- + _e,
• β⁺-распад: (A,Z) → (A,Z–1) + e⁺ + ν_e,
• e-захват: .(A,Z) + e^- → (A,Z–1) + ν_e,

    Главной особенностью β-распада является то, что он обусловлен слабым взаимодействием. Бета-распад – процесс не внутриядерный, а внутринуклонный. В ядре распадается одиночный нуклон.
    Происходящие при этом внутри ядра превращения нуклонов и энергетические условия соответствующего типа β-распада выглядят так (массу нейтрино полагаем нулевой):

• β^--распад – M_N(A,Z) > M_N(A,Z+1) + m_e,
• β⁺-распад – M_N(A,Z) > M_N(A,Z–1) + m_e,
• e-захват – M_N(A,Z) + m_e > M_N(A,Z–1),

где M_N(A,Z), M_N(A,Z+1) и M_N(A,Z–1) – массы ядер.
    При e-захвате ядро (A,Z) поглощает один из электронов атомной оболочки (обычно ближайшей к нему K-оболочки), испуская электронное нейтрино.
    Из приведенных соотношений для энергий β⁺-распада и e-захвата видно, что во всех случаях, когда возможен β⁺-распад, одновременно возможен и e-захват. Это – два конкурирующих между собой процесса. Если массы начального ядра M_N(A,Z) и конечного ядра M_N(A,Z–1) одновременно удовлетворяют неравенствам

M_N(A,Z) + m_e > M_N(A,Z–1),
M_N(A,Z) < M_N(A,Z–1) + m_e,

то e-захват разрешен, а β⁺-распад запрещен.
    В масс-спектроскопических измерениях обычно приводятся не массы ядер M_N(A,Z), M_N(A,Z+1), M_N(A,Z–1), а массы атомов M(A,Z), M(A,Z+1), M(A,Z–1). Масса атома связана с массой ядра следующим образом (энергия связи электронов здесь не учитывается):

M(A,Z) = M_N(A,Z) + Zm_e,

Энергия, выделяющаяся при β-распаде ядра (A,Z), выражается через параметры ядер и атомов:

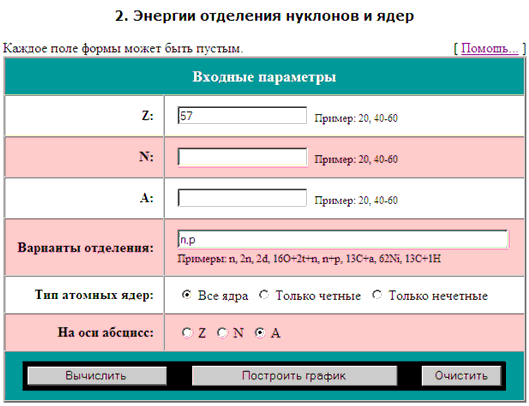
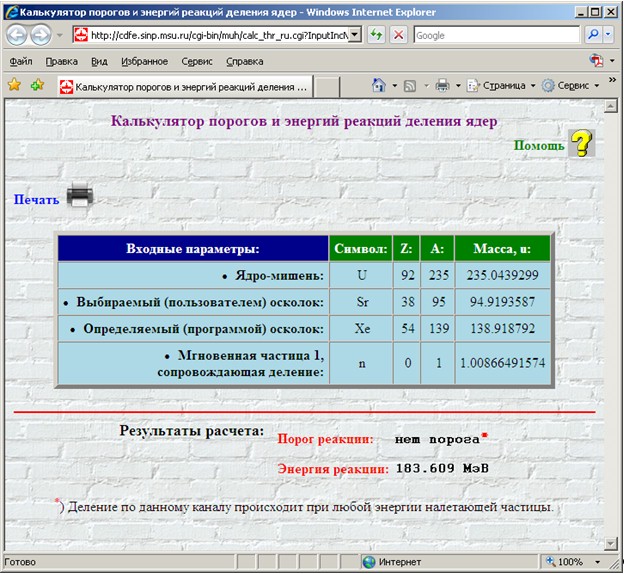
    На рис. 35 приведена поисковая форма калькулятора «3. Энергии распадов» с примером формирования запросного предписания на определение энергий Q_β-(A,Z) β^--распада нескольких ядер:

• -        «Входные параметры, Z» - заданы значения «81 – 83»;
• -        «Тип распада» - задано значение “β^- (бета-распад)”;
• -        «На оси абсцисс» - выбран вариант «N»;
• -        остальные параметры оставлены по умолчанию.

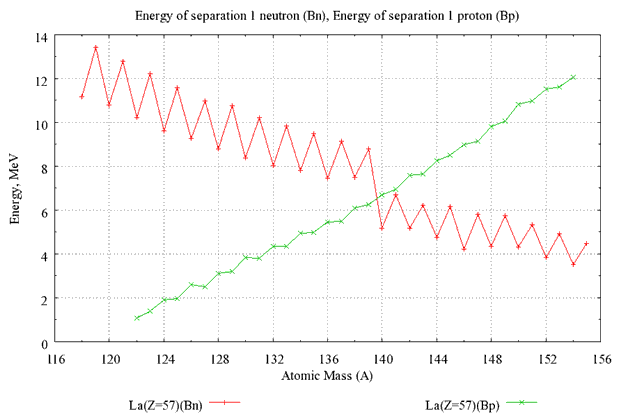
На рис. 36, приведены величины Q_β-(A,Z) энергии β^--распада для различных ядер с Z = 81 – 83. Изотопы с одинаковым значением Z соединены сплошной линией.

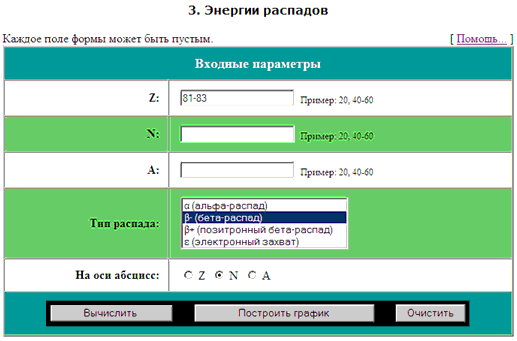
Рис. 35. Пример заполнения поисковой формы калькулятора – “3. Энергии распадов”: запросное предписание по определению энергий β--распада Qβ-(A,Z) ядер c Z = 81 – 83.

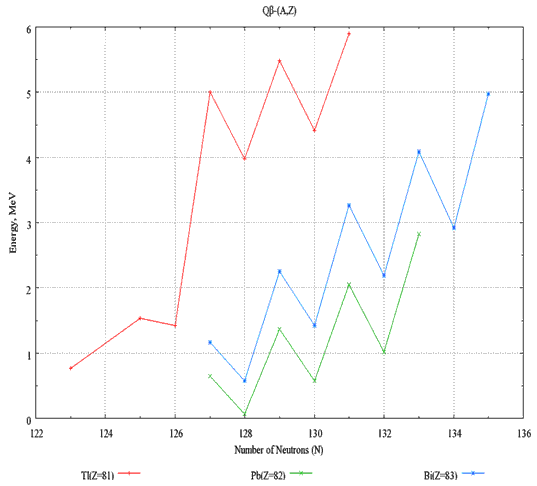
Рис. 36. Зависимости энергии β--распада Qβ- от числа нейтронов N для ядер с Z = 81 – 83.

Порог ядерной реакции

    Порог ядерной реакции Е_пор – минимальная кинетическая энергия налетающих частицы или атомного ядра, при которой осуществляется реакция, идущая с поглощением энергии.
    В случае, когда ядро массы M₁ налетает на покоящееся ядро массы M₂ и образуются частицы с массами m_i, порог реакции:

или

где Q = (M₁ + M₂ – ∑m_i)c² – энергия реакции, а  ∑m_i – сумма масс частиц, образующихся в результате ядерной реакции.
    В ядерной физике |Q| << 2M₂c²,

    На рис. 37 приведена поисковая форма калькулятора – “4. Пороги и энергии реакций” для определения значений порога Е_порог и энергии Q для ядерной реакции ¹²C(γ,p)¹¹B:

• «Ядро – мишень» - ¹²C (выбраны значения Z = 6, A = 12);
• «Налетающая частица» - в выпадающем меню выбран гамма–квант;
• «Вылетающая частица 1» - p, протон (выбраны значения Z = 1, A = 1, «Число частиц» – 1); при необходимости могут быть выбраны «Вылетающая частица 2», а также – большее число (до 6) частиц (следует использовать специальную кнопку «>>», повторное нажатие кнопки приводит к возврату в исходную форму с двумя налетающими частицами);
• «Ядро-продукт реакции» – ¹¹B (Z = 5 (6 – 1), A = 11 (12 - 1) – определяются программой).

    На рис. 38 приведена выходная форма запроса: приведены результаты расчета порога и энергии реакции ¹²C(γ,p)¹¹B, а кроме того указаны все заданные характеристики ядра-мишени, налетающей и вылетающих частиц и рассчитанные программой характеристики ядра-продукта реакции.
    Полученные результаты можно распечатать с помощью кнопки “Печать” (значок принтера в левом верхнем углу экрана – например, на рис. 38).

Рис. 37. Пример заполнения поисковой формы калькулятора – “4. Пороги и энергии реакций”: формирование запроса на определение порога Епор и энергии Q реакции 12C(γ,p)11B.

Рис. 38. Результаты работы поисковой формы калькулятора – “4. Пороги и энергии реакций” по определению порога Епор и энергии Q реакции 12C(γ,p)11B.

Энергия деления ядер

    То, что при делении тяжёлых ядер выделяется энергия, непосредственно следует из зависимости удельной энергии связи ε = E_св(A,Z)/A от массового числа А (рис. 7). При делении тяжёлого ядра образуются более лёгкие ядра, в которых нуклоны связаны сильнее, и часть энергии  при делении высвобождается.
    Как правило,  деление ядер  сопровождается вылетом 1 – 4 нейтронов.
    Выразим энергию деления Q_дел через энергии связи начального и конечных ядер. Энергию начального ядра, состоящего из Z протонов и N нейтронов, и имеющего массу M (A,Z) и энергию связи E_св(A,Z), запишем в следующем виде:

M(A,Z)c² = (Zm_p + Nm_n)c² - E_св(A,Z).

    Деление ядра (A,Z) на 2 осколка (A₁,Z₁) и (А₂,Z₂) сопровождается образованием N_n = A – A₁ – A₂ мгновенных нейтронов. Если ядро (A,Z) разделилось на осколки с массами M₁(A₁,Z₁), M₂(A₂,Z₂) и энергиями связи E_св1(A₁,Z₁), E_св2(A₂,Z₂), то для энергии деления имеем выражение:

Q_дел = {M(A,Z) – [M₁(A₁,Z₁) + M₂(A₂,Z₂) + (A – A₁ – A₂)m_n]}c² = E_св1(A₁,Z₁) + E_св(A₂,Z₂) – E_св(A,Z),

причём

A = A₁ + A₂ + N_n, Z = Z₁ + Z₂.

    На рис. 39 приведена поисковая форма калькулятора “5. Деление ядер” с примером формирования поискового предписания по определению энергетического порога и энергии реакции спонтанного деления ядра ²³⁵U с образованием осколка ¹³⁹Xe и вылетом одного нейтрона.
    Формирование запросного предписания осуществлено следующим образом:

• «Ядро – мишень» - ²³⁵U (выбраны значения Z = 92, A = 235);
• «Налетающая частица» - налетающих частиц нет – спонтанное деление (в выпадающем меню выбрано «Нет налетающих частиц»);
• «Выбираемый (пользователем) осколок» – ядро-осколок, например, ⁹⁵Sr (выбраны значения Z = 38, A = 95);
• «Определяемый (программой) осколок» – ядро-осколок ¹⁴⁰Xe (Z = 92 – 38 = 54, A = 235 – 95 = 140);
• «Мгновенная частица 1, сопровождающая деление» - n, нейтрон (выбраны значения Z = 0, A = 1, «Число частиц» - 1); при этом меняются характеристики определяемого программой осколка – ¹³⁹Xe (Z = 54, A = 140 – 1 = 149);

    На рис. 40 приведена выходная форма данного запроса: видно, что энергетический порог при делении ядра ²³⁵U отсутствует (согласно данным Таблицы, приведенной в Приложении, ядро ²³⁵U имеет моду распада – “Испускание нейтрона”).

http://cdfe.sinp.msu.ru/services/calc_thr/calc_thr_ru.html#5

 

Рис. 39. Пример заполнения поисковой формы калькулятора – “5. Деление ядер”: формирование запроса для определения энергии порога Епор и энергии Q реакции спонтанного деления ядра 235U с образованием осколков 139Xe (выбран пользователем) и 95Sr (определен программой) и вылетом одного нейтрона.

Рис. 40. Результаты работы поисковой формы калькулятора – “5. Деление ядер” по определению порога Епор и энергии Q спонтанного деления ядра 235U с образованием осколков 95Sr (выбран пользователем) и 139Xe (определен программой) и вылетом одного нейтрона.