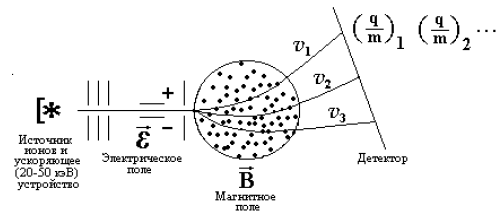
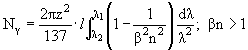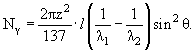6. Способы измерения масс частиц и ядерОсновной физической величиной в физике частиц и ядер является их масса. Рассмотрим некоторые способы определения масс частиц и ядер. Во всех этих способах в качестве детекторов используются приборы, работа которых основана на электромагнитных взаимодействиях. 6.1. Метод определения масс ядер − масс-спектроскопия На рис. 42 представлена схема масс-спектрометра.
Для элементарных частиц из-за разброса в скоростях этот метод неприменим. 6.2. Методы определения масс элементарных частиц Методы основаны на следующих соотношениях: 6.2.1. Метод времени пролета − определение скорости частицы
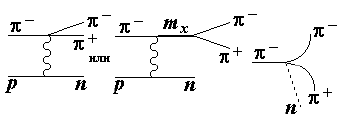
6.2.2. Метод инвариантных масс Метод применяется для частиц со временем жизни τ < 10-16 с. К этому классу
частиц относятся резонансы, а также промежуточные состояния неизвестных частиц с
массой mх, быстро распадающихся на регистрируемые частицы.
Например, для реакции π-р → π+π-n определяется инвариантная масса частиц π+π- с использованием соотношения
Инвариантная масса двух частиц
На опыте определяются
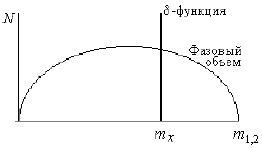
Резонансный всплеск на фоне плавного распределения по фазовому объему
свидетельствует о рождении π+π--мезонов через промежуточное
состояние m12 (рис. 43).
В первых экспериментах по обна-ружению J/ψ-частиц, состоящих из сс-кварков, были определены mJ/ψ = 3000 МэВ, mJ1 = 3770 МэВ, mJ2 = 4040 МэВ. Обнаруженная система получила название кваркония и в последующем изучалась очень детально. Используя соотношение неопределенностей Δt·ΔE ≥ ћ, можно определить время жизни зарегистрированных частиц. ΔЕ = Г = ћ/τ есть
полуширина резонансной кривой, отсюда
Аналогичный метод может быть использован в физике ядра при анализе быстро протекающих ядерных процессов:
В этой реакции короткоживущим ядром является 8Ве. Для него τВе ~ 2·10-16 с
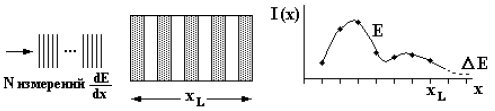
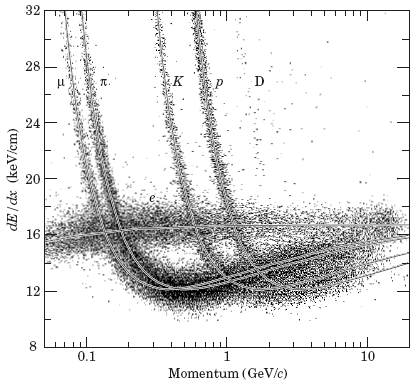
(рис. 45). 6.2.3. Метод многократного измерения ионизационных потерьОпределяется γ и Е, a m = E/γ. Для измерения Лоренц-фактора γ может быть использована формула Бете-Блоха, дающая зависимость ионизационных потерь энергии от скорости частицы (т.е. от Лоренц-фактора
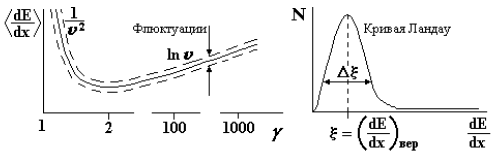
Формула Бете-Блоха представляет средние ионизационные потери, флюктуации вокруг которых описываются распределением Ландау (рис. 46). Для определения на опыте этого распределения используются многослойные детекторы ионизационных потерь. От числа слоев детектора зависит точность определения распределения Ландау и, следовательно, точность определения dE/dx. Зная потери энергии на ионизацию <dE/dx> можно определить Лоренц-фактор γ. Погрешность измерения Δ(dE/dx) ~ N-1/2, где N − число измерений величины dE/dx в многослойном счетчике или в фотоэмульсии. Чем больше N, тем точнее определяется -dE/dx и <dE/dx> − среднее значение, по которому определяется γ.
Рис. 46. Зависимость средних ионизационных потерь от Лоренц-фактора γ и кривая Ландау, описывающая флюктуации ионизационных потерь вокруг среднего значения. Энергия Е измеряется другим способом, например по ионизационному калориметру:
Рис. 47. Схематическое представление установки для измерения потерь энергии в
многослойном счетчике (N измерений dE/dx) и энергии в ионизационном калориметре XL,
с использованием каскадной кривой, описывающей ядерно-каскадный процесс в
калориметре. Энергия
Ядерно-каскадный процесс в калориметре происходит в результате множественного процесса рождения вторичных частиц в реакции р + А → π±,0 + K±,0 + Λ0 + p В этой реакции энергия сталкивающихся частиц передается большому числу
вторичных π+-, π-- и π0-мезонов, а также другим частицам. Ядерно-каскадный
процесс развивается в веществе калориметра за счет вторичных процессов. При этом π0-мезоны, распадающиеся на два фотона, дают начало электромагнитному каскаду,
а π+-, π--мезоны и другие частицы передают энергию вторичным ядерным каскадам.
Как правило, ионизационный калориметр состоит из большого числа детекторов,
прослоенных тяжелым веществом (железом или свинцом). Отклики детекторов под
каждым слоем вещества Ix регистрируются. Чтобы вся энергия соударяющихся частиц
была зарегистрирована, полная длина калориметра должна содержать несколько
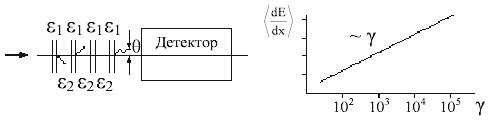
ядерных пробегов до взаимодействия. 6.2.4. Переходное излучениеДля определения Лоренц-фактора γ может служить переходное излучение. Потери энергии на переходное излучение пропорциональны Лоренц-фактору. Переходное излучение возникает на границе раздела двух сред, имеющих разные диэлектрические постоянные ε1 и ε2 (рис. 48).
Рис. 48. Детектор переходного излучения и зависимость средних потерь энергии на переходное излучение от Лоренц-фактора γ. Чтобы количество фотонов, испущенных на границе двух сред, было достаточно
высоким для регистрации, увеличивается количество излучающих слоев.
В табл. 15 представлена энергия <Eγ>, излученная электроном с импульсом ре в установке, состоящей из
650 слоев литиевой фольги толщиной 60 мк каждый с воздушным промежутком между
ними 250 мк.
6.2.5. Черенковское излучение
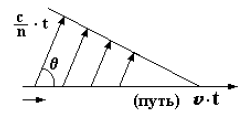
Для определения скорости частиц используется Черенковское излучение.
c/n − скорость света в среде, n − показатель преломления, v − скорость частицы, t
− время. Чаще всего используются пороговые черенковские счетчики, для которых β >
1/n. В пороговых черенковских счетчиках регистрируется только факт испускания
черенковского свечения, когда скорость частицы превышает пороговую скорость.
на пути l в диапазоне длин волн λ1 и λ2.
Дифференциальные черенковские счетчики имеют точность измерения скорости Δβ/β
~7·10-8 при l ~ 700 см и λ ~ 5·10-5 см. 6.3. Детекторы в физике частиц и ядерВ физике частиц и ядер для регистрации ионизующего излучения используются разнообразные детекторы частиц. 6.3.1. Сцинтилляторы
6.3.2. Черенковские детекторы Черенковские детекторы используют разные свойства черенковского
излучения. 6.3.3. Детекторы переходного излученияПереходное излучение, возникающее на границе раздела двух сред в направлении движения частицы с лоренц-фактором γ > 1000, регистрируется детекторами, чувствительными к фотонам в диапазоне энергий 2÷20 кэВ. Детекторы переходного излучения (Transition Radiation Detectors − TRD) используются обычно для разделения электронов и пионов в диапазоне импульсов 0.5 ГэВ/с < р < 100 ГэВ/с. 6.3.4. Многонитные камерыМногонитные камеры (Multy Wire Proportional Chambers − MWPC) содержат десятки и сотни нитей, расположенных на малых (~ 1-2 мм) расстояниях друг от друга. Каждая нить работает независимо и настраивается на регистрацию большей части заряда, образованного в объеме, наполненном газовой смесью. Заряженная частица, проходящая через газовый слой толщиной δ, образует вдоль своего пути электрон-ионные пары. Электроны, образованные в объеме, собираются на нить за несколько наносекунд. Положительные ионы движутся от нити на катод и генерируют сигнал, который регистрируется через некоторое время t
где q − положительный заряд, С − емкость между анодной нитью и катодом, F(t) = ln(l + t/t0)/ln(l + tmax/t0), t0 − это одна или несколько наносекунд, £тах − это время сбора ионов на катод. 6.3.5. Кремниевые полупроводниковые детекторыПолупроводниковые детекторы широко применяются в современной экспериментальной физике высоких энергий. Они служат для высокоточного разрешения вершин взаимодействия, а также в трековых детекторах и как фотодетекторы в сцинтилляционных калориметрах. В качестве основного материала используются кремний, галлий-арсенит и др. На основе полупроводниковых детекторов создаются микростриповые детекторы с высоким пространственным разрешением. Для этих детекторов обычно требуется низкошумящая электроника. 6.3.6. Времяпроекционные камеры Типичная газонаполненная времяпроекционная камера (Time Proection Chamber
−
ТРС) состоит из длинной однородной дрейфовой области (1-2 метра), центральной
высоковольтной многоанодной мембраны, анодных нитей и катодных плоскостей.
Магнитное поле прикладывается параллельно направлению дрейфа электронов,
возникающих при движении частицы в объеме камеры. Многократные измерения dE/dx вдоль траектории частицы комбинируются с измерениями импульса в магнитном поле и
создают прекрасные условия для идентификации частиц.
Рис. 49. Результат измерения ионизации в газонаполненной ТРС для частиц разной природы в зависимости от импульса. 6.3.7. Калориметры В электромагнитных калориметрах в качестве детекторов используются кристаллы
натрий-йод (Nal), свинцовые стекла, жидкий аргон в сочетании со свинцовыми пластинами, вольфрамат свинца толщиной, достаточной
для поглощения электромагнитного каскада. Для рр-соударений X = 21.7, Y = 98.39. Таблица 16. Поперечные сечения и средние свободные пробеги
Связь между λ и σ:
При этом использовалась зависимость поперечных сечений от атомного номера ядра А в виде: σT = σppА0.77, σinel = σppА0.71. Вычисления средних свободных пробегов выполнены для энергий в интервале Е ~ 80÷240 ГэВ. 6.3.8. Сверхпроводящие соленоиды для коллайдерных детекторовСверхпроводящие соленоиды обозначены именами соответствующих экспериментов, выполняемых на ускорителях в Фермиевской и Стэнфордской национальных лабораториях (США), в Европейском центре ядерных исследований (ЦЕРН, Швейцария), в Гамбургском ускорительном центре (Германия): CDF, DO, BaBar, TOPAZ, VENUS, CLEO, ALEPH, Для измерения импульсов частиц по кривизне траектории в однородном магнитном поле используются следующие соотношения: pcosλ = О.ЗВρ, где p − импульс (ГэВ/с), В − магнитное поле (Гаусс), ρ − радиус кривизны (м), А − пинч-угол. Литература
|
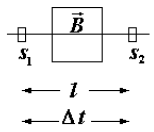 Время пролета Δt определяется тем
точнее, чем меньше скорость v, и лежит в интервале τ > 10-6÷10-7 с.
v = l/Δt. Импульс
Время пролета Δt определяется тем
точнее, чем меньше скорость v, и лежит в интервале τ > 10-6÷10-7 с.
v = l/Δt. Импульс
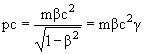 .
.
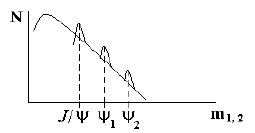
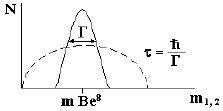
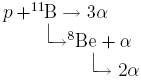
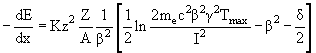
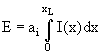 (рис. 47).
(рис. 47).