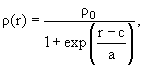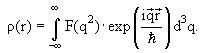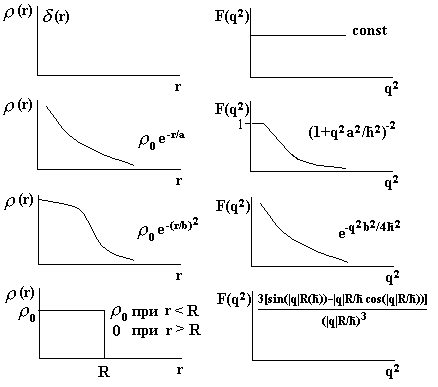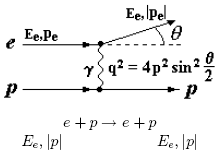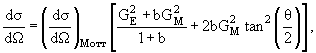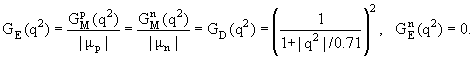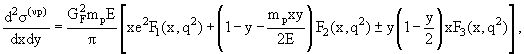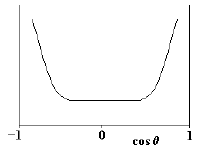7. Структура материиДля исследования структуры материи следует простейшую частицу направлять на частицу более сложную, структура которой неизвестна. Этот метод впервые использовал Э.Резерфорд в 1911 году, когда α-частицу стал рассеивать на атоме и обнаружил атомное ядро. Сейчас нам известны бесструктурные частицы: е, μ, τ и их нейтрино, и мы можем изучать структуру материи, используя эти бесструктурные объекты. 7.1. Электрон − точечная частица Сначала посмотрим, как было доказано, что лептоны не имеют структуры, т.е.
являются истинно элементарными − иными словами, фундаментальными частицами.
По теории Дирака для точечной частицы
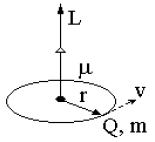
Рассмотрим классический пример определения магнитного момента заряженной
частицы (рис. 50). Магнитный момент электрона складывается из нормального и аномального
магнитных моментов. Нормальный магнитный момент определяется магнетоном Бора,
аномальный магнитный момент возникает из-за квантово-электродинамических
поправок.
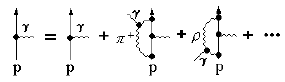
Реальный электрон, окруженный электрическим полем, испускает и поглощает
фотоны. Испущенный фотон может образовать виртуальную электрон-позитронную пару.
Такой процесс многократно повторяется. Его описание можно представить в виде
разложения по степеням константы взаимодействия αе. а = (|g| − 2)/2; для электрона Дирака a = 0, т.к. g = 2. По КЭД расчет атеор с использованием разложения по степеням α соответствует расстояниям до 10-16 см.
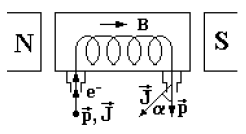
Определение величины ае на опыте может быть осуществлено при изучении
движения электрона в магнитном поле В (рис. 51). Постановка опыта состоит в
следующем: между полюсами магнита N и S располагается сосуд, из которого выкачан
воздух. В сосуд впускается электрон, спин которого направлен по импульсу
Если g = 2, то в однородном магнитном поле угол
Сравнение атеор и аэксп дается величиной ξ
Ничтожное различие между теоретическим и экспериментальным значением величины ае позволяет сделать вывод, что вплоть до расстояния 10-16 см электрон − точечная частица.
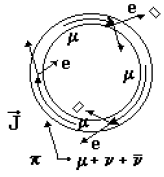
Эксперимент для измерения величины аμ = [(g-2)/2]μ (рис. 52) выполнялся на
циклотроне радиусом 7 м в Брукхейвенской национальной лаборатории (США). Мюоны
накапливались в кольце с магнитным полем В = 1.47 Тс, создаваемым 40
электромагнитами. Мюоны возникали от распада пионов с импульсом 3.098 ГэВ/с по
каналу π± → μ± + ν(
Расчетное значение аμ получилось следующим:
Для электрона ае определяется числом диаграмм Фейнмана, учитывающих
квантово-электродинамические поправки, и точность вычисления можно увеличить,
увеличив число диаграмм (например, для электрона член Сеα4 включает 891
диаграмму). Для мюона при вычислении ам требуется учитывать эффекты,
происходящие на меньших расстояниях (из-за большей массы мюона mμ ~ 200
mе).
Такими эффектами являются слабые радиационные и адронные поправки. По оценкам aμcл
~ 20·10-10 , aμадр ~ 702(9)·10-10, аμКЭД
~ 11658480.(3)·10-10 и эти поправки
известны с плохой точностью (γ → е+е- и γ → h+h- − адронная
поправка).
Высокая степень согласия расчетов на основе КЭД с экспериментом подтверждает
надежность этой теории.
Реальный протон окружен облаком виртуальных пионов. Пионы отвечают за структуру "внешних" частей облака вокруг "голого" протона. Поглощение и испускание пионов может происходить на расстояниях порядка комптоновской длины волны пиона λπ ~ ћ/mπc и реально на расстоянии λπ ~ 0.7 фм. Магнитные моменты некоторых барионов: μΣ = (−1.157 ±0.025)μN; Измерения магнитных моментов барионов показывают, что барионы имеют
структуру. 7.2. Определение размеров ядер Наилучшим способом изучения структуры частиц являются эксперименты по
рассеянию бесструктурных частиц на структурных (типа опытов Резерфорда).
Дальнейшее изучение структуры атомных ядер проводилось в Стэнфордской национальной лаборатории в экспериментах по рассеянию электронов на разных атомных ядрах.
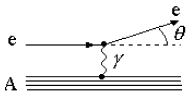
Это были эксперименты Хофштадтера, в которых изучалось распределение электрического заряда во всех ядрах периодической системы элементов. Отличие опытов Хофштадтера от экспериментов Резерфорда состоит в том,
что он использовал электроны, которые имеют спин 1/2ћ и не имеют структуры
(рис. 53).
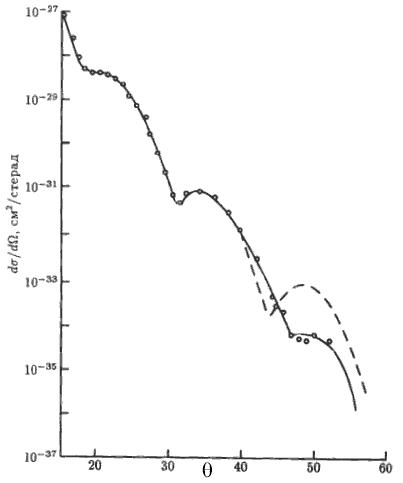
Упругое рассеяние электрона на протяженном объекте, каковым является ядро, может быть представлено следующим соотношением:
где F(q2) − форм-фактор ядра,
Можно определить среднеквадратичный радиус ядра: <r2> = ∫ρ(r)r2d3r.
В результате многочисленных измерений было определено распределение плотности электрического заряда в разных ядрах. Для ядер Са и Рb оно показано на рис. 54 и для ядра Са может быть аппроксимировано в виде ρ(r):
где ρ0 = 0.17 нукл/фм3, с = (1.18А1/3 − 0.48) фм − радиус половинной
плотности, t = 4ln3 = 2.4 фм − толщина поверхностного слоя ядра,
Радиусы ядер с атомным номером А определяются соотношением
В описанной процедуре возникают неопределенности, связанные с использованием
бесконечных пределов при интегрировании, в то время как на опыте эти пределы
всегда конечны. Кроме того, переход от экспериментально измеренного квадрата
форм-фактора к форм-фактору также создает неопределенность. Поэтому поступают
иначе:
7.3 Структура нуклона7.3.1 Упругое рассеяние
Классические эксперименты по изучению структуры нуклона были выполнены американским физиком В.К. Панофски в 1964 году в Стэнфордской национальной лаборатории (СЛАК, США). Изучалось упругое рассеяние электронов на протонах. Измерялся угол отклонения электрона после упругого взаимодействия (рис. 57). На опыте измерялось эффективное сечение рассеяния в зависимости от квадрата переданного импульса q2. Учитывая, что у протона существуют электрический и магнитный форм-факторы, сечение может быть представлено в виде:
b = −q2/4m2c2, где m − масса нуклона, θ − угол рассеяния, −q2
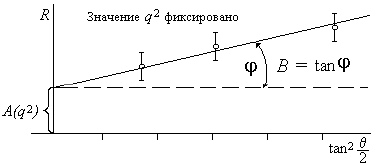
− При q2 = 0 GE(q2 = 0) = q/e, GM(q2 = 0) = M/μN. GpE(0) = 1, GnE(0) = 0; Для удобства анализа рассматривается отношение R (формула Розенблата). R = (dσ/dΩ)/(dσ/dΩ)Мотт = A(q2) + B(q2)tan2(θ/2); Зависимость R от tan2(θ/2) изображается прямой линией (рис. 58)
Как видно из рисунка, значения A(q2) и B(q2) могут быть определены и, таким
образом, можно вычислить форм-факторы GE и GM в зависимости от q2.
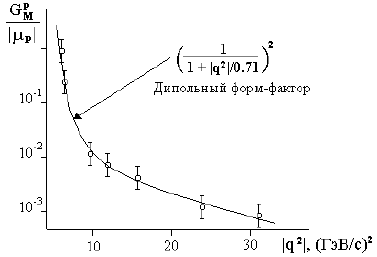
Оказалось, что зависимости магнитного форм-фактора для протона и нейтрона
одинаковы и их стали называть дипольным форм-фактором.
Дипольный форм-фактор оказался зависящим от q2 Это свидетельствует о том,
что протоны и нейтроны не являются точечными объектами, а имеют протяженную
структуру. Распределение плотности р{г) для протона не описывается средним
распределением, а хорошо аппроксимируется функцией ρ(r) = ρ0ехр(r/а) где а =
ћ/q0 = 0.23 фм. Из этой формулы следует, что протон не имеет резко очерченных
границ, причем среднеквадратичные радиусы распределения электрического заряда и
намагниченности практически равны: <r2Е>р = (r2M)р
= (r2M)n = 0.7 фм2. Значение
радиуса протона, полученного в расчетах, в которых предполагалось, что протон
окружен облаком виртуальных пионов, качественно согласуется с этой величиной.
Определение среднеквадратичного радиуса нейтрона <r2Е>n экспериментально
затруднено из-за того, что приходится работать с мишенью из дейтерия, а потом
вычитать из полученных величин значения радиусов для протонов. Тем не менее
получено, что <r2Е>n = 0.008 ±0.006 фм2. Отсюда следует, что нейтрон намагничен,
но почти не содержит электрического заряда.
Дальнейшее изучение внутренней структуры протона было выполнено в той же лаборатории в Стэнфорде в экспериментах по глубоконеупругому рассеянию электронов на протонах. 7.3.2. Глубоконеупругое рассеяние Разница между упругим и неупругим процессами соударения состоит в том, что
при упругом рассеянии новые частицы не возникают и энергия электрона после
рассеяния остается без изменений (изменяется только направление вылета электрона
после столкновения), а при неупругом процессе рождаются новые частицы. Энергия,
унесенная новыми частицами, может быть определена по энергии электрона после
взаимодействия Е'. В случае неупругого процесса следует рассматривать двойное
дифференциальное сечение d2σ/dEdΩ в зависимости от q2.
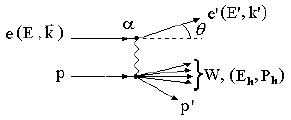
Глубоконеупругое рассеяние можно представить как двухчастичный
процесс: е + р = е' + р' + W. Степень возбуждения протона электроном определяется величиной W(Eh,Ph). На опыте измеряются угол отклонения электрона
θ, энергия Е' и импульс к' электрона после взаимодействия с протоном. Этих данных
достаточно, чтобы вычислить степень возбуждения протона после соударения с
электроном, используя законы сохранения энергии и импульса и приведенные ниже
формулы: ν = Е − Е' − энергия, которую теряет электрон; W2 = Е2h - (
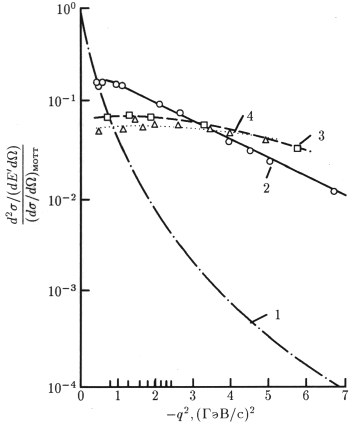
На рис. 61 показано дважды дифференциальное сечение
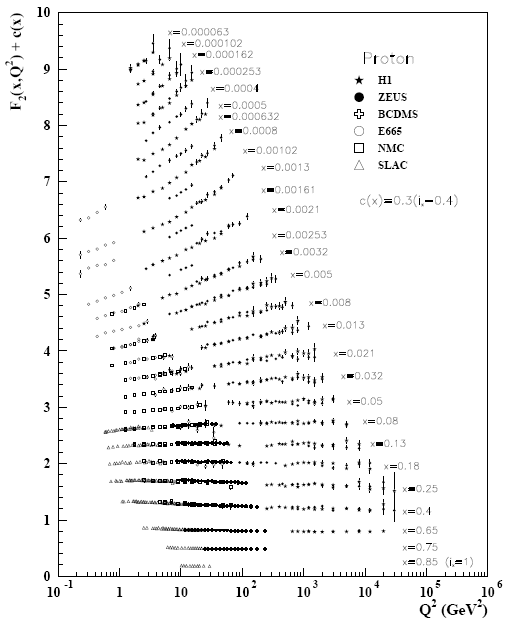
где х = q/2mpν, у = 1 − cos2(θ*/2). В том случае, когда взаимодействуют точечные объекты, F1, F2, F3 не зависят от q2, а являются функцией только безразмерной величины х, причем функции F2 и F1 связаны соотношением Каллана-Гросса F2 = х·F1, т.е. не являются независимыми. На рис. 62 изображены структурные функции протона F2 в зависимости от q2 и для разных значений переменной х.
Рис. 62: Протонная структурная функция F2, измеренная в электромагнитном рассеянии электронов и мюонов для х > 0.00003. Q2 = −q2. Независимость F2 от Q2 наблюдается для х от 0.008 до 0.85. Отсутствие зависимости этих распределений от q2 при х > 0.02
свидетельствует о точечности объектов, на которых происходит рассеяние.
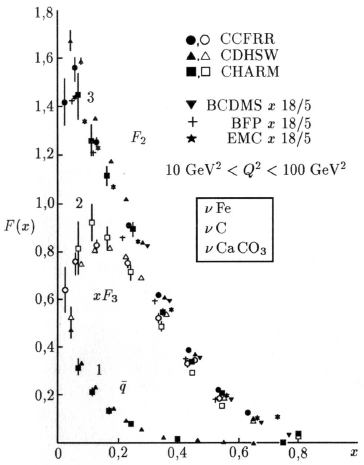
Рис. 63: Спектры партонов в нуклоне в зависимости от доли энергии, уносимой
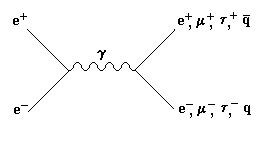
партоном, 7.4. Свойства кварков и глюонов из экспериментов по е+е--аннигиляцииДетальное изучение свойств партонов − кварков и глюонов − было выполнено при столкновении электронов с позитронами. Такие эксперименты проводились на ускорительном комплексе в Гамбурге (Германия) и в С ЛАК (США). 7.4.1. Спин кварка В процессе е+е- могут образовываться пары лептонов (е+е-,
μ+μ-, τ+τ-). В
результате этого процесса образуются также пары кварков q
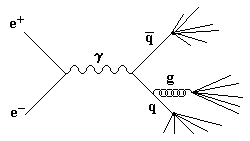
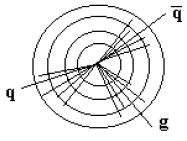
Рис. 64: Процесс аннигиляции: а − диаграмма процесса аннигиляции е+е- в лептоны и кварки; б − угловое распределение лептонов и осей кварковых струй в процессе е+е--аннигиляции. Угловое распределение лептонов (е, μ, τ) (рис. 646), имеющих спин (1/2)ћ, описывается соотношением dσ/dΩ ≈(1 + cos2θ). Оказалось, что угловое распределение осей кварковых струй описывается такой же зависимостью. Таким образом, было показано, что спин кварка J = (l/2)ћ. 7.4.2 Рождение глюонных струй как следствие излучения глюона кваркомНа рис. 65 изображен процесс образования трех струй при аннигиляции е+е-
→ q +
Рис. 65: Процесс образования трех струй: а − диаграмма процесса аннигиляции е+е-
→ q +
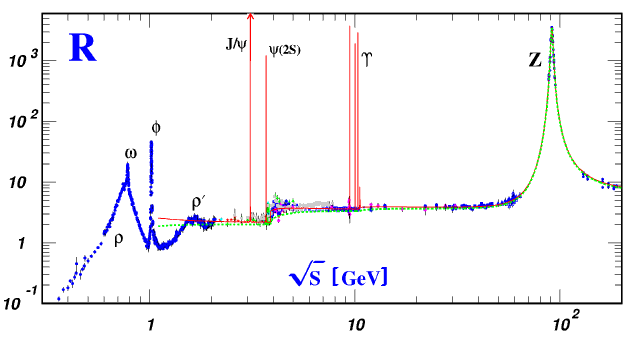
7.4.3 Наличие цвета у кваркаДоказательство существования цвета у кварков было выполнено в экспериментах по изучению процесса е+е- → адроны. На рис. 66 представлено отношение сечения этого процесса к сечению процесса е+е- → лептоны R = σ(е+е- → h)/σ(е+е- → μ+μ-).
Рис. 66: Отношение R в зависимости от энергии, полученное в различных
экспериментах по Сечение процесса е+е- → адроны пропорционально сумме квадратов зарядов кварков, ответственных за образование адронов, ∑(Qi/e)2 , где i − сорт кварка. Сечение процесса е+е- → μ+μ- зависит от энергии (√s) и может быть вычислено по КЭД: σ(е+е- → μ+μ-) = 4πα2/3s ≈ 80 нб/s (s в ГэВ2). Таким образом, R = ∑(Qi/e)2/80 нб/s.
g = 3 − цветовые степени свободы. 7.4.4 Определение потенциала взаимодействия между кварками Потенциал взаимодействия между кварками был определен в экспериментах по
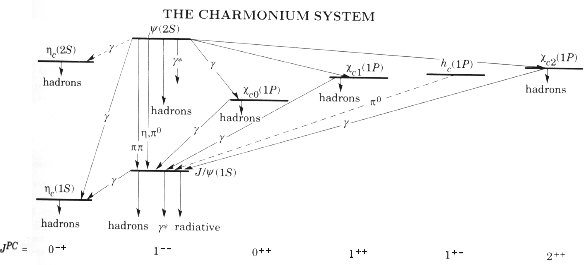
е+е--соударениям с рождением кваркониев. Мезоны, состоящие из с- и
Переходы из одного энергетического состояния в другое сопровождаются испусканием γ-квантов. На опыте измерялись энергии испущенных фотонов в системах кваркониев. Измеренные спектры фотонов были согласованы с вычисленными в предположении о виде потенциала взаимодействия между кварками. Наилучшее согласие между измеренными и вычисленными спектрами получилось в предположении о потенциале взаимодействия между кварками в виде V = − αs/r + æ·г. Особого внимания заслуживает член, описывающий рост потенциала взаимодействия с увеличением расстояния между кварками. Наличие этого члена позволяет объяснить проблему конфайнмента − невылетания кварков из адронов. Литература
|
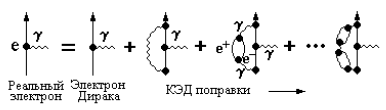
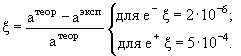
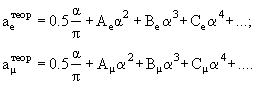
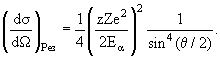
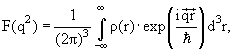
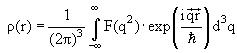 − распределение электрического заряда в ядре.
− распределение электрического заряда в ядре.