Теория Штермера

Основные закономерности движения заряженных частиц в дипольном магнитном поле были исследованы Штермером (Stormer). Полное изложение теории Штермера, включая вывод уравнений и их подробный анализ, приведено в монографии Штермера [1], а также в [10-13]. Отметим, что первые работы Штермера были опубликованы на рубеже XIX-XX веков, т.е. до открытия самих космических лучей, и были направлены на объяснение природы полярных сияний. Ниже представлена краткая сводка основных положений и выводов теории Штермера.

1. Движение заряженной частицы с массой m, скоростью v и зарядом e в магнитном поле описывается уравнением Лоренца

при этом

m₀ - масса покоя частицы. Легко показать, что в стационарном магнитном поле энергия частицы сохраняется, т.е. является первым интегралом движения.
    Т.к. mv² = const ,то специального рассмотрения релятивистских эффектов не требуется.
В цилиндрических координатах (z,ρ,φ)

2. В силу аксиальной симметрии магнитного поля диполя (оно не зависит от координаты φ, Bφ ≡ 0 ) существует еще один интеграл движения

где M − магнитный момент диполя, ось которого направлена вдоль оси z.

3. Штермер ввел новую единицу длины, названную впоследствии его именем,

Здесь Z– заряд частицы в единицах заряда электрона. Переход к штермеровским единицы длины позволяет единообразно анализировать движение частиц различных энергий. С ростом энергии частицы S уменьшается. Круговая орбита с S=1, расположенная в экваториальной плоскости, является устойчивой.

4. Заменив дифференцирование по времени t на дифференцирование по длине пути s с учетом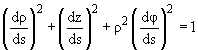 
ds = vdt, запишем 1-й интеграл движения в виде

Уравнение движения меридиональной плоскости, в которой находится частица,

при этом r² = z² + ρ². Здесь γ – момент количества движения частицы относительно оси z, определяемый на бесконечном удалении от диполя. Характер движения частицы вблизи диполя однозначно определяется величиной γ (постоянной Штермера), при этом в зависимости от γ существует определенная конфигурация разрешенных и запрещенных областей движения.

5. Кинетическая энергия движения в меридиональной плоскости характеризуется величиной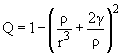

при этом

     

Аналитическое решение полученных уравнений возможно лишь в некоторых частных случаях, например, в экваториальной плоскости диполя.
    Введем угол ω между вектором скорости частицы и направлением восток-запад

    

Поверхность Q = 0, разделяющая разрешенные и запрещенные области движения, определяется соотношением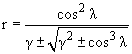

здесь λ – широта, отсчитываемая от экваториальной плоскости диполя. При различных соотношениях между γ и λ получается разное число решений и структура границ областей.

Запрещенные области движения

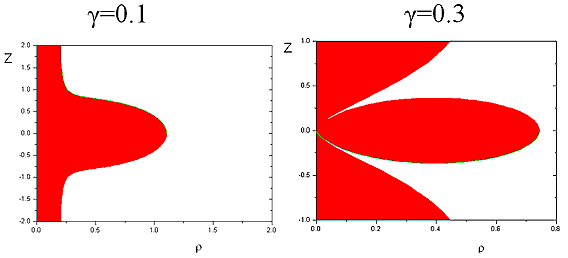
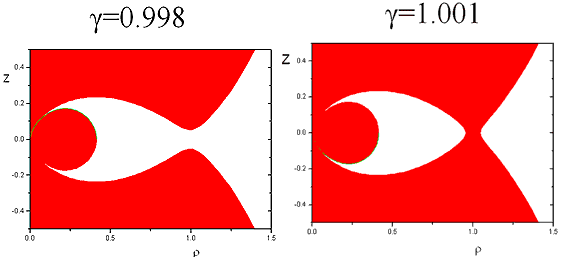
На рисунке показаны меридиональные сечения области вблизи диполя, запрещенные области движения выделены красным цветом. Координаты измеряются в штермеровских единицах длины. Пространственная конфигурация запрещенных областей получается вращением меридиональных сечений вокруг оси z. При γ = 0.3 частица может достичь оси диполя только в точке ρ = 0, z = 0.

Следует обратить внимание на существование внутренней разрешенной области при γ >1, отделенной от всего пространства запрещенной областью. Наличие этой внутренней области обеспечивает устойчивое существование радиационных поясов Земли. При γ = 1 границы внутренней и внешней разрешенной области соприкасаются в точке ρ = 1, z = 0.