1. Энергетические условия двойного бета-распада
В природе существует большое число стабильных четно-четных
ядер-изобар с зарядом, отличающимся на две единицы (A,Z)) и (A,Z±2).
Существование таких ядер обусловлено двумя причинами.
- Силы спаривания между двумя протонами или двумя нейтронами в ядре
приводят к увеличению энергии связи четно-четного ядра по сравнению с
четно-нечетным ядром (A,Z±1).
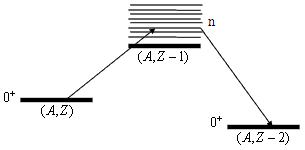
- Промежуточное ядро-изобар (A,Z±1) обладает большей массой, чем ядра (A,Z))
и (A,Z±2), поэтому превращение ядра (A,Z) в более лёгкое ядро (A,Z±2) не
может происходить путём двух последовательных β-распадов (рис. 2)
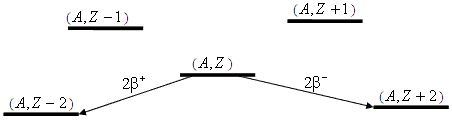
Рис. 2.
Энергетическая диаграмма, поясняющая процесс
двойного β-распада.
В этих случаях превращение ядра (A,Z) в ядро-изобар (A,Z±2)
может происходить с одновременным испусканием двух электронов или двух
позитронов. Впервые на это обратила внимание
М. Гепперт-Майер в
1935 г. [Goeppert-Mayer M., Phys. Rev. 48, 512 (1935)]. Согласно сделанным в
этой работе расчетам период полураспада ядра относительно двойного β-распада
должен составлять 1023
лет.
При двойном β-распаде атомное ядро (A,Z) испускает два
электрона и два антинейтрино или два позитрона и два нейтрино, превращаясь в
ядро с тем же массовым числом A (ядро-изобар) и электрическим зарядом больше или
меньше на две единицы.
2β−-распад: (A,Z) →
(A,Z+2) + 2e− + 2 e, e, |
(2) |
2β+-распад: (A,Z) → (A,Z−2)
+ 2e+ + 2νe. |
(3) |
История двойного β−-распада
- 1871 г. Д. И.
Менделеев открыл периодическую систему химических элементов.
- 1896 г. А. Беккерель открыл
явление радиоактивности.
- 1897 г. Дж. Дж. Томсон открыл
электрон и предложил первую модель атома.
- 1899 г. Э. Резерфорд
открыл, что уран излучает положительно заряженные α-частицы и отрицательно
заряженные β-частицы.
- 1911 г. Э. Резерфорд
предложил модель атома с центральным положительно заряженным ядром.
- 1928 г. П. Дирак получил
релятивистское квантовое уравнение для электрона, названное его именем.
- 1930 г. В. Паули выдвинул
гипотезу о существовании новой элементарной частицы нейтрино для объяснения
спектра электронов β-распада.
- 1932 г. В. Гейзенберг,
Д. Иваненко,
Э. Майорана предложили
протон-нейтронную модель атомного ядра.
- 1935 г. Э. Ферми сформулировал
теорию β-распада и ввел новое понятие − слабое взаимодействие.
- 1935 г. М. Гепперт-Майер
предложила модель двойного β-распада.
- 1937 г. Э. Майорана
предложил модель тождественности нейтрино и антинейтрино.
- 1939 г. В. Фарри
впервые рассмотрел возможность безнейтринного двойного β-распада.
К процессам двойного β-распада относятся также е-захват на
ядре (A,Z) с последующим образованием в конечном состоянии позитрона и двух
нейтрино
e− + (A,Z) → (A,Z−2) + e+
+ 2νe, |
(4) |
а также процесс двойного электронного захвата
(A,Z) + 2e− → (A,Z−2) +
2νe. |
(5) |
В случае (2) двойной β−-распад сопровождается
увеличением заряда ядра на две единицы
(A,Z) → (A,Z+2) и излучением двух электронов и двух электронных антинейтрино 2 e. В других видах
двойного β-распада (3, 4, 5) заряд ядра уменьшается на две единицы (A,Z) → (A,Z−2)
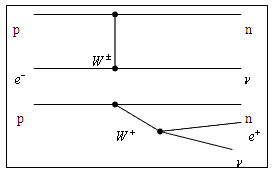
и сопровождается испусканием двух электронных нейтрино 2νe. Диаграммы
Фейнмана двойного β-распада показаны на рис. 3.
e. В других видах
двойного β-распада (3, 4, 5) заряд ядра уменьшается на две единицы (A,Z) → (A,Z−2)
и сопровождается испусканием двух электронных нейтрино 2νe. Диаграммы
Фейнмана двойного β-распада показаны на рис. 3.
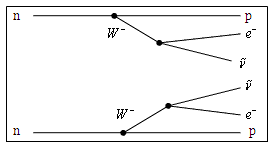 |
(A,Z) → (A,Z+2) + 2e− + 2 e e |
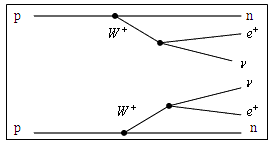 |
(A,Z) → (A,Z−2) + 2e+ + 2νe |
 |
e− + (A,Z) → (A,Z−2) + e+ +
2νe |
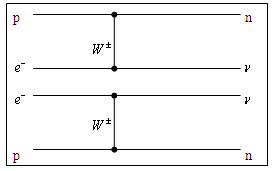 |
(A,Z) + 2e− → (A,Z−2) + 2νe |
| Рис. 3. Диаграммы Фейнмана двойного
β- распада. |
Обычно процессы двойного β-распада сопровождаются
испусканием двух нейтрино 2νe
или двух антинейтрино 2 e, что следует из
закона сохранения лептонного числа Le.
e, что следует из
закона сохранения лептонного числа Le.
Для того, чтобы наблюдался процесс двойного β-распада,
необходимо, чтобы масса начального ядра M(A,Z) была больше масс M(A,Z+2) + 2me
или M(A,Z−2) + 2me, образующихся в результате двойного β-распада.
Двойной β-распад очень редкий процесс. Для того, чтобы его
наблюдать необходимо, чтобы цепочка двух последовательных β-распадов
(A,Z) → (A,Z+1) + e− +
 e → (A,Z+2) + 2e−
+ 2
e → (A,Z+2) + 2e−
+ 2 e,
e,
(A,Z) → (A,Z−1) + e+ + νe → (A,Z−2) + 2e+ + 2νe.
была запрещена по энергии или сильно
подавлена законом сохранения полного момента количества движения J. Двойной β+-распад
может наблюдаться для лёгких изотопов химического элемента, в то время как для
тяжелых изотопов может наблюдаться двойной β−-распад.
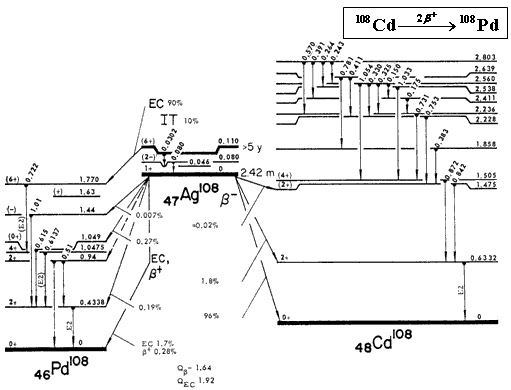
Рис. 4.
Двойной β+-распад изотопа 108Cd.
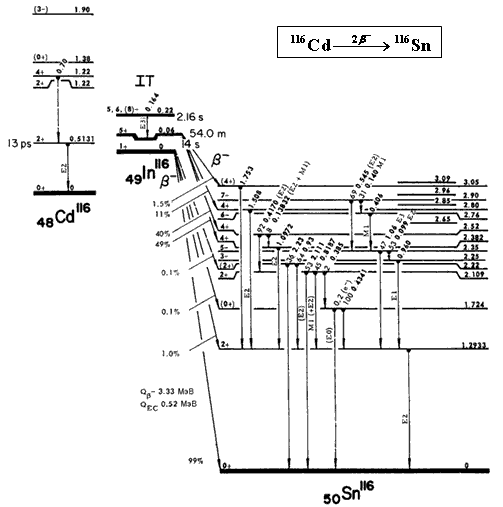
Рис. 5.
Ядра-изобары A = 116 116Cd, 116In,
116Sn.
В качестве примера можно привести два изотопа кадмия 108Cd
и 116Cd. В то время, как для изотопа 116Cd возможен
двойной β−-распад, в изотопе 108Cd возможен двойной β+-распад.
Двойной β−-распад наблюдался в изотопе 116Cd.
Энергия 2β−-распада
116Cd → 116Sn + 2e− + 2 e Q2β = 2.8
МэВ. Усредненное значение измеренного периода полураспада изотопа
116Cd по каналу 2β−2
e Q2β = 2.8
МэВ. Усредненное значение измеренного периода полураспада изотопа
116Cd по каналу 2β−2 e
составляет по данным различных авторов (2.87±0.13)·1019
лет.
e
составляет по данным различных авторов (2.87±0.13)·1019
лет.
Двойной β+-распад
108Cd до сих пор не обнаружен.
Таблица 1
Двойной β−-распад изотопа 116Cd
|
Изотоп
|
Число распадов
|
Период полураспада, лет
|
Ссылка
|
|
116Cd
|
~180
|
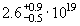
|
H. Ejiri et
al., J. Phys. Soc. of Japan 64 (1995) 339.
|
|
|
176,6
|
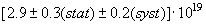
|
R. Arnold et al., Z. Phys. C 72 (1996) 239.
|
|
|
9850
|
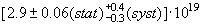
|
F.A.
Danevich et al., Phys. Rev.
C 68 (2003) 035501.
|
|
|
7000
|
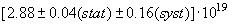
|
A.S.
Barabash, Phys. Part. Nucl. 42 (2011) 613.
|
|
|
34927
|
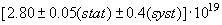
|
D. Poda et al., EPJ Web of Conf. 65 (2014) 01005.
|
|
Среднее значение: (2.87±0.13)·1019
|
|
Энергии двойного β-распада
Энергетическое условие 2β−-распада
Mядра(A,Z) > Mядра(A,Z+2) + 2me
или, переходя к массам атомов,
Mатома(A,Z) > Mатома(A,Z+2).
Энергия, выделяющаяся при 2β−-распаде
Q(2β−) = Mатома(A,Z) − Mатома(A,Z+2).
Энергетическое условие 2β+-распада
Mядра(A,Z) > Mядра(A,Z−2) + 2me
Mатома(A,Z) > Mатома(A,Z−2).
Энергия, выделяющаяся при 2β+-распаде
Q(2β+) = Mатома(A,Z) − Mатома(A,Z−2) − 4me
Энергетическое условие 2e−-захвата
Mядра(A,Z) + 2me > Mядра(A,Z−2),
Mатома(A,Z) > Mатома(A,Z−2).
Энергия, выделяющаяся при 2e−-захвате
Q(2e) = Mатома(A,Z) − Mатома(A,Z−2) −
2ε.
ε − энергия связи орбитального электрона.
Энергетическое условие е-захвата e− + (A,Z) → (A,Z−2)
+ e+ + 2ν
Mядра(A,Z) + me > Mядра(A,Z−2) + me,
Mатома(A,Z) > Mатома(A,Z−2) + 2me.
Энергия, выделяющаяся при е-захвате e− + (A,Z) → (A,Z−2) + e+
+ 2ν
Q(e−,e+2ν) = Mатома(A,Z) − Mатома(A,Z−2)
− 2me − 2ε.
В таблице 2 приводятся энергии, выделяющиеся при различных
типах β-распада и двойного β-распада.
Таблица 2
Типы и энергии β-распада и двойного β-распада
|
Тип распада
|
Энергия распада
|
|
β-распад
|
|
(A,Z) → (A,Z+1) + e−
+  e e
|
Mатома(A,Z) − Mатома(A,Z+1)
|
|
(A,Z) → (A,Z−1) + e+
+ νe
|
Mатома(A,Z) − Mатома(A,Z−1)
− 2me
|
|
(A,Z) + e− → (A,Z−1) + νe
|
Mатома(A,Z) − Mатома(A,Z−1)
|
|
2β-распад
|
|
(A,Z) → (A,Z+2) + 2e− + 2 e e
|
Mатома(A,Z) − Mатома(A,Z+2)
|
|
(A,Z) → (A,Z−2) + 2e+ + 2νe
|
Mатома(A,Z) − Mатома(A,Z−2)
− 4me
|
|
A,Z) + 2e− → (A,Z−2) + 2νe
|
Mатома(A,Z) − Mатома(A,Z−2)
− 2ε
|
|
(A,Z) + e− → (A,Z−2) + e+
+ 2νe
|
Mатома(A,Z) − Mатома(A,Z−2)
− 2me
− 2ε
|
ε − энергия связи орбитального электрона.
Двойной β-распад может происходить не только на основное, но
и на возбужденные состояния конечного ядра. В этом случае он сопровождается
излучением γ-квантов и (или) конверсионных электронов.
Известно ~70 природных радиоизотопов, которые могут
распадаться в результате 2β-распада. Некоторые изотопы, для которых возможен
двойной β−-распад приведены в таблице 3.
Таблица 3
Некоторые четно-четные изотопы, для которых возможен
двойной β−-распад
|
№
|
Распад
(A,Z)→(A,Z+2)
|
A
|
Z
|
Содержание изотопа (A,Z) в естественной смеси
изотопов, %
|
Энергия
2β-распада, кэВ
|
Энергия β-перехода (A,Z)→(A,Z+1),
кэВ
|
|
1
|
Ca → Ti
|
46
|
20
|
0.0033
|
984.5 ± 5.1
|
–1382.6 ± 3.7
|
|
2
|
Ca → Ti
|
48
|
20
|
0.185
|
4271.7 ± 5.4
|
+281 ± 6
|
|
3
|
Zn → Ge
|
70
|
30
|
0.62
|
1001.5 ± 5.2
|
–654.8 ± 1.6
|
|
4
|
Ge → Se
|
76
|
32
|
7.67
|
2045.7 ± 5
|
–922.9 ± 2.7
|
|
5
|
Se → Kr
|
80
|
34
|
49.82
|
135.7 ± 14.5
|
–1870.3 ± 2
|
|
6
|
Se → Kr
|
82
|
34
|
9.19
|
3005 ± 16
|
–88 ± 12
|
|
7
|
Kr → Sr
|
86
|
36
|
17.37
|
1249.1 ± 7.8
|
–526 ± 5
|
|
8
|
Zr → Mo
|
94
|
40
|
2.80
|
1148.4 ±6.5
|
–896.8 ± 2.6
|
|
9
|
Zr → Mo
|
96
|
40
|
17.40
|
3350.2 ± 6.1
|
+163.0 ± 5
|
|
10
|
Mo → Ru
|
98
|
42
|
23.75
|
110.6 ± 8.4
|
–1682 ±5
|
|
11
|
Mo → Ru
|
100
|
42
|
9.62
|
3032.6 ± 8.6
|
–170 ± 6
|
|
12
|
Ru → Pd
|
104
|
44
|
18.5
|
1301 ± 11
|
–1147 ± 7
|
|
13
|
Pd → Cd
|
110
|
46
|
12.7
|
2014 ± 24
|
–879 ± 20
|
|
14
|
Cd → Sn
|
114
|
48
|
28.86
|
540.4 ±7.3
|
–1444 ± 5
|
|
15
|
Cd → Sn
|
116
|
48
|
7.58
|
2808.5 ±7.3
|
–464 ± 8
|
|
16
|
Sn → Te
|
122
|
50
|
4.71
|
358 ± 8
|
–1622.7 ± 3.6
|
|
17
|
Sn → Te
|
124
|
50
|
5.98
|
2278б3 ± 8б8
|
–627 ± 5
|
|
18
|
Te → Xe
|
128
|
52
|
31.79
|
868.9 ± 5.5
|
–1258 ± 5
|
|
19
|
Te → Xe
|
130
|
52
|
34.49
|
2533.1 ± 6.6
|
–451 ± 11
|
|
20
|
Xe → Ba
|
134
|
54
|
10.44
|
843 ± 15
|
–1215 ± 11
|
|
21
|
Xe → Ba
|
136
|
54
|
8.87
|
2481 ± 15
|
–67 ± 11
|
|
22
|
Ce → Nd
|
142
|
58
|
11.07
|
1414 ± 11
|
–745.1 ± 3.5
|
|
23
|
Nd → Sm
|
148
|
60
|
5.71
|
1928 ± 10
|
–536 ± 9
|
|
24
|
Nd → Sm
|
150
|
60
|
5.60
|
3367 ± 11
|
–130 ± 80
|
|
25
|
Sm → Gd
|
154
|
62
|
22.61
|
1250 ± 10
|
–728 ± 5
|
|
26
|
Gd → Dy
|
160
|
64
|
21.75
|
1731 ± 11
|
–102.3 ± 1.4
|
|
27
|
Yb → Hf
|
176
|
70
|
12.23
|
1077 ± 12
|
–109.6 ± 21
|
|
28
|
W → Os
|
186
|
74
|
28.41
|
489 ± 14
|
–587.8 ± 2.6
|
|
29
|
Pt → Hg
|
198
|
78
|
7.23
|
1043 ± 26
|
–330 ± 19
|
|
30
|
Hg → Pb
|
204
|
80
|
6.85
|
414 ± 12
|
–349 ± 5
|
|
31
|
U → Pu
|
238
|
92
|
99.275
|
1146.2 ± 4.6
|
–145.6 ± 1.3
|
Во всех случаях β−-распада кроме двух изотопов
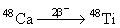 и
и
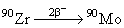 энергии
β-переходов отрицательные. В изотопах 48Ca и
90Zr, несмотря на положительную энергию, β−-распад сильно
подавлен в связи с малой энергией β−-распада и большой разницей
спинов начального и конечного ядер (ΔJ ≥ 5).
энергии
β-переходов отрицательные. В изотопах 48Ca и
90Zr, несмотря на положительную энергию, β−-распад сильно
подавлен в связи с малой энергией β−-распада и большой разницей
спинов начального и конечного ядер (ΔJ ≥ 5).
Прямым доказательством двойного β−-распада
является непосредственная регистрация двух электронов и измерение особенностей
их энергетических спектров. Для регистрации электронов используются различные
детекторы − фотоэмульсии, магнитные спектрометры, сцинтилляционные и кремниевые
детекторы, камеры Вильсона.