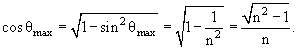Черенковские детекторы

    Принцип работы этого детектора основан на регистрации излучения, открытого П.А. Черенковым в 1934 г. и возникающего при движении заряженной частицы в прозрачной среде со скоростью v большей скорости света u в этой среде. Поскольку u = c/n , где скорость света в вакууме, а n – показатель преломления среды, то условие возникновения черенковского излучения имеет вид v > c/n .
    Черенковское свечение является когерентным излучением диполей, образующихся в результате поляризации среды пролетающей заряженной частицей, и возникает при возвращении этих диполей (поляризованных атомов) в исходное неполяризованное состояние. Если частица двигается медленно, то диполи успевают поворачиваться в её направлении. Поляризация среды при этом симметрична относительно координаты частицы. И излучения отдельных диполей при возвращении в исходное состояние гасят друг друга. При движении частицы со "сверхсветовой" скоростью за счёт запаздывающей реакции диполей они преимущественно ориентируются в направлении движения частицы. Итоговая поляризация оказывается несимметричной относительно местоположения частицы и излучение диполей нескомпенсированным.

Рис. 1. Геометрия черенковского излучения. Угол θ = 900 - α

    Фотоны черенковского излучения испускаются под углом к направлению движения частицы, причем величина этого угла определяется соотношением

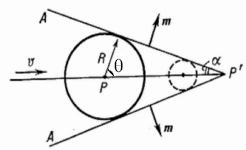
где β = v/c. Это соотношение легко понять на основе принципа Гюйгенса (см. рис. 1). Действительно, огибающая световых волн для частицы, двигающейся со скоростью v > u, представляет собой конус, вершина которого совпадает с положением частицы в данный момент (точка Р' на рисунке), а нормали m к образующим конуса показывают направление распространения черенковского света. На рис. 1 показано, как частица, проходившая в момент времени t через точку Р, породила сферическую электромагнитную волну, которая за время τ распространилась от точки Р на расстояние R = uτ = cτ/n. За то же время частица, двигающаяся со скоростью v > u прошла путь vτ > R и оказалась в точке Р'. Волна от точки Р' ещё не успела распространиться в веществе. Конус AP'A граница области, занятой черенковской электромагнитной волной (её фронт) к моменту t + τ. Угол θ это угол между перпендикуляром, опущенным из точки Р на образующую конуса АР', и линией движения частицы (прямой РР'). Очевидно, косинус этого угла равен отношению длин отрезков R и РР', т.е. cos θ = u/v = 1/βn.

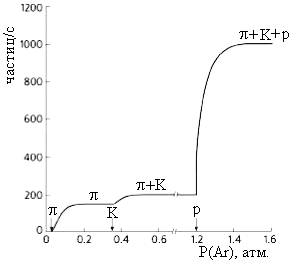
    Энергия частицы, конвертируемая в черенковское излучение, мала по сравнению с её ионизационными потерями. Число фотонов, излучаемых на 1 см пути, в зависимости от среды (радиатора) колеблется от нескольких единиц до нескольких сот.
    Зависимость угла излучения θ от β (1) позволяет, определяя этот угол, найти скорость и энергию частицы. С помощью черенковского детектора можно регистрировать частицы с энергиями вплоть до 100 ГэВ.
    Черенковский детектор позволяет эффективно выделять высокоэнергичные релятивистские частицы на уровне большого фона малоэнергичных частиц.
    В черенковских детекторах используются твердые, жидкие и газообразные радиаторы.

    Различают три типа черенковских детекторов.

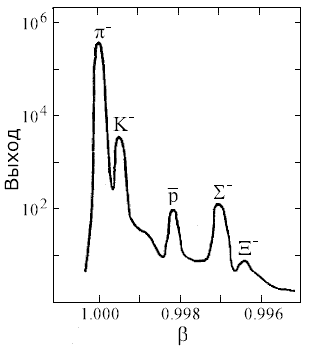
• Пороговые черенковские счетчики.
• Дифференциальные черенковские счетчики.
  • Дифференциальные счетчики с полным внутренним отражением.
  • Дифференциальные счетчики с кольцевой диафрагмой.
• Черенковские детекторы кольцевого изображения или RICH-детекторы (RICH - Ring Imajing CHerenkov).
  • RICH-детекторы с квазифокусировкой (прямой фокусировкой) (Proximity focusing RICH).
  • RICH-детекторы со сферическим зеркалом.
  • RICH-детектор с полным внутренним отражением. DIRC-детекторы (DIRC - Detection of Internally Reflected Cherenkov light).

Пороговые черенковские счетчики

Рис. 2. Схема порогового счетчика

Рис. 3. Зависимость скорости счета частиц в пучке с импульсом 35 ГэВ/с от давления аргона в пороговом черенковском счетчике. Стрелками показаны пороги.

    Пороговые счетчики служат для детектирования частиц со скоростями превышающими порог
β_min = 1/n. Рассмотрим, как можно с помощью пороговых счетчиков различить пионы, каоны и протоны.

Рис. 4. Схема выделения в пучке пионов, каонов и протонов с помощью пороговых счетчиков

В счетчике С₁ радиатор выбран так, что β_π > 1/n₁, а β_K, β_p < 1/n₁.
В счетчике С₂ - β_π, β_K > 1/n₂, а β_p < 1/n₂. Тогда, если

• черенковское свечение в С₁ и С₂ → пион,
• черенковское свечение в С₂ и отсутствует в С₁ → каон,
• черенковское свечение в отсутствует в С₂ и  С₁ → протон.

Дифференциальные черенковские счетчики

Рис. 5. Схема дифференциального черенковского счетчика.

    Дифференциальные черенковские счетчики регистрируют частицы в определенном интервале скоростей. Они бывают двух типов.
    Минимальная скорость, при которой в радиаторе с показателем преломления n возникает черенковское излучение β_min = 1/n. При этом фотоны летят вперед (θ_min = 0) и попадают в воздушный световод (рис. 4). При увеличении скорости черенковский угол увеличивается пока не не наступит условие полного внутреннего отражения:

sin θ_max = 1/n.

(2)

Из (1) и (2) получим

Таким образом, в ФЭУ будут попадать только фотоны в диапазоне скоростей β_min < β < β_max.

Рис. 6. Схема дифференциального черенковского счетчика с кольцевой диафрагмой (DISC detector).

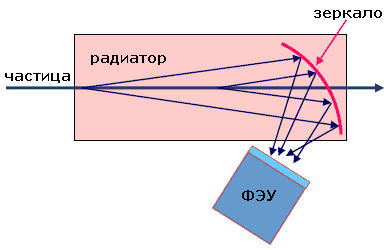
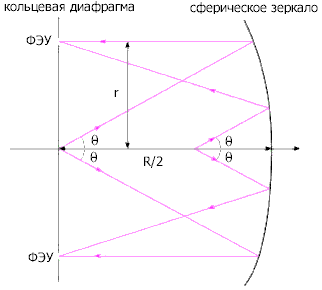
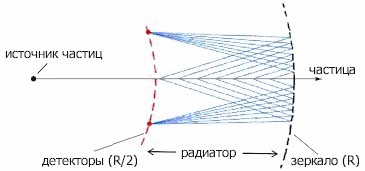
    Схема другого метода реализации дифференциального счетчика показана на рис. 6. Черенковские фотоны отраженные сферическим зеркалом радиуса R собираются в его фокальной плоскости (R/2), где устанавливается кольцевая диафрагма радиуса r. Фотоумножителями регистрируются только те фотоны, которые попадают в щель диафрагмы

(3)

Таким образом, учитывая связь между скоростью β и черенковским углом θ (1), удается выделить частицы в узком интервале скоростей. При использовании коррекции хроматической аберрации удается достичь разрешение по скоростям Δβ/β ≈ 10^-7. Такие счетчики позволяют отделить пионы от каонов при энергии до нескольких сот ГэВ. 

Рис. 7. Пример разделения частиц с помощью дифференциального счетчика.

На встречных пучках дифференциальные счетчики не применяются, т.к. там необходимо детектировать частицы в 4π геометрии. Там применяются RICH-детекторы.

Черенковские детекторы кольцевого изображения (RICH-детекторы)

RICH-детекторы с квазифокусировкой

Рис. 8. Схема RICH-детектора с квазифокусировкой.

Рис. 9. Схема RICH-детектора с многослойным радиатором.

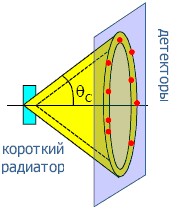
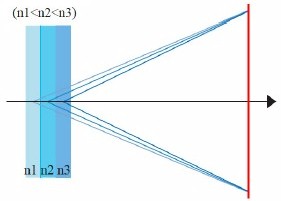
    В RICH-детекторах с квазифокусировкой (прямой фокусировкой) радиатор обычно выбирается тонким (~1 см) с большим показателем преломления. Фотонные детекторы обычно располагается на расстоянии 5-10 см (рис. 8), где формируется кольцо. Для того, чтобы улучшить идентификацию частиц, например пионов и каонов, надо увеличивать число фотонов и улучшать угловое разрешение. Для того, чтобы увеличить выход черенковских фотонов, надо увеличивать толщину радиатора. Однако это приводит к увеличению неопределенности в определении точки их эмиссии, что ведет к ухудшению точности определения черенковского угла. Проблему можно решить, используя многослойный радиатор с изменяющимся по слоям показателем преломления (рис. 9).

Рис. 10. Схема черенковского RICH-детектора, установленного на AMS-02.

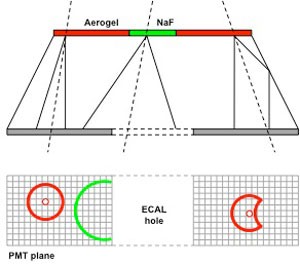
    Как пример RICH-детекторах с квазифокусировкой рассмотрим черенковский детектор детекторного комплекса AMS-02. (Запуск детекторного комплекса AMS-02 (Alpha Magnetic Spectrometer) был произведён 16 мая 2011 года, а 19 мая он был установлен на МКС.)Детектор состоит из радиатора, в центральной части которого слой NaF (показатель преломления – n = 1.335), окруженный слоем аэрогеля (n = 1.03–1.05). Черенковское излучение регистрируется несколькими тысячами миниатюрных фотонных детекторов. В центре области детекторов – отверстие, которое позволяет регистрируемым в AMS частицам без помех пролететь в электромагнитный калориметр. Черенковский детектор окружен коническим зеркалом. Черенковский конус регистрируется фотонными детекторами в виде эллипса. За счет большего показателя преломления NaF раствор конуса большой и часть фотонов попадает в чувствительную область, несмотря на наличие центрального отверстия. Фотоны отражаясь от зеркала также регистрируются. С помощью алгоритма распознавания образов по зарегистрированным проекциям черенковских конусов можно реконструировать скорости частиц и углы их влета. По ширине линий можно оценить их заряд.

RICH-детекторы со сферическим зеркалом

Рис. 11. Схема RICH-детектора со сферическим зеркалом.

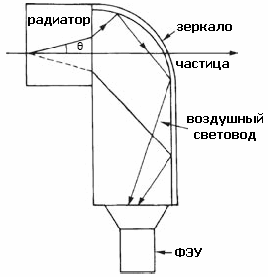
    Если в качестве радиатора используется газ, для того чтобы излучалось достаточное количество фотонов, толщина радиатора должна быть довольно большой. В этом случае для фокусировки используются сферические или параболические зеркала.
    В таком детекторе радиатор находится между двумя сферическими поверхностями (рис. 11). Наружная –  сферическое зеркало радиуса R. Источник частиц находится в центре сферы. На внутренней сфере радиуса R/2 устанавливаются фотодетекторы. Отраженный от зеркала черенковское излучение фокусируется на внутреннюю сферу, образуя кольцо радиусом

r = R/2 × tg(θ),

Рис. 12. Схема черенковского детектора в LHCb.

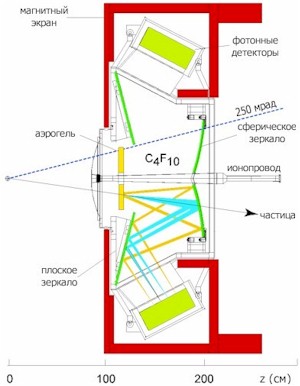
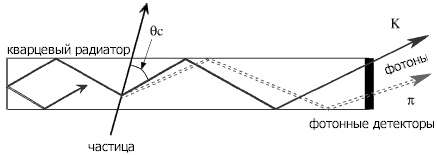
который измеряется фотодетекторами.

    На рис. 12 показана схема черенковского детектора в LHCb. В этом детекторе используются два радиатора: твердый (аэрогель) и газовый (C₄F₁₀). Для того чтобы уменьшить область, в которой частицы могут взаимодействовать с материалом фотодетекторов, устанавливают дополнительные плоские зеркала. Использование дополнительных плоских зеркал позволило уменьшить "мертвую зону". Частицы, рождающихся при столкновениях в LHCb летят сквозь сферические зеркала. Чтобы уменьшить рассеяние, в RICH-1 используется специальные зеркала, изготовленные пластика, армированного  углеродным волокном (углепластика). 

DIRC-детекторы

    В этом варианте RICH-детектора оптический материал радиатора одновременно используется и как черенковский радиатор, и как светопровод. Радиатор (например кварц) имеет прямоугольную форму. За счет этого, фотоны черенковского излучения, испущенные под углом θ, распространяются вдоль пластины за счет полного внутреннего отражения с сохранением этого угла до самого торца пластины, где расположен позиционно-чувствительный фотоприёмник. Причем это происходит вне траектории частицы. Из-за разницы в черенковских углах частиц (на рис.13 пионов и каонов) разнятся длины и соответственно времена прохождения света. В результате событие отображается в трех измерения – двух пространственных и временном. Это позволяет улучшить точность определения черенковского угла, провести коррекцию хроматической аберрации.

Рис. 11. Схема RICH-детектор с полным внутренним отражением.

    Реализация RICH-детектора без зеркал.

Литература

• Википедия. RICH-детекторы
• Ю.П. Добрецов. Методы идентификации частиц в экспериментальной физике высоких энергий
• Ю. Н. Харжеев. Использование аэрогеля диоксида кремния в черенковских счетчиках. ЭЧАЯ 2008. Т. 39. ВЫП. 1
• Christian Joram. Particle Identification Techniques in High Energy Physics
• Christian Lippmann. Particle identification
• Roger Forty. Particle Identification
• H.-C. Schultz-Coulon, J. Stachel. The Physics of Particle Detectors Lecture11. Particle ID. Distinguishing Particles
• Peter Križan. Advances in particle-identification concepts
• Fritz DeJongh. Cerenkov Detectors