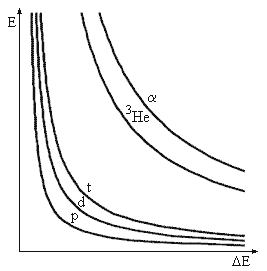
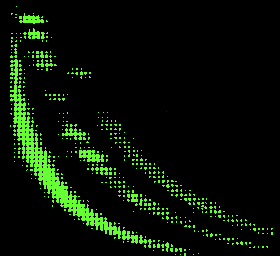
Идентификация заряженных частиц низких и средних энергий

    В экспериментах по исследованию структуры ядер и механизмов ядерных реакций почти всегда необходимо не только измерять энергию частиц, но и идентифицировать их. По мере роста энергии и массы бомбардирующих частиц растет число открывающихся каналов реакций, а соответственно и набор  образующихся ядер. Проблема надежной идентификации продуктов реакций особенно остро стоит в физике тяжелых ионов. Рассмотрим различные методы идентификации частиц.

Идентификация на основе измерений удельных потерь энергии и полной энергии (ΔE-E-метод)

    Этот метод является основным при исследовании реакций с легкими ионами (¹Н, ²Н, ³Н, ³Нe, ⁴Нe). В нем используется телескоп детекторов, состоящий из тонкого прострельного детектора ΔE и детектора полного поглощения энергии E. (В качестве ΔE-детектора используют тонкие кремниевые детекторы, а также ионизационные камеры и пропорциональные счетчики, в качестве детектора полного поглощения - кремниевые детекторы или детекторы из сверхчистого германия HpGe) Потери энергии в ΔE детекторе

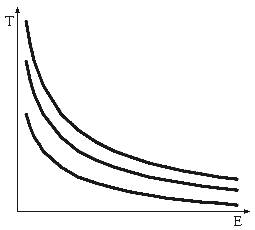
где dE/dx - удельные потери энергии в прострельном детекторе, d - его толщина. Формулу для удельных потерь Бете-Блоха в нерелятивистском случае, пренебрегая слабо зависящим от энергии логарифмическим членом, можно записать в виде

dE/dx kAZ2/E,

(2)

Рис. 1. ΔE-E распределение.

Рис. 2. Проекция сечения E = const. на ось ΔE.

где k - коэффициент, не зависящий от массового числа A и заряда Z частицы. AZ² носит название параметра идентификации. Величина сигнала ΔE-канала пропорциональна kAZ²/E, Е-канала - E - kAZ²/E. На плоскости ΔE-E распределение отображается семейством гипербол, каждая из которых соответствует частице (нуклиду) с определенным значением массового числа  и заряда (см. рис.1). Толщина прострельного детектора определяет нижнюю и верхнюю границы измеряемого энергетического диапазона для данного нуклида. Если энергия мала, то частица оставит практически всю энергию в прострельном детекторе, а сигнал от детектора полного поглощения будет мал и "утонет" в шумах. Если энергия велика, наоборот. В экспериментальных ΔE-E распределениях гиперболы размыты. На рис. 2 показано как приблизительно выглядят проекции на ось ΔE сечения по энергии в Е-канале. Ширина распределений определяется не только шумами детекторов и электроники, но и другими факторами, среди которых следующие:

• Статистические флуктуации потерь в тонких детекторах.
• Неоднородность толщины ΔE-детектора, которая приводит к разбросу потерь энергии в нем и в Е детекторе.
• Разброс пробегов и потери энергии в мертвых слоях детекторов.
• Флуктуации величины заряда. Средний заряд иона Z_эф при прохождении ΔE  детектора совпадает с атомным номером Z только у самых легких ионов. По мере роста Z и/или уменьшения энергии различие между Z и Z_эф возрастает. Для тяжелых ионов влияние этого эффекта на разрешение может быть заметно больше, чем влияние статистических флуктуаций потерь.

    Чем тяжелее ионы, тем указанные факторы сильнее ограничивают возможности ΔE-E-метода. Относительное изменение параметра идентификации для двух соседних изотопов данного элемента
ΔA/A у протонов 1, у  ²⁰Ne - 0.05, у изотопов аргона - 0.025,  а у изотопов ксенона - <00.1. Кроме того,  для идентификации тяжелых ионов нужны очень тонкие прострельные детекторы. Хорошие же твердотельные ΔE-детекторы с толщиной менее 10 мкм редкость, т.к. трудно добиться высокой однородности их толщины. Для идентификации тяжелых ионов в качестве ΔE-детектора используются газовые детекторы (ионизационные камеры и пропорциональные счетчики). В них необходимую толщину можно оперативно установить, изменив давление газа. Их площадь может быть сделана заметно большей, чем у полупроводниковых детекторов. Кроме того, они радиационно устойчивы. Недостатком газовых детекторов являются заметно худшие по сравнению с твердотельными детекторами временные характеристики.
    При увеличении атомного номера может возникнуть ситуация, когда нейтроноизбыточные изотопы элемента Z  и нейтронодефицитные изотопы элемента Z+1 будут иметь близкие параметры идентификации.
    Все указанные факторы ограничивают применимость ΔE-E-метода для ионов с массовыми числами A более ~20. Разрешение по Z в два раза лучше, чем разрешение по A.

Рис. 3. Блок-схема электроники для идентификации частиц ΔE-E-методом.

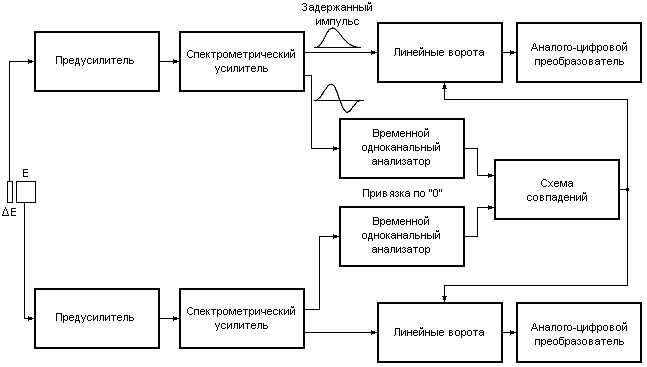
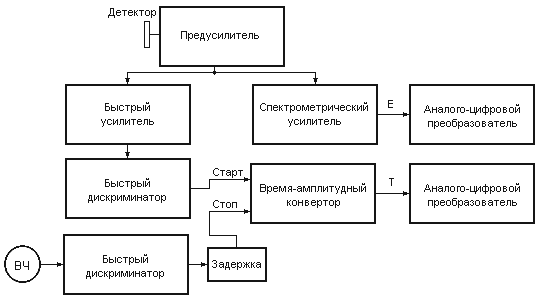
На рис. 3. показана примерная блок-схема электроники для идентификации частиц ΔE-E-методом.

Рис. 4. Экран монитора с гиперболами однозарядных ионов. Нижняя гипербола – протоны, средняя – дейтроны, верхняя – тритоны. Ось x – ΔE, ось y – E.

ΔE- и E-каналы идентичны. С одного из выходов спектрометрического усилителя снимается биполярный сигнал, который поступает на временной одноканальный анализатор. Он служит для выделения нужного амплитудного (энергетического) диапазона и для получения временной метки. В данном случае она получается с помощью метода привязки по нулю биполярного сигнала. Сигналы с временных одноканальных анализаторов поступают на схему совпадений, которая управляет линейными воротами. Таким образом, линейные ворота пропускают только сигналы, которые находятся в интересующем энергетическом диапазоне и совпадают в пределах разрешающего времени. 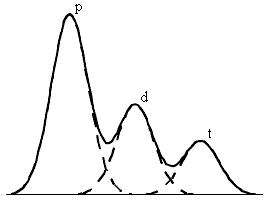Сигналы с линейных ворот поступают в АЦП и далее в систему двумерного анализа. Теперь можно выделить области двумерного спектра, соответствующие определенным частицам, и спроецировать эту область на ось Е, получив, таким образом, амплитудные (энергетические) спектры для отдельных частиц. В полученных таким образом спектрах зависимость между энергией частицы Е и номером канала n нелинейная, так как в Е-канале регистрируется не вся энергия Е, а только оставшаяся после прохождения ΔE-детектора и n пропорциональна этой энергии,

Коррекцию потерь в ΔE-детекторе несложно сделать, воспользовавшись таблицами удельных потерь.
    Для увеличения диапазона энергий и регистрируемых частиц, например, если желательно одновременно снимать спектры ¹Н, ²Н, ³Н, ³Нe, ⁴Нe в широком энергетическом диапазоне, можно использовать телескоп из трех детекторов тонкого ΔE₁, более толстого ΔE₂ и Е. Тогда для низких энергий и/или более тяжелых частиц в качестве прострельного детектора будет служить детектор ΔE₁, а полное поглощение будет происходить в детекторах ΔE + Е. Для более высоких энергий и/или более легких частиц в качестве прострельного - ΔE₁ + ΔE₂, а полное поглощение будет происходить в детекторе Е.

Идентификация на основе измерений энергии и времени пролета (E-t-метод)

Рис. 5. Зависимость времени пролета от энергии частиц с разными массами.

    Метод времени пролета является основным для измерения энергетических распределений нейтронов. Детектор используется в этом случае для того, чтобы получить информацию только о времени попадания в него нейтрона. В случае заряженных частиц нет проблем получения с детектора также и энергетической информации. Для нерелятивистских частиц время пролета связано с кинетической энергией соотношением

(4)

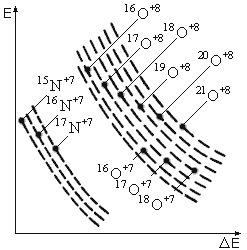
где t_f - время пролета в наносекундах, d - пролетная база в метрах, A - массовое число частицы в атомных единицах массы, E - кинетическая энергия частицы в МэВ. Таким образом, одновременно измеряя энергию и время пролета можно провести идентификацию частиц по массам, измеряя двумерные распределения энергия - время пролета. Ионы, имеющие близкие массы, но разные заряды, естественно различаться не будут.
    Разрешение по массам E-t-метода при использовании полупроводникового детектора практически полностью определяется временным разрешением

Представим (5) в следующем виде

При гауссовом распределении и ΔА = 0.59 а.е.м. 95% частиц будут зарегистрированы в правильном массовом интервале. В табл. 1 приведены вычисленные по формуле (6) разрешения по массам для различных энергий и массовых чисел для установки с пролетной базой 1 м и временным разрешением 1 нс.

Таблица 1. Разрешение по массам для частиц различных энергий и масс.

    На рис. 6 показана блок-схема электроники, которая может быть использована для идентификации по E-t-методу.

Рис. 6. Упрощенная блок-схема электроники для одновременного измерения энергии и времени пролета.

    Импульсы детектора поступают в зарядочувствительный предусилитель. С зарядочувствительного предусилителя сигналы поступают как на быстрый, так и на спектрометрический усилитель. Сигналы быстрого усилителя поступают на быстрый дискриминатор, который служит для временной привязки. Стандартные таймирующие сигналы от быстрого дискриминатора поступают на стартовый вход ВАКа. На стоповый вход поступают сигналы от другого быстрого дискриминатора, который формирует таймирующие сигналы, используя периодические модуляции пучка (например, ВЧ циклотрона). Импульсы ВАКа, амплитуда которых пропорциональна времени пролета поступают в АЦП. В другой АЦП поступают сигналы со спектрометрического усилителя, амплитуда которых пропорциональна энергии. Сигналы АЦП поступают в систему двумерного анализа, как и в ΔE-E-методе.
    Разрешение по времени и, соответствено, по массе можно улучшить по сравнению с рассмотренным вариантом, если для хронирования вместо ВЧ использовать поставленную на пути частицы тонкую пленку. При прохождении частиц через эту пленку из нее будут выбиваться вторичные электроны, регистрируемые микроканальной пластиной. Сигналы от микроканальной пластины поступают на зарядочувствительный предусилитель. С предусилителя - на быстрый усилитель + быстрый дискриминатор. В этом случае таймирующие сигналы микроканальной пластины поступают на стартовый вход ВАКа, а от детектора частиц - на стоповый.
    Комбинация E-t и ΔE-E-методов позволяет продвинуться в разделении нуклидов по Z до ~28, а по А до ~60.

Идентификация с помощью магнитного анализа

    Из уравнения магнитного анализа

Рис. 7. Схема магнитного анализа в сочетании с E-E-методом.

Рис. 8. E-E распределение после магнитного анализа

где А - массовое число иона, q - его заряд, Е - кинетическая энергия иона, В - напряженность магнитного поля, R - радиус кривизны иона в магнитном поле,  следует, что фиксируя B и R в магнитном спектрометре и одновременно измеряя кинетическую энергию E, можно определять отношение массового числа к квадрату ионного заряда, т.е. производить идентификацию.
    Недостатком такой системы является ее низкая эффективность. В детектор попадают частицы из очень узкого энергетического диапазона. Для того чтобы снять весь спектр, необходимо неоднократно менять   напряженность магнитного поля. Этот недостаток можно частично преодолеть, поставив в фокальную плоскость позиционно-чувствительные детекторы. Другой недостаток заключается в том, что не происходит разделения изотопов с близкими значениями A/q², например изобар соседних элементов, находящихся в одинаковых зарядовых состояниях.
    Преодолеть этот недостаток позволяет объединение магнитного анализа с ΔE-E-методом. Вырождение по изобарам с одинаковыми ионными состояниями здесь снимается, т.к. величина удельной ионизации зависит не от ионного заряда, а от среднего заряда иона Z_эф.

Объединение методов идентификации

    Для надежной идентификации нуклидов в широком диапазоне массовых чисел А и атомных номеров Z созданы установки, в которых используются все три метода идентификации. Запишем уравнения идентификации в следующем виде

Массовое число А входит во все три уравнения. В то же время атомный номер Z прямо не входит ни в одно из них. Однако, используя данные по удельным потерям можно рассчитать потери энергии в тонком  ΔE-детекторе, получив еще одно уравнение идентификации [1]

Использование кривой Брегга для идентификации частиц

    Кривая зависимости удельных ионизационных потерь энергии от пробега (кривая Брегга) - "визитная карточка" для заряженной частицы. В начале 80-х было предложено использовать ее для идентификации частиц [4]. Для реализации этой идеи были созданы соответствующие ионизационные камеры.
    Измерения кривой Брегга в газовой среде позволяют получить следующие характеристики частицы: ее энергию Е, пробег R, удельные потери dE/dx и амплитуду брегговского пика A_BP (удельные потери в максимуме кривой Брегга). Существует два способа идентификации частиц, основанных на измерениях характеристик кривой Брегга. В первом траектория частиц перпендикулярна электродам ионизационной камеры, во втором - параллельна.

Идентификация частиц с помощью ионизационной камеры с электродами, перпендикулярными траектории частицы
Bragg Curve Spectroscopy (BCS)

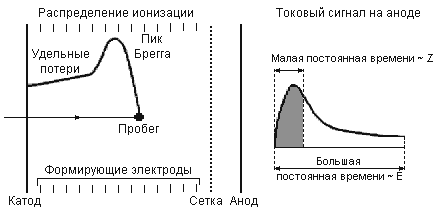Рис. 9. Схемы ионизационной камеры и BCS-метода.

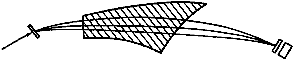
    На рис. 9 показана схема ионизационной камеры с электродами перпендикулярными траектории частицы. Расстояние между катодом и сеткой Фриша больше, чем максимальный пробег идентифицируемых частиц, расстояние между сеткой Фриша и анодом меньше, чем минимальный пробег идентифицируемых частиц. Детектируемые частицы через тонкое входное окно попадают в камеру, заполненную газом. (Входное окно - тонкая пластиковая пленка, расположенная максимально близко к катоду, катод в этом случае представляет собой сетку. Катод или часть его можно сделать из металлизированной пленки, тогда одновременно он будет служить и входным окном.) Заряженная частица вызывает ионизацию газа. Распределение электронной плотности вдоль трека частицы соответствует кривой Брегга.  Возникающие в результате ионизации электроны с постоянной скоростью движутся в однородном электрическом поле по направлению к сетке Фриша. (Однородность электрического поля обеспечивается формирующими электродами, напряжение на которые подается от делителя напряжения.) Сетка Фриша экранирует анод от зарядов, которые находятся между ней и катодом. (Для того чтобы не допустить сбора электронов на сетке Фриша, электрическое поле между сеткой и анодом должно быть больше, чем между катодом и сеткой.) Таким образом, собираемый на аноде заряд определяется только электронами, движущимися между сеткой Фриша и анодом. Это означает, что форма токового сигнала на аноде - зеркальное отражение кривой Брегга. Для извлечения полезной информации, содержащейся в токовом сигнале с анода, применяется как аналоговая, так и цифровая обработка сигналов.

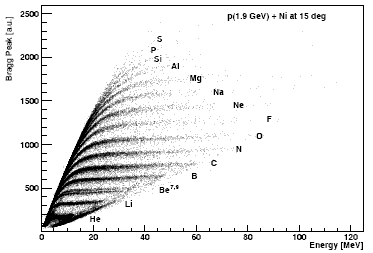Рис. 10. Двумерное распределение Е-ABP.

   При аналоговой обработке сигнал с анода поступает на зарядочувствительный предусилитель. С предусилителя сигнал подается на два усилителя. Один из них имеет большую постоянную времени (~6-8 мкс) так что происходит интегрирование всего сигнала и амплитуда выходного сигнала пропорциональна энергии частицы. Другой усилитель имеет заметно меньшую постоянную времени, приблизительно равную времени пролета электронов от брегговского пика между сеткой Фриша и анодом (~0.1-0.5 мкс), его амплитуда пропорциональна амплитуде токового сигнала A_BP и, соответственно, заряду иона. Ионы, с разными энергиями, но с одинаковыми зарядами, испытывают приблизительно одинаковые удельные потери в области брегговского пика. На рис. 10 показано распределение Е-A_BP. Область A_BP = const определяется расстоянием между сеткой Фриша и анодом и соответственно связанной с ним постоянной времени формирующих цепей усилителя. Когда пробег иона меньше этого расстояния, в обоих усилителях интегрируется весь сигнал и идентификация оказывается невозможной.

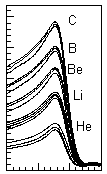Рис. 11. Эталонные сигналы.

    При цифровой обработке сигнала используются быстрые параллельные АЦП, позволяющие зафиксировать форму сигнала и провести идентификацию не только по Z, но и по массовому числу А, по крайней мере, для легких элементов. Это можно сделать, например, используя эталонные сигналы, полученные для различных изотопов, и сравнивая форму измеренного сигнала с эталонными (см. рис. 11).

Идентификация частиц с помощью ионизационной камеры с электродами, параллельными траектории частицы
Range Sensitive Telescope (RST) Detector

    На рис. 12 показана схема ионизационной камеры с электродами, параллельными траектории частицы.

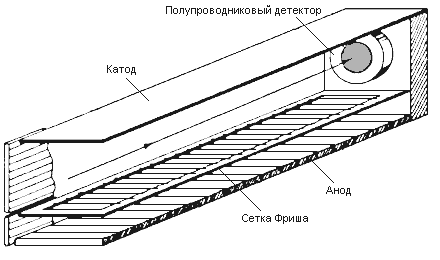Рис. 12. Чувствительный к пробегу телескоп детекторов.

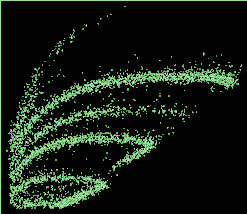Рис. 13. Двумерное распределение  V1(V2). Видны локусы 6Li, 9Be, 10B, 12C, 14N и 16O.

     В случае резистивного анода сигналы V₁ и V₂ снимаются с его противоположных концов. Если пробег частицы R больше длины ионизационной камеры L, то она работает как ΔE-детектор. Суммарный сигнал пропорционален энергетическим потерям в камере (ΔE = k[V₁ + V₂]). Если R < L система работает в другом режиме. Заряд, который попадает на его сегмент dx, пропорционален величине ионизационных потерь.  Вклад в сигналы V₁ и V₂ от анодного интервала
(x, x + dx)

,

(9)

,

(10)

где энергия частицы в точке x

.

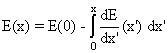(11)

Здесь E(0) - энергия частицы в начале пролета через камеру. После интегрирования (9) и (10) получим

,

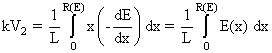(12)

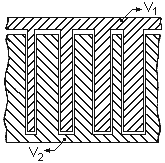Рис. 14. Секционированный анод.

Сигналы V₁ и V₂ используются для идентификации. На рис. 13 показано двумерное распределение  V₁(V₂).

    Вместо резистивного анода можно использовать анод состоящий из двух частей (см. рис. 14). Ширины ламелей можно подобрать такими, что кривые V₁(V₂) будут иметь линейные участки в широком энергетическом диапазоне и довольно большом диапазоне Z. На рис. 15-16 показаны результаты расчетов V₁(V₂) с анодом, оптимизированым для ²⁴Mg, и с резистивным анодом.  Видно, что линейность сохраняется в довольно широком диапазоне Z.

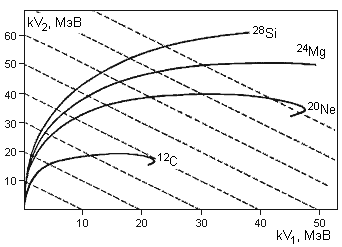Рис. 15. Рассчитанные кривые kV1(kV2) для резистивного анода. Загибы у 20Ne и 12С возникают при энергиях, когда пробег ионов в камере больше ее длины.

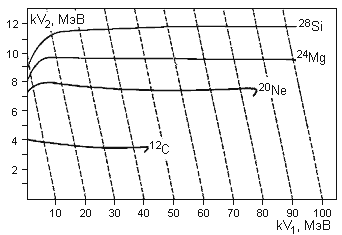Рис. 16. Рассчитанные кривые kV1(kV2) для анода состоящего из двух частей с оптимизированными для 24Mg ширинами ламелей.

Литература

1. В.В. Волков. Ядерные реакции глубоконеупругих передач. М:, Энергоиздат, 1982.
2. А.А. Курашов Идентификация ионизирующих излучений средних и низких энергий. М:, Атомиздат, 1979.
3. О.Ф. Немец, К.О. Теренецкий Ядерные реакции. Киев,  Вища школа, 1977.
4. C.R.Gruhn, et al. Nucl. Instr. and Meth., 196 (1982) 33.
5. G.M. Santos, J.C. Acquadro, R.M. Anjos et al. A Bragg detector built for AMS purposes. Revista de Fisica Aplicada e Instrumentacao, vol. 13, no. 3 (1998)
6. G. D'Erasmo, D. Fabris, F. Gramegna et al. Progress report on heavy ion identification by Bragg curve spectroscopy at Legnardo XTU Tandem Laboratory. Prep. INFN/BE-82/4
7. M. Karlsson. Measurment of two-body photodisintegration of ³H and ³He at photon energies 12 - 32 MeV.
8. M. Hagiwara, M. Baba, T. Oishi et al. Measurement of double differential cross sections for fragment-production induced by tens of MeV particles.
9. PISA Collaboration. The PISA experiment: Spallation products identified by Bragg curve spectroscopy.
10. M.N. Andronenko and W. Neubert. Application of Pulse Shape Analysis to Isotope Separation in Bragg Curve Spectroscopy.
11. Z. Sosin, T. Kozik, S. Micek and K. Grotowsky. Range Sensitive Telescope Detector. Nucl. Instr. and Meth., 224 (1984) 454-460.

[Эксперимент]