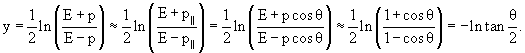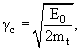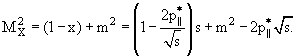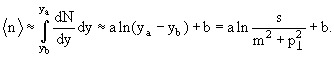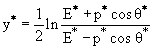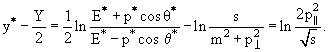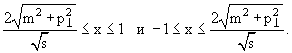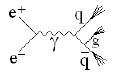7 Процессы взаимодействия при столкновениях частиц высоких энергий
7.1 Способы изучения разных типов взаимодействий
При анализе процессов соударения используют эксклюзивный, инклюзивный и
эвентуальный методы. Эксклюзивный метод применяется, если существует полная
информация обо всех продуктах реакции. Этот метод имеет ограничения, поскольку с
ростом энергии соударяющихся частиц растет число вторичных частиц и не все
характеристики вторичных частиц могут быть измерены. Поэтому при высоких энергиях применяется инклюзивный метод анализа, который позволяет
по характеристике одной из вторичных частиц определить свойства взаимодействия.
Инклюзивный метод состоит в сведении многочастичной реакции к двухчастичной, в
которой в результате взаимодействия рассматриваются характеристики только одной
из рожденных во взаимодействии вторичных частиц, а характеристики всех остальных
частиц суммируются.
Полное поперечное сечение процесса столкновения складывается из упругого,
неупругого и квазиупругого процессов: σtot = σel + σinel + σqel.
Упругий процесс a + b → a + b допускает использование эксклюзивного
метода.
Неупругий и квазиупругий процессы анализируются с использованием как
эксклюзивного, так и инклюзивного методов.
В реакции a + b → a + b + c1 + c2 + ... +
cn применяется эксклюзивный метод,
если характеристики всех вторичных частиц измерены. Ограничения в эксклюзивном
методе связаны в первую очередь с рождением нейтральных частиц среди продуктов
реакции. В этом случае характеристики нейтральных частиц часто бывают недоступны
для измерения. Далее с ростом энергии соударяющихся частиц может быть потеряна
информация и о характеристиках заряженных частиц. В таком случае реализуется
инклюзивный метод, в котором процесс взаимодействия может быть представлен в
виде двухчастичной реакции: a + b → ci + X (i = 1÷n). В систему X входят все
вторичные частицы, включая сохранившиеся после соударения первичные частицы.
Информация о событии может быть получена в эвентуальном методе или, как его теперь называют, event-by-event-анализ. Смысл
этого метода состоит в том, что в реакции а + b → а + b + X определяются
особенности X-системы: значение коэффициента неупругости для такой реакции,
множественность вторичных частиц, особенности угловых характеристик Х-системы и
др. В этом случае в событиях с данной множественностью или с данным
коэффициентом неупругости изучаются импульсные спектры вторичных частиц и другие
их характеристики. Эвентуальный метод содержит больше информации о процессе
соударения, чем инклюзивный, и не имеет ограничений при возрастании энергии
сталкивающихся частиц.
7.2 Множественное рождение частиц
Множественность вторичных частиц − одна из основных эвентуальных
характеристик процесса взаимодействия. Процесс множественного рождения, играющий
определяющую роль при столкновении частиц высоких энергий, является
совокупностью многих различных механизмов взаимодействий. Эксперименты показали,
что множественное рождение частиц происходит при столкновении любых известных в
настоящее время частиц, если их энергия превышает пороговую, составляющую
несколько гигаэлектрон-вольт. Поэтому, если первоначально множественное рождение
изучалось главным образом в адрон-адронных соударениях, то сейчас получены
экспериментальные данные о множественном рождении при столкновениях е±р, μ±p, γp, νp,
 p и в процессах е+е--аннигиляции. Таким образом, множественное рождение
частиц - это универсальный процесс, происходящий в любых типах взаимодействий: сильных, электромагнитных и слабых. p и в процессах е+е--аннигиляции. Таким образом, множественное рождение
частиц - это универсальный процесс, происходящий в любых типах взаимодействий: сильных, электромагнитных и слабых.
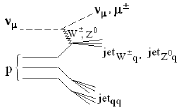
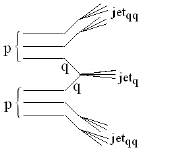
Универсальным процессом для всех типов взаимодействий является множественное
рождение частиц. На рис. 70 показаны основные диаграммы Фейнмана,
иллюстрирующие, что при любом типе взаимодействия множественное рождение частиц
происходит в результате процесса адронизации кварков в кварковых и глюонных
струях. Процесс адронизации находится в стадии изучения. Первоначально
предполагалось, что множественное рождение частиц может происходить только в
сильных взаимодействиях. Поэтому основные характеристики этого процесса были
изучены во взаимодействиях адронов друг с другом и с атомными ядрами. Были
изучены такие характеристики как множественность, импульсные и угловые
распределения. Изучение импульсных характеристик и особенно распределений по
поперечным импульсам привело к открытию новых закономерностей и механизмов
процесса соударения. Обнаружено изменение поведения функции распределения по
 . Это изменение выразилось в смене режима от экспоненциальной . Это изменение выразилось в смене режима от экспоненциальной
(exp(-b )) зависимости к степенной ( )) зависимости к степенной (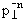 ) при существенном увеличении поперечного импульса ) при существенном увеличении поперечного импульса
 > 1 ГэВ/с и привело к разделению всех взаимодействий на „мягкие" и
„жесткие". > 1 ГэВ/с и привело к разделению всех взаимодействий на „мягкие" и
„жесткие".
Рис. 70: Иллюстрация универсальности процесса множественного рождения частиц,
проявляющейся в генерации кварковых и глюонных струй.
7.2.1 Основные особенности множественного рождения частиц
Изменение поведения функции распределения по
 можно объяснить включением
нового механизма при столкновении нуклонов: соударения между кварками, входящими
в состав нуклонов. Результатом таких столкновений на кварковом уровне является
рождение партонных струй (кварковых и глюонных), состоящих из адронов, узко
коллимированных вокруг направления движения партонов. Коллимация есть следствие
процесса адронизации партонов после развития партонного каскада. можно объяснить включением
нового механизма при столкновении нуклонов: соударения между кварками, входящими
в состав нуклонов. Результатом таких столкновений на кварковом уровне является
рождение партонных струй (кварковых и глюонных), состоящих из адронов, узко
коллимированных вокруг направления движения партонов. Коллимация есть следствие
процесса адронизации партонов после развития партонного каскада.
Рождение партонных струй происходит, когда поперечные импульсы частиц
превышают среднее значение.
Многочисленные эксперименты по изучению импульсных спектров частиц,
образующихся при множественных процессах, показали, что основная масса частиц
рождается с поперечными импульсами
 < 1
ГэВ/с, что приводит к < < 1
ГэВ/с, что приводит к < > ~ 0.3
ГэВ/с. Эти процессы называются мягкими. Однако с ростом энергии соударяющихся
адронов и продвижением в область > ~ 0.3
ГэВ/с. Эти процессы называются мягкими. Однако с ростом энергии соударяющихся
адронов и продвижением в область
 > 1 ГэВ/с был обнаружен новый механизм
множественного рождения частиц: через образование струй адронов в результате адронизации кварков и глюонов. Процесс адронизации находится в стадии
изучения. > 1 ГэВ/с был обнаружен новый механизм
множественного рождения частиц: через образование струй адронов в результате адронизации кварков и глюонов. Процесс адронизации находится в стадии
изучения.
Далее остановимся на результатах, полученных при изучении мягких
процессов.
Сопоставление характеристик множественного рождения при столкновениях частиц
различной природы может служить способом выделения различных механизмов этого
сложного процесса.
Вторичные частицы, возникающие в процессах множественного рождения, являются
в подавляющей своей массе адронами, однако редко, с небольшими сечениями
происходит генерация частиц не адронной природы (прямое рождение μ±, е±, γ).
Большое число теоретических моделей, претендующих на описание процессов
множественного рождения, предсказывает поведение средних множественностей,
распределений по множественностям и корреляций между отдельными частицами в
зависимости от энергии. В результате развития инклюзивного метода анализа
множественных процессов, появились гипотезы общего характера о свойствах инклюзивных
сечений в асимптотике. Все эти теоретические предсказания можно проверить в
экспериментах по изучению множественности.
При анализе проблемы множественности следует иметь в виду, что в большинстве
теорий рассматривается множественное рождение частиц nch, а в эксперименте
наблюдаются продукты распада резонансов; кроме того, многие предсказания
относятся к полному числу вторичных частиц, тогда как в эксперименте чаще всего
определяют число заряженных частиц.
При рассмотрении множественного рождения частиц различают полную
множественность n, множественность заряженных частиц nch, а также
множественность частиц различного сорта ni. Индекс i может принимать значения π-, π+, π0,
K±,0, p,
 и т.д. и т.д.
Множественность заряженных частиц на одно взаимодействие можно найти прямым
измерением числа частиц в каждом взаимодействии, а среднюю множественность
заряженных частиц − интегрированием одночастичных спектров в инклюзивных
реакциях.
Первый способ осуществляется при измерениях в пузырьковых камерах и в
фотоэмульсиях. В этом случае средняя множественность частиц типа с в инклюзивной
реакции а + b → с + X может быть представлена в виде
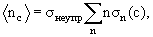
где σn(с) − эффективное сечение процесса генерации n раз частицы с
(топологическое сечение), σнеупр − эффективное сечение неупругого
взаимодействия.
При определении множественности интегрированием одночастичных спектров
средняя множественность вычисляется как интеграл от импульсного распределения
для простейшей нетривиальной инклюзивной реакции а + b → с + X, а именно
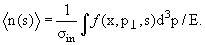
Изучение множественности вторичных частиц в адронных взаимодействиях −
весьма благодарная задача как для экспериментатора, так и для теоретика. В
экспериментах с помощью сравнительно простых технических и методических средств
можно получить обширную информацию, пригодную для непосредственного анализа и
сопоставления с теоретическими моделями. С теоретической точки зрения средняя
множественность и распределения по множественности (топологические сечения)
являются важнейшими пробными камнями различных моделей множественного рождения
частиц, причем, как правило, теоретические модели дают четкие предсказания
относительно распределения множественности и зависимости средней множественности
от энергии.
7.2.2 Топологическое сечение
Топологическое сечение описывает суммарное сечение всех каналов реакции,
приводящих к данному числу заряженных частиц n±:
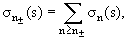
где n − полное число частиц в конечном состоянии. Сечение каждого канала σn(s) уменьшается с энергией, однако число возможных каналов растет с
увеличением s и поведение σn±(s) зависит от скорости убывания каждого канала и
от появления новых каналов реакции.
Топологические эффективные сечения лучше всего измерять с помощью пузырьковых
камер.
Экспериментальные данные о топологических сечениях в настоящее время
охватывают интервал от нескольких гигаэлектронвольт до 400 ГэВ в
рр-взаимодействиях, до 100 ГэВ в π+р- и рр-взаимодействиях, до 360 ГэВ в π-р-,
до 150 ГэВ в K-р- и до 33 ГэВ в K+р-взаимодействиях.
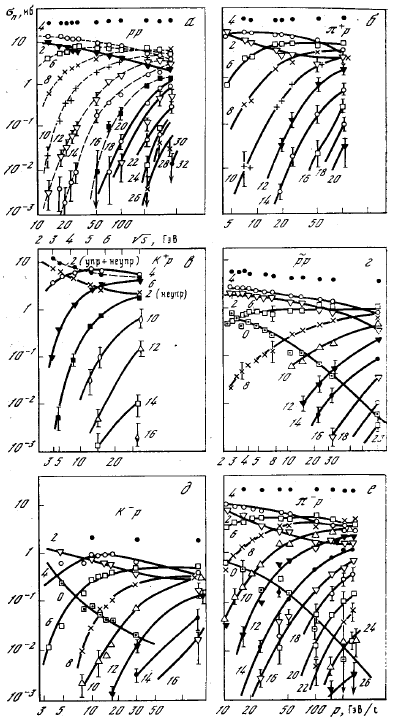
Рис. 71: Зависимость топологических неупругих эффективных сечений от импульса
налетающей частицы в лабораторной системе (кривые проведены от руки) для
различных взаимодействий. Цифры у кривых соответствуют значениям n±. |
На рис. 71а-е показаны энергетические зависимости топологических сечений для
рр-, π+р-, K+р-,
 р-, π-р- и K-р-взаимодействий. р-, π-р- и K-р-взаимодействий.
Основные общие особенности этих зависимостей следующие: 1) сечения σ0, σ2, σ4
уменьшаются с ростом энергии, остальные остаются постоянными или растут; 2) с
ростом энергии увеличивается вклад больших множественностей; 3) нуль-лучевые
топологические сечения (σ0) очень быстро падают с энергией по закону σ0 = ар-n, где а = 57 мб,
n = 1.51 ± 0.16 для π-р-реакции, а для рр-реакции а = 61
мб и
n = 1.46 ±0.15.
Из топологических эффективных сечений можно вычислить много параметров,
которые характеризуют распределения по множественности при заданной энергии.
Тщательное изучение свойств распределений с помощью анализа их моментов,
дисперсии D, отношений <n>/D и других параметров привело к формулировке
скейлинговых свойств по переменным: фейнмановской переменной x, быстроты и
скейлинговой множественности z = n/<n>.
Фейнмановский скейлинг для структурной функции (или импульсного спектра
вторичных частиц) формулируется в виде:
lim ƒ(x, ,s)s→∞ = ƒ(x, ,s)s→∞ = ƒ(x, ). Таким
образом, в пределе высоких энергий, когда импульсный спектр вторичных частиц
перестает зависеть от s, получаем для инклюзивной реакции а + b → с + X, что
средняя множественность с-частиц определяется соотношением ). Таким
образом, в пределе высоких энергий, когда импульсный спектр вторичных частиц
перестает зависеть от s, получаем для инклюзивной реакции а + b → с + X, что
средняя множественность с-частиц определяется соотношением
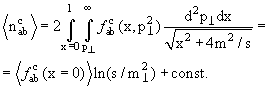
Очевидно, что фейнмановский скейлинг дает логарифмическую зависимость средней
множественности от s и постоянный предел (ƒ(x)) при малых х, если  ограничено. Коба, Нильсен и Олессен (KNO) показали, что фейнмановский скейлинг приводит к
скейлинговым распределениям по множественности. Число частиц n в конечном
состоянии должно быть функцией только переменной z = n/<n>, где <n> − средняя
множественность при данном √s. Этот результат может быть представлен в виде ограничено. Коба, Нильсен и Олессен (KNO) показали, что фейнмановский скейлинг приводит к
скейлинговым распределениям по множественности. Число частиц n в конечном
состоянии должно быть функцией только переменной z = n/<n>, где <n> − средняя
множественность при данном √s. Этот результат может быть представлен в виде
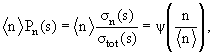
где σn(s) - топологическое эффективное сечение.
Скейлинговая форма по множественности, которая получила название
KNO-распределение, является универсальной для частиц любой природы и энергии,
если выполняется предположение о фейнмановском скейлинге.
На рис. 72 показано KNO-распределение для различных типов
соударяющихся частиц при различных энергиях.
Экспериментальные точки хорошо аппроксимируются универсальной кривой и
согласуются с предсказаниями KNO-скейлинга. Такой вывод можно сделать из анализа
данных для рр-взаимодействий в интервале энергий от 4 до 300 ГэВ. Сплошная
кривая на рисунке − результат аппроксимации экспериментальных данных единым
законом.
При энергиях, достигаемых на пересекающихся накопительных кольцах (ПНК) для
рр-соударений, эта аппроксимация так же описывает эксперимент. Однако более
детальный анализ с использованием моментов распределения показывает отклонение
от универсальной зависимости (рис. 73).
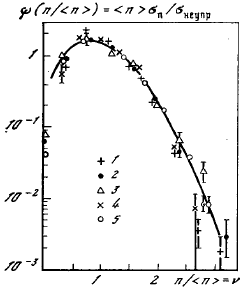
Рис. 72: Распределение К NO для разных типов соударяющихся частиц. Линия − аппроксимация данных
pp-взаимодействий в виде ψ(n/<n>) = <n>σn(s)/σtot(s).
1-3 − К+р, К-р,
 p-соударения при 32 ГэВ/с; 4, 5 − π+р-, π-р-соударения при 50 ГэВ/с. p-соударения при 32 ГэВ/с; 4, 5 − π+р-, π-р-соударения при 50 ГэВ/с. |
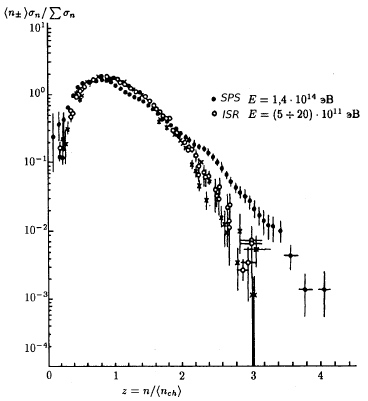
Рис. 73: KNO-распределение для разных энергий первичных частиц. |
Отклонение от универсальной зависимости при низких энергиях наблюдается для
положительно заряженных первичных частиц (π+, К+). Существуют различные
теоретические аппроксимации KNO-зависимости.
Средняя множественность <n> в зависимости от энергии для
pp-столкновения
показана на рис. 74. Результаты при высоких энергиях получены с помощью
стриммерной камеры в pp-столкновениях на ПНК (ISR).
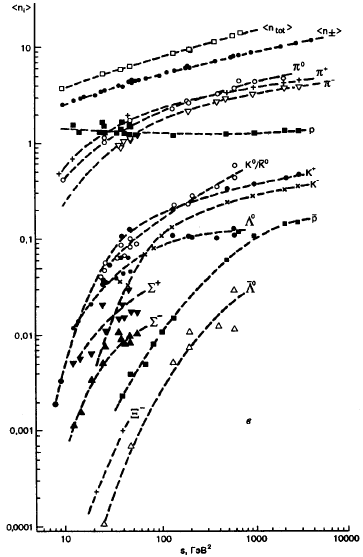
Рис. 74: Зависимость средней множественности заряженных частиц разной природы
в рр-соударениях от квадрата полной энергии s.
7.2.3 Теоретические предсказания
Существующие теоретические модели предсказывают разную зависимость от s
средней множественности. Их можно разделить на группы по типу ожидаемых закономерностей.
1. Одна группа моделей объединяет статистические,
термодинамические и гидродинамические теории. Все они предсказывают степенную
зависимость средней множественности от энергии. Процесс взаимодействия
рассматривается через образование компаунд-системы, достигающей той или иной
степени равновесия. При распаде системы частицы разлетаются, при этом можно
учитывать взаимодействие частиц (модель Ландау) или не учитывать его (модель
Ферми). Обе эти модели дают одинаковые предсказания относительно зависимости
средней множественности от энергии:
<n> ~ (s/m2)l/4,
где s − квадрат полной энергии в СЦМ, m − масса нуклона. Если учесть вязкость
в процессе расширения статистической системы, то зависимость множественности от
энергии получается в виде
<n> ~ (s/m2)1/3.
2. Другая группа моделей представлена периферическими моделями. Эта
группа моделей дает логарифмический рост множественности с энергией
<n> = а + b ln(s/m2).
или
<n> = c ln(s/m2).
3. Третья группа моделей − асимптотические, предсказывающие поведение
инвариантных дифференциальных сечений
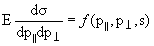
при s → ∞. Они выдвинуты в работах Р. Фейнмана, С. Янга. Согласно гипотезе
Фейнмана
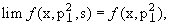
где х =
 /E =
2 /E =
2 */√s − переменная Фейнмана, а */√s − переменная Фейнмана, а
 и и
 − составляющие импульса,
т.е. при больших энергиях инклюзивные сечения не зависят явно от энергии, а
определяются масштабными переменными х и − составляющие импульса,
т.е. при больших энергиях инклюзивные сечения не зависят явно от энергии, а
определяются масштабными переменными х и
 2 (гипотеза скейлинга). 2 (гипотеза скейлинга).
Если
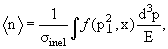
то при учете асимптотического поведения ƒ(p,s) можно получить следующее
соотношение:
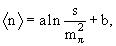
т.е. в асимптотике должен наблюдаться логарифмический рост
множественности.
4. Модель полюсов Редже дает следующее предсказание о поведении
множественности с энергией
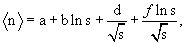
т.е. более сложный логарифмический рост.
Сравнение с экспериментальными данными показывает, что наилучшее описание
соответствует логарифмической зависимости средней множественности от s (пункты 3 и 4).
Рассмотрим далее распределение по множественности заряженных частиц
n±, т.е.
разные виды функции Pn(s) = σn(s)/σtot. Можно, например, представить функцию Pn(s) в
виде распределения Пуассона. Распределение Пуассона или нормальное распределение
может быть записано в терминах KNO-скейлинговых переменных z и (D/<n>)2, которые должны быть константами. Но Пуассон не описывает распределение
заряженных частиц по множественности. Функция, близко соответствующая Пуассону,
есть Gamma-распределение, которое может быть записано в виде
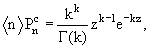
z = n/<n>, k-l = (D/<n>)2
и хорошо описывает полную множественность, но не подходит для описания
распределения по множественности заряженных частиц.
Функция, которая успешно используется для описания распределения по
множественности заряженных частиц, есть негативное биномиальное (NB)
распределение
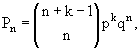
где Pn − вероятность наблюдения величины п, в то время как ожидается величина
k.
Негативное биномиальное (NB) распределение в терминах k и <n> имеет вид
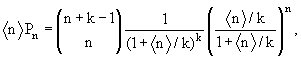
(D/n)2 = 1/k + 1/<n>.
При этом если <п> >> k > 1, NB → Gamma; если k → ∞, NB → Poisson.
NB-распределение хорошо описывает множественности заряженных частиц в
ограниченной области псевдорапидити (псевдобыстроты). При достаточно высоких <n>
]NB-распределение есть KNO-скейлинговая функция, если к не зависит от
энергии. При фитировании распределений с различными энергиями вплоть до √s =
900 ГэВ было найдено, что параметр k уменьшается с энергией и KNO-скейлинг
нарушается.
7.3 Импульсные спектры вторичных частиц
Импульсные спектры вторичных частиц несут интересную информацию о динамике
процесса множественного рождения. Очень часто продольную и поперечную компоненты
импульсов вторичных частиц рассматривают раздельно, и вводится предположение о
независимости распределений по продольному и поперечному импульсам - так
называемая „факторизация". Тогда инклюзивное инвариантное сечение можно записать
в виде
E(d3σ/dp3) = F1(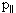 ,s)F2( ,s)F2( ) = ƒ(s,p). ) = ƒ(s,p).
Соотношение между двумя составляющими импульса − продольной и поперечной
хорошо видно на диаграмме Пейроу (рис. 75). Здесь по оси абсцисс отложена
продольная компонента импульса в СЦМ, а по оси ординат - поперечная компонента.
Каждая частица изображается на диаграмме точкой. Разрешенная область (или
фазовый объем), определяемая законами сохранения, заключена внутри
полуокружностей. Из диаграммы видно, что для протонов и пионов продольные
импульсы достигают кинематической границы, а поперечные импульсы − не достигают.
Это важное различие в поведении продольной и поперечной компонент импульса
вторичных частиц. Кроме того, продольная компонента зависит от многих
кинематических особенностей, в то время как поперечная компонента является
лоренц-инвариантом.
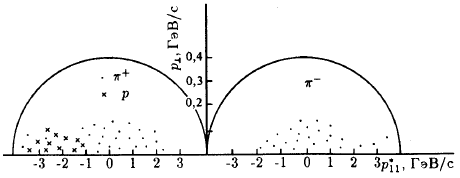
Рис. 75: Диаграмма Пейроу для π-р-столкновения: точки − π-- и π+-мезоны; крестики − протоны.
7.3.1 Поперечный импульс
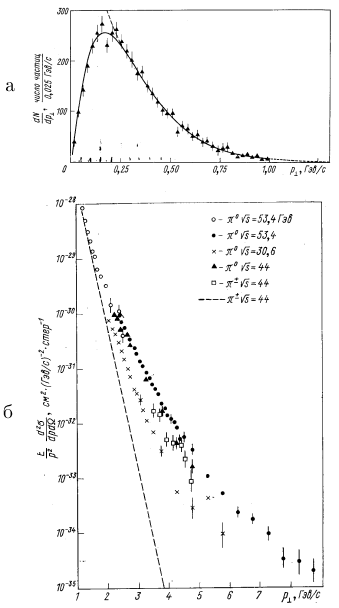 Рис. 76: Распределение поперечных импульсов:
а − для области малых и средних
поперечных импульсов; б − для области больших поперечных импульсов; штриховая
линия - экстраполяция распределения из области
 < 1 ГэВ/с. < 1 ГэВ/с. |
Основные свойства поперечного импульса: 1) ограниченность
 и его малая
величина; 2) слабая зависимость от энергии и природы первичной частицы. Эти
свойства были впервые обнаружены в космических лучах, подтверждены данными
ускорительных экспериментов и в настоящее время используются при построении
многих теоретических моделей. и его малая
величина; 2) слабая зависимость от энергии и природы первичной частицы. Эти
свойства были впервые обнаружены в космических лучах, подтверждены данными
ускорительных экспериментов и в настоящее время используются при построении
многих теоретических моделей.
Распределение поперечных импульсов слабо зависит от энергии и множественности
вторичных частиц. Оно показано на рис. 76.
Из рисунка видно, что интервал значений
 можно условно разбить на 3
области: область малых поперечных импульсов можно условно разбить на 3
области: область малых поперечных импульсов
 < 0.1 ГэВ/с, область средних
поперечных импульсов < 0.1 ГэВ/с, область средних
поперечных импульсов
0.1 <
 < 1 ГэВ/с и область больших поперечных
импульсов < 1 ГэВ/с и область больших поперечных
импульсов
 > 1 ГэВ/с. > 1 ГэВ/с.
В процессах множественного рождения, идущих с большим сечением, основная доля
вторичных частиц имеет поперечные импульсы, заключенные в области
 < 1 ГэВ/с. Здесь распределение по < 1 ГэВ/с. Здесь распределение по
 можно описать экспоненциальной функцией можно описать экспоненциальной функцией
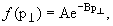
где В ~ 6. Величина среднего поперечного импульса, полученная
экспериментально для пионов, составляет 350 МэВ/с, для каонов
~ 450 МэВ/с, для
нуклонов ~ 500 МэВ/с. Средний поперечный импульс можно вычислить из
соотношения:
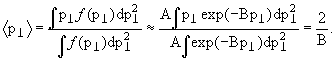
Третья область содержит поперечные импульсы больше 1 ГэВ/с. В частности,
эксперименты, проведенные на установке ПНК в ЦЕРН при энергии до 2000 ГэВ,
показали, что с ростом энергии могут появляться вторичные частицы с большими
 ~ (3 ÷8) ГэВ/с. Вероятность появления таких частиц мала (~ 10-4). Кроме того,
при значениях
~ (3 ÷8) ГэВ/с. Вероятность появления таких частиц мала (~ 10-4). Кроме того,
при значениях
 > 2 ГэВ/с распределение по поперечным импульсам ƒ( > 2 ГэВ/с распределение по поперечным импульсам ƒ( ) вместо
экспоненциального становится степенным. Изменение формы распределения, переход
на более пологую, степенную зависимость (рис. 766) можно связать с проявлением
внутренней структуры нуклонов. Можно предположить, что частицы с большими
поперечными импульсами появляются в результате жестких (глубоко неупругих)
соударений кварков из сталкивающихся нуклонов. После жесткого соударения
провзаимодействовавшие кварки адронизуются и образуют струи адронов − потоки
частиц, коллимированные в малом телесном угле (рис. 77а). ) вместо
экспоненциального становится степенным. Изменение формы распределения, переход
на более пологую, степенную зависимость (рис. 766) можно связать с проявлением
внутренней структуры нуклонов. Можно предположить, что частицы с большими
поперечными импульсами появляются в результате жестких (глубоко неупругих)
соударений кварков из сталкивающихся нуклонов. После жесткого соударения
провзаимодействовавшие кварки адронизуются и образуют струи адронов − потоки
частиц, коллимированные в малом телесном угле (рис. 77а).
Образование струй в процессах сильного взаимодействия адронов интенсивно
изучалось в экспериментах на ПНК- и SPS-коллайдерах в ЦЕРН.
Распределения по
 измерены до значений ~ 36 ГэВ/с. измерены до значений ~ 36 ГэВ/с.
Большинство теоретических моделей представляет инвариантное эффективное
сечение для генерации частиц с
 > 2 ГэВ/с в форме > 2 ГэВ/с в форме
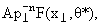
где 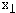 = 2 = 2 /√s, θ* - угол в СЦМ столкновения. /√s, θ* - угол в СЦМ столкновения.
В измерениях на ПНК при √s от 23 до 62 ГэВ и х < 0.3 было получено для
π0-мезонов, генерирующихся под углом 90°, выражение вида
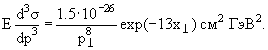
На рис. 776 показаны инвариантные эффективные сечения для инклюзивной генерации π0-мезонов в зависимости от
 , для √s = 53, 200,
800 ГэВ. Аналогичные зависимости имеют место и для , для √s = 53, 200,
800 ГэВ. Аналогичные зависимости имеют место и для
π±-мезонов, изменяются только значения нормирующих
коэффициентов.
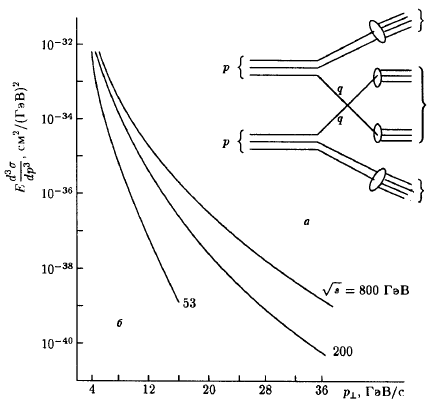
Рис. 77: Образование струй в процессах сильного взаимодействия: а − диаграмма
жесткого соударения; б − инвариантное эффективное сечение для генерации π0-мезонов при разных энергиях.
Полученные результаты хорошо интерпретируются в рамках КХД модели,
рассматривающей процесс жесткого рассеяния кварков из сталкивающихся адронов по
схеме рис. 77а.
Детальное исследование характеристик струй (множественности и природы частиц
в них) выполнялись на ускорителях с встречными
электрон-позитронными пучками, а также на SPS-коллайдере, на Тэватроне 1 (ФНАЛ)
и на ускорителе LEP в ЦЕРН.
Зависимость поперечного импульса от природы первичной частицы слаба или
отсутствует, т.е. для первичных частиц любой природы форма распределения по
 не меняется. не меняется.
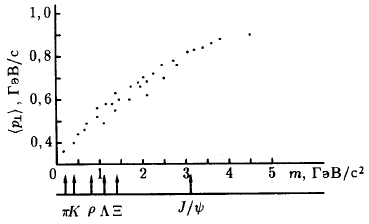 Рис. 78: Зависимость ( ) от массы родившейся частицы или системы из
n частиц, имеющей эффективную массу, равную m. ) от массы родившейся частицы или системы из
n частиц, имеющей эффективную массу, равную m. |
На рис. 78 показана найденная на опыте зависимость среднего значения поперечного импульса ( ) от природы вторичной частицы. Из
рисунка видно, что наблюдается некоторый рост ( ) от природы вторичной частицы. Из
рисунка видно, что наблюдается некоторый рост ( ) с ростом массы частицы.
Наиболее наглядное объяснение этого эффекта существует в моделях
гидродинамического типа. После образования возбужденной компаунд-системы
начинается процесс ее остывания. Когда система остывает до температуры,
соответствующей массе покоя какой-нибудь реальной частицы, она вылетает из
системы. В конечном состоянии система охлаждается до температуры кТ ~ 140 МэВ и
распадается на пионы. Чем меньше температура системы, тем меньший поперечный
импульс уносит частица. Этот же эффект лежит в основе объяснения наблюдаемого на
опыте слабого роста ( ) с ростом массы частицы.
Наиболее наглядное объяснение этого эффекта существует в моделях
гидродинамического типа. После образования возбужденной компаунд-системы
начинается процесс ее остывания. Когда система остывает до температуры,
соответствующей массе покоя какой-нибудь реальной частицы, она вылетает из
системы. В конечном состоянии система охлаждается до температуры кТ ~ 140 МэВ и
распадается на пионы. Чем меньше температура системы, тем меньший поперечный
импульс уносит частица. Этот же эффект лежит в основе объяснения наблюдаемого на
опыте слабого роста ( ) при увеличении энергии первичной частицы. На рис. 79
представлены результаты измерений ( ) при увеличении энергии первичной частицы. На рис. 79
представлены результаты измерений ( ), выполненных на ускорителях и в космических лучах. ), выполненных на ускорителях и в космических лучах.
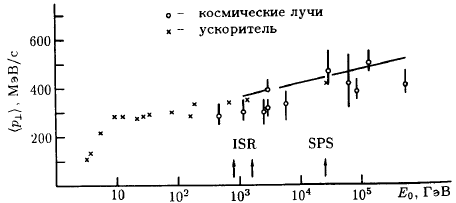
Рис. 79: Зависимость (р±) от энергии первичной частицы: сплошная линия − расчет по гидродинамической модели.
7.3.2 Продольный импульс
Спектры продольных импульсов, измеренные в лабораторной системе координат и
представленные в форме двойных дифференциальных сечений
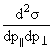 , можно использовать
для изучения процессов фрагментации налетающей частицы. Те же спектры,
рассмотренные в зеркальной (антилабораторной) системе координат, дают сведения о
процессах фрагментации частицы мишени. , можно использовать
для изучения процессов фрагментации налетающей частицы. Те же спектры,
рассмотренные в зеркальной (антилабораторной) системе координат, дают сведения о
процессах фрагментации частицы мишени.
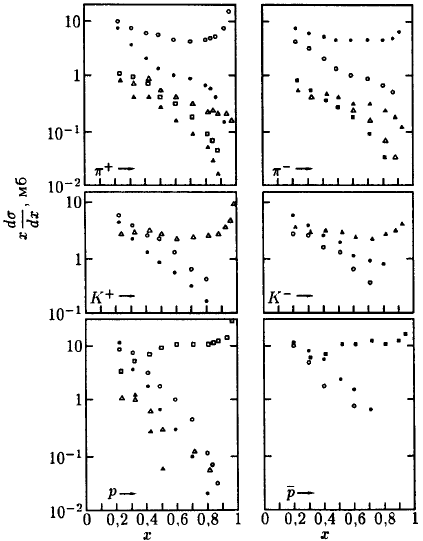
Наиболее часто импульсные спектры анализируются в СЦМ соударения по
переменной Фейнмана
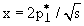 . На рис. 80 показаны спектры в инвариантной
форме . На рис. 80 показаны спектры в инвариантной
форме
х(dσ/dx) для соударения частиц различной природы с протонами при энергии
первичных частиц 100 ГэВ.
Главная особенность импульсных спектров для всех реакций - это четкое
проявление эффекта лидирования. Спектры вторичных частиц, природа которых
совпадает с природой налетающей частицы, имеют подобный вид и свидетельствуют о
равномерном распределении энергии таких частиц по всему интервалу x от 0 до 1.
Будем называть их лидирующими частицами, поскольку они уносят основную энергию
после столкновения. Спектры лидирующих частиц характеризуют распределения
коэффициентов неупругости, так как жлид = 1 − K, где K - коэффициент неупругости
соударения. Таким образом, изучая спектры лидирующих частиц по переменной х (или
при высокой энергии по переменной
u = Елид/Е0 в L-системе), получаем информацию
о важнейшем параметре взаимодействия − полном коэффициенте неупругости.
Спектры частиц иной, чем первичная частица, природы имеют на графике вид
круто спадающих зависимостей.
Однако эффект лидирования сказывается на быстроте падения дифференциальных
сечений с х. Если вторичная частица имеет тот же электрический заряд, что и
налетающая, то спектры более пологие, чем в том случае, когда знак заряда
вторичной частицы противоположен знаку заряда налетающей частицы.
Из вида этих спектров можно получить долю частиц разной природы, рождающихся
в различных соударениях.
Изучение спектров вторичных частиц при различных энергиях первичных позволяет
ответить на вопрос о том, существует ли скейлинговое поведение спектров в
области фрагментации налетающей частицы. Для этого необходимы эксперименты при
существенно различных энергиях первичных частиц, так как отклонение от
скейлингового поведения спектров незначительно и заключено в пределах ~ 10%.
7.3.3 Коэффициент неупругости
Коэффициент неупругости определяет долю энергии, затраченной первичной
частицей на образование новых частиц. Полный коэффициент неупругости K = ∑Еi/Е0, где Еi − энергия вторичной частицы
i-той природы, Е0 − энергия
первичной частицы. Для определения полного коэффициента неупругости суммируются
энергии всех вторичных частиц, кроме энергии лидирующей частицы. Если же
суммируются энергии частиц какой-либо одной природы (например, энергии π0-мезонов или
K±-мезонов и т.д.), то определяется парциальный коэффициент
неупругости. Можно определить полный коэффициент неупругости, измерив энергию,
унесенную лидирующей (сохранившейся) частицей − Елид, тогда
K = 1 − Елид/Е0 = 1 − uлид.
Отсюда видно, что распределение полных коэффициентов неупругости
представляется импульсным спектром лидирующих частиц. Как уже упоминалось, при
высоких энергиях переменная х и мЛИд совпадают. Таким образом, спектры
лидирующих частиц, изображенные на рис. 80 для различных реакций, дают
распределения полных коэффициентов неупругости в этих реакциях. Значения
xлид =
1 соответствуют значениям K = 0, т.е. упругим соударениям. Эта особенность
подчеркивается ростом сечения в области xлид → 1 для лидирующих частиц любой
природы. Данные об области х < 0.2, т.е. К > 0.8 в распределениях на рис.
80 отсутствуют. Следует отметить, что в распределениях для лидирующих протонов
сечение начинает уменьшаться уже при значениях xpлид = 0.5. Сечение со
значениями xpлид = 0.2 (K = 0.8) в два раза меньше, чем сечение с хpлид = 0.5.
Этот эффект отсутствует в спектрах лидирующих частиц другой природы, не
совпадающей с природой первичной частицы.
Указанное явление связано с сохранением барионного числа и приводит к тому,
что среднее значение коэффициента неупругости для нуклонов составляет K = 0.5. Эффект сохранения в космических лучах проявляется при прохождении первичного
космического излучения через атмосферу Земли, в ядерно-каскадном процессе, при
образовании широких атмосферных ливней.
Именно в этой связи изучению полного и парциальных коэффициентов неупругости
в космических экспериментах уделялось большое внимание. На рис. 81а,б,в
показаны распределения парциальных коэффициентов неупругости а при взаимодействии
космических протонов, нейтронов и пионов с ядрами. Результаты получены на
установке "Пион" на высокогорной станции Арагац (3260 м над уровнем моря) при
энергии первичных частиц от 500 до 1000 ГэВ.
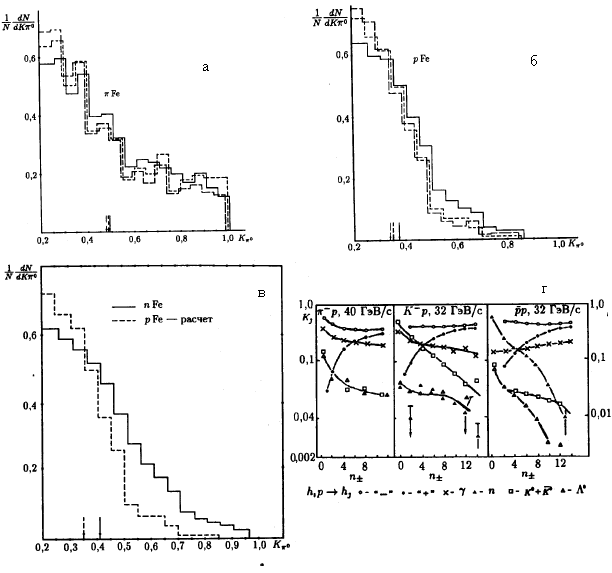
Рис. 81: Распределение парциальных коэффициентов неупругости при
взаимодействии: а − пионов, б − протонов и в − нейтронов с ядрами железа; г − средние значения парциальных коэффициентов неупругости в зависимости от
множественности заряженных частиц в π-р-, К-р-,
 р-взаимодействиях для
вторичных частиц различной природы. р-взаимодействиях для
вторичных частиц различной природы.
Точные данные о значениях коэффициентов неупругости, зависимости его от
энергии, от множественности и от природы сталкивающихся частиц получены в
экспериментах на ускорителях (рис. 81г). Из этих же данных можно видеть, как
зависят парциальные коэффициенты неупругости от природы налетающей частицы и от
природы вторичных рождающихся адронов.
Для выяснения зависимости коэффициентов неупругости от энергии налетающей
частицы необходимы данные экспериментов при более высоких энергиях, которые в
настоящее время отсутствуют.
Из экспериментов, выполненных в космических лучах косвенными методами, можно
сделать заключение, что коэффициенты неупругости, если и зависят от энергии, то
очень слабо.
Изучение коэффициентов неупругости при взаимодействии нуклонов с атомными
ядрами при ускорительных энергиях (до 200÷300 ГэВ) показало практическое
отсутствие какой-либо зависимости K от А − атомного номера ядра мишени при
точности эксперимента, заключенной в пределах 10÷15%. Необходимы более
детальные исследования.
7.3.4 Основные переменные, использующиеся при анализе угловых распределений
вторичных частиц
Для исследования углового распределения могут быть использованы различные
переменные. Например, можно изучать распределение dN/dΩ, где dΩ = 2π sin θ dθ − элемент телесного угла. Это распределение можно записать в виде
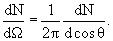
Однако из-за сильного влияния кинематических эффектов в L-системе это
распределение заключено в интервале самых малых значений аргумента и сильно
зависит от величины s. Поэтому его трудно использовать для анализа
экспериментальных результатов в L-системе. Чаще всего оно используется в
С-системе. Удобнее другая форма представления углового распределения в
переменной λ = lg tan θ или η = − ln tan (θ/2).
Величину η называют псевдобыстротой, так как она при высоких энергиях
сталкивающихся частиц, когда р = Е, совпадает с быстротой у:
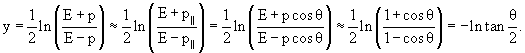
Для анализа угловых распределений в эвентуальном подходе часто используются
параметры γs и γc − лоренц-факторы симметричной S-системы и С-системы
соответственно. Величины ξ = lg(γs/γc) или γsc
= (1/2)(γs/γc + γc/γs) характеризуют степень
асимметрии индивидуального события, поэтому их называют параметрами асимметрии.
В области высоких энергий, когда Ei = pi = mi
(с = 1), γs определяется
соотношением
lg γs = −<lg tg θi>,
где θi − угол вылета частицы в L-системе, а
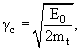
где E0 − энергия налетающей частицы, а mt − масса частицы-мишени.
Другим параметром асимметрии углового распределения может служить величина α, определяемая как отношение
α = (nf − nb)/(nf + nb),
где nf и nb − числа заряженных частиц, вылетающих вперед и назад в С-системе
соответственно.
7.3.5 Угловые распределения в С-системе
Угловое распределение вторичных частиц в адрон-адронных соударениях при
высоких энергиях резко анизотропно в С-системе (рис. 82), т.е. вторичные
частицы, как правило, разлетаются в противоположных направлениях в виде двух
струй адронов в системе центра масс соударения.
Однако эвентуальный анализ событий показывает, что в индивидуальных событиях
разлет частиц может быть существенно асимметричен в С-системе.
На рис. 83 показано распределение событий по параметру асимметрии γsc для π-р-соударений при 40 ГэВ/с. Оно имеет резко выраженный асимметричный
характер.
|
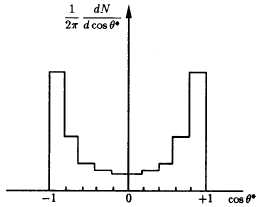
Рис. 82: Угловое распределение вторичных частиц в С-системе для
рр-соударений. |
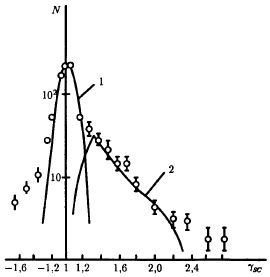
Рис. 83: Распределение событий по параметру γsc для π-р-взаимодействий при
40 ГэВ/с:
1 − распределение погрешностей (гауссовская кривая с дисперсией D2 =
0.082); 2 − распределение γsc в модели для ππ-соударения. |
В случае рр-соударений аналогичное распределение описывается симметричной
кривой гауссовского типа с дисперсией D2 = 0.142, которая несколько шире, чем
кривая 1 на рис. 83.
Такой вид угловых распределений хорошо согласуется с импульсными спектрами
вторичных частиц, рассмотренных ранее, и свидетельствует о различии динамики
взаимодействий пионов и протонов с нуклонами, обусловленном различием их
кварковой структуры.
7.4 Распределения по η
и y
Распределения вторичных частиц по псевдобыстроте интенсивно исследуются в
экспериментах на крупнейших современных ускорителях в ЦЕРН и в Фермиевской
национальной лаборатории. Результаты этих исследований показаны на рис. 84 для
положительных значений η
или у. В области η
< 0 распределения полностью
симметричны приведенным.
Гипотеза скейлинга требует, чтобы эффективные сечения (1/σ)(dσ/dη) при η
= 0 не
изменялись с ростом энергии первичных частиц. Однако, как видно из рис. 84, это
требование не выполняется, и скейлинг в центральной области не наблюдается при
существующих энергиях. На рис. 85 показана зависимость (1/σ)(dσ/dη)|η=0 от энергии.
Очевидно, что это логарифмическая зависимость.
Исследование распределений по псевдобыстроте, а точнее по величине λ, интенсивно проводилось в середине 60-х годов в экспериментах с космическими
лучами. Были получены результаты, аналогичные приведенным на рис. 84 (кривые 2 и
3). Провал в центральной области при λ = 0 был интерпретирован в ряде работ как результат образования в С-системе
сгустков возбужденной материи − файрболов, разлетающихся в противоположных
направлениях в С-системе и распадающихся изотропно в собственной системе покоя.
Однако, как показал тщательный анализ и сравнение переменных η
и у, провал в
центре распределения обусловлен кинематическими, а не динамическими
эффектами.
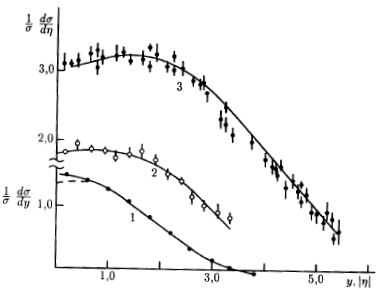
Рис. 84: Распределение вторичных заряженных частиц по псевдобыстроте и
быстроте при разных энергиях соударяющихся нуклонов: 1 − для рр-соударений при
E0 = 205 ГэВ; 2 − рр-соударения при √s = 53 ГэВ, Е0 = 1400 ГэВ; 3 -
рр-соударения, √s = 540 ГэВ, Е0 = 1.4·104 ГэВ.
Различие между псевдобыстротой η
и быстротой у состоит в том, что при
вычислении быстроты требуется знание энергии и импульса, т.е. природы вторичной
частицы.
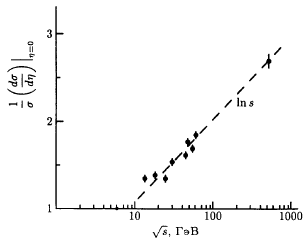
Рис. 85: Зависимость сечения в центральной области от энергии в
С-системе.
Для вычисления псевдобыстроты необходим только угол вылета частицы θ. Следствием этого становится появление провала в распределении по η
(или λ) и отсутствие такового в распределении по у (рис. 84, кривая 1, пунктиром показано
распределение по η
для этих же данных).
7.5 Дифракционная генерация
Особое место среди процессов множественного рождения частиц занимает явление
дифракционной генерации. По многим характеристикам этот процесс сходен с
процессом упругого рассеяния, что дает возможность провести аналогию с процессом
классической дифракции световых волн и использовать оптические модели для
описания общих свойств дифракционной генерации.
Однако явление неупругой дифракционной генерации принципиально отличается от
упругого рассеяния, так как приводит к образованию новых вторичных частиц.
Явление дифракционной генерации (рис. 86) состоит в том, что в поле нуклона-мишени налетающая частица возбуждается, а затем
возбужденная система распадается и образует несколько быстрых частиц с
импульсами, лежащими в области фрагментации возбуждающейся частицы. При этом
квантовые числа возбужденной системы и нуклона-мишени не меняются. На языке
Фейнмана этот процесс можно изобразить как обмен помероном.
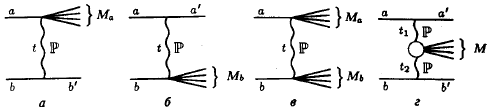
Рис. 86: Схема дифракционного процесса: а − с возбуждением налетающей частицы
(σ'D); б − с возбуждением нуклона-мишени (σ"D)); в − двойной дифракции
(σDD), г − двухпомеронного обмена (σ'DIP).
Так как померон имеет нулевые квантовые числа, то обмен этой траекторией не
приводит к изменению квантовых чисел в каждой из вершин. Нуклон-мишень получает
небольшой импульс отдачи (рис. 86а).
Этот процесс может протекать и с возбуждением частицы-мишени (рис. 866) или с
возбуждением и налетающей частицы, и частицы-мишени (рис. 86в), а также
посредством обмена двумя померонами − двухпомеронный обмен (рис. 86г) или виртуальное померон-померонное взаимодействие.
Группа образующихся частиц с массой Мa2 или
Мb2 имеет такие же квантовые числа
(заряд, изосиии, барионное число, странность) как частица а или b. Спин и
четность могут отличаться в соответствии с изменением орбитального момента
группы частиц Ма или Мb-
7.5.2 Основные особенности процесса дифракционной генерации
Процессы дифракционной генерации удобно описывать в переменных
МX2, s и t, где
МX2 = ( a − a −
 b)2 − квадрат эффективной массы системы частиц
X, где X = а или b, t
= ( b)2 − квадрат эффективной массы системы частиц
X, где X = а или b, t
= ( b − b −
 b')2 − квадрат четырех-импульса, переданного адрону, оставшемуся
невозбужденным, s = ( b')2 − квадрат четырех-импульса, переданного адрону, оставшемуся
невозбужденным, s = ( a + a +
 b)2 − квадрат полной энергии столкновения в СЦМ. b)2 − квадрат полной энергии столкновения в СЦМ.
В приближении больших энергий √s и малых эффективных масс Мх связь между
этими переменными дается соотношениями
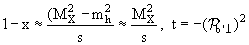
при s → ∞, МX2 ≈ mh2. Здесь х − переменная Фейнмана, х = 2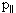 */√s, mh − масса адрона а или b, */√s, mh − масса адрона а или b,
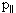 и и
 − продольная и поперечная компоненты
импульса. − продольная и поперечная компоненты
импульса.
Отсюда масса образовавшейся дифракционной системы будет следующей:
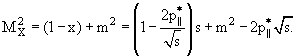
7.5.3 Характеристики дифракционного рождения
Средняя множественность в событиях с дифракционной генерацией
<n±>0 меньше,
чем полная средняя множественность при данной энергии. В интервале энергий
100÷400 ГэВ в рр-столкновениях
<n±>D ~ (1/2)<n±>.
Низкая множественность в процессах дифракционной генерации объясняется
преимущественным рождением малых масс.
Эксперименты показывают, что средняя множественность дифракционных частиц в
интервале М2 от 10 до 400 (ГэВ)2 может быть описана логарифмической
зависимостью
<n±>D = а + b ln М2
для π-р- и рр-взаимодействий. При этом коэффициент b одинаков для π-р- и
рр-взаимодействий, т.е. множественность дифракционных частиц не зависит от сорта
сталкивающихся частиц и от начальной энергии.
Полное сечение дифракционной генерации складывается из сечений различных
каналов:
σDtot = σ'D + σ"D + σDD + σDIP,
где σ'D и σ"D определяют сечение дифракционной генерации в одной из вершин
(рис. 86), σDD − сечение двойной дифракционной генерации, σDIP − сечение
двухпомеронной дифракции, σDIP − сечение мало, примерно на три порядка меньше
полного.
Эксперименты показывают слабую зависимость сечения дифракционной генерации σ'D от первичной энергии; при энергиях 300÷400 ГэВ эта зависимость может быть
представлена в виде
σ'D ~ s-0.35.
Дифференциальное сечение
dσ/dt также является важной характеристикой
дифракционного процесса. Поведение dσ/dt для малых углов рассеяния можно описать
экспоненциальной зависимостью
dσ/dt = Aexp[−BD(M2)t],
где BD − наклон дифракционного конуса, который определяется только величиной
МX2 и не зависит от начальной энергии взаимодействия.
При увеличении размеров мишени, например при дифракционном процессе на ядре,
состоящем из А нуклонов, должны уменьшаться углы разлета вторичных частиц. Таким
образом, углы разлета могут служить отличием дифракционных процессов рождения
частиц, идущих на ядре в целом, от процессов на отдельных нуклонах ядра.
7.6 Теоретические модели. Механизмы множественной генерации частиц
При описании множественных процессов возникают как математические трудности,
связанные с наличием многих частиц, так и трудности из-за отсутствия единой
теории сильных взаимодействий. Существует много моделей, описывающих те или иные
особенности множественных процессов. Исторически раньше других появились модели статистического и
гидродинамического типа, затем возникли мультипериферические модели.
7.6.1 Статистическая и гидродинамическая модели
Тот факт, что в результате множественного рождения возникает большое число
частиц, наводит на мысль об установлении статистического равновесия в процессе
взаимодействия. Первоначальный вариант статистической модели для описания
множественных процессов был предложен Э.Ферми в 1959 году. В его работе
использовалась модель идеального газа. Сечение процесса
а + b → c1 +
c2 +
... + сn можно представить как произведение структурной функции на инвариантный
фазовый объем:
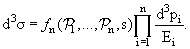
По гипотезе Ферми сечение процесса множественного рождения должно быть
пропорционально фазовому объему, т.е. ƒn( 1,..., 1,...,
 n,s) = const. Модель, при
которой весь фазовый объем равномерно заполнен состояниями системы, называется
статистической. Процесс множественного рождения в этом случае состоит в
следующем: сталкивающиеся адроны образуют общую систему, в которой выделяется
вся их энергия, определяющая температуру системы Т. Внутри объема системы
происходит сильное взаимодействие квантов ядерного поля, в результате чего в
объеме устанавливается равновесное состояние, которое можно рассматривать
статистически. Объем системы Ω представляет собой лоренцево сжатую сферу радиуса сильных взаимодействий n,s) = const. Модель, при
которой весь фазовый объем равномерно заполнен состояниями системы, называется
статистической. Процесс множественного рождения в этом случае состоит в
следующем: сталкивающиеся адроны образуют общую систему, в которой выделяется
вся их энергия, определяющая температуру системы Т. Внутри объема системы
происходит сильное взаимодействие квантов ядерного поля, в результате чего в
объеме устанавливается равновесное состояние, которое можно рассматривать
статистически. Объем системы Ω представляет собой лоренцево сжатую сферу радиуса сильных взаимодействий
r0 = ћ/mπс:
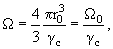
где γс = Е*/mс2, Е* - полная энергия в СЦМ. После взаимодействия начинается
разлет частиц, во время которого по предположению Ферми частицы не
взаимодействуют, что позволяет описать состояние системы с помощью уравнений
термодинамики идеального газа.
Используя закон Стефана-Больцмана, который для плотности энергии ε дает
зависимость
ε ~ (кТ)4, Ферми получил
Е* ~ Ω(кТ)4, Ω = Ω0/γс
= Ω0mc2/E*, Е* ~ Ω0mc2(kT)4/E*,
Е*2 ~ Ω0mc2(kT)4, Е* ~
(Ω0mc2)1/2(kT)2.
При равномерном распределении энергии по степеням свободы энергия каждой
частицы пропорциональна кТ, а полное число частиц связано с энергией Е*
соотношением
n = E*/(kT) ~ (E*)1/2 ~ E1/4,
где Е - энергия в лабораторной системе.
Таким образом, статистическая модель предсказывает зависимость
множественности от энергии в виде Е1/4. Другие варианты статистической модели
предсказывают иные зависимости: n ~ Е1/3 и
n ~ Е1/2, но во всех случаях они
являются степенными. В этих моделях частицы образуются фактически в момент
столкновения.
Точка зрения Ферми подверглась критике со стороны Л.Д. Ландау. Действительно,
в первый момент взаимодействия, когда образовалась общая система и между
частицами системы существует сильное взаимодействие, нельзя вообще говорить о
числе частиц, так как в результате сильного взаимодействия они непрерывно
рождаются и исчезают. Такой процесс будет происходить до тех пор, пока частицы
взаимодействуют между собой. Число частиц определится лишь на второй стадии
взаимодействия, в момент разлета, когда частицы разойдутся настолько, что
перестанут взаимодействовать. Это произойдет тогда, когда энергия системы упадет
до значения, определяемого массой самого легкого адрона − π-мезона
E ~ kTкр ~ mπc2.
В процессе расширения системы отдельные частицы испытывают ускорение,
вызванное эффектом взаимного давления: состояние системы при этом похоже на
жидкое, поэтому Ландау применил законы гидродинамики к системе частиц,
движущихся с релятивистскими скоростями. Теория Ландау получила название
гидродинамической.
Сравним предсказания этих двух теорий о характеристиках множественных
процессов с экспериментальными результатами.
Рассмотрим состав вторичных частиц. Согласно теории Ферми, вторичные частицы
образуются при высокой температуре возбужденной системы, а именно kТ >> mс2, поэтому могут образовываться частицы различной массы, в том числе и нуклоны.
Число частиц различной массы будет определяться только числом возможных
состояний для тех или иных частиц. Например, соотношение числа вторичных нуклонов и пионов должно быть Np
: Nπ = 8 : 3, так как число
возможных состояний для π-мезонов есть 3 (π+, π-, π0), а для нуклонов − 8
(n, р,  , ,
 со спином 1/2 и столько же состояний со спином
-1/2). Однако это
предсказание не согласуется с экспериментом, который дает среди вторичных частиц
80% пионов. со спином 1/2 и столько же состояний со спином
-1/2). Однако это
предсказание не согласуется с экспериментом, который дает среди вторичных частиц
80% пионов.
По теории Ландау система быстро остывает до более низкой температуры
kТкр ~ mπc2, что приводит в основном к образованию пионов, а другие частицы образуются
реже и вылетают по мере остывания системы.
Множественность вторичных частиц теории Ферми и Ландау описывают
одинаково:
n ~ Е1/4.
Эксперимент не согласуется с этим предсказанием. Последние результаты,
полученные на коллайдере в ЦЕРН при энергии 4·1014 эВ, однозначно
аппроксимируются логарифмической зависимостью.
Угловые распределения вторичных частиц по теории Ферми и теории Ландау
различны. Теория Ферми предсказывает изотропное распределение вторичных частиц,
так как в начальной стадии процесса устанавливается равновесие и энергия
равномерно распределяется по степеням свободы. В теории Ландау из-за сильного
взаимодействия между частицами на стадии разлета необходимо рассматривать
уравнения движения жидкости. Поскольку в первый момент объем системы подвержен
релятивистскому сжатию, то расширение носит вначале одномерный характер и
приводит к резко анизотропному распределению вторичных частиц, что согласуется с
экспериментом.
Поперечный импульс
 = psin θ = р*sin θ* зависит от теплового движения частиц в объеме системы. По теории Ферми этот импульс
будет определяться температурой в начальный момент, которая зависит от Е*: Т ~
√Е*. Это означает, что поперечный импульс должен увеличиваться с энергией (рис.
87). = psin θ = р*sin θ* зависит от теплового движения частиц в объеме системы. По теории Ферми этот импульс
будет определяться температурой в начальный момент, которая зависит от Е*: Т ~
√Е*. Это означает, что поперечный импульс должен увеличиваться с энергией (рис.
87).
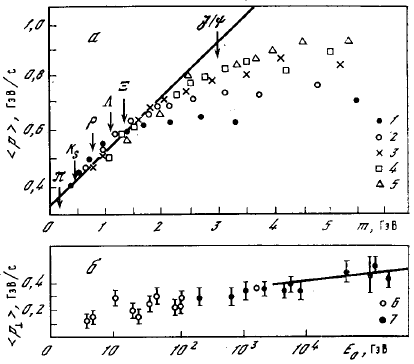
Рис. 87: Зависимость средних поперечных импульсов: а − от массы рождающихся
частиц m (1-5 − 2π, 3π, 4π, 5π, 6π соответственно) и б − от энергии
налетающей частицы (6,7- результаты работ, выполненных на ускорителях и в
космических лучах. Предсказания гидродинамической теории показаны сплошной
линией).
По теории Ландау, как мы видели выше, обмен энергией между частицами системы
продолжается до kТкр ~ mπc2, поэтому поперечный импульс будет определяться
величиной
 * ~ mπc2 и слабо зависеть от энергии взаимодействия. Это
предсказание теории Ландау очень хорошо согласуется с опытом. * ~ mπc2 и слабо зависеть от энергии взаимодействия. Это
предсказание теории Ландау очень хорошо согласуется с опытом.
7.6.2 Мультипериферическая модель
Рассмотренные выше схемы взаимодействий, когда два вступающих в реакцию
адрона передают всю свою энергию в общую систему и сами находятся в этой же
системе, описывают центральное соударение. Но можно представить и другой
механизм взаимодействия: нуклоны не образуют общей системы, а обмениваются
квантами ядерного поля. Наиболее простым является случай, когда обмениваемая
частица − пион. Такие взаимодействия называются периферическими (рис. 88).
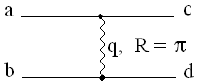
Рис. 88: Диаграмма Фейнмана для периферического соударения. |
Внутренняя линия на
диаграмме соответствует обмену виртуальной частицей с 4-импульсом q, в результате чего
происходит рис. 88: Диаграмма Фейнмана изменение состояний для периферического
соударения. первичных частиц а и b и их превращение в частицы c и d. При этом от частицы а к частице с или от
частицы b к частице d передается 4-импульс
q2 = ( a − a −
 c)2 = ( c)2 = ( b − b −
 d)2. Среди
всех адронов наименьшую массу имеет π-мезон, поэтому обмен пионом наиболее
вероятен. Сложность процесса сильного взаимодействия состоит в том, что обмениваемой частицей могут быть и другие адроны, а также реджеоны. d)2. Среди
всех адронов наименьшую массу имеет π-мезон, поэтому обмен пионом наиболее
вероятен. Сложность процесса сильного взаимодействия состоит в том, что обмениваемой частицей могут быть и другие адроны, а также реджеоны.
Процессы с большой множественностью вторичных частиц можно интерпретировать
как целую цепь пион-пионных или других столкновений, в результате которых
образуются отдельные частицы или пары частиц, или резонансы. Схематически такое
взаимодействие молено представить в виде гребенки (лесенки, мультипериферической
лесенки), где вторичные частицы или группы частиц с 4-импульсами
 i рождаются в
узлах мультипериферической цепочки вместе с виртуальными частицами,
характеризуемыми 4-импульсами qi. i рождаются в
узлах мультипериферической цепочки вместе с виртуальными частицами,
характеризуемыми 4-импульсами qi.
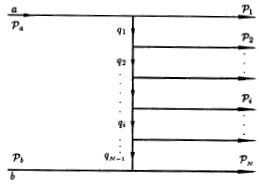
Рис. 89: Мультипериферическая диаграмма процесса множественного рождения. |
Такая диаграмма показана на рис. 89. Здесь адрон а испускает две частицы с 4-импульсами  1 и g1, одна из которых опять испускает две частицы 1 и g1, одна из которых опять испускает две частицы
 2 и
q2 и так далее, пока не
образуется достаточно медленный адрон с 4-импульсом qn-1. Этот медленный адрон
взаимодействует с покоящимся адроном b. 2 и
q2 и так далее, пока не
образуется достаточно медленный адрон с 4-импульсом qn-1. Этот медленный адрон
взаимодействует с покоящимся адроном b.
В основе мультипериферической модели лежит фундаментальный экспериментальный
факт − ограниченность поперечных импульсов (< >
≈ 0.35 ГэВ). Из эксперимента
известно также, что процессы взаимодействия адронов при высоких энергиях
происходят с малыми передачами энергии и импульса между взаимодействующими
частицами. Из этих фактов можно сделать вывод о том, что обмен адронами в
процессе взаимодействия происходит состояниями с небольшими массами, например
пионами, ρ-мезонами и др. В соответствии с принципом неопределенности малые
поперечные импульсы соответствуют большим прицельным параметрам, что и приводит
к понятию периферичности взаимодействия. >
≈ 0.35 ГэВ). Из эксперимента
известно также, что процессы взаимодействия адронов при высоких энергиях
происходят с малыми передачами энергии и импульса между взаимодействующими
частицами. Из этих фактов можно сделать вывод о том, что обмен адронами в
процессе взаимодействия происходит состояниями с небольшими массами, например
пионами, ρ-мезонами и др. В соответствии с принципом неопределенности малые
поперечные импульсы соответствуют большим прицельным параметрам, что и приводит
к понятию периферичности взаимодействия.
При создании мультипериферической модели имелись в виду следующие
постулаты:
1) ограниченность и приблизительное постоянство поперечного импульса  ; ;
2) ограниченность отношения величин продольных импульсов соседних
частиц и независимость этого отношения от первичной энергии:
xi = pi/pi-1 <1;
3) слабая зависимость процесса испускания частиц из данного узла
мультипериферической цепочки от состояний частиц, испускаемых в других узлах. В
предельном случае считается, что испускание частиц в различных узлах происходит
независимо.
Основные выводы мультипериферической модели следующие:
- Вследствие конечности всех xi и ограниченности
 i разность быстрот
частиц, испускаемых в соседних узлах мультипериферической гребенки, не зависит
от первичной энергии: i разность быстрот
частиц, испускаемых в соседних узлах мультипериферической гребенки, не зависит
от первичной энергии:
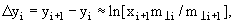
где
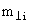 − поперечная масса.
− поперечная масса.
В среднем все интервалы Δуi примерно одинаковы, распределение вторичных
частиц по быстроте будет равномерным:
dN/dy ~ const.
- Множественность определяется числом частиц, испускаемых узлами
мультипериферической гребенки, т.е. dN/dy. Тогда множественность вторичных
частиц логарифмически растет с энергией:
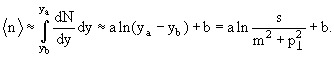
Константа "b" возникает из-за того, что в распределении по быстроте для самых
крайних частиц условие xi = pi/pi-1 <1 не выполняется. Константа
"а" есть
сечение взаимодействия при у* = 0.
На рис. 90 представлены ожидаемые распределения по быстротам при высоких
энергиях в статистической и мультипериферической моделях в лабораторной системе
и системе центра масс.
Область II на рис. 90а, где сечение постоянно, называется центральной или
областью пионизации, I и III − областями фрагментации мишени и налетающей частицы соответственно.
Эксперименты показывают, что, действительно, среди вторичных частиц наблюдаются
частицы различных типов. Основная группа частиц очень многочисленна, импульсы в
СЦМ почти не меняются с увеличением энергии столкновения. Это частицы
пионизации.
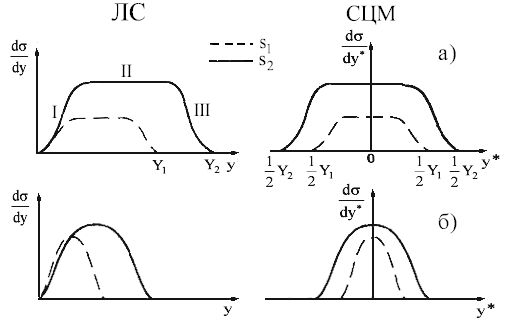
Рис. 90: Распределение по быстротам при энергиях √s1 и √s2 (s1 <
s2):
а − в мультипериферической,
б − в статистической моделях.
Другие частицы имеют импульсы, пропорциональные импульсу налетающей частицы.
Они относятся к области фрагментации налетающей частицы (область III). К этой же
самой области относятся и лидирующие частицы, т.е. частицы, уносящие большую
долю первичной энергии.
К области фрагментации мишени относятся самые медленные в лабораторной
системе частицы (область I).
Распределение по быстроте было получено во многих экспериментах и показано,
что вплоть до энергий 1012 эВ плато в пионизационной области не наблюдается, при этом ширина распределения
растет с ростом энергии. Существование плато означает, что распределение не
зависит от у.
В СЦМ распределение по у* симметрично, и границы изменения у* заключены в
пределах от
−(Y/2) до +(Y/2). На краях распределение не постоянно, а спадает до 0 при
приближении к кинематическому пределу, т.е. является функцией у* − Y/2 в области
III и −у* + Y/2 в области I.
Учитывая, что
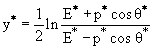
и
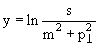
при очень высоких энергиях, когда
 *
>> *
>>
 и Е*
>> mс2 (в
области фрагментации это выполняется при энергии √s > 10 ГэВ), получим и Е*
>> mс2 (в
области фрагментации это выполняется при энергии √s > 10 ГэВ), получим
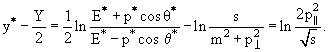
Таким образом, в областях фрагментации сечение есть функция величины
х = 2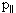 */√s, называемой переменной Фейнмана. Переменную
Фейнмана х можно записать в виде х = */√s, называемой переменной Фейнмана. Переменную
Фейнмана х можно записать в виде х =
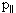 */p*max, где
p*max − максимальный импульс
в СЦМ, тогда видно, что х изменяется от −1 до +1, а области фрагментации в
переменных х будут заключены в пределах */p*max, где
p*max − максимальный импульс
в СЦМ, тогда видно, что х изменяется от −1 до +1, а области фрагментации в
переменных х будут заключены в пределах
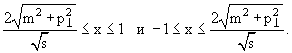
Например, при первичной энергии Е0 = 20 ГэВ х изменяется в пределах от +0.19
до −0.19.
Термин „фрагментация" появился из наглядной картины возникновения нескольких
лидирующих частиц: первичная частица в момент столкновения переходит в
возбужденное состояние, а затем разваливается на фрагменты (адроны). Примером
такого явления может служить образование в
рр-столкновениях барионного
резонанса, который затем распадается на протон и пион, или дифракционная
генерация.
7.6.3 Масштабная инвариантность
Как показывает опыт, многие физические процессы описываются законами,
зависящими лишь от отношения каких-либо величин. Так, число частиц в
электромагнитном ливне при энергии Е гораздо больше критической является
функцией только отношения первичной энергии Е0 к Е и при фиксированном отношении
E0/E не зависит от энергии. Такое свойство физического процесса, когда
уравнения, описывающие этот процесс, не изменяются при одновременном изменении
всех расстояний и отрезков времени в одно и то же число раз, называется масштабной инвариантностью, или
скейлингом.
Так как масса частиц в отсутствие гравитационных возмущений есть величина
постоянная, не зависящая от масштабных преобразований, то для обнаружения
свойства скейлинга необходимы энергии, значительно большие, чем масса самого
тяжелого адрона. В настоящее время известны адроны, имеющие массу ~ 10 ГэВ.
В применении к анализу множественных процессов гипотеза о масштабной инвариантности (скейлинге), была высказана в 1969 году
Р.Фейнманом и Л.Янгом. Они предположили, что структурные функции E(d3σ/dp3)
= f(x, ,s)
при приближении к очень высоким энергиям (или в „асимптотическом пределе") не
должны зависеть от полной энергии столкновения y/s, т.е. должны быть масштабно
инвариантны: ,s)
при приближении к очень высоким энергиям (или в „асимптотическом пределе") не
должны зависеть от полной энергии столкновения y/s, т.е. должны быть масштабно
инвариантны:
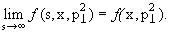 |
(1) |
Это свойство и было названо скейлингом, или автомодельностью.
При скейлинге структурные функции в области фрагментации и в области
пионизации не должны зависеть от энергии, т.е.
ƒ(p,s) = ƒ( ). ).
Поведение сечения в случае скейлинга в зависимости от быстроты у в СЦМ
показано на рис. 91.
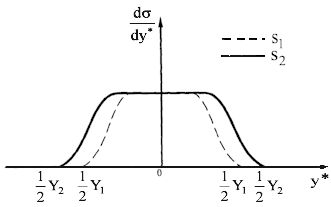
Рис. 91: Распределение по быстроте, ожидаемое в случае скейлинга для энергий
√s1 и √s2 (s1 < s2) в СЦМ.
Для экспериментальной проверки гипотезы скейлинга можно пользоваться
следствиями из формулы (1):
1) рост множественности с энергией должен быть логарифмическим
вследствие логарифмического расширения центральной, пионизационной области
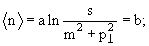
2) средний поперечный импульс ограничен −
< > = const; > = const;
3) средний коэффициент неупругости ограничен −
<K> = const.
Сейчас известно, что до энергий 1012 эВ сечения зависят от s и
масштабно-инвариантное поведение структурных функций не достигается.
В модели предельной фрагментации рассматривается поведение сечений в областях
фрагментации мишени и налетающей частицы при s → ∞. В этих областях в
случае скейлинга сечения также не должны зависеть от энергии. Эксперименты
показывают, что в области фрагментации зависимость сечения от s слабая.
Экспериментальная проверка гипотезы скейлинга является важнейшей задачей
физики высоких энергий.
7.6.4 Введение в квантовую хромодинамику
Эксперименты по глубоко неупругому ер-рассеянию показали, что нуклоны не
являются точечными объектами. Согласно гипотезе, выдвинутой Р.Фейнманом в 60-х
годах, адрон можно рассматривать как систему, состоящую из точечных объектов,
называемых партонами (от английского слова part − часть). В модели иартонов
считается, что адрон участвует во взаимодействиях лишь некоторой своей частью
(партоном), несущей определенную долю 4-импульса адрона. В первом приближении
партоны рассматриваются как точечные частицы, испытывающие только упругие
соударения. Партоны должны обладать специфическими свойствами. Так, партоны
должны существовать в квазисвободном состоянии достаточно долгое время, т.е.
энергия, передаваемая партону при взаимодействии, должна быть настолько велика,
чтобы можно было пренебречь взаимодействием партонов внутри адрона за время
лептон-адронного взаимодействия.
В процессах с небольшой передачей энергии и импульса, например при упругом
ер-рассеянии, партоны себя не проявляют. Это означает, что в этих случаях
происходит когерентное взаимодействие между электроном и протоном.
В 1964 году М.Гелл-Маном и Г.Цвейгом (США) была высказана гипотеза о кварках.
В настоящее время принято, что партоны и кварки тождественны друг другу. В
кварк-партонной модели полагается, что кварки и глюоны и есть партоны.
Сейчас установлено существование шести разновидностей (ароматов) кварков:
u,
d, s, с, b, t. Названия кварков происходят от английских слов up, down, strange,
charm, beauty, truth. Различают токовые и составляющие кварки. Массы токовых
кварков таковы: mu ~ 5 МэВ, md ~ 7 МэВ, ms ~ 150 МэВ,
mс ~ 1.3 ГэВ, mb ~ 4.5 ГэВ, mt > 174 ГэВ.
Свойства кварков представлены в табл. 24. Все кварки имеют спин 1/2.
Таблица 24: Свойства кварков
|
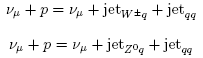

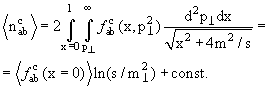
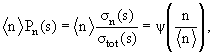



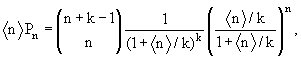


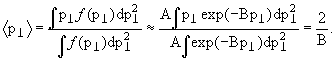
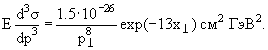



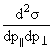 , можно использовать
для изучения процессов фрагментации налетающей частицы. Те же спектры,
рассмотренные в зеркальной (антилабораторной) системе координат, дают сведения о
процессах фрагментации частицы мишени.
, можно использовать
для изучения процессов фрагментации налетающей частицы. Те же спектры,
рассмотренные в зеркальной (антилабораторной) системе координат, дают сведения о
процессах фрагментации частицы мишени.