|
| a + b → c + d + X , или b(a,c)dX или b(a,c). | (3.1) |
Первое обозначение типично для физики элементарных частиц
высоких энергий. Второе типично для ядерной физики или физики низких и
промежуточных энергий. Оно в ряде случаев более информативно; в скобках обычно
указываются: до запятой − снаряд, после запятой − регистрируемые
экспериментатором частицы; перед скобкой указывается частица-мишень, после
скобки − нерегистрируемые частицы, о которых, тем не менее известно, что они
есть в конечном состоянии. Символом X обычно обозначают нерегистрируемую систему
неизвестного числа частиц неизвестного сорта, которая уносит полный 4-импульс
![]() X.
В этом случае
X.
В этом случае
![]() X
называется недостающим импульсом, а величина MX =
X
называется недостающим импульсом, а величина MX =
![]() называется недостающей массой: ведь
называется недостающей массой: ведь
![]() X
находится из закона сохранения энергии-импульса, а не из прямого измерения
4-импульсов входящих в эту систему частиц.
X
находится из закона сохранения энергии-импульса, а не из прямого измерения
4-импульсов входящих в эту систему частиц.
3.1 Классификация реакций рассеяния
Упругое рассеяние. Это − простейшая реакция
рассеяния и частный случай т. н. бинарной
(т. к. и в начальном, и в конечном состоянии имеются лишь 2 частицы) реакции.
При упругом рассеянии в результате столкновения меняются только импульсы и
состояния поляризации частиц, но все другие характеристики (масса, тип) не
меняются. Однако в бинарной неупругой реакции массы и типы частиц в конечном
состоянии иные, чем в начальном (хотя бы для одной из частиц). Квазиупругое
рассеяние. Термин применяется к случаю рассеяния ”более элементарной”
частицы на составной (т. е. "менее элементарной", например, рассеяние протонов
или пионов на ядрах), когда кинематика рассеяния близка к кинематике упругого
рассеяния такой же частицы-снаряда на свободной (не связанной в ядре-мишени)
частице-конституенте мишени; при этом конечное состояние ядра-мишени не
обязательно совпадает с начальным: оно может перейти в одно из своих состояний
дискретного, квазидискретного или непрерывного спектра. Реакции на ядрах с
рождением частиц также часто называются квазисвободными,
если их кинематика близка к кинематике аналогичной реакции на свободной
частице-конституенте мишени. Таким образом, основное отличие квазиупругих
реакций от истинно упругих обусловлено тем, что снаряд рассеивается не на
покоящейся (в л. с.) свободной мишени, а на движущейся (из-за ферми-движения
конституентов в составной системе). При этом необходимо помнить, что масса
свободного конституента отлична от его массы (точнее − величины m2 =
Е2 − p2). когда он находится в составе более сложной
системы в связанном состоянии. Поэтому иногда можно верить в то, что
характеристики "элементарного" взаимодействия можно извлечь из данных о
квазиупругом рассеянии, а иногда − нет: надо специально исследовать, когда
эффектами связи в ядре (т. е. ферми-движением ”элементарной” мишени) или
влиянием окружающей среды на его свойства можно пренебречь.
Фрагментация ядер (или частиц). Это специальный и
достаточно интересный тип столкновений с переходом ядра-мишени в состояния
квази-дискретного типа; возможно также рождение частиц. Интенсивно изучаются
разные классы реакций этого типа, например, т. н. полное разрушение ядра-мишени,
когда освобождаются все нуклоны, или т. н. "мультифрагментация", когда
образуются множество легких ядер-фрагментов, и т. д. Отдельное место занимает
фрагментация легких ядер (например, дейтрона). Она позволяет извлечь информацию
о волновых функциях связанных состояний легчайших ядер. В случае элементарных
частиц к этому же классу относят процессы с рождением частиц, причем те из
образовавшихся частиц, быстроты которых близки к быстроте снаряда или мишени,
называют "фрагментами" снаряда или мишени соответственно.
Множественное рождение частиц. Этот термин обычно
применяется к неупругим реакциям при достаточно высоких энергиях, когда число
рожденных частиц довольно велико: намного больше, чем 2 или 3. В этом случае
число переменных, характеризующих событие, слишком велико для того, чтобы можно
было бы детально проанализировать всю кинематику реакции или даже
зарегистрировать все частицы конечного состояния. С другой стороны, как и в
статистической механике например, появляется возможность применить
статистические подходы и найти специфические для таких реакций закономерности.
Инклюзивные и эксклюзивные типы экспериментов. Термин
появился при изучении процессов множественного рождения. Класс
эксклюзивных экспериментов содержит такие
опыты, в которых регистрируются все частицы-продукты реакции в ее
конечном состоянии, хотя не обязательно, чтобы были измерены все кинематические
характеристики всех частиц. Соответственно, к
инклюзивному типу относят такие эксперименты, в которых
регистрируется несколько (обычно одна-две), но не все частицы-продукты
реакции; зато их кинематические характеристики измеряются настолько полно,
насколько это вообще возможно. В области промежуточных и высоких энергий
основная часть экспериментов последних десятилетий относится к инклюзивному типу.
Легко видеть, что в экспериментах инклюзивного типа
регистрируется некоторый набор элементарных реакций, тогда как в
эксклюзивных экспериментах выделяется одна и только одна элементарная
реакция. Тем не менее, укоренились жаргонные выражения, которые не следует
понимать буквально: "инклюзивная" или "эксклюзивная" реакции.
3.2 Начальные сведения о кинематике
3.2.1 Переменные Мандельстама
Кроме уже рассмотренной ранее переменной s, имеющей смысл
квадрата полной энергии в системе центра масс реакции, одной из важнейших
переменных в физике частиц является переменная t, называемая квадратом
переданного 4-импульса. В случае бинарных реакций есть и третья переменная,
обычно обозначаемая как u; тройка этих переменных, s, t, u взятая вместе,
известна как переменные Мандельстама.
Чтобы яснее представить себе их физический смысл, рассмотрим
бинарную реакцию
| a + b → c + d , или b(a,c)d | (3.2) |
частным случаем которой является упругое рассеяние, когда частицы c и d
тождественны частицам начального состояния a и b, но имеют, вообще говоря,
другие импульсы и энергии, допустимые законом сохранения энергии-импульса. Пусть
![]() i −
4-импульс одной из частиц реакции упругого рассеяния типа (3.2) . Инвариантная
величина s = (
i −
4-импульс одной из частиц реакции упругого рассеяния типа (3.2) . Инвариантная
величина s = (![]() a
+
a
+
![]() b)2
= (
b)2
= (![]() c +
c +
![]() d)2
уже была рассмотрена; ее численное значение не зависит от системы отсчета.
d)2
уже была рассмотрена; ее численное значение не зависит от системы отсчета.
Другой инвариант, то есть не зависящая от выбора системы
отсчета величина, есть t = (![]() a −
a −
![]() c)2.
Она называется квадратом переданного от частицы a системе (b + d)
4-импульса. Очевидно, что с равным успехом ее можно интерпретировать как
квадрат переданного от частицы b системе (a + c)
c)2.
Она называется квадратом переданного от частицы a системе (b + d)
4-импульса. Очевидно, что с равным успехом ее можно интерпретировать как
квадрат переданного от частицы b системе (a + c)
4-импульса, поскольку t = (![]() a −
a −
![]() c)2
= (
c)2
= (![]() b −
b −
![]() d)2.
d)2.
Третий инвариант, который можно построить из
![]() a,
a,
![]() b,
b,
![]() c,
c,
![]() d
есть u = (
d
есть u = (![]() a −
a −
![]() d)2
= (
d)2
= (![]() b −
b −
![]() c)2;
других нетривиальных инвариантов для бинарной реакции нет. Более того, для
бинарной реакции (3.2) даже эти три инварианта не являются независимыми:
c)2;
других нетривиальных инвариантов для бинарной реакции нет. Более того, для
бинарной реакции (3.2) даже эти три инварианта не являются независимыми:
| s + t + u = m2a + m2b + m2c + m2d. | (3.3) |
Внимательно вглядевшись в определения переменных Мандельстама, нетрудно заметить, что все они вытекают из закона сохранения энергии-импульса:
![]() a +
a +
![]() b =
b =
![]() c +
c +
![]() d.
d.
Возведя обе части этого уравнения в квадрат получим
инвариант s. Перенеся
![]() b в
правую часть, а
b в
правую часть, а
![]() c в
левую и возведя обе части полученного уравнения в квадрат, получим инвариант t.
Наконец, если вместо
c в
левую и возведя обе части полученного уравнения в квадрат, получим инвариант t.
Наконец, если вместо
![]() b
перенесем в правую часть
b
перенесем в правую часть
![]() a,
а вместо
a,
а вместо
![]() c в
левую часть перенесем
c в
левую часть перенесем
![]() d и
затем возведем обе части полученного уравнения в квадрат, то получим инвариант
u. Другие подобные преобразования уравнения, представляющего закон сохранения
4-импульса, с переносом только одного 4-вектора из какой-то части в другую,
оставят в одной из частей только один 4-вектор и после возведения в квадрат в
ней появится фиксированное число (т. е. "тривиальный" инвариант), равное
квадрату массы соответствующей частицы.
d и
затем возведем обе части полученного уравнения в квадрат, то получим инвариант
u. Другие подобные преобразования уравнения, представляющего закон сохранения
4-импульса, с переносом только одного 4-вектора из какой-то части в другую,
оставят в одной из частей только один 4-вектор и после возведения в квадрат в
ней появится фиксированное число (т. е. "тривиальный" инвариант), равное
квадрату массы соответствующей частицы.
С точки зрения чистой кинематики, любую реакцию a + b →
+ 2 + 3 + ... + n всегда можно рассматривать как бинарную реакцию (3.2),
представляя себе, например, систему из (n − 1) частиц конечного
состояния как некую одну частицу, например, (2 + 3 +... + n) ≡ X, с
эффективной массой
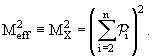
Это нетривиальный инвариант, т. к. его значение нефиксировано и
зависит от сорта частиц в системе X и их 4-импульсов.
Чтобы почувствовать физический смысл переменной Мандельстама
t, обратимся к упругому рассеянию, когда в реакции (3.2) ma
= mc, mb = md. Поскольку величина t
лоренц-инвариантна, вычислим ее в системе центра масс реакции (3.2)
(это удобно, так как в с.ц.м. абсолютная величина импульсов частиц
(и значит, их энергии) при упругом рассеянии не меняется, а меняются
только направления импульсов конечных частиц по отношению к
направлению импульсов начальных). Для упрощения выкладок, когда это
будет удобно, будем считать, что углы рассеяния θ невелики (что не
ограничивает общности рассуждений), так что приближение sinθ и θ
достаточно хорошее. Величины, взятые в с.ц.м., как всегда будем
помечать символом *. Имеем:
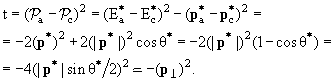 |
(3.4) |
(Здесь стоит напомнить, что поперечный импульс
![]() не меняется при переходе из лабораторной системы в с.ц.м., поэтому в последнем
равенстве формулы (3.4) можно не указывать символ *.)
не меняется при переходе из лабораторной системы в с.ц.м., поэтому в последнем
равенстве формулы (3.4) можно не указывать символ *.)
Из формулы (3.4) видно, что для бинарной реакции (3.2)
переменная Мандельстама | t | есть не что иное, как квадрат переданного
поперечного импульса и она связана с углом рассеяния θ. Вспомнив знаменитое
квантовомеханическое соотношение неопределенности Гейзенберга, легко увидеть,
что величина t характеризует степень пространственного разрешения
деталей структуры объекта, на котором произошло рассеяние, в его поперечном
сечении: чем выше | t |, тем более мелкие структурные неоднородности
могут быть замечены.
Причины, по которым переменные
Мандельстама нашли широчайшее применение в физике частиц, станут ясны позднее;
впрочем, намек на них можно увидеть, если вспомнить курс оптики, а именно −
раздел дифракции.
Из оптики известно, что угловая
зависимость амплитуды световой волны, испытавшей дифракцию на абсолютно черном
диске радиуса R, дается выражением
|
|
(3.5) |
Здесь J1 − функция Бесселя. Имея в виду (3.4), заменим 2ksin θ/2 на √-t и получим
|
|
(3.6) |
Вспомнив, что интенсивность света определяется квадратом амплитуды, видим, что
|
|
(3.7) |
а поскольку dΩ* = dφdcosθ* = dφ2k2dcosθ* /2k2 = dφdt/2k2 (см. (3.4)), то из (3.7) немедленно видим, что
|
|
(3.8) |
Перейдя от углов к мандельстамовской переменной t, получим дифференциальное сечение dσ/dt для дифракционного рассеяния света на абсолютно черном диске
|
|
(3.9) |
Иными словами, зависимость дифференциального сечения (упругого)
рассеяния от квадрата переданного 4-импульса имеет универсальный характер,
независимо от начальной энергии (и того, в какой системе отсчета это сечение
рассматривается) ; его величина определяется только поперечным размером диска,
на котором происходит дифракция. Это не так, если сечение берется в зависимости
от угла рассеяния (см. (3.5)).
Поскольку в микромире все ядра и элементарные частицы
обладают волновыми свойствами, а любая волна на препятствии дифрагирует, то и в
мире ядер, и в мире элементарных частиц существует явление дифракции, а
следовательно, можно ожидать, что представление дифференциальных сечений
упругого рассеяния элементарных частиц в зависимости от переменной Мандельстама
t будет иметь такие же характерные особенности, как и (3.9). И это действительно
имеет место быть.
3.2.2 Пороги реакций.
Законы сохранения энергии и импульса известны всем, кто когда-либо учился в школе и поднялся выше уровня начальных классов (По крайней мере они должны были бы быть известны). Известно также, что он может быть записан в форме
|
|
(3.19) |
где
![]() init − полный 4-импульс начального, а
init − полный 4-импульс начального, а
![]() final − конечного состояний, E и
p −
полные энергия и импульс соответствующих состояний.
final − конечного состояний, E и
p −
полные энергия и импульс соответствующих состояний.
Известно также, что квадрат полной энергии в системе центра масс. т. е.
величина
| s ≡ ( |
(3.11) |
не зависит от системы отсчета (это уже не раз подчеркивалось).
Для системы из нескольких (например, n) частиц часто используется (тоже уже
упомянутое) понятие эффективной массы, определенное как
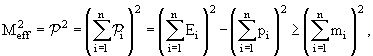 |
(3.12) |
где mi − массы этих частиц. Если n равно числу частиц начального (или
конечного) состояния, то s и
![]() совпадают.
совпадают.
С учетом соотношения (3.12) очевидно, что для рассматриваемой реакции
b(a,c)dX (см. (3.1))
| s ≥ smin ≡ max{(ma + mb), (mc + md + MX)}, | (3.13) |
где smin − минимальное значение величины s, при котором реакция (3.1) еще разрешена законом сохранения энергии-импульса. Оно часто называется просто порогом реакции (3.1). Ясно, что для достижения порога реакции энергия снаряда (в данном случае − частицы a) должна быть не меньше некоторого значения, достаточного для выполнения условий (3.13). Эта энергия называется пороговой энергией; обычно при этом имеют в виду кинетическую энергию Tthresh = Ethresh − ma. Напомним, что обозначение T обычно используется для кинетической энергии, а обозначение E − для полной энергии E = T + m (если иное не оговорено специально).
Кинематика на пороге
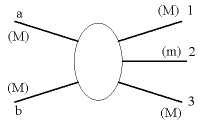 Рис. 3.1. Кинематическая диаграмма для реакции pp → pp + meson как частного случая реакции типа 2 → 3. |
Рассмотрим кинематику реакции 2 → 3 (рис. 3.1).
Возьмем, для примера, неупругую реакцию протон-протонного рассеяния с
рождением мезона, т. е. реакцию pp → pp + meson, и вычислим для нее пороговую
кинетическую энергию Tthresh протонов а также величины t на пороге, имея в виду
передачи 4-импульса от снаряда (projectile) к мезону или к одному из протонов
конечного состояния.
Для нахождения Tthresh достаточно вспомнить определение порога и вычислить
величину s в лабораторной системе отсчета и в системе центра масс, помня о том,
что s есть инвариант относительно лоренцевых преобразований. В результате
нетрудно получить следующие выражения:
| Tthresh =2m (1 + m/4M), tp→p = (pa − p1)2 = -mM, tp→meson = (pa − p2)2 = M2·(1 − 2m/M). |
(3.14) |
Можно обобщить эти формулы на случай реакций типа pA → p+ A' + meson, где A' − не обязательно некоторая связанная система (с точки зрения кинематики, принципиальной разницы между рассматриваемыми частными случаями нет). Главное − освободиться от предположения, что масса мишени b такая же, как снаряда и что частица 3 имеет ту же массу, что и частица 1. Иными словами, будем считать, что все частицы, кроме a и 1, участвующие в процессе типа изображенного на рис. 3.1, имеют разные массы. В результате легко увидеть, что
| Tthresh = MX
+ (MX/Mtarg)·(mproj + MX/2), MX = M3 + m2 − Mtarg, M1 = Ma. |
(3.15) |
Отсюда видно, что чем больше масса мишени, тем меньше порог реакции (при
прочих равных условиях). Величину Mx можно назвать, используя жаргон,
"рожденной" (или "дополнительной") массой (см. также рис. 3.2).
Возьмем частный случай рождения в pp-взаимодействии мезона (или группы
мезонов) в ассоциации с барионом (сюда относятся реакции типа pp → p +Λ+ K+), обозначив массу частицы 3 (бариона) через MY, а массы мезонов (мезона) через mi,
i = 1, .... Тогда можно увидеть, что
 |
(3.16) |
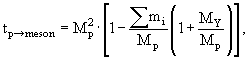 |
(3.17) |
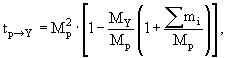 |
(3.18) |
где tp→a, (a = p, Y, meson) есть квадрат переданного между снарядом и
частицей a 4-импульса (см. также рис. 3.3).
Из формул (3.14)-(3.18) видно, что чем "тяжелее" рожденная система, тем выше
(по модулю) передачи 4-импульса. Обычно считается, что при величине передачи
выше ~ 1 ГэВ2/с2 в механизме взаимодействия частиц необходим учет кварковых
степеней свободы элементарных частиц. Т. о. изучение реакций вблизи порога не
обязательно означает работу в области невысоких энергий. (Заметим, что ни на
одном из ускорителей, работавших до запуска Большого Адронного Коллайдера (LHC),
не был достигнут порог образования бозона Хиггса. Иными
словами, физика сверхвысоких (по меркам прошлого века) энергий была даже не
околопороговой, а подпороговой физикой в некотором смысле.)
Область "вблизи порога" в случае pp рассеяния:
| (2M + MX) ≤ spp ≤ (2M + MX + mπ )2. | (3.19) |
"Подпороговая" область для случая pA рассеяния (см. рис. 3.2) есть зона между границами областей, кинематически разрешенных для нуклон-нуклонного (черная кривая на рис. 3.2) и нуклон-ядерного (например, протон-дейтронного или протон-углеродного неупругих взаимодействий на рис. 3.2):
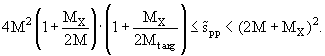 |
(3.20) |
Ширина "подпороговой" области:
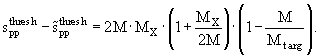 |
(3.21) |
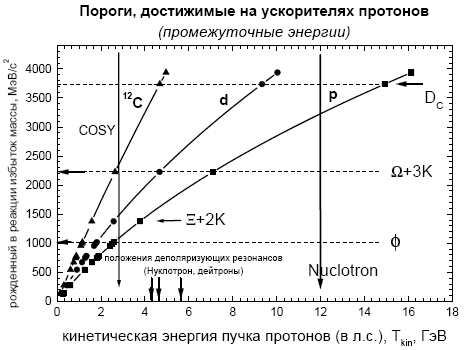
Рис. 3.2. Доступ к порогам рождения частиц в pp, pd и p12C взаимодействиях. Абсцисса: лабораторная кинетическая энергия протонного пучка (для пучков ядер (дейтронов и т. п.) это соответствует кинетической энергии ядра, взятой в расчете на один нуклон). Большими вертикальными стрелками указаны максимальные кинетические энергии протонов для ускорителя COSY (слева) и Нуклотрона (справа). Малые стрелки над осью абсцисс указывают положения слабых деполяризующих резонансов в Нуклотроне для поляризованного d пучка (см. работу [100]). Справа от кривых − кинематически разрешенные области для рождения дополнительной массы (превышение над суммой масс протона-снаряда и мишени, взятой как материальная точка); ее величина отложена на оси ординат; области слева от указанных кривых запрещены законом сохранения энергии-импульса.
Подпороговые реакции интересны тем, что в них можно прощупать как эффекты ферми-движения нуклонов в ядрах, так и эффекты, обусловленные многонуклонными (тесными) корреляциями, поскольку такие реакции кинематически возможны только, если масса "мишени" больше массы свободного нуклона. Грубо говоря, во взаимодействии необходимо участие более одного нуклона (сравните со статистическим описанием плотного газа, когда необходимо учитывать не только парные, но и тройные столкновения атомов (а м. б. и более высокой кратности).
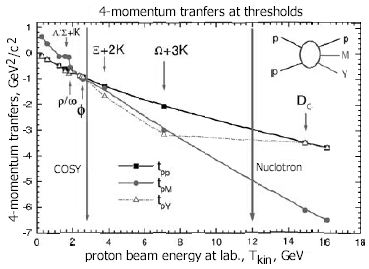
Рис. 3.3. Передачи 4-импульса при рождении частиц на пороге в pp
взаимодействиях.
3.2.3 Относительная скорость
В предыдущей лекции было введено понятие
быстроты и упоминалось понятие
4-скорости частицы с массой m: u =
![]() /m, где
/m, где
![]() − 4-импульс частицы. Вернемся к
этим понятиям снова.
− 4-импульс частицы. Вернемся к
этим понятиям снова.
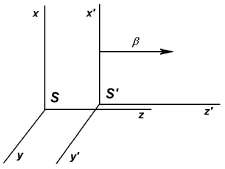 Рис. 3.4. Рис. 3.4. Штрихованная система движется относительно нештрихованной со скоростью β (параллельный перенос). |
Рассмотрим две системы отсчета S и S', причем система S' движется
относительно S с 4-скоростью u = (γ,γβ) параллельно оси Z, т. е. β = (0,0,β). Как всегда, β = v/c, γ = 1/(1 - β2)1/2,
c=1.
В Части I уже напоминалось, что при лоренцевом преобразовании из
нештрихованной системы S (рис. 3.4) в штрихованную, компоненты 4-вектора
![]() =
(A0, A) = (A0,A1,A2,A3) = (A0,Aх,Aу,Az) преобразуются согласно уравнениям
(1.11):
=
(A0, A) = (A0,A1,A2,A3) = (A0,Aх,Aу,Az) преобразуются согласно уравнениям
(1.11):
A'0 = γ(A0
− βA3), A'1 = A1,
A'2 = A2, A'3 = γ(A3
− βA0).
Быстрота ξ (или гиперскорость) была определена в формуле (1.16):
β = tanh ξ, γ = cosh ξ, Γ ≡ β·γ = sinh ξ;
и было показано (формула (1.17), что при двух последовательных переходах из системы S в S' и затем в S", когда система S" движется относительно S' тоже параллельно оси Z, причем скорость системы S' есть β1 (взята в системе S), а системы отсчета S " есть β2 (если она взята в S' и β3, если она взята в S), то в терминах быстрот:
ξ3 = ξ1 + ξ2,
т. е. при последовательно примененных параллельных друг другу преобразованиях
Лоренца быстроты складываются, что не имеет места для скоростей βi. Соответственно, если некоторая физическая величина представлена в зависимости от
быстроты, то форма этой зависимости не зависит от того, взята ли она в системе
центра масс реакции, или в лабораторной системе, или какой-либо другой системы
отсчета.
Оказывается, что с помощью понятия 4-скорости можно не только записать общее
преобразование Лоренца в удобном для практического применения виде, но и
определить релятивистски-инвариантным образом понятие относительной скорости
[30] (здесь и далее, если иное не оговорено специально, речь идет о массивных
частицах).
В самом деле, относительная скорость частиц 1 и 2 и в нерелятивистском случае
определяется как скорость, например, частицы 1, наблюдаемой из системы покоя
частицы 2. Естественно, так же определяется относительная 4-скорость и в
релятивистском случае, причем ясно, что разность 4-скоростей u1 и u2 не есть 4-скорость, т. к. по определению 4-скорости ее квадрат, т. е.
uμuμ, равен
единице: uμuμ = 1. Пусть система покоя частицы 2 будет S', а в исходной системе
S наши частицы имели 4-скорости u1 и u2. Легко убедиться, что 4-скорость
частицы 1 в системе покоя частицы 2, т. е. относительная 4-скорость u12, есть:
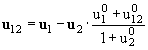 |
(3.22) |
(стоит отметить, что
![]() = E1/m1 = γ1,
u1 = p1/m1 = γ1β1 и т. д.).
= E1/m1 = γ1,
u1 = p1/m1 = γ1β1 и т. д.).
Можно убедиться, что общем случае для 4-вектора А, преобразуемого из системы S в S', когда штрихованная система движется относительно S с 4-скоростью u, преобразование (1.11) можно записать в виде:
| A'0 = (u·A) | (3.23) |
|
|
(3.24) |
(Такая запись во многих случаях весьма удобна; например, именно она используется в стандартной библиотеке программных модулей ЦЕРНа для преобразований Лоренца.)
3.2.4 Инварианты и энергии (импульсы) частиц.
Переменная Мандельстама s имеет, как уже говорилось, смысл полной энергии в системе центра масс сталкивающихся частиц, то есть
| s = ( |
(3.25) |
где звездочка в верхнем индексе, как всегда, помечает кинематические величины в системе центра масс. Кроме того, в системе центра масс pa* = -pb*. Вспоминая, что mi2 = Ei2 − pi2, а также, что
| Еb* = √s − Ea*, | (3.26) |
после возведения в квадрат обеих частей имеем:
|
|
(3.27) |
Импульс p* каждой из частиц a и b в системе центра масс:
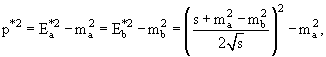 |
(3.28) |
что после честного выполнения всех операций, приводит к выражению
|
|
(3.29) |
где λ(s, ma2, mb2) − знаменитая кинематическая функция, называемая часто треугольной функцией. Понять происхождение (или этимологию) этого термина легко тому, кто помнит школьную формулу Герона для площади треугольника:
| λ(a, b, c) = a2 + b2 + c2 − 2ab − 2bc − 2ac. | (3.30) |
Есть разные формы записи этой функции, их легко получить самостоятельно, но приведенная в (3.30) − наиболее симметричная. Часто встречается и следующая запись:
| λ(a, b, c) = (a − b − c)2 − 4bc. | (3.31) |
Нетрудно убедиться, что импульс p* действителен (как и должно быть в
кинематически разрешенной области), если √s ≥ ma + mb (сравните с (3.13)!), так
как только при этом условии треугольная функция неотрицательна.
Что изменится в отношении формул (3.29) или (3.27), если для бинарной реакции
будет поставлен вопрос об импульсах и энергиях двух частиц конечного состояния c
и d? Легко догадаться, что ровным счетом − ничего, кроме замены масс ma, mb на
массы mc и md. Но разница, все же, может быть. Именно: из (3.29) следует, что
при упругом рассеянии a + b → a' + b' импульс в центре масс реакции не
изменяется, но может повернуться на некоторый угол рассеяния θ*. Поскольку здесь
речь идет о бинарной реакции, все наши векторы лежат в одной и той же плоскости
(![]() *,
*,![]() *), где
*), где
![]() * − поперечный (т. е. перпендикулярный направлению начального
импульса снаряда в л.с.) импульс в см, а
* − поперечный (т. е. перпендикулярный направлению начального
импульса снаряда в л.с.) импульс в см, а
![]() * − продольный импульс рассеянной
частицы (параллельный или антипараллельный направлению начального импульса
снаряда в л.с). В этой плоскости конец вектора p* будет лежать на окружности
радиуса p*.
* − продольный импульс рассеянной
частицы (параллельный или антипараллельный направлению начального импульса
снаряда в л.с). В этой плоскости конец вектора p* будет лежать на окружности
радиуса p*.
Если же случилась неупругая бинарная реакция (mc ≠ ma или mb ≠ md, или
выполнены оба условия) и начальная энергия выше соответствующего порога, то в
с.ц.м. импульс частиц конечного состояния будет на окружности другого радиуса
p*fin ≤ p* (ровно на пороге данной реакции эта окружность вырождается в точку).
3.2.5 Эллипсоид импульсов и его применение
Итак, формула (3.29) определяет на плоскости (![]() *,
*,![]() *) границу кинематически
разрешенной области значений импульсов частиц конечного состояния. Поскольку, с
точки зрения кинематики, любая реакция может быть сведена к бинарной (т. е.
внимание исследователя сосредотачивается на одной из них, например, c, а прочие
группируются в систему с некоторым полным 4-импульсом
*) границу кинематически
разрешенной области значений импульсов частиц конечного состояния. Поскольку, с
точки зрения кинематики, любая реакция может быть сведена к бинарной (т. е.
внимание исследователя сосредотачивается на одной из них, например, c, а прочие
группируются в систему с некоторым полным 4-импульсом
![]() d и эффективной (не
фиксированной!) массой md2 =
d и эффективной (не
фиксированной!) массой md2 =
![]() 2), то 3-импульс выделенной исследователем частицы
c должен всегда быть внутри или на границе этой кинематически разрешенной
области. Как будут выглядеть границы разрешенной законами сохранения области,
если на них посмотрим из лабораторной системы? (В системе центра масс эта
граница, как только что было выяснено, сфера).
2), то 3-импульс выделенной исследователем частицы
c должен всегда быть внутри или на границе этой кинематически разрешенной
области. Как будут выглядеть границы разрешенной законами сохранения области,
если на них посмотрим из лабораторной системы? (В системе центра масс эта
граница, как только что было выяснено, сфера).
Ясно, что параметры преобразований Лоренца (γ и β) для перехода из системы
центра масс в лабораторную (или антилабораторную) тоже можно выразить через
инварианты. Действительно, скорость с.ц.м. есть
|
|
(3.32) |
Итак, мы знаем теперь скорость системы центра масс относительно лабораторной
системы и знаем импульс частицы c конечного состояния реакции. Знаем также, что
вектор импульса частицы c в системе центра масс лежит на окружности радиуса
p*fin, а значение
p*fin можно вычислить согласно (3.29), подставив правильные
значения масс. Примем направление импульса снаряда за направление оси z (система
центра масс, очевидно, движется параллельно этому направлению). Значит, чтобы
найти импульс частицы c в лабораторной системе надо всего лишь сделать
преобразование Лоренца для продольной компоненты импульса
pc*, так как поперечная
компонента этого импульса сохраняется при преобразовании из системы центра масс
в лабораторную. Заметив, что в с.ц.м. граница разрешенной кинематикой области
есть сфера, а продольное преобразование Лоренца деформирует только одну (продольную)
ось координат, видим, что при такой деформации (переходе в лабораторную систему
отсчета) сфера переходит в эллипсоид.
В итоге получаем, что в лабораторной системе отсчета конец вектора импульса
pc частицы c окажется лежащим на некотором эллипсоиде, причем возможно, что этот
эллипсоид выродится в точку, если значение s окажется равным порогу
рассматриваемой реакции, либо же будет лежать на границе кинематически
разрешенной области (тоже эллипсоиде, но максимально возможного размера), если
наша реакция есть просто упругое рассеяние.
Ясно, что малая полуось эллипсоида будет определяться величиной
pc*. Осталось
найти его большую полуось и положение центра. Заметим, что ориентация вектора
поперечного импульса
![]() несущественна, а существенными переменными являются его
модуль и продольный импульс. Поэтому нашу задачу можно рассматривать на
двумерной плоскости (
несущественна, а существенными переменными являются его
модуль и продольный импульс. Поэтому нашу задачу можно рассматривать на
двумерной плоскости (![]() ,pz) и вместо эллипсоида иметь дело с эллипсом импульсов.
Далее будет использован именно этот термин.
,pz) и вместо эллипсоида иметь дело с эллипсом импульсов.
Далее будет использован именно этот термин.
Вспоминая преобразования Лоренца, имеем (здесь p* ≡ pc*):
|
pz = γcmpz* + γcmβcmE*, E = γcmE* + γcmβcmpz*, |
(3.33) |
причем
| ( |
(3.34) |
Второе соотношение из (3.33) можно переписать в виде:
| pz* = pz/γcm − βcmE*, | (3.35) |
после чего, подставив это в (3.34) вместе с первым из соотношений (3.33),
легко получить искомое уравнение эллипса на двумерной плоскости (![]() ,pz):
,pz):
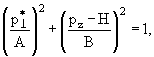 |
(3.36) |
где:
| A = p*, B = γcmp* , H = γcmβcmE*. | (3.37) |
Как видно из (3.35)-(3.37), деформация окружности (3.34) выглядит так: в
продольном направлении она растягивается в γcm раз, не меняя поперечных размеров,
а ее центр сдвигается на величину γcmβcmE*.
Здесь не обойтись без повторения: многие конкретные детали кинематики
конкретной реакции определяются тем, каковы массы начальных и конечных частиц и
каков запас начальной энергии. Подробное обсуждение этих вопросов можно найти в
книгах [1, 2, 3, 4].
Однако есть один важный момент, который необходимо рассмотреть. а именно:
классификация возможных эллипсов (3.36). Она весьма важна при планировании
экспериментов или обсуждении их результатов. Ее знание позволяет как
экспериментаторам, так и теоретикам избежать грубых промахов.
Обозначим скорость нашей частицы, взятую в системе центра масс, через β* =
p*/E*. Рассмотрим два возможных направления импульса рассматриваемой частицы в
с.ц.м.: когда
p* = (![]() * = 0, p*z = -p*) и когда
p* = (
* = 0, p*z = -p*) и когда
p* = (![]() * = 0, p*z = p*). После
преобразования в лабораторную систему получим:
* = 0, p*z = p*). После
преобразования в лабораторную систему получим:
| p1 = (0, γсmE*(βсm − β*)) , p2 = (0, γсmE*(βсm + β*)). | (3.38) |
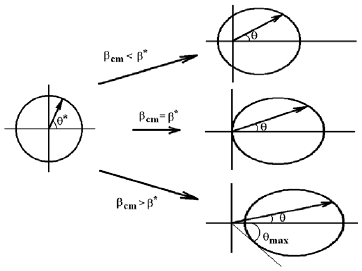
Рис. 3.5. Классификация эллипсов импульсов.
Очевидно, что p1 и p2 есть минимальный pmin и максимальный pmах импульсы частицы в лабораторной системе, причем есть 3 возможных случая (рис. 3.5):
- βсm <β*: в лабораторной системе направление импульса pmin частицы противоположно направлению импульса снаряда (т. е. частица в л.с. летит "назад", под углом 180°);
- βcm = β*: pmin = 0, т. е. частица оказывается в покое относительно лабораторной системы;
- βcm >β*: в лабораторной системе направление импульса pmin частицы совпадает с направлением импульса снаряда (т. е. частица в л.с. летит "вперед", под углом 0°).
Как видно из рис. 3.5, во втором и третьем случаях существует ограничение на
максимальный угол между импульсом частицы и направлением оси Z лабораторной
системы отсчета: в случае 2) этот угол не более 90°, а в случае 3) меньше 90°,
причем для любого угла θ< θmax есть два возможных значения импульса частицы.
Выразим, например, энергию в с.ц.м. через продольный импульс и энергию в л.с,
т. е. выпишем соотношение, обратное последнему выражению из (3.33):
| E* = -γcm βcm p cosθ + γcmE , pz = p cos θ. | (3.39) |
Оно поможет нам связать модуль лабораторного импульса, т. е. величину p, с инвариантами и углом рассеяния, что в свою очередь помогает понять рис. 3.5. В самом деле, из (3.39) имеем:
| E* + βcm γcm p cosθ = γcm(p2 + m2)1/2 . | (3.40) |
Это соотношение можно рассматривать как уравнение для p(θ).
Решение можно записать в следующем виде p± обозначает два решения уравнения
(3.40)):
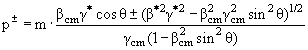 |
3.41 |
или, что то же самое,
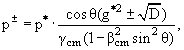 |
3.42 |
|
|
3.43 |
где
| g* = βcm/β*. | (3.44) |
Нетрудно получить формулы и для энергии Е± = ((p±)2 +
m2)1/2.
Отметим, что D = 0 отвечает случаю g* =1, или β* = βcm; тогда p+ = p−. При
g* < 1 величина p− (модуль импульса!!) оказывается отрицательной, т. е.
нефизической, и смысл имеет только решение p+. При g* > 1 оба решения, p− и p+ имеют смысл. Можно показать, что в этом случае максимальный возможный угол
рассеяния определяется соотношением
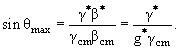 |
3.45 |
Наконец, можно связать и углы рассеяния в с.ц.м. и в лабораторной системе. Ответ имеет вид
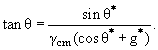 |
3.46 |
3.2.6 Представление о кумулятивных процессах
Рассмотрим кинематику рождения одного пиона в нуклон-нуклонном и
нуклон-дейтронном неупругом рассеянии.
На рисунке 3.6 показаны предельные эллипсы импульсов пиона для реакций его
рождения в NN и dN взаимодействиях (центры соответствующих эллипсов показаны
синей и красной точками). Полный импульс пиона
![]() , где pL и pT − продольная (на направление импульса снаряда) и поперечная компоненты. Эти
эллипсы ограничивают (из-за сохранения энергии-импульса) возможные значения
импульса пиона, рожденного в указанных реакциях. Темным цветом показана область,
разрешенная кинематикой реакции p + p → p + p + π0. Светло-серым цветом
выделена область, недоступная в этой реакции, но разрешенная кинематикой для
реакции
, где pL и pT − продольная (на направление импульса снаряда) и поперечная компоненты. Эти
эллипсы ограничивают (из-за сохранения энергии-импульса) возможные значения
импульса пиона, рожденного в указанных реакциях. Темным цветом показана область,
разрешенная кинематикой реакции p + p → p + p + π0. Светло-серым цветом
выделена область, недоступная в этой реакции, но разрешенная кинематикой для
реакции
d + p → d + p + π0, когда дейтрон кинематически "работает" как единое целое,
т. е. как точечная (бесструктурная) частица с массой около двух масс нуклона.
Рождение пиона с импульсом, принадлежащим этой области, соответствует
кумулятивному рождению.
Итак, под кумулятивной реакцией, в ее простейшем определении, понимается
рождение частиц в кинематической области, запрещенной законами сохранения
энергии-импульса для свободных "частица-частица" столкновений.
Например, при столкновении частиц с ядрами или ядер с ядрами, под
кумулятивным рождением понимают рождение частиц в кинематической области,
запрещенной для свободных NN-столкновений. (Здесь под "свободными" понимаются столкновения этих частиц в пустоте.)
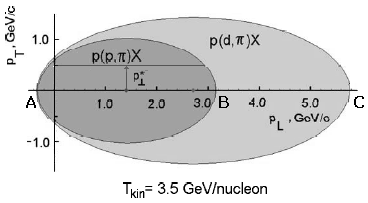
Рис. 3.6. Пример эллипсов импульсов пиона для реакций p(p,π)X и p(d,π)X. Область внутри меньшего эллипса - разрешенная для пиона, рожденного в реакции p(p,π)X (оба нуклона − свободные). Граница большего эллипса соответствует реакции p(d,π)X, когда дейтрон рассматривается как "материальная точка", а эффективная масса системы X минимально возможная (после учета всех законов сохранения и правил отбора). Область импульсов вне большего эллипса − абсолютно запрещена для пиона вследствие законов сохранения энергии и импульса. Между внешним и внутренним эллипсами − ”кумулятивная” область, недоступная для реакции p(p,π)X вследствие тех же законов сохранения энергии и импульса. Однако, она кинематически доступна для реакции p(d,π)X.
В рамках принятого определения, реакции подпорогового рождения частиц на ядрах являются кумулятивными (например, любая неупругая реакция при таких энергиях пучка, когда она попадает в область между кривыми, помеченными метками p и d на рис. 3.2).
3.2.7 Другие "пороги" неупругих реакций
Снова вернемся к теме инвариантов и порогов, но уже под иным углом зрения.
Рассмотрим снова реакцию типа 2 → 2, когда, например, при рассеянии "вперед" частица-мишень превращается в другую, с большей массой. С точки зрения
кинематики это процесс типа µ + m → µ + M, где µ − масса снаряда, m − масса
мишени, M − масса частицы, в которую после рассеяния превратилась частица-мишень.
Имея в виду материал предыдущих разделов, легко догадаться, что если даже
энергия снаряда много выше обычного порога такой реакции, все же есть другой "порог",
а именно: передача 4-импульса в такой реакции должна быть (по модулю) не низке
некоторой пороговой величины | tmin | (напомним, что для упругого рассеяния
такая величина тоже есть и численно она равна нулю). Найдите соответствующую
формулу самостоятельно (задача 20).