|
 |
 |
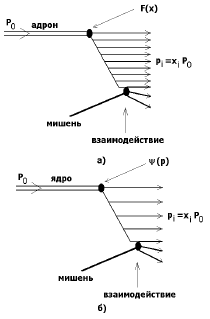
| Рис. 4.1. Фрагментация адронов (а) или релятивистских ядер (б) в партонной (спектаторной) картине соответственно. Поперечный импульс партонов считается малым, взаимодействием партонов (одного и того же адрона) между собой можно пренебречь. | Рис. 4.2. Фрагментация релятивистских дейтронов в партонной картине и основная идея релятивистской динамики на световом фронте. |
Поясним основную идею этого формализма на примере
свободной частицы, движущейся в направлении оси Z в плоскости (t, x = 0, y = 0,
z) так, что в момент времени t = 0 ее координата в пространстве-времени есть
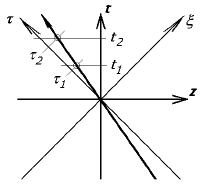
(0,0,0,0). Мировая линия этой частицы изображается на плоскости (t,z) прямой
линией (см. рис. 4.2), лежащей внутри светового конуса, изображенного на рис.
4.2 двумя прямыми, идущими под углами ±45° к оси Z. Как известно, чем ближе
скорость такой частицы к скорости света, тем ближе ее мировая линия к
соответствующей границе светового конуса, и наоборот: когда частица покоится, ее
мировая линия совпадает с осью времени t, то есть мировая линия нерелятивистской
частицы близка к оси t.
Если состояние ψ(t1,z1) частицы (ее
волновая функция) известно в момент времени t = t1, то ее состояние
ψ(t2,z2) в момент времени t = t2 можно
получить, подействовав оператором эволюции на
ψ(t1,z1); для бесконечно малых интервалов времени ∆t = t2
− t1 этот оператор эволюции сводится к гамильтониану соответствующей
системы. Другими словами, гамильтониан переводит состояние
ψ(t,z1), заданное на в 4-мерном пространстве-времени на
гиперповерхности t = t1 в состояние
ψ(t+∆t, z2) на гиперповерхности t2 = t1 +∆t.
Когда система движется вдоль оси Z нерелятивистским образом, ее мировая линия
"прижимается"1
к оси времени.
Теперь понятно, что для ультрарелятивистской системы, мировая
линия которой "прижат" к световому конусу2,
эволюцию состояния системы можно рассматривать по аналогии с нерелятивистским
случаем, приняв направление соответствующей образующей светового конуса за ось
времени. Обозначим эти новые координаты (τ, ζ) вместо (t, z) (рис. 4.2) как
|
|
(4.1) |
П.Дирак [35] показал, что описания динамики системы в переменных (t,
r) и (τ, ρ) полностью эквивалентны при условии, что гамильтониан
системы правильно записан в соответствующих переменных. (Здесь обычные
пространственные координаты (x, у, z) обозначены как вектор r = (z,
![]() ), а
соответствующие новые координаты - как вектор ρ = (ζ,
), а
соответствующие новые координаты - как вектор ρ = (ζ,
![]() ).)
В частности, гамильтониан свободно движущейся нерелятивистской частицы
).)
В частности, гамильтониан свободно движущейся нерелятивистской частицы
| H = p2/2m | (4.2) |
для ультрарелятивистской частицы в новых координатах примет вид (например, см. [36])
|
|
(4.3) |
Аналогия между (4.2) и (4.3) очевидна (стоит обратить
внимание на определение величины η и сравнить его с определением быстроты).
Другими словами, для описания ультрарелятивистской системы можно пользоваться
всем аппаратом нерелятивистской квантовой механики3,
если только поперечные (по отношению к направлению движения системы в целом)
импульсы невелики (нерелятивистские). Именно этим и объясняется
привлекательность динамики на световом фронте. Дополнительным приятным моментом
является то, что (при указанных выше условиях) возможна прежняя, известная из
нерелятивистской квантовой механики, классификация состояний составной системы
по собственным значениям оператора углового момента. Дело в том, что оператор
углового момента в новых координатах светового фронта, вообще говоря, теряет
свою простую нерелятивистскую форму; только при
![]() /
/![]() << 1 она почти точно восстанавливается.
<< 1 она почти точно восстанавливается.
Более подробное и глубокое рассмотрение вопросов описания
релятивистских составных систем в динамике на световом фронте выходит за рамки
этих лекций; для первоначального знакомства с ними следует обратиться к
соответствующей литературе и ссылкам в них: [35]-[40], а также [43, 44] и [55]).
4.3 Дейтрон: основные свойства
Дейтерий, и соответственно, его ядро − дейтрон − были
открыты в 1932 г. Юри,
Брикведде
и Морфи. Краткий обзор истории открытия и определения свойств легчайших ядер,
включая дейтрон, дан в книге [32].
Спин дейтрона был определен в результате анализа сверхтонкого
расщепления линий спектра атомов дейтерия. Для определения магнитного момента
дейтрона был использован метод молекулярного и атомного пучков (лежащие в основе
методов поляризации протонов, дейтронов и многих других стабильных ядер). Первые
измерения были сделаны вскоре после открытия дейтерия − уже в в 1933 г. [33]
(Эстерманн и Штерн; 1934 г. Раби, Келлог и Захариас); знак магнитного момента
впервые был определен в 1936 г. (Келлог, Раби и Захариас, см. указанную ссылку).
Величина магнитного момента4
дейтрона (µd
= 0.85742µN) оказалась близкой к сумме магнитных моментов нейтрона (µn
= -1.9130428µN) и протона (µр = 2.79284739µN): µd
≈ µр + µn. Поскольку спин дейтрона равен единице, этот
факт указывает на то, что нуклоны в дейтроне находятся, в основном, в
симметричном триплетном состоянии (относительный орбитальный момент равен нулю).
Отсюда, из-за принципа Паули, следует, что изоспин дейтрона равен нулю.
Безуспешность поисков рождения пионов в реакции d + d → α + π0
(или d(d, απ0)) и тот факт, что
|
|
(4.4) |
(вместе с предположением об изоскалярности альфа-частицы и изоспине 1/2 для
тритона и гелия-3) также говорят об изоскалярности дейтрона.
Квадрупольный момент дейтрона был впервые измерен в 1939 г.
методом молекулярного пучка (Келлог, Раби, Рамзай и Захариас [34]); его отличие
от нуля говорит о несферичности дейтрона и, следовательно, о присутствии
D-состояния в его волновой функции (примеси состояния с относительным
орбитальным моментом 2 в волновой функции дейтрона).
4.4 Развал дейтрона как модель фрагментации адронов.
До появления пучков релятивистских дейтронов с импульсами
около 10 ГэВ/с реакция развала дейтрона использовалась при сравнительно низких
(менее 1 ГэВ) кинетических энергиях и анализировалась, как правило, в терминах
квазиупругого рассеяния, нерелятивистского описания структуры дейтрона и
полурелятивистского подхода к анализу кинематики. Были замечены некоторые
отклонения от теоретических расчетов для сечений, но в целом экспериментальные
данные соответствовали теоретическим ожиданиям. При этом измерения, как правило,
не касались поляризационных характеристик этой реакции.
Новым и плодотворным оказался подход, основанный, с одной
стороны, на идее такого способа использования реакции развала дейтрона, в
котором экспериментальные условия измерений близки к условиям применимости
партонной картины взаимодействия частиц
высоких энергий, а с другой, на идее проведения анализа полученных данных в
рамках т. н. динамики на световом фронте
(см. работы [46, 47, 48]).
|
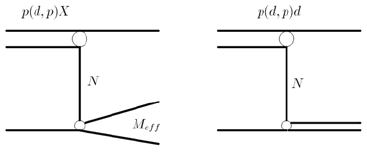
Рис. 4.З. Простейшие (полюсные) диаграммы для процессов развала (фрагментации) дейтронов на протонах и упругого рассеяния d(p,d)p "назад" в с.ц.м. Классификация характерных кинематических областей: упругое обратное рассеяние, развал дейтрона без образования других частиц, развал дейтрона с возможностью рождения других частиц. |
Суть этого подхода (в предельно упрощенном виде) можно
пояснить с помощью полюсных диаграмм, изображенных на рис. 4.3.
Вначале рассмотрим диаграмму, представленную в левой части
рис. 4.3, анализируя ее в духе партонной картины Фейнмана. Именно: примем, что
дейтрон-снаряд состоит всего лишь из двух партонов (нуклонов). По аналогии с
партонной картиной, каждый из этих нуклонов-партонов переносит некоторую долю
полного импульса дейтрона и распределение по импульсам партонов определяется, в
соответствии с квантовой механикой, квадратом волновой функции дейтрона в
импульсном представлении (верхняя вершина рассматриваемой диаграммы). Развал
дейтрона происходит тогда, когда один из нуклонов дейтрона (самый медленный в
л.с.) взаимодействует с покоящейся в л.с. мишенью. Другой нуклон этого
взаимодействия "не замечает", выступая в роли пассивного наблюдателя −
"спектатора". Соответственно, его импульс, измеренный в л.с, остается тем, каким
этот нуклон-партон обладал, находясь в составе начального дейтрона. Если
отобрать такие события, когда поперечные импульсы нуклонов-партонов невелики (в
соответствии с основным положением партонной картины), то есть спектатор
вылетает "вперед", то распределение по уносимому им продольному импульсу будет
определяться квадратом волновой функции дейтрона, если этот импульс больше
половины импульса дейтрона в л.с. (что означает, что взаимодействующий с мишенью
нуклон-партон более медленный в л.с, чем спектатор, в полном соответствии с
партонной картиной). Так как дейтрон релятивистский и рассматривается его
фрагментация в "коллинеарной" кинематике, для вычисления сечений и
поляризационных характеристик реакции следует использовать, как наиболее
адекватный, формализм динамики на световом фронте. В этом случае адекватной
задаче кинематической переменной становится переменная светового фронта
|
|
(4.4) |
где
![]() , Espect
− продольный импульс и полная энергия спектатора, а pd, Ed
− импульс и энергия дейтрона-снаряда (все величины взяты в лабораторной системе
отсчета).
, Espect
− продольный импульс и полная энергия спектатора, а pd, Ed
− импульс и энергия дейтрона-снаряда (все величины взяты в лабораторной системе
отсчета).
Формализм динамики на световом фронте позволяет использовать
в рассматриваемой задаче понятие о нерелятивистской волновой функции дейтрона.
Но здесь не обойтись без хотя бы еще одного (дополнительного) предположения. Оно
касается вопроса о связи между измеряемыми в эксперименте кинематическими
величинами (![]() ,
,
![]() ) и
аргументом волновой функции в импульсном представлении - относительным импульсом
нуклонов в дейтроне k.
) и
аргументом волновой функции в импульсном представлении - относительным импульсом
нуклонов в дейтроне k.
В квантовой механике на световом фронте это предположение
называется предположением о " минимальной релятивизации". Суть его состоит в
том, что (1) с аргументом k волновой функции в импульсном представлении
отождествляется величина
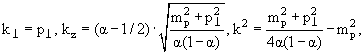 |
(4.4) |
(где принято, что нуклоном-спектатором является протон), а функциональная
зависимость волновой функции от k остается такой же, как в нерелятивистской
квантовой механике; (2) спиновая структура и классификация по орбитальному
угловому моменту для релятивизованной волновой функции при
![]() ~ 0
такая же, как и в нерелятивистской квантовой механике5.
~ 0
такая же, как и в нерелятивистской квантовой механике5.
В схеме "минимальной релятивизации” переменная k имеет смысл
"внутреннего импульса нуклона в дейтроне"; в зависимости от α она меняется от 0
до ∞, как и относительный импульс нуклонов в нерелятивистской квантовой механике.
Величины квадрата переданного от дейтрона к протону 4-импульса t и квадрата
разности 4-скоростей дейтрона и протона также можно выразить через переменную
светового фронта α:
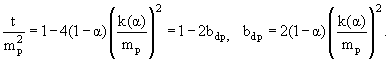
Следует отметить, что в излагаемой схеме во-первых,
пренебрегается энергией связи дейтрона (около 2.2 МэВ), и во-вторых − разницей
масс нейтрона и протона. Тем не менее, используются обозначения mp и
mn, чтобы явно указать, о кинематических характеристиках какого из
нуклонов идет речь.
Вполне возможным является другое предположение, а именно:
отождествление переменной k с модулем вектора импульса протона-спектатора,
взятого в системе покоя дейтрона-снаряда q. Однако наблюдатель, принимающий
такое отождествление, немедленно сталкивается с парадоксом: величина максимально
возможного значения импульса протона-спектатора, взятого в системе покоя
дейтрона-снаряда, ограничена (см. далее) законами сохранения энергии-импульса
величиной
q ≤ qmах = 3mN/4
(mN − масса нуклона), тогда как относительный импульс нуклонов в
дейтроне, согласно нерелятивистской квантовой механике, не ограничен и может
меняться от 0 до ∞. Есть и другие трудности, немедленно возникающие при принятии
этого предположения. Поэтому дальнейшее обсуждение в этом параграфе проводится
на основе гипотезы о "минимальной релятивизации".
Приняв гипотезу "минимальной релятивизации" получим, что для
движущегося относительно лабораторной системы дейтрона с релятивистским
импульсом pd
>> Md, плотность вероятности обнаружить в нем нуклон с внутренним
импульсом k прямо пропорциональна величине
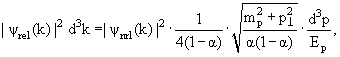 |
(4.7) |
где ψrel (k) − релятивизованная волновая функция дейтрона, ψnrl
(k) − его нерелятивистская волновая функция. Здесь множители в правой части
формулы (4.7) после |ψnrl (k)| есть не что иное, как якобиан перехода
от переменных (kx,ky,kz) к переменным (px,py,pz),
где
p есть вектор импульса протона-спектатора в л.с.
Если бы поведение инвариантного сечения реакции фрагментации
дейтрона в протоны (с небольшим поперечным импульсом) на произвольной мишени в
зависимости от импульса фрагмента (протона) полностью определялось бы диаграммой,
представленной в левой части рис. 4.3, то его можно было бы (приближенно)
записать в виде
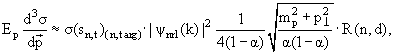 |
(4.8) |
где σ (n, targ) есть сечение взаимодействия медленного нейтрона-партона с мишенью (отвечающее нижней вершине на левой диаграмме рис. 4.3)), а
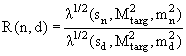 |
(4.9) |
есть отношение Мёллеровских потоков для столкновений дейтрона и
нейтрона-партона с мишенью. Его принято называть "кинематическим фактором". Он
обеспечивает обращение сечения в нуль на кинематической границе а также
учитывает тот факт, что в множитель σ (n, targ) входит, кроме
квадрата матричного элемента взаимодействия медленного нейтрона-партона с
мишенью, Мёллеровский поток нейтрона-партона. Этот поток для свободного нейтрона
иной, чем для нейтрона в составе дейтрона, что следует принять во внимание при
использовании в расчетах экспериментально известного сечения σ(n, targ).
Рассматривая диаграмму Чу-Лоу в разделе VI, мы еще раз встретим отношение типа R
(n,d).
Формула (4.8) приближенная; если бы рассматриваемая диаграмма
рис. 4.3 была бы единственно возможной, то в качестве σ(N,targ)
следовало бы брать полное сечение взаимодействия нейтрона-партона с мишенью
![]() ).
Однако учет глауберовских перерассеяний (т. е. части дополнительных диаграмм)
приводит к тому, что вместо
).
Однако учет глауберовских перерассеяний (т. е. части дополнительных диаграмм)
приводит к тому, что вместо
![]() )
следует брать
)
следует брать
![]() )
полное сечение неупругого взаимодействия (которое примерно в 2 раза меньше),
если только эффективная масса Meff (см. рис. 4.3) заметно выше
суммы масс мишени и нейтрона. Если величина Meff близка к
сумме масс мишени и нейтрона, то есть в конечном состоянии не может быть даже
одного пиона, то вместо σinelаг ) следует брать сечение упругого рассеяния (полное);
если же Meff совпадает с массой дейтрона, то левая диаграмма
рис. 4.3 превращается в правую диаграмму на этом же рисунке, соответствующую
диаграмме однонуклон-ного обмена для упругого рассеяния дейтрона протоном "назад"
в с.ц.м., т. е. реакции p(d,p)d при θ* = 180°. В этом пределе уже нельзя
упрощенно пользоваться такой интегральной характеристикой, как σ(N,targ)
Для нижней вершины рассматриваемой диаграммы, тем более, что она становится
неотличимой от верхней вершины и дифференциальное сечение становится
пропорциональным |ψnrl (k)|4.
)
полное сечение неупругого взаимодействия (которое примерно в 2 раза меньше),
если только эффективная масса Meff (см. рис. 4.3) заметно выше
суммы масс мишени и нейтрона. Если величина Meff близка к
сумме масс мишени и нейтрона, то есть в конечном состоянии не может быть даже
одного пиона, то вместо σinelаг ) следует брать сечение упругого рассеяния (полное);
если же Meff совпадает с массой дейтрона, то левая диаграмма
рис. 4.3 превращается в правую диаграмму на этом же рисунке, соответствующую
диаграмме однонуклон-ного обмена для упругого рассеяния дейтрона протоном "назад"
в с.ц.м., т. е. реакции p(d,p)d при θ* = 180°. В этом пределе уже нельзя
упрощенно пользоваться такой интегральной характеристикой, как σ(N,targ)
Для нижней вершины рассматриваемой диаграммы, тем более, что она становится
неотличимой от верхней вершины и дифференциальное сечение становится
пропорциональным |ψnrl (k)|4.
Таким образом, в реакции развала дейтрона можно выделить
3 характерных области, в которых детальное поведение инвариантных
дифференциальных сечений и поляризационных характеристик реакции может быть
различным, но тем не менее связанным с поведением волновой функции дейтрона в
зависимости от k. Кроме того видно, что может иметь место достаточно тесная
связь между реакцией фрагментации дейтрона в коллинеарной кинематике и упругим
рассеянием дейтрона протоном "назад" в с.ц.м.
Общее поведение инвариантного сечения
фрагментации дейтрона в протоны с вылетом фрагмента под углом 0° по отношению к
импульсу дейтрона-снаряда показано на рис. 4.4. В целом, оно может быть
интерпретировано на основе изложенной схемы и рассчитано согласно формуле (4.8)
с использованием известных волновых функций дейтрона (линии на рисунке 4.4),
хотя при величинах k ~ 200 − 500 МэВ/с эксперимент и теория расходятся даже если
учитываются возможные дополнительные (к рассмотренным простейшим диаграммам) и
более сложные механизмы фрагментации. В области малых |
![]() |
≤ 100 МэВ/с сечение максимально и формула (4.8) дает его неплохое
описание, которое можно еще улучшить, если учесть кулоновские эффекты [51].
|
≤ 100 МэВ/с сечение максимально и формула (4.8) дает его неплохое
описание, которое можно еще улучшить, если учесть кулоновские эффекты [51].
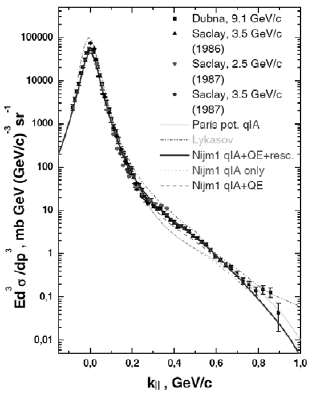
Рис. 4.4. Инвариантное сечение фрагментации на протонной мишени дейтрона в протоны с вылетом фрагмента под углом 0° по отношению к импульсу дейтрона-снаряда в зависимости от продольного импульса к, определенного в тексте. Экспериментальные данные получены в опытах, проведенных в Дубне и Сакле (см. например [45]. [47, 48] и ссылки в этих статьях). Линии − результаты различных теоретических расчетов как в простейшей картине на основе формулы (4.8) (обозначены как квази-импульсное приближение, qIA) так и вкладов других возможных механизмов. В этих расчетах использованы волновые функции дейтрона, полученные на основе современных нуклон-нуклонных потенциалов (Парижского [49] и Ниймегенского [50]).
Сделанный набросок картины фрагментации дейтрона в
коллинеарной кинематике в сильной степени схематичен; ее детализацию можно найти
в оригинальных статьях, но подробное обсуждение этой темы выходит за рамки курса
по основам кинематики. Вполне достаточно было проследить, каким образом основные
черты партонной картина взаимодействия частиц можно физически смоделировать
реакциями фрагментации ядра (в данном случае − дейтрона).
Полезно провести кинематический анализ верхней вершины левой
диаграммы рис. 4.3, где один из нуклонов дейтрона выступает в роли пассивного
наблюдателя − "спектатора".
Выполним его в системе покоя дейтрона и найдем относительный
импульс нейтрона (т. е. импульс, взятый в системе покоя протона-спектатора).
Энергией связи нуклонов в дейтроне пренебрежем из-за ее малости, равно как и
разницей масс протона и нейтрона. Сохраним, однако, обозначения mp и mn, чтобы
иметь возможность различать эти частицы.
В системе покоя дейтрона 4-импульс протона есть
![]() p =
(Ep,q),
p =
(Ep,q),
![]() ,
,
где q ≡ | q |2 и mp - масса протона. Тогда
4-импульс нейтрона, очевидно,
![]() n = (Md −
Ep, -q), эффективная масса системы (нейтрон+протон) есть (
n = (Md −
Ep, -q), эффективная масса системы (нейтрон+протон) есть (![]() p
+
p
+
![]() n)2
= Md2, где Md − масса дейтрона.
n)2
= Md2, где Md − масса дейтрона.
С другой стороны, энергии протона и нейтрона в системе центра
масс нейтрона и протона есть (см. предыдущие лекции):
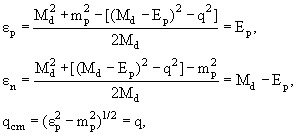
то есть, система центра масс (нейтрон+протон) действительно совпадает с
системой покоя дейтрона.
Найдем теперь относительный импульс нейтрона. Для этого нужно
из системы центра масс (протон+нейтрон), или системы покоя дейтрона, перейти в
систему покоя протона.
4-скорость этой системы есть, очевидно, up = (Ep/mp
, q/mp); тогда преобразование выполнить просто (см. материал
предыдущих лекций):
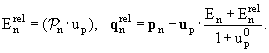 |
(4.10) |
После несложных вычислений, легко получить:
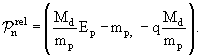 |
(4.11) |
Если теперь потребовать, чтобы нейтрон был "на массовой
поверхности", т. е. чтобы
![]() ,
то легко обнаружить, что относительный импульс нейтрона равен нулю. Это
соответствует ситуации, когда дейтрон разваливается на систему (нейтрон+протон)
и каждый из фрагментов несет (в лабораторной системе отсчета) половину импульса
дейтрона, когда дейтрон движется относительно лабораторной системы.
,
то легко обнаружить, что относительный импульс нейтрона равен нулю. Это
соответствует ситуации, когда дейтрон разваливается на систему (нейтрон+протон)
и каждый из фрагментов несет (в лабораторной системе отсчета) половину импульса
дейтрона, когда дейтрон движется относительно лабораторной системы.
Однако есть и другое условие:
![]() ≥
0. Возможна следующая наглядная (но нестрогая) его трактовка: при
≥
0. Возможна следующая наглядная (но нестрогая) его трактовка: при
![]() = 0 дейтрон вдруг как будто бы "полегчал" на величину mn,
превратившись в пару из протона с импульсом qmax и фиктивной
частицы нулевой массы с импульсом -qmax. Иными словами, почти
вся энергия, запасенная в массе нейтрона, каким-то образом превратилась в
кинетическую энергию протона-"спектатора", но законы сохранения энергии и
импульса не нарушились. Поэтому условие
= 0 дейтрон вдруг как будто бы "полегчал" на величину mn,
превратившись в пару из протона с импульсом qmax и фиктивной
частицы нулевой массы с импульсом -qmax. Иными словами, почти
вся энергия, запасенная в массе нейтрона, каким-то образом превратилась в
кинетическую энергию протона-"спектатора", но законы сохранения энергии и
импульса не нарушились. Поэтому условие
![]() ≥
0 имеет абсолютный характер в том смысле, что если оно нарушается, то говорить о
протоне-спектаторе невозможно: для получения импульса q > qmax, ему
нужно "зачерпнуть" дополнительную энергию из мишени.
≥
0 имеет абсолютный характер в том смысле, что если оно нарушается, то говорить о
протоне-спектаторе невозможно: для получения импульса q > qmax, ему
нужно "зачерпнуть" дополнительную энергию из мишени.
Условие
![]() ≥
0 влечет за собой интересное ограничение на величину относительного импульса:
≥
0 влечет за собой интересное ограничение на величину относительного импульса:
| q ≤ qmax = 3mN/4. | (4.12) |
Это означает, что измеряемый в лабораторной системе импульс
протона-спектатора можно лишь приближенно, при q<< 3mN/4, трактовать
как меру относительного импульса нуклонов в дейтроне "до его развала"; по мере
приближения к этой границе такая трактовка все более и более сомнительна, а
вблизи нее и вовсе неверна. Возникает вопрос: а является ли вообще измеримым
импульсное распределение нуклонов в связанной системе (нейтрон+протон),
задаваемое, согласно нерелятивистской квантовой механике, квадратом модуля
волновой функции дейтрона в импульсном представлении?
Выше была изложена точка зрения, согласно которой на этот
вопрос можно дать утвердительный ответ, если только рассматривать задачу в
рамках "квантовой механики на световом фронте".
4.5 Кинематика глубоконеупругого рассеяния
Обычно, когда говорят о "глубоконеупругом" рассеянии (ГНР), подразумевают неупругое рассеяние лептона на адронной системе, причем такое, когда регистрируемый в конечном состоянии лептон имеет заметно меньшую энергию, чем начальный. В приближении однофотонного обмена такой процесс представляется диаграммой рис. (4.5).
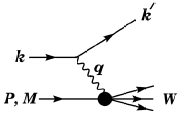
Рис. 4.5. Кинематические переменные для описания глубоконеупругого рассеяния
лептона нуклоном. Величины k, k' − 4-импульсы начального и конечного лептонов,
![]() − 4-импульс
нуклона с массой М. W − масса системы X, получившей отдачу. Обмениваемая частица −
фотон или промежуточный бозон (γ, W±, Z); он переносит к нуклону
4-импульс q = k − k'.
− 4-импульс
нуклона с массой М. W − масса системы X, получившей отдачу. Обмениваемая частица −
фотон или промежуточный бозон (γ, W±, Z); он переносит к нуклону
4-импульс q = k − k'.
Стандартными переменными ГНР являются Q2, v, xBj, y. Поясним эти переменные и рассмотрим интервалы их изменения.
- Потеря энергии лептоном в системе покоя нуклона (поэтому Е, Е' − энергия начального и конечного лептонов берутся в системе покоя нуклона):
| v = q·P/M = Е − Е' ≥ 0. | (4.13) |
- Квадрат передачи 4-импульса:
|
|
(4.14) |
если массами лептонов можно пренебречь, то
| Q2 ≈ 4EE' sin2 (θ/2), | (4.15) |
где θ − угол рассеяния лептона (по отношению к направлению падающего лептона-снаряда). Видно, что с точностью до знака переменная Q2 есть мандельстамовская переменная t; обратный по отношению к t выбор знака величины Q2 обусловлен историческими причинами.
-
x ≈ Q2/(2Mv), (4.16)
эта величина в партонной модели имеет смысл доли импульса нуклона, переносимая партоном.
-
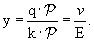
(4.16)
В системе покоя нуклона эта вPличина имеет смысл доли энергии, потерянной лептоном при рассеянии. Из ее определения видно, что это инвариантная переменная.
- Квадрат эффективной массы системы X:
| W2 = ( |
(4.18) |
- Наконец, важной переменной является
|
|
(4.19) |
то есть, квадрат полной энергии лептона и нуклона в системе их центра масс. (Последнее
равенство выписано в л.с.)
Есть еще одна переменная, которую используют, когда вместе с
рассеянным лептоном регистрируется адрон h, входящий в адронную систему с
эффективной массой W в конечном состоянии (рис. 4.5):
| z = Eh/v. | (4.20) |
Здесь Eh − полная энергия регистрируемого адрона. (Передача энергии v адронной системе определена выше.) Смысл переменной z очевиден: это доля переданной энергии, унесенная регистрируемым адроном конечного состояния.
4.5.1 Физический смысл х.
Представим себе, в рамках партонной картины, что
виртуальный бозон (фотон) поглотился партоном, имеющем долю xp
полного 4-импульса нуклона (рассмотрение проведем на световом фронте в
простейшем варианте: т. н. системе бесконечного импульса, в которой
лептон-снаряд имеет бесконечно большой импульс).
Тогда квадрат полной энергии в системе центра масс
виртуального бозона и этого партона равен
|
|
(4.21) |
где m2 − масса партона. Если она много меньше прочих кинематических величин, характерных для задачи, то ею можно пренебречь (равно как и массой нуклона), и в конечном итоге из (4.21) имеем
|
|
(4.22) |
где видно, что xp в формуле (4.21) есть не что иное, как x из
(4.16). При анализе глубоконеупругого рассеяния лептонов эту переменную называют
"Бьеркеновский x ", или xBjorken ≡ xBj.
Кинематически разрешенные области изменения переменных ГНР
схематически изображены на рис. 4.6.
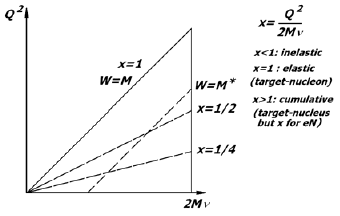
Рис. 4.6. Области изменения кинематических переменных. Здесь 2Mν = Q2/x.
4.5.2 О некоторых терминах
Эффективная масса.
Определение "эффективной массы" в разных областях физики делается различным
образом. Например, есть понятие "эффективной массы" носителей заряда,
употребительное в физике твердого тела и, в частности, в физике полупроводников.
В физике частиц это понятие тоже существует, причем оно определено вполне
однозначно (до той поры, пока речь не идет об элементарных частицах в ядерной
среде): эффективной массой системы n детектируемых частиц называется (или, до
середины 90-х годов называлась) величина
![]() =
( ∑n
=
( ∑n![]() i)2,
где
i)2,
где
![]() i −
4-импульс i-й зарегистрированной частицы, все n частиц были зарегистрированы,
идентифицированы, а их 4-импульс измерен. Это понятие было введено еще на заре
ядерной физики и физики частиц; оно использовалось достаточно долго без
каких-либо затруднений или неоднозначных трактовок. В последние десятилетия оно,
почему-то, стало замещаться бессмысленным термином "инвариантная масса".
i −
4-импульс i-й зарегистрированной частицы, все n частиц были зарегистрированы,
идентифицированы, а их 4-импульс измерен. Это понятие было введено еще на заре
ядерной физики и физики частиц; оно использовалось достаточно долго без
каких-либо затруднений или неоднозначных трактовок. В последние десятилетия оно,
почему-то, стало замещаться бессмысленным термином "инвариантная масса".
Недостающая масса. Как и
эффективная масса, это понятие использовалось без каких-либо затруднений или
неоднозначных трактовок достаточно долго и продолжает использоваться в том же
значении поныне. Оно похоже на понятие эффективной массы, но применяется тогда,
когда не все частицы конечного состояния регистрируются (или не все их импульсы
измеряются). Определение недостающей массы выглядит так:
![]() =
(
=
(![]() beam +
beam +
![]() targ − ∑n
targ − ∑n![]() i)2,
где
i)2,
где
![]() i
имеет тот же смысл, что и выше, a
i
имеет тот же смысл, что и выше, a
![]() beam,
beam,
![]() targ
есть 4-импульсы снаряда и мишени. Иными словами, это не что иное, как
эффективная масса системы не зарегистрированных или ненаблюдаемых частиц.
Можно рассматривать ее (в кинематике) как массу некоторой фиктивной частицы с
полным 4-импульсом
targ
есть 4-импульсы снаряда и мишени. Иными словами, это не что иное, как
эффективная масса системы не зарегистрированных или ненаблюдаемых частиц.
Можно рассматривать ее (в кинематике) как массу некоторой фиктивной частицы с
полным 4-импульсом
![]() miss =
miss =
![]() beam +
beam +
![]() targ − ∑n
targ − ∑n![]() i.
i.
(1) То есть, угол между мировой линией и осью времени очень
мал.
(2) То есть, теперь угол между мировой линией и образующей
светового конуса
(3) Необходимо корректное обращение с гамильтонианом в новых
переменных.
(4) Измеряется в ядерных магнетонах µN =
3.15254166(28)×10-14 МэВ/Тесла.
(5) Дело в том, что в релятивистской теории вопрос о
разделении операторов спина и орбитального углового момента нетривиален. В
динамике на световом фронте это отражается в том, что т. н. оператор
преобразования Мелоша равен единичному оператору только тогда, когда р± =0. Это
обстоятельство забывать не следует.