Применения кинематики (специальные случаи)

Глава 7 Применения кинематики (специальные случаи)

7.1 Критерий Арментероса-Подолянского

Когда физика элементарных частиц еще только появилась и впервые были обнаружены частицы с новым квантовым числом − странностью − инструментарий для регистрации частиц был довольно скуден. Многие из современных детекторов частиц еще не были изобретены. Электронные методы регистрации частиц еще не были широко употребительны, тем более, что и приборов для регистрации и цифровой обработки электронных сигналов было не так уж и много, а те, что были, не могли обеспечить потребности эксперимента.
Известно однако, что "голь на выдумки хитра" и недостаток инструментов восполнялся интеллектом и изобретательностью физиков. Один из примеров такой изобретательности дает критерий, изобретенный для анализа событий распада нейтральных странных частиц: -мезонов и Λ⁰-гиперона, распадающихся преимущественно на пару заряженных частиц.

Отбор событий:

Первичная вершина − и мишени
Вторичная вершина − не ближе, чем> 35 см от первичной (z > 35 cм или
D > σ_D, где D − расстояние).

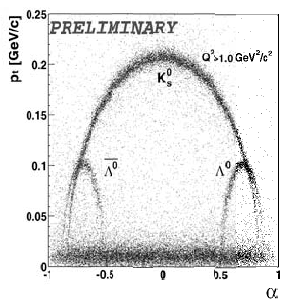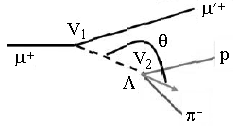
Рис. 7.1. Идентификация событий с рождением Λ⁰, Λ⁰ и частиц методом анализа диаграммы Арментероса-Подолянского [56] в глубоконе-упругом рассеянии мюонов на протонах в эксперименте COMPASS. V₁ − первичная вершина (взаимодействие мюона с протоном), V₂ − вторичная вершина (или вершина распада V⁰-частицы); показана топология события с распадом Λ⁰ или Λ⁰. Видны характерные "арки", соответствующие событиям с рождением и распадом Λ⁰, Λ⁰ и частиц. При отборе событий, включенных в эту диаграмму, требовалось, чтобы направление полного импульса V⁰ " вилки" совпадало с направлением прямой (пунктирная линия), соединяющей вершины V₁и V₂, т. е. угол в между этими направлениями должен быть близок к нулю в некоторых пределах, определяемых угловой точностью измерений.

    В экспериментах по изучению свойств странных частиц нужно было разделить события распада -мезонов и Λ⁰-частиц в условиях, когда измерены импульсы продуктов распада, но сами эти продукты не распознаны (например, известны величина и знак заряда, но не массы). Топология событий распада этих частиц довольно проста: после распада есть две и только две противоположно заряженные частицы: при распаде это − положительно и отрицательно заряженные π-мезоны, а при распаде Л0 - протон и отрицательно заряженный пион. О таких событиях принято было говорить, что они имеют топологию типа V⁰ "вилки", а о распавшейся частице − как о V⁰-частице.
    Для решения этой задачи, когда измерены только заряды и импульсы частиц, образующих V⁰ "вилку", Подолянский и Арментерос [56] предложили в 1954 году изящный и мощный критерий.
   Применение этого критерия основано на кинематическом анализе события распада V⁰-частицы в терминах модуля поперечного (по отношению к направлению движения V⁰-частицы) импульса p_t и некоторой безразмерной переменной

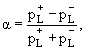
характеризующей асимметрию между продольными (по отношению к тому же направлению) импульсами положительно () и отрицательно () заряженных частиц из этой V⁰ "вилки". Т. о. каждому событию распада V⁰-частицы можно сопоставить некоторую точку на плоскости (α,p_t).
Теперь следует вспомнить об эллипсе импульсов. При двухчастичном распаде V0 в ее системе покоя импульсы продуктов распада одинаковы. Если она распалась так, что в этой системе отсчета угол вылета продуктов распада равен 90°, то при переходе в лабораторную систему поперечный импульс распадных частиц будет равен импульсу распадных частиц в системе покоя. Если же частица V⁰ распалась так, что продукты вылетели под углом 0° или 180° в ее системе покоя, то величины импульсов положительной распадной частицы и отрицательной распадной частицы в лабораторной системе будут определяться соответствующими эллипсами импульсов; эти эллипсы будут разными и относиться к разным типам в классификации эллипсов импульсов, если распадные частицы имеют разные массы (протон и пион) и, соответственно, разные скорости в системе покоя V⁰. Если же распадные частицы одинаковы (два пиона), то и соответствующие эллипсы будут одинаковы. Поэтому разность продольных импульсов распадных частиц в лабораторной системе будет разная, как и величина поперечного импульса (определяемая энерговыделением при распаде) для случаев, когда V⁰ есть нейтральный каон или Λ -гиперон. В результате, распределение событий на плоскости (α, p_t) должно быть разным для разного типа V⁰.
Действительно (см. [56] и рис. 7.1): на плоскости (α,p_t) события распада почти всюду заселяют совершенно другую область, чем события распада Λ⁰, пересекаясь (в идеале) только в одной точке. Из-за конечной точности измерений импульсов эта точка превращается в некоторую область (впрочем, она достаточно невелика).

7.2 Рождение частиц "без отдачи"

    В последнее время оживился интерес к проблеме влияния окружающей ядерной среды на свойства находящихся в ней элементарных частиц, в первую очередь − мезонов.
    Проблема эта не нова: нейтрон в составе атомных ядер стабилен. время жизни Λ-гиперона зависит от атомного номера гипер-ядра. ∆-изобарные возбуждения атомных ядер [58] отличаются по своим характеристикам (положению максимума резонансного пика и его ширине) от ∆-резонанса, возбуждаемого при взаимодействии элементарных частиц в пустоте. Однако по отношению к мезонам однозначного ответа о степени влияния ядерной среды на их свойства пока нет.
    Очевидное условие, выполнение которого экспериментаторы должны обеспечить (или приблизиться, насколько возможно, к нему), состоит в том, что исследуемая частица должна находиться в ядерном окружении как можно дольше (в идеале − всю свою "жизнь"). Иными словами, в идеальном случае она находится в покое относительно ядерной среды, то есть, в реакции рождения она не должна получить импульс (относительно этой среды). Это кинематическое условие называется условием "безотдачности".
    Важность обеспечения условия "безотдачной" кинематики впервые отметил Подгорецкий [60] в применении к проблеме гипер-ядер и создания условий для их образования. Он отметил, что в реакции K + p → π + Λ, где протон покоится в лабораторной системе, при импульсе каонов около
530 МэВ/с Λ-гиперон рождается покоящимся в лаборатории (т.е. относительно протона-мишени). Эта находка стимулировала целое направление исследования гипер-ядер с помощью такой (K,π)-реакции, а найденное им значение импульса каонов стало называться "магическим импульсом" для этой реакции.
    Физическую причину, по которой в ряде случаев возможно выполнение условия "безотдачной" кинематики, легко увидеть, рассмотрев эллипс импульсов для регистрируемой частицы и вспомнив классификацию эллипсов импульсов, рассмотренную в Части II. После этого нетрудно проделать необходимые расчеты для нахождения тех значений импульса пучка, при которых они выполняются.
    Действительно, рассмотрим неупругую реакцию типа b + A → c + A' + d, где b-частица пучка (снаряд), A − мишень (ядро), c − интересующая нас частица, d − выбитый из ядра-мишени фрагмент, A' есть ядро-остаток, практически остающийся в покое в лабораторной системе (спектатор). Если импульс пучка таков, что выполняется условие "безотдачности" для частицы с, то она также будет оставаться в покое в л.с. и ядра-остатка А'. В этой картине элементарной реакцией рождения с для кинематических расчетов является (квазисвободное) взаимодействие снаряда с фрагментом d, входящим в состав ядра-мишени. Для этой-то реакции и нужно найти, при каком импульсе снаряда частица с может не получить импульса отдачи.

Количественно, условие "безотдачности" означает, что для рассматриваемой частицы с ее импульс равен нулю, то есть в соотношении (3.38) имеем

(7.1)

иными словами, скорость рассматриваемой частицы, взятая в центре масс реакции, равна скорости этого центра масс, взятой в лабораторной системе. При этом рожденная частица вылетает "назад" в системе центра масс.
    Рассмотрение эллипса импульсов для частицы с позволяет представить качественную картину эволюции кинематики с изменением импульса снаряда, начиная от порога реакции. Действительно, на пороге все участники реакции в ее конечном состоянии покоятся в центре масс, двигаясь в лабораторной системе вместе, в направлении "вперед". Вместо эллипса ровно на пороге имеем на оси точку: центр будущего эллипса (см. например рис. 3.6). С увеличением импульса снаряда они приобретают все больший импульс в центре масс: появляется эллипс, его полуоси растут а центр, вообще говоря, сдвигается по оси в соответствии с формулами (3.36) и (3.37). Этот эллипс при импульсах снаряда вблизи порога реакции относится к классу, показанному в нижней части рисунка 3.5.
    Если масса частицы с такова, что в системе центра масс ее скорость β_c* никогда не может превзойти скорость самой системы центра масс, то ее эллипс импульсов так и останется в том же классе и условие "безотдачности" никогда не будет выполнено. Так происходит, например, для реакции типа p + p → pp + meson, если рождается мезон с массой m_с > m_р.
    Если же масса частицы с такова, что условие "безотдачности" может быть выполнено, то в момент его выполнения эллипс импульсов частицы с коснется оси и с ростом импульса снаряда перейдет в класс эллипсов, изображенных в верхней части рисунка 3.5.

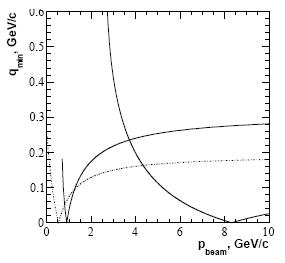
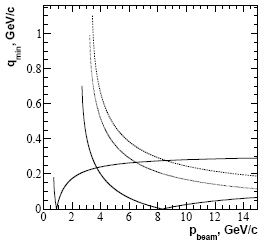
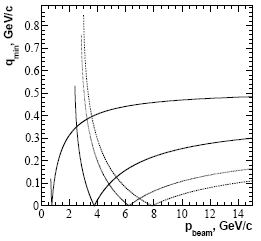
Рис. 7.2. Зависимость минимального импульса (q_min) детектируемой частицы (Λ-гиперона (штрих-пунктирная линия), η- (тонкая сплошная линия) и ω- (жирная сплошная линия) мезонов), рожденной в неупругом рассеянии на протонной мишени, от импульса пучка (р_beam).

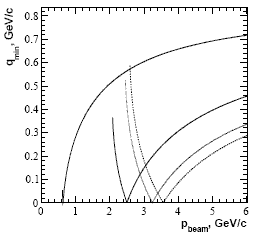Рис. 7.3. Зависимость минимального импульса регистрируемого мезона (η, ω, η' (точечная линия) и

(штриховая линия)), рожденного в неупругом рассеянии на протонной мишени, от импульса пучка (другие обозначения те же, что на рис. 7.2).

Рис. 7.4. Зависимость минимального импульса регистрируемого мезона (те же, что на рис. 7.2), рожденного в неупругом рассеянии на дейтериевой мишени, от импульса пучка, когда дейтрон считается материальной точкой.

Очевидно, что лишь малая часть частиц с, рожденных при импульсе пучка, соответствующем условию "безотдачной" кинематики, действительно будет почти в покое относительно ядра-остатка А'; это та их часть, которая в центре масс "элементарной" реакции квазисвободного рождения движется в с.ц.м. в заднюю полусферу вблизи угла 180°. Основная часть рожденных частиц будет иметь большой импульс.
Минимально возможный импульс частицы с (qmin), легко найти из соотношения (7.1):

q_min ≡ |

| = γ_cmЕ*_c | (β_cm − β*_c) |

(7.2)

    На рис. 7.2 даны зависимости q_min от импульса пучка для реакций p(К,Λ)π (штрих-пунктирная линия), p(π,η)p (тонкая сплошная линия) и p(p,ω)pp (жирная сплошная линия). Видно, как и ожидалось, что чем тяжелее мезон, тем больше импульс пучка, отвечающий выполнению условия "безотдачной" кинематики.
    На рис. 7.3 даны аналогичные графики для реакций p(π,η)p , p (p,ω)pp, p (p,)pp и p (p,η')pp. Видно, что в pp рассеянии для массивных мезонов (η' и ), масса которых больше массы протона, их рождение с нулевым лабораторным импульсом невозможно.
    Поскольку скорость центра масс при фиксированном типе частиц пучка и их импульсе определяется массой мишени, то ее увеличение уменьшает скорость центра масс и даже для тяжелых мезонов могут открыться возможности "безотдачного" образования. В этом можно убедиться и аналитически, в пределе больших s, и численным расчетом. Например, взяв в качестве частицы-мишени дейтрон и считая его материальной точкой (в которой сконцентрирована вся его масса), видим, что для тяжелых мезонов появляются "магические" импульсы (рис. 7.4). Этот предел находится на кинематической границе (см. в качестве примера рис. 3.6, граница большего эллипса). Видно также, что при кумулятивном рождении возможно достижение условия "безотдачности" для мезонов тяжелее протона η' и ) при относительно невысоких лабораторных импульсах.
    Из рисунков 7.5, 7.6, 7.7 можно увидеть, как меняются линии минимального импульса с ростом импульса пучка при разных "коэффициентах кумулятивности", т. е. на разных расстояниях от границы максимально возможной области, разрешенной кинематикой для свободных столкновений "снаряд - нуклон" (см. опять-таки пример рис. 3.6, на этот раз − граница меньшего эллипса).

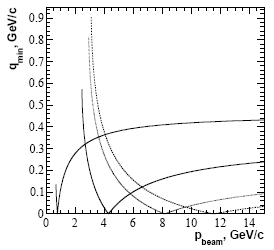
Рис. 7.5. Зависимость минимального импульса тех же мезонов, что на рис. 7.4, при их рождении в кумулятивной области на дейтериевой мишени, от импульса пучка. Масса "эффективной мишени" равна 1.25 × m_р, где m_р − масса протона.


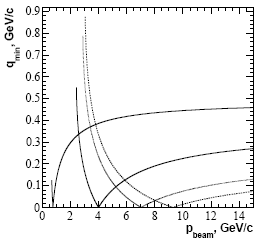
Рис. 7.6. То же, что на предыдущем рисунке, но масса "эффективной мишени" равна 1.30 × m_p	Рис. 7.7. То же, что на предыдущем рисунке, но масса "эффективной мишени" равна 1.35 × m_p

Сравнение скоростей системы центра масс и рожденной частицы

В Части II даны формулы для нахождения импульса и энергии частицы c, рожденной в реакции
b + t → c + X; здесь b − частица-снаряд, t − мишень с массой m_targ, покоящаяся в лабораторной системе, X − ненаблюдаемая система с массой M (недостающая масса):

Там же было упомянуто, что в пределе высоких энергий скорость центра масс дается приближенной формулой

β_cm ≈ 1 − 2m_targ/s

Вспомнив, что β_c* = p_c*/E_c* и рассмотрев предел высоких энергий для этой величины, нетрудно убедиться, что

Эту формулу можно переписать в другом виде:

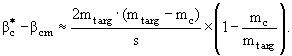
Таким образом, если масса регистрируемой частицы больше массы мишени, знак разности скоростей отрицательный, то есть такой же, как и на пороге, что означает невозможность выполнения условия кинематики "без отдачи". Для обратного случая видно, что знак разности скоростей при высоких энергиях положительный, т.е. при некотором значении импульса снаряда происходит смена знака. Именно при этом значении и выполняется условие "безотдачности".

7.3 Особенности кинематики при фиксированном угле

Так называемая "кинематика фиксированного угла" часто встречается на практике. В этом случае следует иметь в виду, что кинематические переменные, характеризующие процесс неупругого рассеяния, могут оказаться коррелированными, хотя вообще говоря, они таковыми не являются изначально. Поясним сказанное примером неупругого рассеяния дейтронов протонами "вперед" (на угол 0°).

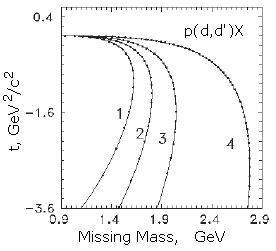
Рис. 7.8. Корреляция (M_X − t) на примере реакции (d,d') с регистрацией рассеянного дейтрона под углом 0°. Линии на плоскости (Mmiss, t) соответствуют изменению переданной мишени энергии Q при фиксированном значении угла вылета регистрируемого дейтрона. Кривые 1, 2, 3, 4 даны для импульсов дейтронного пучка 3.73 ГэВ/с, 4.495 ГэВ/с, 5.532 ГэВ/с и 9.0 ГэВ/с соответственно. Точки на кривых расположены с шагом 100 МэВ по величине Q [57].

При рассеянии на фиксированный угол (в данном примере − "вперед") квадрат переданного 4-импульса t и "недостающая масса" M_X определяются одной и той же величиной: переданной энергией Q = E₀ − E_d' (здесь E₀ − начальная энергия пучка, E_d' − энергия рассеянного дейтрона):

Q = E₀ − E_d'; t = Q² − (p₀ − p_d')²;
M_X = (Q + M_targ)² − (p₀ − p_d')².

(7.3)

Это означает, что меняя переданную энергию, экспериментатор одновременно изменяет и величину t, и величину "недостающей массы" M_X (см. рис. 7.8).

7.4 Кинематика квазиупругого рассеяния

    Как уже упоминалось в Части II, говоря о квазиупругом рассеянии имеют в виду рассеяние "более элементарной" частицы на составной (т. е."менее элементарной", например, рассеяние протонов или пионов на ядрах), когда кинематика рассеяния близка к кинематике упругого рассеяния такой же частицы-снаряда на свободной (не связанной в мишени) частице-конституенте мишени. Конечное состояние частицы-мишени (например, атома или ядра) не обязательно совпадает с начальным. Более того, испытавший отдачу конституент обычно вылетает из частицы-мишени.
    Итак, основное отличие квазиупругих реакций от истинно упругих обусловлено тем, что снаряд рассеивается не на покоящейся (в л.с.) свободной частице-мишени, а на движущейся из-за фермиевского движения конституентов в связанной системе. Более того, будучи связанной в более сложной системе, частица-мишень имеет массу m²_bound = E² − p² отличную от массы соответствующей свободной частицы. Вытекающие отсюда следствия разнообразны; часть из них можно увидеть из двух примеров: рассеяния релятивистских электронов на электронах, связанных в атоме [94] и реакции возбуждения Δ изобар в ядрах (см. обзор [58]).
    Кинематическую диаграмму для рассматриваемых примеров можно представить в общем виде так, как показано на рис. 7.9.

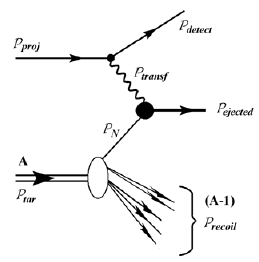
Рис. 7.9. Общая кинематическая диаграмма для квазиупругого рассеяния снаряда с 4-импульсом proj на конституенте составной мишени A с 4-импульсом _tar. Рассеянная частица-снаряд после рассеяния уносит 4-импульс _detect, выбитый конституент приобретает 4-импульс _ejected; 4-импульс оставшейся после вылета конституента (не обязательно связанной) системы (A − 1) обозначен как _recoil. Связанный в частице-мишени конституент до рассеяния на нем снаряда имеет 4-импульс _N.

    При квазиупругом рассеянии электрона на атоме системой A является атом, конституентом − связанный в нем электрон, выбитой из атома частицей является тоже электрон, а системой отдачи
(A − 1) − ион (вообще говоря, возбужденный).
    При возбуждении ∆ изобар в ядрах в реакции типа A(p,n) или A(³He,t) составной системой A является ядро с A нуклонами, выбитой частицей является, например, ∆ изобара, а ядерная система из (A − 1) нуклонов уносит 4-импульс отдачи _recoil (при этом неважно, все ли эти нуклоны связаны или только часть из них, или же в ней вообще нет связанных ядерных фрагментов).
    Поскольку реакция рассматривается в системе отсчета, где мишень покоится (лабораторная система), _tar = (M_A,0).
    Квазиупругое рассеяние электрона на внутриатомном электроне рассматривалось в работе [94] в связи с проблемой измерения поляризации (поляриметрии) пучков релятивистских поляризованных электронов.
    При измерении поляризации пучка необходимо знать анализирующую способность выбранной для поляриметра реакции и измерять лево-правую асимметрию рассеяния, причем важно обеспечить аппаратурную симметрию поляриметра. Обычно эта анализирующая способность зависит от угла рассеяния. При построении поляриметра стремятся максимизировать величину, пропорциональную произведению квадрата анализирующей способности на дифференциальное сечение: она определяет точность измерений и, соответственно, их длительность, необходимую для получения нужной точности знания степени поляризации пучка. В силу разного характера угловой зависимости дифференциального сечения и анализирующей способности, соответствующее произведение имеет, как правило, один максимум при определенном угле рассеяния в системе центра масс. Поэтому вопросы о возможном систематическом отличии углов при квазиупругом рассеянии и аналогичном рассеянии таких же свободных частиц, а также о степени "размытия" угла рассеяния внутренним движением связанного в мишени конституента, достаточно важны. Именно этим вопросам посвящена статья [94].
    Кинематика квазиупругого рождения ∆-изобары на ядре. В этой реакции _N есть 4-импульс внутриядерного нуклона, _ejected − 4-импульс рожденной ∆-изобары. Переданный при столкновении от снаряда системе (мишень+ ∆-изобара) четырех-импульс равен _transf = (v, ∆р)) где v − переданная энергия (или энергия, сброшенная снарядом при неупругом рассеянии), ∆р − переданный 3-импульс (обычный трехмерный вектор).
    Четырех-импульс нуклона, связанного в ядре A, равен _N = _tar − _recoil; его компоненты в лабораторной системе есть

_N = (E_N, p_f) = (M_tar − E_recoil, -p_f) = (M_tar − M_recoil − T_recoil, -p_f),

(7.4)

где p_f − трехмерный импульс ферми-движения нуклона-конституента в ядре-мишени A, M_recoil− масса покоя системы-остатка из (A − 1) нуклонов, Trecoil − ее кинетическая энергия. Обычно ядро-мишень достаточно тяжелое по сравнению с передачей энергии (в л.с.) и поэтому движение системы-остатка можно с хорошей точностью считать нерелятивистским, то есть

T_recoil ≈ p²_f/2M_recoil.

(7.5)

Если состав системы-остатка (A − 1) известен, то масса этой системы также известна, равно как известна и энергия отделения ε_s:

-ε_s = M_tar − (M_recoil + m_N), m_N - ε_s = M_tar − M_recoil,

(7.6)

где m_N есть масса свободного нуклона. Вообще говоря, система-остаток может быть и связанным ядром из (A − 1) нуклонов в каком-то из его возможных состояний, и системой из нескольких ядерных фрагментов. Если состояние системы-остатка регистрируется в конкретном экспериментальном измерении, то все величины в формуле (7.6) относятся к этому состоянию.
Если система-остаток не идентифицируется, то в формуле (7.6) нужно провести усреднение по всему спектру состояний системы-остатка с учетом вероятностей ее конечных состояний; в этом случае в формуле (7.6) под es следует понимать среднюю энергию отделения, а M_recoil как усредненную массу остатка.
Видно, что масса m_N* связанного в ядре нуклона, на котором произошла реакция т. и. квазисвободного рождения (или выбивания) испущенной (ejected) частицы (в рассматриваемом случае − изобары) определяется величиной квадрата его 4-импульса _N

7.7)

и отличается от массы свободного нуклона; это отличие определяется разностью

(7.8)

которая характеризует т. н. "величину схода с массовой поверхности" для этого нуклона. Если испущенной (выбитой) частицей является нуклон, то эта разность будет определять величину почерпнутой у снаряда энергии, необходимой для того, чтобы такое выбивание могло иметь место. Из проведенного рассмотрения следует также, что кинематика такого квазиупругого выбивания будет "размыта" из-за фермиевского движения внутриядерного нуклона (когда же состояние системы-остатка не регистрируется, добавляется дополнительное размытие из-за распределения по величине ε_s).
Масса испущенной (выбитой) частицы M_ejected определяется величиной ²_ejected, которая есть не что иное, как

(7.9)

что можно записать в виде

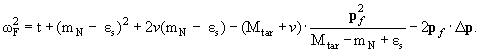(7.10)

Здесь t − мандельстамовская переменная (квадрат переданного от снаряда 4-импульса). Из последнего соотношения видно, что есть еще один источник размывания кинематики квазисвободного выбивания: угол между переданным 3-импульсом и 3-импульсом фермиевского движения нуклона, на котором произошла реакция.
В случае квазиупругого выбивания стабильной частицы (нуклона), величина ω_F фиксирована и равна, очевидно, массе выбитой частицы. Однако в случае, когда эта частица − резонанс (например ∆-изобара), есть еще одна интересная кинематическая особенность.
Дельта-изобара является примером двухчастичного брейт-вигнеровского резонанса R; в этом случае различаются "бегущая масса" ω₁₂ и его "резонансная масса" ω₀, а сечение реакции содержит множитель, отвечающий профилю резонансной линии с учетом ее ширины ΓR распада на систему частиц (1 + 2):

(7.11)

    "Бегущая масса" ω₁₂ является эффективной массой системы частиц (1 + 2), причем обе этих частицы находятся на своих массовых поверхностях. Параметр ширины резонанса, Γ_R(R→ 1 + 2), содержит, в общем случае, фактор (q/q₀)^2l+1. Он вводится в случае резонанса с ненулевым орбитальным моментом движения частиц 1 и 2 в системе их центра масс для учета влияния центробежного барьера на вероятность распада R → (1 + 2) резонанса. Здесь q − импульс частиц 1 и 2 в системе их центра масс при эффективной массе системы (1 + 2) равной ω₁₂, а q₀ − при резонансной массе ω₀.
    В рассматриваемой здесь реакции квазисвободного рождения резонанса обе частицы, входящие в начальное состояние резонирующей системы (1 + 2), находятся вне своих массовых поверхностей: и внутриядерный нуклон с 4-импульсом _N, и виртуальная частица с 4-импульсом _transf, передаваемая от снаряда к этому нуклону (рис. 7.9). Поэтому возникает вопрос о том, правильно ли отождествлять ω₁₂, вычисляемую для частиц 1 и 2 на их массовых поверхностях, с ω_F, когда эти частицы не находятся на своих массовых поверхностях? (Похожий вопрос обсуждался также в работе [59]).
    Оказывается, что нельзя постулировать равенство ω₁₂ = ω_F. Нужно действовать согласно следующему алгоритму:

зная ω_F, найти квадрат "импульса" 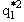частицы 1 (внутриядерного нуклона, например) в системе центра масс частиц 1 и 2, принимая во внимание, что виртуальная частица 2 переносит 4-импульс 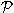_transf и квадрат ее "массы" равен 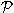²_transf здесь важно также иметь в виду, что величина 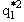не обязана быть положительно определенной:

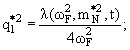(7.12)

вычислить величину √s₁₂, т. е. полную энергию в системе центра масс той же (виртуальной) частицы 2 и реальной (т. е. находящейся на массовой поверхности) частицы 1 с импульсом 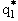в этой системе:
отождествить эту величину с "бегущей" массой резонанса, т. е. приравнять ω₁₂ = √s₁₂, если выполнено условие

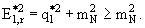
Величина имеет смысл квадрата полной энергии реальной частицы 1 в системе центра масс этой частицы и частицы 2 (виртуальной). Ее нетрудно найти; например, при квазисвободном рождении ∆-изобары частицей 1 является нуклон и для него

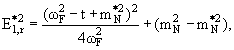(7.13)

где − масса внутриядерного нуклона (см. формулу (7.7)).