|
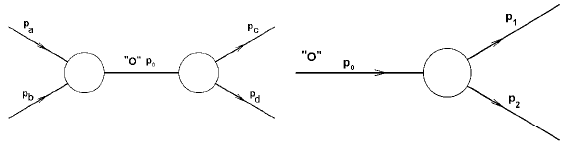
| T0 = M0 − m1 − m2, | (6.1) |
которое много меньше массы M0.
Используя формулы предыдущих лекций с заменой s → M0 нетрудно увидеть, что
|
|
(6.2) |
Иными словами, энергии распадных частиц, почерпнутые из полного энерговыделения, обратно пропорциональны их массам:
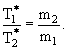
Ясно, что в распаде 0 → 1+2, рассмотренном в системе покоя M0, величины импульсов продуктов распада не зависят от их направления и равны
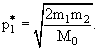 |
(6.3) |
Теперь рассмотрим распад "на лету" и обратим внимание на зависимость импульса распадной частицы от угла ее вылета.
6.2 Углы вылета
Итак, пусть "родительская" частица 0 имеет 4-импульс
![]() 0 = (E0,
p0) (выберем
направление оси Z системы координат по направлению импульса p0). После ее
распада частица-продукт 1 имеет некоторый 4-импульс
0 = (E0,
p0) (выберем
направление оси Z системы координат по направлению импульса p0). После ее
распада частица-продукт 1 имеет некоторый 4-импульс
![]() 1 = (E1,p1). Под углом
вылета распадной частицы будем понимать угол между p1 и направлением оси Z.
Чтобы его найти. вычислим инвариант (
1 = (E1,p1). Под углом
вылета распадной частицы будем понимать угол между p1 и направлением оси Z.
Чтобы его найти. вычислим инвариант (![]() 0 ·
0 ·
![]() 1) в системе покоя распадающейся
частицы и в лабораторной системе:
1) в системе покоя распадающейся
частицы и в лабораторной системе:
|
( |
(6.4) |
Поскольку энергия и импульс распадающейся частицы известны, а энергия распадной частицы связана с ее импульсом и массой, то соотношение (6.4) можно считать уравнением, связывающим импульс распадной частицы с ее углом вылета. Решая это уравнение имеем:
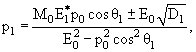 |
(6.5) |
где
|
|
(6.6) |
Решение (6.5) существует, если
|
|
(6.7) |
Полезно поразмыслить над этой формулой, "повертев" ее в руках.
1.
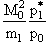 > 1. Тогда возможны любые значения угла вылета (от 0 до 180°), т. е.
угол вылета никак не ограничен.
> 1. Тогда возможны любые значения угла вылета (от 0 до 180°), т. е.
угол вылета никак не ограничен.
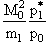 ≤ 1. В этом случае, очевидно, есть ограничение на угол вылета. Если
≤ 1. В этом случае, очевидно, есть ограничение на угол вылета. Если
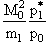 = 1, то он не может быть больше 90°, если же
= 1, то он не может быть больше 90°, если же
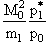 < 1, то есть максимально
возможный (предельный) угол вылета.
< 1, то есть максимально
возможный (предельный) угол вылета.
 |
(6.8) |
Проанализируем эти варианты (результаты полезно сравнить с материалом параграфа 3.2.5).
- Если распадная частица "легкая", например − фотон или нейтрино (т. е. ее масса стремится к нулю или строго равна ему). то угол вылета такой частицы не ограничен (кроме как углом 180°, разумеется). То есть, безмассовая распадная частица всегда может вылететь в направлении, противоположном направлению импульса распадающейся частицы.
- Если распад происходит на частицы, имеющие ненулевую массу, то при любом соотношении между M0 и m1 и, соответственно, любом (но, разумеется, фиксированном!) энерговыделении Tо, всегда найдется такой (большой) импульс pо распадающейся частицы, что продукты распада будут иметь предельный угол вылета. Для этого нужно, чтобы выполнялось условие
|
|
(6.9) |
Иными словами, при достаточно большом начальном импульсе распадающейся частицы все продукты ее распада улетают " вперед". Здесь уместна цитата из книги Копылова [2]: "Причина этого − превосходство в скорости распадающейся частицы над скоростью распадной, взятой в системе покоя распадающейся. Даже если распадная частица летит "назад" в системе покоя распадающейся, последняя летит "вперед" столь стремительно, что продукту распада ничего больше не остается делать, как тоже лететь "вперед"." При этом из (6.9) видно, что чем легче продукт распада, тем выше импульс p0, при котором появляется предельный угол.
- В том же случае распада на частицы, имеющие ненулевую массу, при любом соотношении между Mq и mi и, соответственно, любом фиксированном импульсе pо, многое зависит от энерговыделения: если оно таково, что выполняется условие
|
|
(6.10) |
то продукты распада будут иметь предельный угол вылета.
6.3 Углы разлета
Рассмотрим теперь другую тему, а именно − вопрос об углах разлета распадных частиц все в том же двухчастичном распаде 0 → 1+ 2, понимая под углом разлета ψ(E1) угол между импульсами p1 и p2 при энергии распадной частицы 1 равной E1. Разобраться в этом вопросе поможет эллипс импульсов для распадных частиц (рис. 6.2).
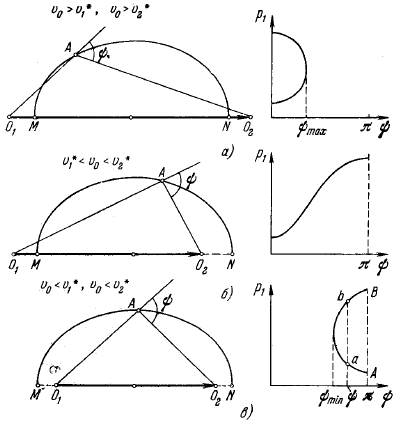
Рис. 6.2. Эллипсы импульсов распадных частиц и пояснение к определению угла разлета (слева); справа − связь между углом разлета и импульсом распадной частицы [2].
Опять воспользуемся инвариантами, на этот раз следующими:
|
|
(6.11) |
Из первого уравнения формулы (6.11) легко получить, выполнив возведение в квадрат и все остальное, что
|
|
(6.12) |
Осталось теперь выразить E2 и p2 через E 1; после необходимых выкладок получим:
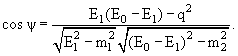 |
(6.13) |
причем предельные значения E1, очевидно, отвечают вылету частицы 1 в системе
покоя 0 "назад"
(E1,min) и "вперед" (E1,max). Соответственно,
|
|
(6.14) |
Большой практический интерес имеет случай распада на два фотона. Стартовав от выписанных в формуле (6.11) инвариантов и замечая, что
|
|
(6.15) |
можно сразу увидеть, что угол разлета фотонов не может быть равным нулю, а затем выразить энергии фотонов через массу распадающейся частицы и ее энергию:
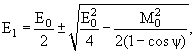 |
(6.16) |
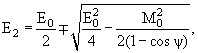 |
(6.17) |
откуда видно, что наименьший угол разлета отвечает симметричной конфигурации, когда
| sin (ψmin/2) = M0/E0 = 1/γ0 | 6.18) |
или
| cos (ψmin/2) = 1/β0, | (6.19) |
поскольку это соответствует обращению в нуль подкоренного выражения в (6.16) и (6.17):
|
|
(6.20) |
Следствия соотношений (6.16)-(6.20):
- с ростом энергии распадающейся частицы угол разлета распадных частиц уменьшается:
- измерение величины минимального угла разлета дает возможность либо измерить энергию распадающейся частицы (если ее масса известна) либо массу (если известна ее энергия).