Глава 9 Сечения и фазовый объем

    В предыдущей главе обсуждалось понятие поперечного сечения реакции и одна из популярных схем его измерения в экспериментах по рассеянию. Было упомянуто, что сечение некоторой реакции связано непосредственно с квадратом модуля амплитуды ее вероятности и размером области в т. н. "фазовом пространстве", в которой могут оказаться конечные продукты реакции. Обсудим здесь эту связь.

9.1 Сечения и матрица рассеяния

    При вычислениях вероятностей переходов в единицу времени используется понятие матрицы рассеяния, или S-матрицы, связывающей начальные (| i >) и конечные (| f >) состояния частиц в рассматриваемом процессе. Она определяется так, что квадрат модуля ее матричного элемента определяет вероятность обнаружения определенного конечного состояния после того, как произошло взаимодействие. Ясно, что матричные элементы S -матрицы могут быть ненулевыми только тогда, когда полный 4-импульс конечного состояния _f  равен полному 4-импульсу начального состояния _i, т. е. выполняется закон сохранения энергии-импульса. Это необходимое (но, очевидно, не достаточное) условие.
    Понятие S-матрицы рассматривалось еще в курсе квантовой механики, поэтому ограничимся здесь кратким напоминанием основных моментов в получении связи между сечением (полным или дифференциальным) реакции < f |←| i > и матричным элементом < f |S| i >. Выделим δ-функцию сохранения 4-импульса в определении ||ичного элемента и перепишем его через "матрицу перехода" T:

< f |S| i > = δf,i + i(2π)4 δ(i-f ) · N · < f |T| i >,

(9.1)

где N − нормировочный множитель, который является, фактически, произведением из  нормировочных множителей волновых функций каждой из частиц, участвующих в реакции (т.е частиц и начального, и конечного состояний). Далее будем считать, что начальные частицы не имеют спина (это упростит запись формул), а начальные и конечные состояния не тождественны.
    Вероятность перехода в единицу времени из состояния | i > в состояние | f > связана с квадратом модуля матричного элемента:

δW/δt = (2π)4 δ(i − f) · |N|2 ·V · | < f |T| i > |2,

(9.2)

где V − нормировочный объем, а при получении выражения (9.2) было использовано соотношение

(9.3)

где одна дельта-функция была заменена интегралом по нормировочному объему и полному времени взаимодействия.
    Вспоминая, как в предыдущей лекции определялось число столкновений нужного типа, видим, что для получения сечения рассматриваемой реакции надо разделить δW/δt на поток падающих частиц и просуммировать по всем конечным состояниям рассматриваемого перехода, что даст

(9.4)

где _n,f  − 4-импульс n-й частицы конечного состояния | f > (то есть, _f  = ∑_nn,f ), и учтено также то обстоятельство, что все регистрируемые частицы находятся на массовой поверхности, т. е.
= . причем полная энергия n-й частицы положительна (поэтому в (9.4) появилась тета-функция).
    Поток падающих частиц (например, взятый в системе покоя частицы-мишени), при нормировке волновых функций "на одну частицу в нормировочном объеме", равен просто отношению относительной скорости начальных частиц на величину нормировочного объема: flux = v₀/V; поэтому (9.4) принимает вид

(9.5)

где относительная скорость v₀ уже обсуждалась раньше и поэтому ее легко выписать:!

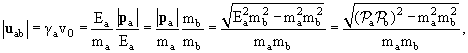
то есть, произведение (см. определение величины InvFlux в (8.3))

есть инвариант. Отсюда видно, что если выбрать нормировочный множитель для начальных частиц a (и b) в виде

(9.7)

то (9.5) примет вид

(9.8)

где N₁ − содержит нормировочные множители только для частиц конечного состояния. Обсудим это выражение.

• Под суммой по конечным состояниям подразумевается:
  • сумма по всем спиновым состояниям;
  • интегрирование по 4-импульсам частиц конечного состояния.
• При интегрировании по всем 4-импульсам имеется в виду инвариантный элемент объема
  d⁴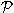_n,f ; однако на самом деле, в силу того, что соответствующая частица находится на массовой поверхности (то есть, 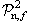= 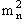) и ее энергия положительна, интегрирование на деле идет по гиперповерхности, выделяемой дельта-функцией. Поэтому вместо четырех переменных в импульсном пространстве только три являются независимыми. В этом легко убедиться, выполнив интегрирование по энергии (см. (9.15)).
• Теперь становится понятным, почему в знаменателе нормировочного множителя в (9.7) появляется энергия.

С учетом сказанного, выражение (9.8) можно переписать как

,

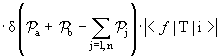(9.9)

Из курса квантовой механики известно, что элемент объема d³p в импульсном пространстве включает (V/(2π)³)d³p состояний, и по ним тоже подразумевается суммирование. Поэтому

,

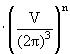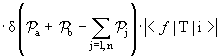(9.10)

Фактически, нормировка одночастичных состояний уже выбрана (с точностью до множителей типа (2π)³) так, что нормировочный объем в (9.10) сокращается с соответствующим знаменателем, спрятанным в |N₁|². В итоге приходим к форме, где нормировочного объема, как и нормировочного множителя, уже нет:

.

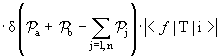(9.11)

    Возможны и другие соглашения о нормировках одночастичных состояний: от этого зависит лишь форма выражения, связывающего матричный элемент реакции с сечением, но не само численное значение сечения. Остается обсудить смысл формулы (9.11).

9.2 Понятие о фазовом объеме

Говоря о состоянии системы n частиц, мы задаем их 4-импульсы. Пространством состояний рассматриваемой системы оказывается, т. о., импульсное пространство. Элемент объема 4-импульсного пространства для системы n частиц (его также называют фазовым пространством для этой системы) есть:

dRn = d41d42...d4n

(9.12)

    Весь доступный рассматриваемым частицам объем этого фазового пространства можно назвать интегралом состояний. Он не бесконечен, поскольку (1) полная энергия системы n частиц фиксирована: (2) 4-импульс каждой из частиц имеет фиксированную "длину", так как
² = E_i² − p_i² = m_i², (говорят, что все эти частицы находятся на "массовой поверхности"). Чтобы учесть эти обстоятельства, элемент фазового объема надо записать в виде

dRn =

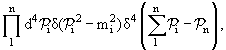(9.13)

где _n − полный 4-импульс нашей системы n частиц.
    Вероятность пребывания нашей системы в той или иной ячейке фазового пространства определяется квадратом модуля амплитуды перехода из начального состояния в интересующее нас конечное (²): умножив его на элемент фазового объема , получаем вероятность dW того, что система будет в соответствующем состоянии:

dW = 2 ·

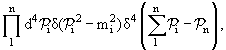(9.14)

и после интегрирования по массовой и энергетической поверхностям (их пересечению) и учета нормировочных факторов, можно получить полную вероятность распада на данные частицы или полное сечение соответствующего процесса, как это было сделано в предыдущем разделе (см. (9.11)).
    Если же зафиксировать энергию E₁ (или модуль импульса) одной из частиц, например, частицы 1, и проинтегрировать по всем остальным переменным, то dR_n можно представить в виде F(E₁)dE₁, где F(E₁) есть "площадь" сечения "физической" части фазового пространства плоскостью E₁ = const; это будет плотность вероятности частице 1 иметь энергию E₁. Проще говоря, это не что иное, как энергетический спектр частицы 1.
    Рассмотрим (гипотетический, но в ряде частных случаев вполне реальный) случай, когда квадрат матричного элемента реакции не зависит от импульсов частиц, иными словами, когда вероятность того, что система окажется в какой-то ячейке фазового пространства, не зависит от положения этой ячейки в фазовом пространстве. Тогда вероятность иметь те или иные численные характеристики системы пропорциональна объему той области фазового пространства, где эти характеристики могут наблюдаться в принципе. Например, полная вероятность реакции или распада будет пропорциональна полному фазовому объему, доступному для данной реакции/распада при данных начальных условиях. То есть, в этом случае подсчет вероятностей сводится к вычислению фазового объема, то есть − кинематике [2]!
    Итак, пусть ² ≡ 1 (или некоторой константе, которую можно положить равной 1, что равносильно изменению единиц измерения). Тогда формула (9.13) определяет элемент фазового объема. Это − 4-мерный скаляр, зависящий только от 4-импульсов, и потому и он, и интеграл от него, не зависят от системы отсчета. Более того, после интегрирования по всем _i он может зависеть только от полного 4-импульса системы и тех инвариантов (скаляров), которые останутся после такого интегрирования. Это означает, что полный фазовый объем должен зависеть только от масс частиц и полной массы системы (или переменной s).
    Заметив, что из четырех компонентов каждого _i только 3 являются независимыми (т. к. частицы находятся на массовой поверхности), можно убрать δ-функции из (9.13), проинтегрировав по четвертой компоненте:

(9.15)

где для перехода к последнему равенству в этой формуле надо использовать известное свойство δ-функции.
    В результате, элемент фазового объема из формы (9.13) принимает форму (уже в пространстве 3-импульсов)

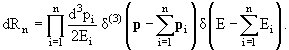(9.16)

    Важно отметить (см. также книгу Бюклинга и Каянти [3]):

1. в формуле (9.16) импульс каждой частицы можно брать в своей особой системе отсчета, проследив за тем, чтобы все импульсы и энергии в аргументах δ-функций были пересчитаны к одной и той же (но безразлично, к какой именно!) системе отсчета:
2. элемент фазового объема, выписанный в (9.16), остается инвариантным.

Итак, фазовый объем системы n частиц есть¹

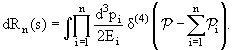(9.17)

    Вычислим его для системы из двух частиц (см. [2]), перейдя, для удобства, в систему их центра масс:

(9.18)

Проинтегрировав по p₂ с учетом δ-функции, получим:

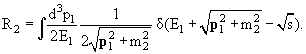(9.19)

    Воспользуемся сферической системой координат: d³p₁ = p₁²dp₁dφd cos θ, где (напомним, что вычисление делается в системе центра масс пары частиц 1 и 2!) все направления вектора p₁ равновероятны, т. е. угол φ меняется равновероятно от 0 до 2π, cos θ меняется равновероятно от -1 до +1 и интегрирование по ним дает просто фактор 4π.
    Интегрирование по p₁ тоже легко выполнить благодаря δ-функции: в самом деле,

p₁²dp₁ = p₁E₁dE₁,
E₂ = ,
x = E₁ + − √s;

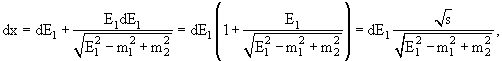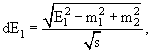(9-20)

то есть.

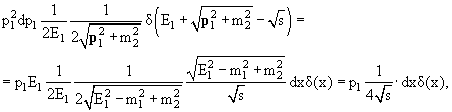(9.21)

где p₁ − импульс частицы 1 в системе центра масс; как известно, это

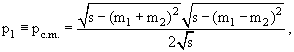(9.22)

    Теперь интеграл по dx берется просто; с учетом фактора 4 π от интегрирования по углам, получаем, что для системы из двух частиц

(9.23)

где восстановлено традиционное обозначение для импульса в системе центра масс p₁* использована также традиционная кинематическая функция λ(a, b, c) = a² + b² + c² − 2ab − 2ac − 2bc.
    Вблизи порога реакции, где √s мало отличается от суммы масс частиц конечного состояния, фазовый объем растет от нуля (который имеет место, когда √s равен пороговому значению) как

(9.24)

(определение переменной ε см. далее), а в ультрарелятивистском пределе (когда всеми массами можно пренебречь)

(9.25)

    Для системы из трех частиц:

(9.26)

и в ультрарелятивистском пределе (m_i → 0)

(9.27)

    Заметим, что в этом пределе

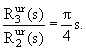(9.28)

    Оказывается, что в общем случае n частиц в ультрарелятивистском пределе

(9.29)

    На практике часто бывает очень полезным знать нерелятивистский предел выражений для фазового объема систем из нескольких частиц. Дело в том, что этот предел возникает при рассмотрении реакции рождения системы из n частиц вблизи ее порога s_thresh, когда При этом полезно использовать обозначение : величину ε часто называют просто "превышением над порогом".

В общем случае n частиц нерелятивистский предел можно получить только приближенно (подробнее см. в книге Г.И.Копылова): соответствующее выражение имеет вид

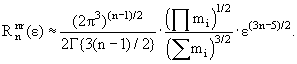(9.30)

    Для системы из трех частиц нерелятивистский предел выглядит так:

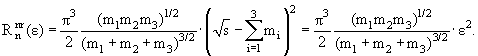(9.31)

    В частности, для реакций типа p + p → p + p + V, где V − мезон,

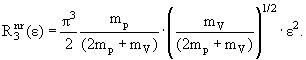(9.32)

    Другими словами, при рождении в такой реакции разных мезонов V₁ и V₂ вблизи их порогов, отношение фазовых объемов (при одинаковом превышении над соответствующими порогами!) есть

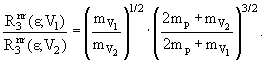(9.33)

Рекуррентное соотношение для фазовых объемов

    Из формулы (9.17) и рис. 10.12 можно заключить, что фазовый объем для n-частичной системы можно выразить через фазовый объем системы с меньшим числом частиц. Действительно, такие соотношения существуют (см. книги [2, 3]). Они достаточно сложны, что можно заметить уже из вычислений для трехчастичного фазового объема.

Примеры из эксперимента

    Рассмотрим реакцию рождения η-мезона в протон-протонных взаимодействиях вблизи порога, задавшись вопросом о том, как повлияет взаимодействие частиц в конечном состоянии (двух протонов и эта-мезона) на энергетическую зависимость полного сечения этой реакции (опять-таки − вблизи порога).

Рис. 9.1. Сплошная кривая: граница кинематически разрешенной области для системы ppη при √s = 2433.8 МэВ (на абсциссе и ординате отложены квадраты эффективных масс пар нуклон-мезон в конечном ppη состоянии). Полный фазовый объем есть площадь фигуры, ограниченной этой замкнутой кривой, т. е. интеграл . Пунктирная кривая − вид такой же границы в случае, если бы протон и η-мезон были бы на 2 МэВ "легче", чем каждый из них в пустоте, см. [65].

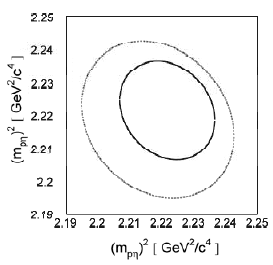    На этот вопрос кинематика может дать ответ, по крайней мере − качественный.
    Действительно, представим себе, что частицы, образовавшись в результате взаимодействия, появились вместе с потенциалами, обеспечивающими их взаимодействие между собой. Покидая область взаимодействия, они (частицы) обладают и некоторой потенциальной энергией, которая либо увеличивает, либо уменьшает их кинетическую энергию, в зависимости от того, каков характер потенциала: притягивательный или отталкивательный.

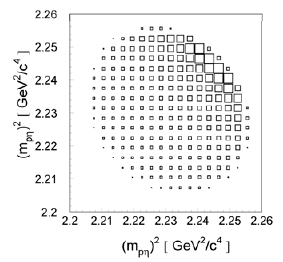Рис. 9.2. Вычисленное распределение событий в фазовом пространстве для системы ррη при превышении над порогом ε = 16 МэВ, искаженное S-волновым протон-протонным взаимодействием в конечном состоянии. Площади квадратов пропорциональны числу событий в соответствующей области. Наибольший квадрат соответствует 260 событиям. См. [65].

   В случае потенциала притяжения, они могут образоваться в тех ячейках фазового пространства, которые недоступны для не взаимодействующих частиц, и затем "втянуты" взаимодействием в конечном состоянии в ту область, которая энергетически разрешена. Это эквивалентно "увеличению" доступного фазового объема и ведет к росту сечения реакции (если бы матричный элемент действительно не зависел бы от кинематических переменных).
    В случае потенциала отталкивания, частицы должны образоваться в меньшей области фазового пространства, так как покидая область взаимодействия, они приобретут дополнительную кинетическую энергию. Таким образом, сечение реакции должно уменьшиться (из-за эффективно меньшего фазового объема) по сравнению с сечением для частиц, не испытывающих взаимодействия в конечном состоянии.
    Эти качественные рассуждения иллюстрируются рис. 9.1; на рис. 9.2 показано, как перераспределяется "заселенность" фазового объема из-за взаимодействия в конечном состоянии.
    Мы вернемся к вопросу о заселенности событиями разных областей фазового пространства позднее, при обсуждении диаграмм Далица.

(1) Здесь, для простоты, сделано переобозначение интеграла по фазовому объему: опущены множители со степенями 2π.