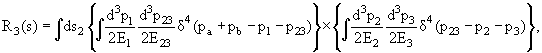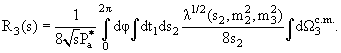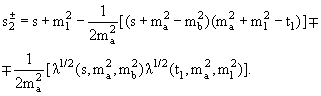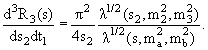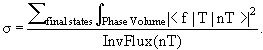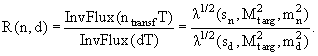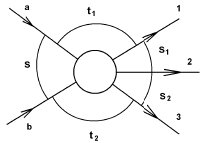
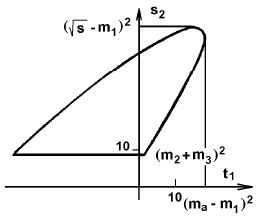
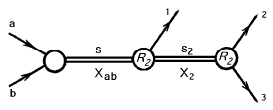
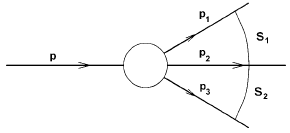Глава 10 Диаграммы Далица и Чу-Лоу

    В неупругих реакциях рассеяния и в реакциях распада с числом частиц в конечном состоянии больше двух, далеко не всю информацию об их механизмах можно извлечь только из одночастичных спектров (т. е. распределений событий в зависимости от кинематических переменных). Большая часть важной информации содержится в коррелированных распределениях, то есть распределениях по кинематическим переменным двух или более частиц. Наиболее наглядный и простой пример дают реакции с тремя частицами в конечном состоянии, рассматриваемые здесь.

10.1 Трехчастичные конечные состояния

10.1.1 Распад 1 → 3

Рис. 10.1. Кинематическая диаграмма для распада одной частицы с 4-импульсом на три (с 4-импульсами 1, 2, 3 соответственно). Иллюстрируется определение переменных s1 и s2 (квадраты эффективных масс систем (1 + 2) и (2 + 3), или, эквивалентно, квадратов полных энергий соответствующих пар частиц в их системах центра масс этих пар).

    Распад P → 1 + 2 + 3, где все частицы − бесспиновые, определяется всего лишь двумя независимыми кинематическим переменными. Действительно, 3 вектора конечного состояния (9 переменных), связаны четырьмя уравнениями сохранения энергии-импульса. Т. к. все частицы − бесспиновые, то начальное состояние изотропно в системе покоя начальной частицы P и конечное состояние не может зависеть от тех углов (3 независимых переменных), которые описывают ориентацию частицы как целого. Поэтому остаются только 9 − 4 − 3 = 2 переменные, которые можно считать независимыми. Их можно выбирать из соображений удобства, предпочитая либо инвариантные, либо неинвариантные переменные.
    Инвариантные переменные. Любая пара инвариантов из приведенного в (10.1) списка может быть выбрана для кинематического описания распада
P → 1+ 2+3 (см. рис. 10.1; s в случае распада реальной частицы есть квадрат ее массы):

s12 ≡ s1 = (1 + 2)2 = ( − 3)2 s23 ≡ s2 = (2 + 3)2 = ( − 1)2 s31 ≡ s3 = (3 + 1)2 = ( − 2)2

(10.1)

Эти инварианты связаны условием:

s1 + s2 + s3 =

(10.2)

10.1.2 Диаграммы Далица

    Для реакции P → 1 + 2 + 3 диаграмму Далица в плоскости (s₁, s₂) можно определить как область, в которой численные значения этих переменных разрешены законами сохранения энергии-импульса (такую область называют физической).
    В более общем смысле под диаграммой Далица понимают физическую область в любых таких переменных, которые связаны с s₁ и s₂ линейно (т. е. якобиан перехода к соответствующим переменным постоянен). Это могут быть, например, любая пара (s_i,s_j): любая пара (E_i*,E_j*); любая пара кинетических энергий (T_i,T_j). (i, j = 1,2,3).
    Уравнение, определяющее границу диаграммы Далица (т. е. границу физической области для перехода P → 1+2+3), можно вывести "напрямую" [3].
    Рассмотрим фазовый объем

R3(s) = 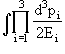δ(p − p1 − p2 − p3)δ(√s − E1 − E2 − E3).

(10.3)

    Проинтегрируем δ-функции. Поскольку фазовый объем инвариантен, можно распорядиться выбором переменных из соображений удобства вычислений.
    Выберем систему покоя распадающейся частицы и проинтегрируем по p₂:

(10.4)

где (опускаем, для краткости, звездочки, указывающие на систему покоя распадающейся частицы, или, что то же самое, систему центра масс (1+2+3)):

(10.5)

Векторы импульсов p₁ и p₃ будем брать в полярной системе координат, то есть, запишем d³p₁ d³p₃ так:

(10.6)

где углы Ω₃ = (cos θ₁₃,φ₃) описывают ориентацию вектора импульса частицы 3 относительно p₁, а углы Ω₁ − ориентацию импульса частицы 1 относительно некоторой оси, пока ее не специфицируя и не интегрируя по Ω₁ и φ₃ (они понадобятся позже).
    Для интегрирования по cos θ₁₃ используем δ-функцию с энергиями, так как dE₂/d cos θ₁₃ = p₁p₃/E_2. В результате:

Здесь Θ − функция ограничивает cos θ₁₃ его физическими значениями. Значения cos θ₁₃ = ±1 соответствуют границе физической области на плоскости (E₁,E₃), то есть, границе диаграммы Далица.
    Теперь можно найти уравнение границы. Его можно получить из (10.5):

(√s − E1 − E3)2 = − + − ± 2[( − )( − )]1/2 + .

(10.8)

или, что то же самое,

(√s − E1 − E3)2 = |p1 ± p3|2 + .

(10.9)

    Можно преобразовать формулу (10.8), возведя в квадрат обе ее части, но при этом будут потеряны сведения об относительных знаках импульсов; тем не менее:

4( − )( − ) = [s + 2E1E3 − 2√s(E1 + E3) + − +  ]2.

(10.10)

    Переменные E₁ и E₃ линейно связаны с s₁ и s₂ (чтобы убедиться в этом, достаточно раскрыть определения (10.1)). Якобиан перехода ∂(E₁,E₂)/∂(s₁,s₂) равен 1/4s. Если теперь перейти в уравнении (10.7) к переменным s1 и s2 и проинтегрировать по телесному углу dΩ₁ (в рассматриваемом распаде нет выделенной оси!), получив 4π, а также учесть, что изменение φ₃ означает всего лишь вращение полной конфигурации импульсов относительно некоторой оси (значит, интегрирование по этой переменной даст всего лишь 2π), то придем к выражению

(−),

(10.11)

где − некоторая функция, зависящая только от кинематических параметров распада и отличная от нуля внутри границы диаграммы Далица.
    Если же проделать то же самое с интегралом в (10.7), то получим

(10.12)

    Из (10.11) или (10.12) видно, что внутри диаграммы Далица плотность распределения вероятности иметь значения независимых переменных (s₁,s₂), или, как принято выражаться, "распределение по фазовому объему" есть константа:

(10.13)

при фиксированном s. Иными словами, все вариации распределения плотности событий (когда каждое событие распада отображается в диаграмме Далица точкой, положение которой задается конфигурацией импульсов и энергий распадных частиц в этом событии) обусловлены динамикой, диктующей зависимость матричного элемента распада от импульсов (или энергий) распадных частиц, а не его кинематикой (в узком смысле). Это одно из важнейших свойств диаграммы Далица.
    Наконец, из уравнения (10.8) можно увидеть еще одно полезное соотношение: на границе диаграммы Далица

(10.14)

10.1.3 Специальные случаи диаграмм Далица

Все массы одинаковы

Рассмотрим событие распада P → 1 + 2 + 3 в системе покоя распадающейся частицы. Будем характеризовать событие кинетическими энергиями частиц: T_i = E_i − m. Массу распадающейся частицы обозначим как M₀ = √s. Очевидно, что выполняется условие

где Q − энерговыделение при распаде. Соотношение (10.15) напоминает о простой теореме из школьного курса геометрии на плоскости, касающейся свойств равносторонних треугольников: для любой точки внутри такого треугольника сумма ее расстояний (т. е. T₁, T₂, T₃) до сторон треугольника равна его высоте (т. е. Q). Это позволяет ввести на плоскости (T₁, T₂) для рассматриваемого распада треугольную систему координат, что делает симметрию диаграммы Далица явной (см. рис. 10.2). Заметим, что для бинарных реакций, анализируемых в терминах переменных Мандельстама s, t и u, тоже можно использовать треугольную систему координат, так как эти переменные удовлетворяют соотношению (3.3), аналогичному (10.15).

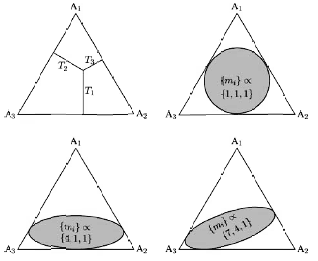
Рис. 10.2. Определение треугольной системы координат для диаграммы Далица в терминах кинетических энергий (вверху слева) и границы диаграммы Далица в нерелятивистском случае: (а) для распада на три тождественные частицы (справа вверху), (Ь) для распада на три частицы, массы которых соотносятся как 4:1:1 (слева внизу) или (с) 7:4:1 (справа внизу). Такие соотношения масс соответствуют, например, распадам η → 3π, η' → ηππ и аннигиляции p ¯ p —> η'ηπ соответственно [70].

    В каждой точке внутри треугольника выполняется закон сохранения энергии. Для нахождения границ физической области удобно ввести новые координаты. Именно:

1. начало системы координат поместим в центр треугольника (точка T₁ = T₂ = T₃ = Q/3);
2. будем отсчитывать от него полярные координаты (r, φ).

Можно убедиться, что:

Подставив новые координаты в уравнение (10.8) для границы диаграммы Далица получим:

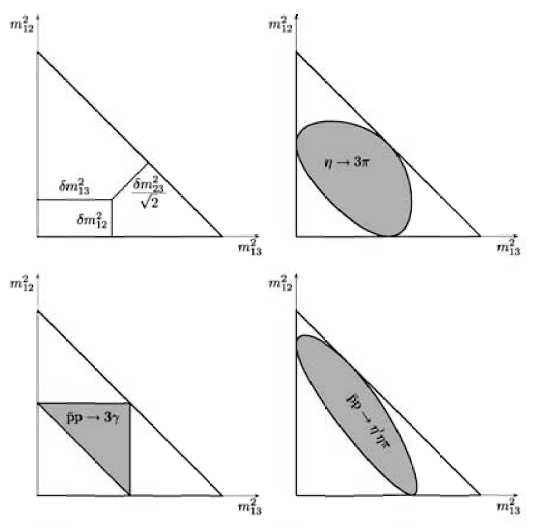
Рис. 10.3. Диаграммы Далица в релятивистском случае. Показаны те же диаграммы, что и на предыдущем рисунке, но в других терминах. Обозначение 5mij означает превышение квадрата эффективной массы m ij системы частиц (i + j) над ее минимально допустимым значением (m_i + m_j)². Распад: η → 3π, реакции: p → 3γ, p → η' ηγ (работа [70]).

    Величина ε − относительное энерговыделение − полностью характеризует кривую, задающую границу диаграммы Далица.
    В случае неравных масс тоже можно представлять диаграмму Далица в треугольной системе координат, но степень ее симметрии будет иной (см. рис. 10.2, нижние диаграммы).
    Представление диаграмм Далица в переменных s₁, s₂ дано на рис. 10.3 и рис. 10.4 (квадрат эффективной массы системы (1 + 2) есть не что иное, как s₁, а для (2 + 3) системы то же верно по отношению к s₂).

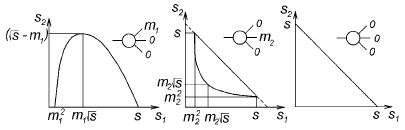
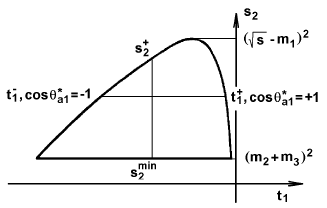
Рис. 10.4. Диаграммы Далица для особых комбинаций масс частиц-продуктов распада, когда массы двух из трех частиц или всех трех частиц равны нулю [3].

10.1.4 Конфигурации импульсов на диаграмме Далица

    Уравнение (10.8) для границы диаграммы Далица является дополнительным (по отношению к закону сохранения энергии-импульса) условием на направления и величины трехмерных импульсов частиц конечного состояния. Рассмотрим его следствия, выбрав систему покоя распадающейся частицы (т. е. центр масс продуктов распада).
    Довольно очевидно, что на границе диаграммы Далица векторы импульсов p₁, p₂, p₃ коллинеарны, однако различны их величины и направления: векторы некоторых импульсов могут быть параллельны или антипараллельны. Рис. 10.5 помогает понять, как меняются конфигурации импульсов конечных частиц при движении вдоль границы либо внутри диаграммы.
    Три характерных точки на границе диаграммы Далица отвечают минимальным значениям эффективных масс

= (₁ + ₂)² = (m₁ + m₂)²,
= (₂ + ₃)² = (m₂ + m₃)²
и = (₁ + ₃)² = (m₁ +m₃)²;

на рисунке 10.5 они обозначены как A₁, A₂, A₃. Условие минимальности квадрата эффективной массы означает, что скорости частиц рассматриваемой пары равны, их направления совпадают, а величины импульсов относятся как p₁/p₂ = m₁/m₂.
    Другие три характерные точки на этой границе отвечают максимальным значениям инвариантов = (√s − m₃)²) и т. д.; они обозначены как B₁, B₂, B₃ на том же рисунке. В этих точках направления импульсов соответствующих частиц пары противоположны, а третья частица имеет нулевую кинетическую энергию.

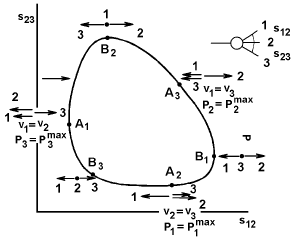
Рис. 10.5. Конфигурации векторов импульсов частиц-продуктов распада на границах диаграммы Далица (импульсы рассматриваются в общей системе центра масс). Точки B₁, B₂, B₃ отвечают максимальным значениям квадратов эффективных масс , , : точки A₁, A₂, A₃ − минимальным значениям этих величин [3].

10.2 Диаграммы Далица и симметрии: примеры

    Уже не раз говорилось о том, что если бы матричный элемент реакции не зависел от кинематических переменных, то распределение событий на диаграмме Далица (или, обобщенно, в фазовом пространстве для частиц конечного состояния) было бы постоянным (см. формулу (10.13)). Отклонения от равномерного распределения в фазовом пространстве связаны с динамикой реакции, а также с действием законов сохранения (дискретными симметриями). Примером может служить работа принципа Паули, если в конечном состоянии есть пара тождественных частиц-фермионов. Некоторые следствия дискретных симметрии в применении к диаграммам Далица в деталях будут рассмотрены в Части VII, на примере распределения плотности событий на диаграмме Далица при распаде мезонов разного спина и четности на три пиона.
    В этом разделе иллюстрируется использование диаграмм Далица в анализе экспериментальных данных на примере аннигиляции остановившихся антипротонов с протонами.

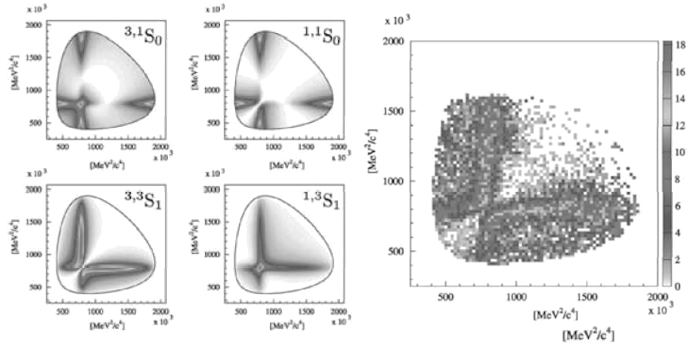
Рис. 10.6. Диаграммы Далица для аннигиляции антипротонов в пару каонов и пион: p → K^±K_s . Мишень: жидкий водород. Справа: реальные данные из эксперимента Crystal Barrel. Слева: результаты моделирования распределений на диаграмме Далица при разных возможных S-волновых компонентах (указаны в правом верхнем углу каждой диаграммы) волновой функции протония (атомо-подобной связанной системы p). Видно, что аннигиляция в (K^±K_s) идет из ^3,3S₁ состояния (работа [70]).

    Сравнение с экспериментальными данными ожидаемого вида распределения событий на диаграмме Далица при учете законов сохранения четности, изоспина и углового момента позволяет, как видно из рисунка 10.6, сделать выводы о квантовых числах (p) системы, аннигилирующей в три мезона.
    Информативная мощь и наглядность диаграммы Далица по сравнению с распределениями, проинтегрированными по одной из независимых кинематических переменных, видна из сравнения рисунков 10.7 и 10.8.

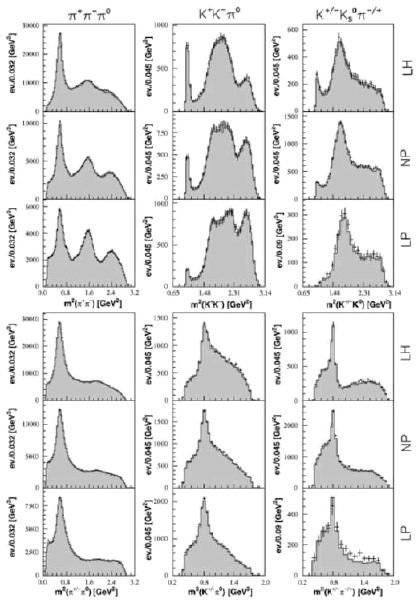
Рис. 10.7. Распределения по эффективным массам (т. е. проекции соответствующих диаграмм Далица) для аннигиляции антипротонов в мезоны при различных плотностях водородной мишени. Слева: аннигиляция остановившихся антипротонов в π⁺π⁻π⁰ систему. В центре: p → K⁺K⁻π⁰; справа: p → K^±K_s. LH − жидководородная мишень, NP - газовая водородная мишень при нормальном давлении, LP − газовая водородная мишень при низком давлении (работа [70]).

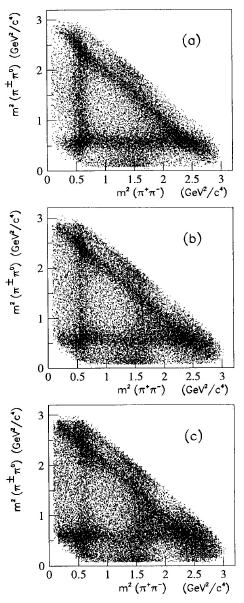
Рис. 10.8. Диаграммы Далица для реакции p → π⁺π⁻π⁰ с остановимшимися антипротонами при разных плотностях водородной мишени: (а) жидкий водород; (b) газообразный водород при нормальных давлении и температуре; (с) водород при пониженном давлении. Фон вычтен, поправки на аксептанс установки не введены. Одно событие изображается двумя точками, каждая − с весом 1/2 (работа [68]).

    Рис. 10.8 следует сравнивать с рис. 10.7; видно, что диаграмма Далица несравненно яснее. Например, она позволяет легко увидеть, что с изменением плотности мишени меняются квантовые числа (p) системы, составляющие ансамбль ее начальных состояний при аннигиляции антипротона с протоном в три мезона.

10.3 Диаграмма Чу и Лоу

    Здесь уместна цитата из книги [2] (стр. 332): "Когда частицы возникают в результате распада, чертят диаграмму Далица. Когда они возникают при соударении двух частиц, прибегают к диаграммам Чу-Лоу или Ван-Хова"¹.

Рис. 10.9. Кинематическая диаграмма для реакции 2 → 3. Обозначения очевидны; иллюстрируется определение переменных t₁ и t₂ (квадраты переданных 4-импульсов).

    В реакциях типа a + b → 1 + 2 + 3 начальное состояние имеет в системе центра масс выделенное направление, заданное импульсом падающего пучка p_a = -p_b. Общее число переменных, характеризующих конечное состояние, равно 5; в случае бесспиновых частиц таких переменных 4 (см. рис. 10.9). Поэтому при построении диаграмм типа тех, что рассмотрены выше, приходится интегрировать по остальным переменным либо во всем фазовом объеме, либо в каких-то интервалах.
    Оставим в стороне все, что связано со спином (в том числе − переменные, характеризующие ориентации спинов). Рассмотрим основные инварианты, определение которых поясняется диаграммой 10.9.

s ≡ sab = ( a + b)2 = (1 + 2 + P3)2, s1 ≡ s12 = (1 + 2)2 = (a + b − 3)2, s2 ≡ s23 = (2 +3)2 = (a + b − 1)2, t1 ≡ ta1 = (a − 1)2 = (2 + 3 − b)2, t2 ≡ tb3 = (b − 3)2 = (1 + 2 − a)2.

(10.18)

    В дополнение к этим инвариантам, можно определить еще пять, связав между собой не соседние частицы; эти инварианты можно выразить через массы частиц и инварианты из (10.18). Обозначения для них удобно давать по тому же принципу, что и в (10.18); это инварианты t_a2, t_b2, t_a3, t_b1, s₁₃ (см. [3]).
    Наконец, все скалярные произведения типа ( i · j), i,j = a, b,1, 2, 3 можно тоже выразить через массы частиц и основные инварианты из (10.18).
    Обычно, процессы с числом частиц в конечном состоянии более двух кинематически анализируются методом факторизации фазового объема, то есть последовательным разбиением процесса 2 → n на подпроцессы (2 → (n − 1), (1 → 2)) и т. д. (такая процедура подробно разобрана в книге Г.И. Копылова [2]). Для реакций типа 2 → 3 это означает разбиение на 2 → 2 и 1 → 2.
    Для определенности рассмотрим такое разбиение процесса (10.9): a + b → 1 + X, X → 2 + 3, где система X имеет эффективную массу √s₂. В этом случае для 1-го подпроцесса основными кинематическими переменными становятся t₁ (квадрат переданного при рождении системы X четырехимпульса) и квадрат эффективной массы этой системы s₂.
    На плоскости (t₁, s₂) область, где реакция кинематически разрешена, будет (как и в случае диаграммы Далица) ограничена некоторой замкнутой кривой. Представление распределений физических событий на этой плоскости, напоминающее распределения на диаграмме Далица, называют диаграммой Чу-Лоу.

Рис. 10.10. Диаграмма Чу-Лоу; пример дан для случая, когда t₁ = (m_a − m₁)² лежит вне физической области [3].

10.3.1 Границы и фазовая плотность

    Найти уравнение границы физической области для диаграммы Чу-Лоу можно примерно так лее, как это было проделано для диаграммы Далица.
    Стартуем с выражения для трехчастичного фазового объема:

(10.19)

    Используем тождество:

(10.20)

где . Вставив это тождество в (10.19), получим:

(10.21)

что означает

R3(s) = ∫ds2R2 (s; , s2) R2 (s2;, ).

(10.22)

Можно убедиться, что (10.22) легко записать в форме

(10.23)

Рис. 10.11. Диаграмма Чу-Лоу; пример дан для случая, когда t₁ = (m_a − m_i) лежит в физической области; m_b = m₂ = m₁ = 1 (т. е. все величины измеряются в единицах массы мишени m_b); m₅ = 5,
m₃ = 2, s = 60 (из книги [3]).

    Физическую область для реакции m_a + m_b → m₁ + √s₂ можно найти так:

• выпишем выражения для s2 и t1 в с.ц.м.:
• потребуем выполнения условия

Этими условиями определяются границы области интегрирования в (10.23). Опустив подробности (их молено найти в [3]), выпишем конечный результат для границы физической области в процессе
2 → 3:

(10.25)

    Важно отметить, что когда точка с фиксированным значением s₂, изображающая конечное событие или группу событий с данными кинематическими параметрами, движется поперек диаграммы Чу-Лоу, величина t₁ линейно меняется с изменением косинуса θ_a1^*.
    Важное свойство диаграммы Чу-Лоу состоит в том, что фазовая плотность на ней не зависит от t₁, но зависит от s₂ и равна

(10.26)

    Осталось отметить, что на диаграмме Чу-Лоу физическая область на плоскости (t₁, s₂) размещена так, что одновременно выполняются два условия:

λ(s,s2,) ≥ 0 , λ(s2,,) ≥0,

(10.27)

10.3.2 Фазовая плотность и отношение потоков

    Сравнивая формулу (10.26) с формулой (10.13) для фазовой плотности в диаграмме Далица, можно заметить определенное сходство между ними: первый множитель в (10.26) соответствует правой части формулы (10.13), где s заменяется на s₂ (как будто бы реакция a + b → 1 + 2 + 3 была обращена во времени в реакцию 2 + 3 → 1 + a + b: при таком обращении s₁ переходит в t₁). Второй множитель в формуле (10.26) выглядит как отношение инвариантных (Мёллеровских) потоков во входном канале a + b и парциальном выходном канале 2 + 3, то есть, имеет смысл той доли потока частиц во входном канале, которая досталась возникшей в реакции системе 2 + 3. Похожее отношение уже встречалось в Части III при обсуждении реакции фрагментации дейтрона "вперед" как модели фрагментации адронов в партонной картине (формула (4.9)). Оказывается, что это сходство не столь уж и случайно.
    Действительно, вернемся к левой диаграмме рис. 4.3. Соответствующий ей матричный элемент включает множители, соответствующие верхней вершине, пропагатору нейтрона и нижней вершине. В квадрате модуля этого матричного элемента связанный с верхней вершиной фактор дается формулой (4.7); пропагатор нейтрона дает фактор (1 − α)^-1 при рассмотрении задачи в динамике на световом фронте (точнее, в пределе бесконечного импульса дейтрона-снаряда). Остается рассмотреть фактор, связанный со взаимодействием нейтрона с мишенью (нижняя вершина). При отсутствии теории, позволяющей вычислить этот фактор "из первых принципов". можно попытаться вычленить хотя бы его зависимость от кинематических переменных, отказавшись от строгого вычисления абсолютной величины сечения в стандарных единицах (миллибарнах).
    Обратим внимание на то, что если рассматривать только вершину взаимодействия нейтрона с мишенью (n + Target), или, сокращенно, (nT), то при инклюзивной постановке эксперимента (когда по всем возможным конечным состояниям после такого взаимодействия производится суммирование и интегрирование по всему разрешенному фазовому пространству), ее можно было бы связать с полным сечением (nT) рассеяния по формуле (9.11) с учетом формулы (9.6), записав ее в обобщенном виде как

(10.28)

    В этой формуле числитель как раз и соответствует фактору, связанному с обсуждаемой вершиной. Если бы в ней мы имели бы дело со свободным реальным нейтроном, то это сечение можно было бы взять непосредственно из известных экспериментальных данных. При этом инвариантный поток InvFlux(nT) следовало бы также брать для системы (свободный реальный нейтрон + мишень).
    Но в рассматриваемом случае нейтрон передается от дейтрона-снаряда. Вообще говоря, он даже не находится на массовой поверхности. (Правда, при использовании техники светового фронта и, в частности, предела бесконечного импульса, его можно считать находящимся на массовой поверхности, что и предполагается далее.) Поэтому, во-первых, вклад (nT) вершины не полностью соответствует полному сечению (nT) рассеяния: из него следует исключить вклад упругого рассеяния (по крайней мере часть). Во-вторых, эта вершина не обязательно в точности такая же, как для рассеяния свободного реального нейтрона. Впрочем, если последним различием пренебречь, то с учетом всего уже сказанного, можно воспользоваться формулой (10.28), но взять инвариантный поток для системы (передаваемый нейтрон + мишень):

(10.29)

Теперь известны все факторы, определяющие сечение фрагментации дейтрона согласно диаграмме рис. 4.3 в описанной картине, и для получения формулы (4.8) остается снова воспользоваться (10.28), взяв инвариантный поток для системы (дейтрон+мишенъ). то есть InvFlux(dT). В полученной после этого формуле появится отношение

(10.30)

    Из приведенного примера и сравнения полюсной диаграммы для реакции фрагментации дейтрона с общей кинематической диаграммой рис. 10.9 или т. н. "деревом импульсов" рис. 10.12 наглядно видны происхождение и смысл второго множителя в формуле (10.26): часть начального потока частиц a и b уносится частицей 1, а остальная приходится на долю "промежуточной" системы, превращающейся затем в частицы 2 и 3. Величину этой доли определяет второй множитель в формуле (10.26).

Рис. 10.12. Диаграмма "дерева импульсов": кинематической редукции реакции рождения нескольких частиц к последовательности реакций типа двухчастичного распада. Частицы начального состояния a и b "объединяются" в промежуточное состояние X_аb с массой √s, которое затем распадается на частицу 1 и псевдочастицу X₂ с массой √s₂, в свою очередь распадающуюся на конечные частицы 2 и 3. Каждому из последовательных двухчастичных распадов доступен двухчастичный фазовый объем R₂. Соответственно, посредством подобной редукции полный фазовый объем многочастичной реакции a + b → 1 + 2 + 3 + ... может быть выражен через интегралы от соответствующих двухчастичных фазовых объемов.

(1) Повидимому, стоит уточнить это высказывание в том, что к диаграммам Чу-Лоу или Ван-Хова сегодня обращаются только при анализе процессов с невысокими множественностями конечных состояний.