Глава 11 Диаграммы Далица и дискретные симметрии

11.1 Симметрии и распределение событий на диаграмме Далица

    До сих пор в обсуждениях фазового объема, диаграмм Далица и Чу-Лоу матричный элемент реакции считался константой. Обсуждение было сосредоточено на чисто кинематических факторах, влияющих на величину сечений и на форму распределений по кинематическим переменным. Пришло время вернуться к матричному элементу, который определяется не только динамикой рассматриваемого процесса, но и законами сохранения существенных для него квантовых чисел. Рассмотрим, как проявляются эти законы в структуре матричного элемента и в форме распределений событий в диаграмме Далица на примере распада нейтрального изоскалярного мезона АЛ в три пиона: → π⁺π⁻π⁰. Матричный элемент распада обозначим как < 3π | T | > = _α(p_i, E_i), где индекс α помечает спиновые состояния распадающегося мезона и принимает только одно значение 1, если спин мезона равен нулю (тогда про этот индекс можно  забыть), три значения (-1,0,1) − если спин мезона равен 1 и т. д. Заметим, что для рассматриваемого случая диаграмма Далица в треугольных координатах (E₁, E₂, E₃) симметрична и вписана в равносторонний треугольник с высотой, определяемой энерговыделением при распаде (см. раздел 10.1.3).
    Поскольку четность считается сохраняющейся, так как распад идет за счет сильного взаимодействия, и поскольку пионы - псевдоскалярные частицы, то матричный элемент должен удовлетворять условию

α(-pi, Ei) = (-1)α(pi, Ei),

(11.1)

где − внутренняя четность распадающегося мезона.
    Итак, изоспин начального состояния равен нулю: I_in =. Изоспин конечного состояния тоже должен быть равен нулю. Можно показать (пользуясь законами сложения угловых моментов, поскольку для изоспина они такие же, как и для углового момента), что трехпионное состояние с нулевым полным изоспином может быть представлено через пионные состояния так (cм. главу 15, раздел 15.2.):

Видно, что конечное трехпионное состояние с нулевым полным изоспином антисимметрично при перестановке любых двух пионов. Эти два условия, (11.1) и (11.2), приводят к весьма важным следствиям для матричного элемента и, соответственно, для распределения событий на диаграмме Далица.
    Действительно, полный матричный элемент < 3π | T | > должен быть скаляром. В него входит, очевидно, волновая функция распадающегося мезона (скаляр, если это скалярный мезон, псевдоскаляр - если это псевдоскалярный мезон, вектор - если этот мезон векторный и т. д.) и величины, характеризующие трехпионное конечное состояние; это энергии мезонов и/или их импульсы, скомбинированные так, чтобы после умножения _α(p_i, E_i) на волновую функцию мезона получилась скалярная величина.

11.1.1 Распад мезона со спином 0 на три пиона

В этом случае матричный элемент _α(p_i, E_i) должен быть скалярной функцией энергий мезонов конечного состояния, причем такой. чтобы выполнялось условие антисимметричности при перестановках любой пары пионов, следующее из (11.2). Уже поэтому ясно, что эта скалярная функция не может быть константой и должна зависеть от энергий мезонов. Ясно также, что матричный элемент должен зануляться при E₁ = E₂, или E₃ = E₂, или E₁ = E₃, то есть, на диаграмме Далица плотность событий должна зануляться вдоль линий, отвечающих этим условиям.
    Наиболее общей функцией, удовлетворяющей всем описанным здесь условиям, является

α(pi, Ei) = (E1 − E2)(E2 − E3)(E3 − E1) − ƒ(E1,E2,E3),

(11.3)

где функция  ƒ(E₁,E₂,E₃) симметрична при перестановке любых двух ее аргументов. При равенстве любых двух ее аргументов она должна оставаться конечной (во всяком случае, если она и расходится, то медленнее, чем стремится к нулю разность этих же аргументов). Предположим, что эта функция меняется так слабо при движении по диаграмме Далица точки, соответствующей конкретной конфигурации энергий частиц конечного состояния, что ее можно считать практически постоянной. Тогда вся зависимость матричного элемента от кинематических параметров будет определяться первым множителем в (11.3).
    Если теперь перейти от энергий к полярным координатам r и φ (см. параграф 10.1.3), то плотность вероятности на диаграмме Далица окажется такой:

    Отсюда видно, что плотность событий максимальна вблизи границы диаграммы Далица, причем абсолютные максимумы плотности находятся в точках nπ/6, n = 1, 3, ...,11 (6 точек). На линиях nπ/6,
n = 0, 2, ..., 10 плотность точек равна нулю (см. рис. 11.1).

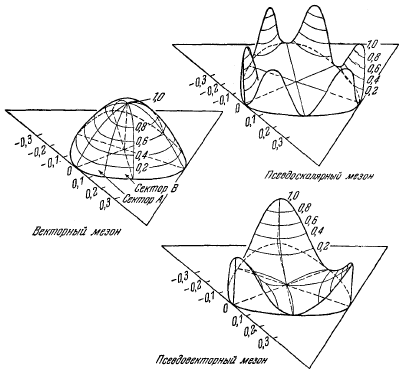
Рис. 11.1. Диаграммы Далица для распада на три пиона 0⁻, 1₊ и 1⁻ мезонов [8].
 Трехмерные картины распределений плотности вероятности.

    Заметим, что вид (11.3) означает, что матричный элемент инвариантен при отражениях, и т. о. четность нашего мезона должна быть отрицательной в силу (11.1).
    Можно было бы предположить, что истинно скалярный мезон все же может распасться на 3 пиона. Но в этом случае, с учетом псевдоскалярности пионов и того факта, что полный момент конечного состояния должен быть нулевым (ибо в начальном состоянии от равен нулю по предположению), матричный элемент надо было бы построить из псевдоскалярной комбинации трех импульсов. Такая комбинация существует; например, это детерминант из компонент всех трех импульсов. Но сумма всех импульсов в системе центра масс равна нулю и этот детерминант тождественно обращается в нуль! Это означает, что из-за сохранения четности скалярная частица (с четностью +1) не может распасться на три пиона.

11.1.2 Распад векторного мезона на три пиона

    В этом случае полный угловой момент в начальном состоянии равен 1, а четность начального состояния равна -1.
    В силу (11.1) и векторного характера волновой функции мезона , матричный элемент должен быть псевдовектором. Такой псевдовектор, антисимметричный при перестановках пары пионов, может быть построен; комбинация

удовлетворяет всем поставленным условиям; функция ƒ − скалярна и симметрична при перестановках аргументов. Второе соотношение в (11.5) позволяет переписать первое в виде

Плотность событий на диаграмме Далица будет определяться квадратом этого матричного элемента, и опять, если функция ƒ практически константа в разрешенной кинематикой области диаграммы Далица, то можно показать, что

dρc.m./dS = const ·

(11.7)

что в полярных координатах сводится к выражению

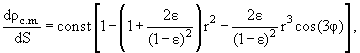(11.8)

где величина ε определена в (10.17).
    Можно отметить следующее: (1) функция в квадратных скобках как раз та, что определяет границу диаграммы Далица в случае распада на три частицы одинаковой массы; условие границы есть равенство нулю этой функции (см. предыдущие лекции). То есть, на границе диаграммы Далица плотность вероятности обращается в нуль для рассматриваемого случая. (2) Максимум плотности вероятности достигается в центре диаграммы Далица. (3) На границе диаграммы Далица импульсы частиц либо равны нулю, либо коллинеарны − откуда тоже (без обращения к (11.8)) следует, что плотность вероятности обращается в нуль на границе диаграммы Далица. На рис. 11.1 все это наглядно видно.

11.1.3 Распад псевдовекторного мезона на три пиона

    В этом случае полный момент в начальном состоянии равен 1, а четность начального состояния +1.
    В силу (11.1) и псевдовекторного характера волновой функции мезона , матричный элемент должен быть вектором. Рассуждая примерно так же, как в предыдущих случаях, можно прийти к выводу о том, что матричный элемент, антисимметричный по перестановкам пары мезонов, должен иметь вид

    Приняв во внимание законы сохранения энергии и импульса, это выражение можно привести к виду

откуда видно сразу, что в центре диаграммы Далица плотность вероятности обращается в нуль (так как в этой точке E₁ = E₂ = E₃ = M/3). Кроме того, из (11.9) видно, что на границе диаграммы Далица в точках, где p₁ = p₂, или p₂ = p₃, или p₁ = p₃ плотность вероятности также обращается в нуль (т. к. зануляется матричный элемент). Зато в тех точках, где p₁ = -p₂, или p₂ = -p₃, или p₁ = -p₃, плотность вероятности максимальна (см. рис. 10.5 и рис. 11.1).
    Если перейти к полярным координатам, как и в двух предыдущих случаях, то можно получить:

(11.11)

11.2 Классификация диаграмм Далица

    Фактически, в предыдущем разделе были рассмотрены особые точки и линии на диаграмме Далица для трехпионного распада изоскалярного мезона, связанные с квантовыми числами начального и конечного состояний. Все отклонения от изотропного распределения событий на диаграмме Далица, связанные именно с динамикой реакции, остались спрятаны в скалярной функции ƒ. Например, в ней "спрятаны" резонансы, которые могли бы быть в системе двух пионов.

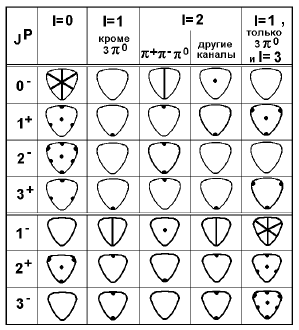
Рис. 11.2. Классификация диаграмм Далица для распада на три пиона различных мезонов [2].

    Классификацию особых точек и линий на диаграмме Далица для трехпионных распадов мезонов с различными квантовыми числами можно найти, например, в книге [2] (рис. 11.2). Запрещенные для событий области показаны жирными линиями или точками; там, где они пересекаются, возникают более сильные запреты.
    Подобные схемы часто применяют для определения квантовых чисел резонансов (в рассмотренных здесь случаях в роли такого резонанса выступал мезон ), поскольку каждой отдельной комбинации квантовых чисел изоспина I, спина J и четности P, т. е. набору (I J^P), отвечает своя, достаточно характерная, конфигурация запрещенных областей на диаграмме Далица.
    При обсуждении диаграмм Далица в Части VI, отмечалось одно из ее важнейших свойств: постоянство фазовой плотности (распределения событий), если квадрат матричного элемента реакции не зависит от положения события внутри разрешенного кинематикой (в узком смысле) фазового объема. Только что рассмотренные примеры показывают, во-первых, что это уже не так, если кинематика понимается в широком смысле, и во-вторых, что законы сохранения дискретных квантовых чисел позволяют определить общий характер зависимости квадрата матричного элемента реакции от кинематических переменных. Конкретный характер такой зависимости определяется уже динамическими механизмами реакции.