|
|
|
(15.1) |
в котором 3×3 матрица R с элементами Rij, очевидно, зависит от r. Если записать компоненты Ai в виде вектор-столбца, то в матричных обозначениях соотношение (15.1) будет выглядеть как
| Ar = R · A. | (15.2) |
Например, если r = rу(θ) (вращение на угол θ вокруг оси Y), то
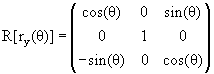 |
(15.3) |
Как правило, обычно используется набор трех ортогональных единичных базисных
векторов e(i), направленных вдоль трех координатных осей. Если
поворачивается один из них, скажем, e(i), то компоненты
вектора
![]() будут связаны с компонентами e(i) в соответствии с (15.1). Но
можно представить
будут связаны с компонентами e(i) в соответствии с (15.1). Но
можно представить
![]() в
виде линейной комбинации e(i) и увидеть, что
в
виде линейной комбинации e(i) и увидеть, что
|
|
(15.4) |
где RT есть транспонированная матрица R. (Напомним, что матрица
вращений R ортогональная: RTR = RRT =
1.)
Подчеркнем, что в (15.1) для
преобразования координат фигурирует R, а для преобразования ортов (в формуле
(15.4)) − транспонированная матрица этого вращения.
Обсудим вопрос о том, как связаны
между собой описания одного и того же физического объекта, которые дают разные
наблюдатели, использующие разные координатные системы (здесь речь идет пока
только о вращениях, т. е. используемые системы координат различаются только тем,
что они повернуты относительно друг друга).
Пусть A есть
фиксированный вектор, компоненты которого в системе S наблюдателя O есть Aj.
To есть.
| A = ∑j Aj · e(j). | (15.5) |
Пусть O' - наблюдатель, использующий систему отсчета Sr,
повернутую относительно S вращением r. Естественно, что он использует свои
базисные вектора
![]() и
для него
и
для него
|
A = ∑l (Al)Sr
·
|
(15.6) |
То есть, с учетом (15.4),
| (Ai)Sr = Rij (r-1) · Aj, | (15.7) |
где использовано соотношение
| [R(r)]-1 = R(r-1). | (15.8) |
Иными словами, если система
отсчета поворачивается вращением r, то компоненты фиксированного вектора,
наблюдаемого в системах Sr и S, связаны через R(r-1), в
отличие от (15.1).
Для спиноров спина s рассмотрение
проводится в полной аналогии с проведенным выше для обычных трехмерных векторов.
Именно, вводятся (2s + 1) базисных спинора η(m) следующего вида:
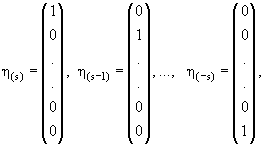 |
(15.9) |
которые представляют собственные состояния оператора s и спинор общего вида записывается в виде
| χ = ∑m χm · η(m) | (15.10) |
Числа χm имеют смысл "компонент" спинора χ. По аналогии с (15.7), компоненты этого спинора в повернутой системе отсчета (χm)Sr связаны с его компонентами χm следующим образом:
|
|
(15.11) |
где матрицы ![]() s(r-1)
являются матрицами (2s+1)-мерного представления группы вращений r. (Они, как
известно, унитарны:
s(r-1)
являются матрицами (2s+1)-мерного представления группы вращений r. (Они, как
известно, унитарны:
![]() †
†![]() =1.) По аналогии с (15.4), для базисных спиноров ("ортов"):
=1.) По аналогии с (15.4), для базисных спиноров ("ортов"):
|
|
(15.12) |
Это уравнение можно истолковать так: состояние, описываемое наблюдателем O в
системе S как η ( m ), описывается наблюдателем Or . работающим в
повернутой относительно S системе координат, суперпозицией состояний ηr(m'),
выбранных им в качестве базисных.
Иными словами: когда наблюдатель O в системе отсчета S видит
частицу спина s в состоянии
| sm >, наблюдатель Or, чьей системой отсчета
является Sr, полученная из S вращением r, видит состояние частицы как
| sm >Sr, где
|
|
(15.13) |
Опять, по аналогии с рассмотренным ранее случаем трехмерного обычного вектора, можно говорить об активном преобразовании (вращении) состояния | sm > в | sm >r, и сравнивая с (15.4), понимать | sm >r как вектор состояния, заданный
|
|
(15.14) |
что можно записать немного в другом виде, как это принято в квантовой механике, а именно, ввести оператор U(r), представляющий вращение r и действующий прямо на вектор состояния:
| | sm >r = U(r)| sm >. | (15.15) |
Отсюда видно, что
|
|
(15.16) |
и выражение (15.13) приобретает вид
| | sm >Sr = U(r-1)| sm >. | (15.17) |
Несколько примечаний о специфике случая спина 1/2.
- Матрицы Паули σj с одной стороны, представляют компоненты оператора спина ŝj, а с другой - образуют базис для разложения 2×2 эрмитовых матриц. Для случая более высокого спина s наиболее общая эрмитова матрица характеризуется (2s + 1)2 вещественными параметрами, и набор трех матриц Si, аналогичных матрицам Паули, никак не может дать базис для такого разложения.
- Двухкомпонентный спинор χ наиболее общего вида может быть охарактеризован четырьмя вещественными параметрами, из которых один, представляющий общую фазу, несуществен. Если этот спинор нормирован на единицу, то остаются два независимых вещественных параметра. То есть, без потери общности можно записать
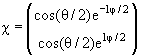 |
(15.8) |
Если теперь вычислить вектор поляризации
χ, определенный как
|
|
(15.19) |
то окажется, что
|
|
(15.20) |
Вектор
χ принято называть вектором поляризации для состояний χ. Его знание полностью характеризует эти состояния.
- В случае более высоких спинов поляризационный вектор для состояния χ определяется как
|
|
(15.21) |
но теперь недостаточно знать три компоненты
χ, чтобы зафиксировать [2(2s + 1) − 2] независимых параметра (2s +1)-мерного спинора χ.
Наконец, матрицы Si, представляющие спиновые операторы ŝi для спина s преобразуются при вращениях как вектор, то есть
|
|
(15.22) |
- Для спина 1/2 соотношение (15.22) хорошо известно в своей эквивалентной, но несколько более простой форме, связывающей ожидаемые (средние) значения в системе Sr с соответствующими средними в S:
| (σi)Sr = Rij (r-1) <σj>. | (15.23) |
Спин и спиральностъ в релятивистском случае.
В релятивистской теории частице сопоставляется
инвариантное спиновое квантовое число s. Но только в случае, когда частица
покоится, можно указать соответствующий набор спиновых операторов s и далее
действовать так, чтобы использовать обычный формализм нерелятивистской квантовой
механики. Можно показать, что действие вектора Паули-Любанского на состояния в
системе покоя как раз те же самые, что и у операторов углового момента
![]() i,
так что все свойства нерелятивистского спина относительно вращений сохраняются и
для покоящейся частицы.
i,
так что все свойства нерелятивистского спина относительно вращений сохраняются и
для покоящейся частицы.
Поэтому для частицы в покое удобно зафиксировать систему
отсчета и далее классифицировать ее состояния в точности так же, как в
нерелятивистском случае, т. е. используя собственные состояния | ssz
> операторов ŝ2
и ŝz.
Однако, для движущейся частицы классификация состояний не так очевидна.
Стандартный подход к получению состояний произвольного
импульса состоит в том, чтобы подействовать на состояния покоя соответствующим
Лоренцевым преобразованием. Рассмотрим другой, более физичный, но эквивалентный
способ решения этой проблемы. Применим тот же способ рассуждений, что был
использован только что, при рассмотрении преобразований вращения.
Обозначим произвольное физическое преобразование Лоренца как
l и будем по-прежнему обозначать физическое вращение как r, а чистые
Лоренцевы преобразования вдоль осей координат как lj, j = x,
y, z.
Надо отметить, что последовательность преобразований важна.
Например, если сначала повернуть систему S вокруг ее оси y на угол θ (назовем
полученную систему S'), а затем сделать чисто Лоренцево преобразование в
новую систему S", двигающуюся со скоростью v вдоль оси Z системы S',
то полное преобразование из S в S" можно представить как
| S → S" = lz' (v) ry (θ) S. | (15.24) |
Чисто Лоренцево преобразование в произвольном направлении обозначается как l(v), где, по соглашению,
| l(v) ≡ [r-1(v)]"lz' (v) r(v). | (15.25) |
Здесь r (v) есть вращение вокруг e(z)×v
такое, что оно поворачивает ось Z на направление v, a [r-1(v)]
есть обратное к нему, но приложенное к "убыстренной" системе.
Если на 4-вектор A подействовать физическим Лоренцевым
преобразованием l, то оно преобразует этот вектор в новый вектор A1.
Компоненты A1 связаны с компонентами вектора A согласно
|
|
(15.26) |
где 4×4 матрица Λ зависит от l. Когда это просто вращение, имеем:
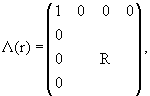 |
(15.27) |
где R − матрица, определенная в (15.1). Если же l есть чистое Лоренцево преобразование ("буст") к скорости v вдоль оси z, то
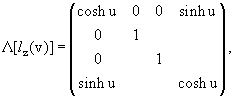 |
(15.28) |
где cosh u = (1 − v2)-1/2 или tanh
u = v.
Теперь ограничимся случаем частиц ненулевой массы2.
Возьмем некоторую систему отсчета SA, в которой частица A массы m
покоится и находится в состоянии | s,sz >. Пусть O − наблюдатель,
движущийся со скоростью -v отн|ительно SA. Возьмем v =
p/(p2 + m2)1/2, где p есть
некоторый (произвольный) импульс. Тогда наблюдатель O, глядящий на A, которая
покоится в SA, увидит частицу, движущуюся с импульсом p.
Поэтому, описывая ее состояние, он пометит это состояние меткой p, т. е.
как | p... >. Однако очевидно, что с наблюдателем O связано бесконечно
много систем отсчета S, и все они движутся со скоростью -v относительно SA.
Если одну из этого бесконечного множества систем отсчета пометим как S1,
то все остальные могут быть получены из S1 некоторым вращением S1
как жесткого тела вокруг p. Ясно, что все наблюдатели, связанные с этими
системами, будут видеть частицу двигающейся с одним и тем же импульсом p,
но в разных спиновых состояниях, так как их системы отсчета повернуты
относительно друг друга. Т. о. "спиновые" метки, задающие состояние движения A,
должны зависеть от того. какую систему отсчета выбрал наблюдатель O. Этот выбор
является предметом некоторого соглашения. Существуют две основных конвенции, а
именно:
а) Канонический выбор.
Здесь O выбирает свою систему отсчета S так, что она получается из SA
чистым Лоренцевым преобразованием l(-v) как в (15.25). В
этом случае он помечает состояние движения, которое он видит, как | p, sz
>.
б) "Спиральный" выбор.
Пусть p имеет полярные углы (θ, φ). Тогда наблюдатель O выбирает свою систему отсчета следующим образом: для начала он делает преобразование в систему S', движущуюся со скоростью
v = | p |/(p2 + m2)1/2
в направлении, противоположном направлению оси Z системы AA.
Затем наблюдатель выполняет такое преобразование S',
чтобы получить импульс A совпадающим с p = (p, θ, φ). Простейшее вращение
для этого − сначала на угол (-θ) вокруг оси OY', затем на угол
(-φ) вокруг новой Z-ocи − OZ", то есть, полное преобразование есть
| SA → S = rz"(-φ) ry'(-θ) (lz)-1(v) SA. | (15.29) |
Заметим, что если использовать обычное обозначение r (α,β,γ) для вращений на эйлеровы углы α, β, γ, т. е.
| r (α,β,γ) = rz"(γ) ry'(β) rz(α), | (15.30) |
то
| S = r-1(φ,θ,0) (lz)-1(v)SA. | (15.31) |
Если состояние A в системе покоя SA есть |
![]() ; s, sz
= λ >, где
; s, sz
= λ >, где
![]() = (m,
000), то O, используя систему S, видит состояние |
= (m,
000), то O, используя систему S, видит состояние |
![]() ; s, sz
= λ >S, которое он обозначает как | p; λ >, т.е состояние |
p; λ > определяется как
; s, sz
= λ >S, которое он обозначает как | p; λ >, т.е состояние |
p; λ > определяется как
|
| p;λ > ≡ |
|
(15.32) |
а система S определена выше. Математическая связь между левой и правой частями (15.32) дана ниже. Далее в этом разделе, если не оговорено противоположное, будут использоваться именно спиральные состояния, так как в этом случае формализм проще. Однако при выполнении экспериментов и представлении данных используется, как правило, именно канонический базис, когда направления спинов даются так, что это именно те направления, которые получаются в системе покоя при переходе в нее из лабораторной системы чистым Лоренцевым преобразованием типа (15.25).
Физический смысл спиральных состояний
Уравнения (15.31,15.32) особенно полезны для понимания физического смысла спиральных состояний. В самом деле, пусть в системе S мы говорим о том, что частица A имеет состояние движения, отвечающее вектору состояния | p; λ >. Тогда, согласно (15.31) и (15.32), если эту частицу наблюдать из системы SA, связанной с S через (15.31):
| SA = lz' (v) r(φ,θ,0)S, | (15.33) |
то она будет видна покоящейся со спиновой компонентой sz = λ.
Будем называть такую, выделенную из всех возможных, систему отсчета для A "спиральной
системой покоя".
Преобразование (15.33) часто обозначают специальным образом,
определяя специальный оператор h(p):
| h(p) ≡ lz' (v) r(φ,θ,0). | (15.34) |
Другой способ определить h(p), чаще встречающийся в литературе, состоит в том, чтобы все требуемые преобразования относить к одной и той же, уникальной, системе отсчета. В этом случае, как можно убедиться,
| h(p) = r(φ,θ,0)lz(v). | (15.35) |
и отсутствие "штрихов" у меток осей является существенным.
По построению, оператор h(p), действуя на 4-вектор
![]() ,
переводит его в p. Теперь, в новых обозначениях,
,
переводит его в p. Теперь, в новых обозначениях,
| S = h-1(p)SA, | (15.36) |
и в полной аналогии с (15.17),
|
| p; λ > ≡ |
|
(15.37) |
где U есть оператор, соответствующий Лоренцеву преобразованию h(p).
Обычно, рассматривая спиральные состояния, вектор состояния |
p, λ > определяют посредством (15.37), однако проведенные здесь
рассуждения позволяют прояснить смысл "метки" λ .
Действие Лоренцевых преобразований на спиральные состояния
При обсуждении экспериментальных данных
зачастую необходимо рассматривать данную физическую ситуацию в
разных системах отсчета, а именно, в лабораторной системе и системе
центра масс. Поэтому надо понять, как спиральные состояния
изменяются при действии преобразований Лоренца. Это необходимо также
и для того, чтобы разобраться в слегка затуманивающей суть дела
терминологии (Томасовская прецессия, Вигнерово вращение и т. п.)
Ограничимся здесь рассмотрением частиц с ненулевой массой.
Пусть в данной системе отсчета S наблюдатель O видит частицу A
движущейся с импульсом p и спиральностью λ, т. е. он говорит
о состоянии | p, λ >.
Пусть Sl − система отсчета, полученная в результате
действия Лоренцева преобразования l на S. Поставим вопрос: как
наблюдатель Ol будет описывать движение частицы A?
По аналогии со случаем вращения (см. (15.17)), наблюдатель Ol,
будет описывать состояние как
| | p,λ >Sl = U(l -1) | p,λ >, | (15.38) |
где U(l) − оператор, совершающий преобразование Лоренца l.
Обозначим через p' вектор импульса,
приписываемый наблюдателем Ol частице A. Его компоненты p'
µ являются, очевидно, компонентами p, как их видит Ol
(см. (15.7)):
| p' µ = (pµ)Sl = Λµν {l-1)pν. | (15.39) |
Очевидно, мы должны были бы ожидать, что | p, λ >Sl = | p', λ' >, где p' дается выражением (15.39), но что есть при этом λ' ? Чтобы ответить на этот вопрос, используя определение спиральных состояний (15.37) запишем:
|
U(l-1)| p,λ > = U(l-1)
U[h(p)] |
|
(15.40) |
Умножив обе части этого уравнения на U [h(p')] U-1 [h(p')] = 1, где h(p') есть такое спиральное преобразование, которое нужно, чтобы получить состояние | p',λ >:
|
| p',λ > ≡ U[h(p')]
|
|
(15.41) |
получим, в итоге, из (15.40):
|
U(l-1)| p,λ > = U[h(p')] |
(15.42) |
где ![]() есть
есть
|
|
(15.43) |
Из выражения (15.43) видно, что последовательность
физических операций, "спрятанных" в U, есть не что иное, как вращение,
независимо от того, каким является l. Это проще всего увидеть, рассмотрев
действие операторов h-1(p') l-1
h(p) на 4-вектор
![]() = (m,
0,0, 0,).
= (m,
0,0, 0,).
Действительно:
a) h(p) :
![]() → p
→ p
b) l-1 : p → p'
c) h-1(p') : p' →
![]()
То есть, последовательность (а),(b),(с) дает
![]() →
→
![]() и из
вида
и из
вида ![]() ясно, что только вращение может иметь такое свойство. Поэтому
ясно, что только вращение может иметь такое свойство. Поэтому
![]() представляет
вращение независимо от того, какое у нас l. Обозначим это физическое вращение
через r(l,p):
представляет
вращение независимо от того, какое у нас l. Обозначим это физическое вращение
через r(l,p):
| r(l,p) = h-1(p') l-1 h(p). | (15.44) |
Его называют "Вигнеровым поворотом спиральности" для преобразования l
осей, приводящего p к p' (это не то же самое, что
называется " Вигнеровым поворотом", разъясняемым низже).
Из (15.14) и (15.15) известно, как вращение преобразует
состояния для покоящейся частицы. Поэтому
|
|
(15.45) |
и поскольку ![]() λ'λ
есть числа, подставляя это в (15.42), (15.38) и (15.41) прихоим к соотношению
λ'λ
есть числа, подставляя это в (15.42), (15.38) и (15.41) прихоим к соотношению
|
|
(15.46) |
`Это и есть то соотношение, которое требовалось для связи между описанием состояния движения частицы в системах Sl и S. В этом виде оно справедливо для любого Лоренцева преобразования из S в Sl. Причина того, что | p, λ >Sl и | p', λ' > связаны вращением состоит в том, что спиральная система покоя частицы, достигаемая из S не та, которая достигается из Sl!
Специальные случаи "Вигнерова поворота спиральности"
Чистое вращение осей. С точки зрения
эксперимента случай, когда l есть простое вращение
относительно оси Y, один из особо важных. Можно показать, что в этом
случае r(l,p) ≡ 1, то есть никакого "Вигнерова
поворота спиральности" нет. Таким образом, если l = ry(β),
p = (p, θ, 0) и
p' = (p, θ-β, 0), то
| | p,λ > → | p',λ >. | (15.47) |
В частном случае, когда p направлен по оси вращения, надо пользоваться вместо (15.47) выражением
|
| p,λ > → exp [-iα |
(15.48) |
Преобразование из системы центра масс в лабораторную систему
Этот случай на практике является наиболее
важным. Примем обозначения: A + B → ... + K + ... и назовем "лабораторной"
системой (л.с.) ту, в которой B покоится. Будем считать также, что
направления осей в л.с. и системе центра масс (с.ц.м.) параллельны
друг другу.
Рассмотрим, для простоты, частицу массы m, рожденную в с.ц.м.
при азимутальном угле φ = 0, т. е. в плоскости XZ, так что ее
импульс и энергия в с.ц.м. и л.с. есть, соответственно,
| p = (p,θ,0), E ; pL = (pL,θL,0), EL . | (15.49) |
Из (15.35) тогда имеем:
| h(p) = ry(θ) lz(v); h(pL) = ry(θL) lz(vL), | (15.50) |
где v и vL есть скорости частицы в с.ц.м. и л.с. соответственно.
Ось Z всегда выбирается вдоль направления начального пучка −
как в с.ц.м., так и в л.с. Поэтому преобразование из с.ц.м. системы отсчета S в
л.с. систему SL соответствует "бусту" S вдоль отрицательного
направления оси Z со скоростью βCM, где βCM есть скорость
с.ц.м. системы как она видна из л.с. Иными словами, следует действовать на S
оператором lz-1(βCM), чтобы получить SL.
При таком частном выборе l в (15.44), т. е. l =
lz-1(βCM), имеем p' ≡ pL
и потому вращение
r(l,p) = r [lz-1(βCM),p]
можно характеризовать только одним параметром − одним углом ω (углом Вика).
Итак, у нас будет
| r(ω) = h-1(pL) lz(βCM)h(p) | (15.51) |
Очевидно, что такое вращение есть просто поворот вокруг оси Y. Самый простой способ это увидеть − посмотреть шаг за шагом. как последовательность операций (15.51) действует на единичные векторы e(y) = (0010) и e(x) = (0100) в направлении осей Y и X соответственно. Очевидно, что при действии на e(y) он не меняется. Поэтому r(ω) = ry(ω), и угол ω проще всего вычислить, посмотрев на результат преобразования, совершаемого над e(x) = (0100). Выполнив последовательность (15.51) над e(x) получаем:
e(x)' = {0, cos θ cos θL + γCM sin θ sin θL, 0, -(m/E) (sin θ cos θL − γCM cos θ sin θL)}.
Видим, что при таком преобразовании e(x) действительно испытывает вращение относительно оси Y на угол ω, и этот угол можно найти из соотношений
|
cos ω = cos θ cos θL + γCM
sin θ sin θL sin ω = (m/E) (sin θ cos θL — γCM cos θ sin θL) 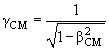 |
(15.52) |
Таким образом, при преобразовании из с.ц.м. в л.с. для частицы с нулевым азимутальным углом имеем:
|
|
(15.53) |
Отметим, что если работать в пространстве 4-скоростей, имеющем (неевклидову!) геометрию Лобачевского, то угол ω можно не только представить достаточно наглядно, но и вполне просто вычислить (см. [88] или [90, 91, 92]). Вывод соответствующих формул можно найти в указанных работах, но для полноты изложения они даны ниже. При этом используются следующие определения (p и E − импульс и энергия частицы)3:
|
tanh(u) = p/E ; tanh(uL)= pL/EL;
tanh(uCM) = βCM.
sin ω/sinh uCM = sin θL/sinh u = sin θ/sinh uL, |
(15.54) |
где фактически используется соотношение pL sin θL = psin θ, и
| cosh uCM = cosh u cosh uL − sinh u sinh uL cos ω. | (15.55) |
Неевклидовость пространства скоростей приводит к неравенству ω < (θ −
θL): в нерелятивистском случае было бы ω = (θ-θL).
Настало время рассмотреть более общий случай, когда частица K
испускается с импульсом p в с.ц.м. при азимутальном угле φ в обеих (с.ц.м.
и л.с.) системах. Можно убедиться, что и в этом случае Вигнеров поворот
спиральности будет даваться оператором ry(ω) и не будет зависеть от
φ.
Весьма часто встречающийся на практике случай − бинарная
реакция A + B → C + D. Обозначим угол рассеяния частицы C в л.с. через θL
а угол вылета частицы отдачи D в л.с. через θR. Тогда угол ω можно
вычислить, используя следующие полезные формулы:
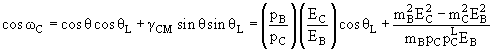 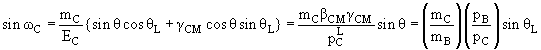 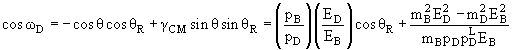 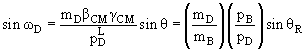 |
(15.56) |
где θ есть угол рассеяния частицы C в с.ц.м.
Для случая упругого рассеяния, когда mB = mD
и mA = mC, угол Вика особенно прост:
| ωD = θR, | (15.57) |
а в случае рассеяния тождественных частиц (например, pp), когда mA = mB, еще проще:
| ωC = θL . | (15.58) |
Наконец, можно убедиться, что при ультрарелятивистских
энергиях угол Вика θC → 0, когда
s → ∞ .
15.2 3π система с изоспином 0
Рассмотрим состояние с тремя пионами с точки зрения изоспина. Необходимо получить состояние с полным изоспином I =0 из трех состояний типа
|
| I = 1, Iz = 1 > = | π+ > | I = 1, Iz = 0 > = | π0 > | I = 1, Iz = -1 > = | π− > |
(15.59) |
Возьмем сначала пару пионов. Состояние из двух пионов
может иметь полный изоспин
I = 0, 1, 2. Далее это состояние складывается с третьим пионом в состояние с
полным изоспином 0. Используем правила сложения угловых моментов для состояний с
изоспином 1:
|
|1,1> =
|1,0> = |1,-1> = |
(15.60) |
Изоскалярное состояние пары пионов:
|
|0,0> =
|
(15.61) |
Т. о. надо сложить состояния | Π > с | π > так, чтобы получить изоскалярное состояние трех пионов. Очевидно, что нужное нам состояние есть
|
|0,0> =
|
(15.62) |
Подставляя в (15.62) выражения из (15.60), получим (11.2)4.
Может возникнуть вопрос: а почему для состояния двух пионов
мы ограничились (15.60)?
Ответ очевиден: складывая два пионных изоспиновых состояния
можно получить состояния с полным изоспином 0,1,2. Но затем их нужно снова
сложить с пионом, т. е. изовектором. Складывая 0 и 1, получим
трехпионное состояние с полным изоспином 1, которое нас сейчас не
интересует. Складывая состояние пары пионов с полным изоспином 2 с пионом, снова
получим не то, что нужно, а именно, 3π - состояния с полным изоспином 1,
2 и 3. Только изовекторное состояние пары пионов может дать, при
сложении с однопионным состоянием, трехпионное состояние с полным изоспином 0.
15.3 Симметрии решений
Всякий закон сохранения связан с проявлением какой-либо
симметрии. Есть различные виды симметрии, например − проявляющиеся в уравнениях
движения. Они достаточно привычны. Однако есть класс симметрии, которым нечасто
уделяется внимание в учебниках. Это − так называемые "симметрии решений"
уравнений движения. Дело в том, что любое решение уравнений движения требует
рассмотрения определенных граничных условий и симметрия решения не обязательно в
точности совпадает с симметрией уравнения именно из-за граничных условий.
Существует прекрасный пример, иллюстрирующий некоторые
аспекты "симметрии решений". Он помогает также понять, что обычно имеется в виду
под "спонтанным нарушением" какой-либо симметрии.
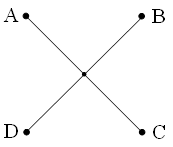 Рис. 15.1. Один из напрашивающихся вариантов прокладки дороги. |
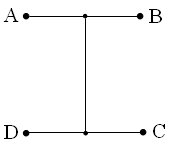 Рис. 15.2. Второй возможный, но явно не кратчайший, вариант прокладки дороги. |
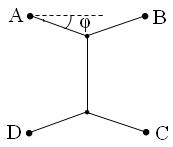 Рис. 15.3. Обобщение предыдущих вариантов прокладки дороги. |
Рассмотрим так называемую "задачу о четырех
городах" [97]. Пусть четыре города (A, В, С, D) расположены в углах
квадрата со стороной 2 ед. Требуется соединить их железной дорогой
наименьшей возможной длины так, чтобы по ней можно было бы проехать
из любого одного города в любой другой.
Задача имеет симметрию квадрата (вращение вокруг центра на
π/2 или на π оставляет расположение городов на плоскости неизменным),
и (по первому впечатлению) решение тоже должно иметь эту симметрию,
например, как на рис. 15.1. Длина железнодорожного пути здесь равна,
очевидно,
4√2 ≈ 5.66 ед. Это
явно меньше, чем в решении рис. 15.2, где длина пути равна 6 ед.
Кроме того, вариант рис. 15.2 имеет не все степени симметрии, что у
квадрата: он переходит сам в себя при вращении не на π/2, а на π.
С другой стороны, оба возможных решения являются предельными
случаями одного и того же варианта, показанного ниже: при φ = π/4
имеем вариант, показанный на рис. 15.1, при φ = 0 − вариант рис.
15.2. Но нужно проверить, действительно ли рис. 15.3 дает решение
задачи (т. е. полная длина дороги в этом варианте минимальна). Это
легко сделать, отталкиваясь от общего варианта. Очевидно, что полная
длина дороги равна
|
|
(15.63) |
Минимум этого функционала находится стандартным способом:
|
|
(15.64) |
то есть вариант, изображенный на рисунке 15.3, дает решение поставленной
задачи при φ = π/6. Но это решение не обладает симметрией исходной задачи!
Вместе с тем, найденное решение все же симметрично
относительно некоторого подмножества группы симметрии квадрата, а именно,
поворотов на угол π.
Вполне очевидно, что данное решение не единственное: если
взять уже уже найденное и повернуть его на <р = π/2, то получим другое решение (длина
пути та же самая и по-прежнему минимальна). То есть, все множество решений
сохраняет симметрию исходной задачи, но отдельное решение - нет; все решения
можно получить из одного, найденного каким-то образом, применением к нему
преобразований, оставляющих квадрат неизменным. Это и есть проявление т. н. "скрытой
симметрии" − когда симметрия решения ниже симметрии задачи, но множество всех
решений имеет группу симметрии задачи.
Наконец, как только сделан выбор из двух решений, дающих
минимальную длину дороги, и дорога оказалась построенной, исходная симметрия
задачи разрушается и дальнейшая "жизнь" рассматриваемой системы проходит при
меньшей степени симметрии. Это и понимается под "спонтанным нарушением"
симметрии; спонтанность − в том, какое именно из двух решений берется. (Один из
самых известных примеров "спонтанного" выбора − Буриданов пример об осле и двух
вязанках сена.)
Если в рассмотренной задаче откажемся от условия
симметричного расположения городов и разрешим им быть расположенными как угодно,
(т. е. не обязательно симметрично) то получим проблему, известную как " задача
Штайнера" или " задача о кратчайшей сети".
Можно убедиться, что дерево, представляющее кратчайшую сеть,
имеет следующие главные свойства:
- из каждой развилки выходят ровно три отрезка, каждые два из которых образуют угол в 120°;
- из каждого города выходит один, два или три отрезка, причем если выходит два, то угол между ними не меньше 120°, а если три − то ровно 120°;
- никакие отрезки кратчайшей сети не образуют замкнутую ломаную;
- число развилок по крайней мере на две меньше числа городов.
Подробнее об этом круге проблем см. в обзоре А.М. Балдина и А.А. Балдина [98], а также − в лекциях [97].
15.4 "Инвариантная масса"?
В школьных учебниках (да и в других, более серьезных
книгах) можно иногда прочесть, что "масса тела зависит от его скорости", или
найти задачи типа "чему равна масса фотона, если его энергия
10 МэВ" и т. п. О том, почему подобные утверждения неправильны, сказано в статье
Л.Б.Окуня [6].
Бессмысленность термина "инвариантная масса" можно увидеть
непосредственно из следующего наблюдения. Известно, что 4-вектор
энергии-импульса
![]() = (Е, р),
имеет 4 компоненты, причем энергия -одна из них, и эта компонента преобразуется
при лоренцевых вращениях в импульсном пространстве. "Мерой длины" 4-вектора
= (Е, р),
имеет 4 компоненты, причем энергия -одна из них, и эта компонента преобразуется
при лоренцевых вращениях в импульсном пространстве. "Мерой длины" 4-вектора
![]() является
скаляр
является
скаляр
![]() 2 =
m2: квадрат массы частицы; она не меняется при таких вращениях (т. е.
инвариантна по определению!) Соответственно, раз не существует "неинвариантной"
массы, не имеет смысла говорить и об "инвариантной" массе.
2 =
m2: квадрат массы частицы; она не меняется при таких вращениях (т. е.
инвариантна по определению!) Соответственно, раз не существует "неинвариантной"
массы, не имеет смысла говорить и об "инвариантной" массе.
Достойно сожаления, что даже в такой полезной книге как [3].
систематически употребляется бессмысленное (а следовательно, бесполезное)
выражение "инвариантная масса". В некотором роде такое выражение даже вредно,
так как искажает суть дела.
(1) Сравните "локальное" и "глобальное" калибровочное преобразование в случае электромагнитного поля, например.
(2) Напомним, что рассматриваемые здесь вопросы хорошо изложены в литературе и для более исчерпывающего их рассмотрения стоит обратиться к соответствующим монографиям или обзору [88]
(3) Ср. с определением быстроты, данным ранее.
(4) Проверьте последнее утверждение.