|
|
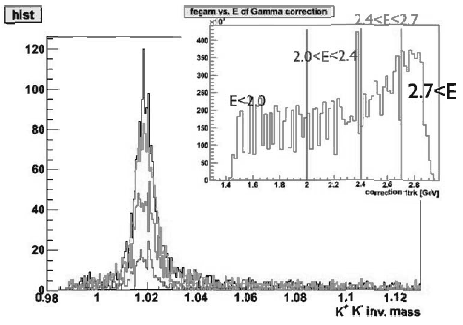
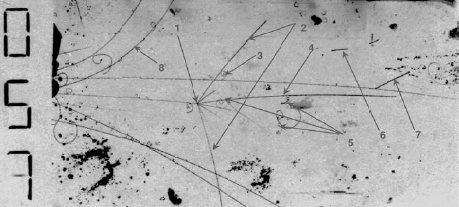
Рис. 16.1. Распределения событий по эффективной массе пары − мезонов и по энергии фотонов пучка, полученные при анализе данных по фоторождению мезонов на протонах. В эксперименте использовалась жидко-водородная мишень в пучке "меченых" фотонов. |
10. При анализе данных, накопленных в эксперименте по
фоторождению ф мезонов в реакции p (γ,![]() )Х
с использованием пучка "меченых" фотонов, аспирант попытался ответить на вопрос
о количестве зарегистрированных случаев этой реакции при разных энергиях фотонов
и получил распределения, показанные на рисунке 16.1. На его нижней панели
показано распределение по эффективной массе пары
)Х
с использованием пучка "меченых" фотонов, аспирант попытался ответить на вопрос
о количестве зарегистрированных случаев этой реакции при разных энергиях фотонов
и получил распределения, показанные на рисунке 16.1. На его нижней панели
показано распределение по эффективной массе пары
K-мезонов. Пик в этом распределении отвечает каонным парам от распада
![]() →
К+К−. На верхней панели рисунка 16.1 показано
распределение событий в зависимости от энергии фотона. Аспирант сделал
утверждение, что события в этом распределении те же самые, что и в распределении
по эффективной массе каонной пары. Верно ли это утверждение? Что может вызвать
сомнение в его истинности?
→
К+К−. На верхней панели рисунка 16.1 показано
распределение событий в зависимости от энергии фотона. Аспирант сделал
утверждение, что события в этом распределении те же самые, что и в распределении
по эффективной массе каонной пары. Верно ли это утверждение? Что может вызвать
сомнение в его истинности?
11. Представьте в явном виде нерелятивистский предел соотношений
(3.22) (т. е. предел β << 1,
γ ≈ 1):
![]() =
(u1 · u2)
=
(u1 · u2)
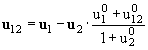
(NB:
![]() = E1/m1
= γ1, u1 = p1/m1 = γ1β1
и т. д.).
= E1/m1
= γ1, u1 = p1/m1 = γ1β1
и т. д.).
12. Переменная Мандельстама s имеет, как известно, смысл полной энергии в системе центра масс сталкивающихся частиц, то есть
s = (![]() a
+
a
+
![]() b)2
= (E*a + E*b)2,
b)2
= (E*a + E*b)2,
где звездочка в верхнем индексе, как всегда, помечает кинематические величины в системе центра масс реакции. Получите формулы, выражающие E*a и E*b через инвариант s и массы частиц.
13. (а) Получите формулу (3.29)
для импульса частиц a и b в системе центра масс. (Ь) Получите аналогичную
формулу для импульса снаряда (частица a) в системе покоя частицы b (лабораторная
система). Какой практический вывод вы бы сделали из сравнения полученной вами
формулы с формулой (3.29)? Проверьте этот вывод, перейдя в "антилабораторную"
систему, или систему покоя частицы a, и вычислив в ней импульс частицы b.
Напоминание. " Функция треугольника"
λ (x,y,z) определена как λ (x,y,z) = x2 + y2
+ z2 − 2xy − 2xz − 2yz = (x − y − z)2 − 4yz.
14. Выведите формулы (3.32), выражающие скорость (и гамма-фактор) системы центра масс через инварианты и массы частиц. Вторые части этих формул легко получить в пределе больших (по сравнению с массами) значений s.
15. Для рассеяния a + b → a' + b' частиц одинаковых масс (ma = mb = m) сравните скорость системы центра масс βcm (относительно лабораторной системы, где частица b покоится) со скоростью частицы a (или b) β* в системе центра масс.
16. В реакции a + b → с + d конец вектора, изображающего лабораторный импульс частицы с, на плоскости (px,py=0,pz) (ось Z направлена по импульсу пучка) лежит на эллипсе (т. н. "эллипс импульсов"). Покажите, что экстремальные значения лабораторного импульса частицы с задаются формулами (3.38), где β* есть скорость частицы с в системе центра масс:
p1 = (0, 0, γcmE*(βcm − β*)) , p2 = (0, 0, γcmЕ*(βcm + β*)) .
17. Проведите кинематический анализ реакции n(K,π)Λ и дайте ответы на следующие вопросы:
- имеет ли она порог в физической области энергий и каков он;
- если K-мезон имеет импульс pK (разумеется, выше порога) то каковы величины минимально возможного и максимально возможного импульсов Λ-гиперона?
- Может ли в этой реакции π-мезон вылететь "назад" в лабораторной системе отсчета?
- Может ли в этой реакции Λ-гиперон вылететь "назад" в лабораторной системе отсчета?
- Постройте график зависимости минимально возможного импульса Λ-гиперона от импульса pK.
18. Зная, что
![]() =
=
![]()
pz = γcmpz* + γcmβcmE*
E = γcmE* + γcmβcmpz*,
свяжите угол вылета частицы с в лабораторной системе отсчета с ее углом вылета в системе центра масс и докажите, что
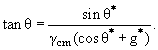 g* = βcm/β*.
g* = βcm/β*.
19. Выразив, например, энергию частицы с в с.ц.м. через
продольный импульс и энергию в лабораторной системе, можно получить уравнение,
определяющее величину импульса этой частицы в лабораторной системе отсчета в
зависимости от угла ее вылета, т. е. найти функцию
p(θ):
Е* + βcmγcmp cos θ = γcm (p2 + m2)1/2.
Решите это уравнение (см. (3.40)).
20. Для бинарной неупругой реакции типа μ + m → μ + М, где μ − масса снаряда, m -− масса мишени, М − масса частицы, в которую после рассеяния превратилась частица-мишень, выведите формулу для tmin, считая, что s >> mi2 (mi − массы частиц, участвующих в реакции).
16.3 Задачи к лекциям 5 и 6
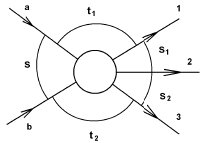
21. (а) Покажите, что векторы l, m, n, определенные в (16.1), попарно ортогональны друг к другу. Выполните аналогичную проверку для ортов, определенных согласно формулам (16.3).
| l = (kƒ + ki) / |kƒ + ki|, m = (kƒ − ki) / |kƒ − ki|, n = (kƒ × ki) / |kƒ × ki|, | (16.1) |
где ki и ki есть единичные векторы, направленные вдоль импульсов начальной и рассеянной частиц, соответственно. Векторы l, m и n, определенные в (16.1), удовлетворяют соотношениям
| l = m×n, m = n×l, n = l×m. | (16.2) |
Существует также другое определение базисных ортов
| l = (kƒ + ki) / |kƒ + ki|, m = (ki − kƒ) / |ki − kƒ|, n = (kƒ × ki) / |kƒ × ki|, | (16.3) |
При таком определении они удовлетворяют соотношениям
| l = n×m, m = n×l, n = m×l. | (16.2) |
(b) Проверьте формулы (16.2) и (16.4).
(с) Какие из этих двух троек ортов соответствуют правовинтовой системе координат? Если только одна, то какой системе соответствует другая тройка?
22. Объясните, почему в связи с несферичностью дейтрона говорят только о D-состоянии в нерелятивистской волновой функции дейтрона.
|
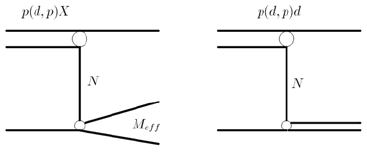
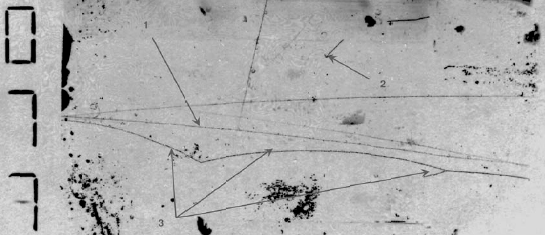
Рис. 4.З. Простейшие (полюсные) диаграммы для процессов развала (фрагментации) дейтронов на протонах и упругого рассеяния d(p,d)p "назад" в с.ц.м. Классификация характерных кинематических областей: упругое обратное рассеяние, развал дейтрона без образования других частиц, развал дейтрона с возможностью рождения других частиц. |
23. В "спектаторном" механизме фрагментации дейтрона предполагается, что основной вклад в амплитуду реакции дает левая диаграмма рис. 4.3.
(а) Рассмотрите кинематику вершины "развала" дейтрона на систему "протон+нейтрон" в системе покоя дейтрона и получите формулу ((4.11)). Найдите относительный импульс нейтрона (т. е. импульс, взятый в системе покоя протона-спектатора) в случае, когда нейтрон находится "на массовой поверхности", т. е. выполняется соотношение En2 − qn2 = mn2.
(б) Покажите, что условие:
![]() ≥ 0
влечет за собой ограничение (4.12) на величину относительного импульса:
≥ 0
влечет за собой ограничение (4.12) на величину относительного импульса:
q ≤ 3mN/4.
24. Для упругого рассеяния типа 1+2 → 1' + 2' найдите связь лабораторного угла рассеяния с углом рассеяния в системе центра масс. Выпишите формулу, связывающую тангенсы этих углов (или угла рассеяния в л.с. с половинным углом рассеяния в с.ц.м.).
25. Реакция n(K,π)Λ с начала 1960-х годов, после появления
статьи [60], широко используется в экспериментах по изучению гиперядер,
благодаря особенности ее кинематики, впервые замеченным М. И. Подгорецким.
Именно: при определенном значении лабораторного импульса K-мезона,
образовавшаяся
Λ-частица оказывается покоящейся в лабораторной системе. Найдите это "магическое"
значение импульса K-мезона. Проанализируйте полученную общую формулу. В реакциях
какого типа могут быть подобные особенности?
26. Рассмотрите реакцию фоторождения мезона на покоящемся в
лабораторной системе нуклоне (массу нуклона обозначим как M): γ + N →
![]() + N.
Определите, при какой энергии фотона Eγ (и при каком соотношении
между массами мезона
+ N.
Определите, при какой энергии фотона Eγ (и при каком соотношении
между массами мезона
![]() и нуклона)
мезон в этой реакции может оказаться покоящимся в лаборатории.
и нуклона)
мезон в этой реакции может оказаться покоящимся в лаборатории.
16.4 Задачи к лекциям 7 и 8
27. Докажите, что эффективная масса группы фотонов, летящих в одном направлении, равна нулю. (Г.И.Копылов)
28. Докажите, что если в какой-нибудь одной системе отсчета направления движения двух фотонов совпадают, то они совпадают в любой другой системе отсчета. (Г.И.Копылов)
29. Для распада 0 → 1 + 2 частицы 0 с массой M0 на частицы 1 и 2 с массами m1 и m2 соответственно, выпишите формулы для полных энергий частиц 1 и 2, их кинетических энергий, а также отношения этих кинетических энергий.
30. Пусть имеется в лабораторной системе "родительская" частица
0 с 4-импульсом
![]() 0 =
(E0,p0) (выберем направление оси Z по направлению
импульса p0), и пусть она распадается с вылетом распадной частицы 1 с
4-импульсом
0 =
(E0,p0) (выберем направление оси Z по направлению
импульса p0), и пусть она распадается с вылетом распадной частицы 1 с
4-импульсом
![]() 1 =
(E1,p1). Под углом вылета этой распадной частицы
будем понимать угол между p1 и направлением оси Z. Чтобы его
найти, достаточно вычислить инвариант (
1 =
(E1,p1). Под углом вылета этой распадной частицы
будем понимать угол между p1 и направлением оси Z. Чтобы его
найти, достаточно вычислить инвариант (![]() 0
·
0
·
![]() 1)
в системе покоя распадающейся частицы и в лабораторной системе:
1)
в системе покоя распадающейся частицы и в лабораторной системе:
(![]() 0
·
0
·
![]() 1)
= E0E1 − p0p1 = E0E1 −
p0p1 cosθ1 = E0*E1* .
1)
= E0E1 − p0p1 = E0E1 −
p0p1 cosθ1 = E0*E1* .
Поскольку энергия и импульс распадающейся частицы известны, а энергия распадной частицы связана с ее импульсом и массой, то соотношение (6.4) можно считать уравнением, связывающим импульс распадной частицы с ее углом вылета. Покажите, что искомое решение уравнения (6.4) дается формулами (6.5) и (6.6):
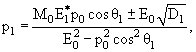 |
(6.5) |
где
|
|
(6.6) |
31. Для распада 1 → 2 + 3 при условии, что массы частиц 2 и 3 равны нулю (пример: распад π0 на два фотона) выведите соотношение
![]()
и покажите с его помощью, что минимальный угол разлета
![]() получается, когда θ2 = θ3 (симметричные условия). Чему
равен синус этого минимального угла? (См. также задачу 34.)
получается, когда θ2 = θ3 (симметричные условия). Чему
равен синус этого минимального угла? (См. также задачу 34.)
32. Можно связать с углом вылета распадной частицы и ее энергию; найдите это выражение сами и сравните с формулой (23) гл. II (параграф 2) в книге Г.И.Копылова [2].
33. Под углом разлета ψ(E1) распадных частиц в
распаде 0 → 1 + 2 "на лету", когда в лабораторной системе 4-импульс
распадающейся частицы равен (E0,p0), будем понимать
угол между импульсами p1 и p2 при энергии
распадной частицы 1 равной E1.
Проделайте самостоятельно выкладки, приводящие к формулам
(6.12)-(6.14):
|
|
(6.12) |
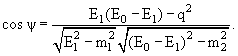 |
(6.13) |
причем предельные значения E1, очевидно, отвечают вылету частицы 1 в системе покоя 0"назад" (E1,min) и "вперед" (E1,max). Соответственно,
|
|
(6.14) |
34. Продолжая анализ распада 0→ 1 + 2 "на лету", в случае, когда распадные частицы - фотоны, выведите формулы (6.16) и (6.17):
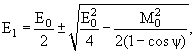 |
(6.16) |
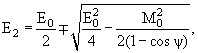 |
(6.17) |
Проанализируйте эти формулы: всякие ли углы разлета разрешены? Как найти минимальный угол разлета?
35. Для упругого рассеяния типа 1 + 2 → 1' +2' найдите связь лабораторного угла рассеяния с углом рассеяния в системе центра масс. Выпишите формулу, связывающую тангенсы этих углов (или угла рассеяния в л.с. с половинным углом рассеяния в с.ц.м.).
36. 1) Пусть рассматривается реакция a + T → c + X, имеющая порог при
ненулевом импульсе снаряда a с ненулевой массой, который падает на покоящуюся в
л. с. мишень T. Частица c регистрируется, а система X имеет минимально возможную
массу M (недостающую массу) и не регистрируется. Дайте аналитический вывод
соотношения между массой мишени и массой регистрируемой частицы, при выполнении
которого всегда существует такое значение импульса снаряда, что условие "безотдачности"
выполняется (т. е. импульс частицы c в л. с. равен нулю).
2) Справедливо ли это соотношение, если снаряд является фотоном?
16.5 Фазовый объем
37. Проделайте самостоятельно выкладку, дающую последнее равенство формулы (9.15):
|
|
(9.15) |
38. Покажите, что
(а) вблизи порога реакции, где √s
мало отличается от суммы масс частиц конечного состояния, фазовый объем растет
от нуля (который имеет место, когда √s
равен пороговому значению sthresh) так, как показано в формуле
(9.24):
|
|
(9.24) |
где
![]() называется " превышением над порогом";
называется " превышением над порогом";
(б) в ультрарелятивистском пределе (когда всеми массами можно
пренебречь), справедлива формула (9.25):
|
|
(9.25) |
39. Рассмотрите реакции (а) n + p → M + d и (b) n + p → M + n + p вблизи порога рождения мезона M в них. Сравните фазовые объемы этих реакций (Ra2 и Rb3) при одинаковом превышении над соответствующими порогами, получив в нерелятивистском пределе выражение для отношения Ra2/Rb3.
40. Распад Λ -частицы может идти как по каналу Λ → p + π−, так и по каналу Λ → n + π0. Вычислите отношение фазовых объемов для распадов по этим каналам.
41. Объясните характер распределения событий на рис. 16.2 и рис. 16.3, взятых из статьи [66]:
- Почему на левой панели есть один изолированный "островок", отделенный незаселенной областью от области, ограниченной "гребнем" с высокой концентрацией событий?
- Почему на правой панели есть области с очень низкой концентрацией событий?
- События какого типа группируются в "островок" в форме эллипса?
- Почему этот островок погружен в область, засеянную событиями?
- Какие причины могли бы обусловить низкую концентрацию событий возле линии p1 = p2?
- Какие физические особенности, помимо перечисленных, вы заметили на распределении, показанном на правой панели?
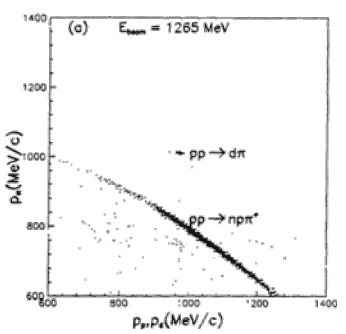 Рис. 16.2. Данные из [66] по реакций неупругого pp взаимодействия. Распределение по импульсам пиона (ось абсцисс) в совпадении с тяжелой положительно заряженной частицей; ее импульс отложен по оси ординат. |
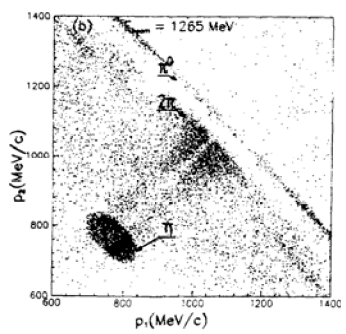 Рис. 16.3. Данные из [66]. Распределение по импульсам протонов для событий с регистрацией не менее 2-х протонов в совпадениях. По осям абсцисс и ординат отложены импульсы каждого из протонов. |
42. Почему на диаграмме Арментероса-Подолянского (см. рис. 7.1) для V0-частицы, распадающейся на две заряженных частиц, распределения событий от распада каонов и от распада Λ0 не только имеют разный характер, но и разные значения максимального поперечного импульса?