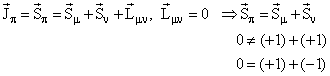Спиральность и четность нейтрино

    Перед рассмотрением понятия спиральности нужно ввести понятие поляризации частицы. Поляризация частицы — это состояние частицы с преимущественной ориентацией ее спина вдоль выбранного направления. При поперечной поляризации спин частицы перпендикулярен ее импульсу. При продольной (круговой) поляризации спин направлен вдоль импульса частицы.
    В зависимости от того, как направлен спин частицы относительно её импульса при продольной поляризации, различают правую и левую поляризацию. Правополяризованной считается частица, спин которой направлен по импульсу, левополяризованной − спин которой направлен против импульса. Для характеристики взаимного направления спина и импульса частицы используют понятие спиральности.
Спиральностью h называют величину:

где S – спин частицы, p – ее импульс.
    Принято называть правополяризованной частицу, имеющую положительную спиральность (h=+1), а левополяризованной – имеющую отрицательную (h=-1) спиральность. Еще говорят о правовинтовой и левовинтовой спиральности частицы соответственно.
    Как следовало из закона, который до 1957 г. считался неоспоримым для нейтрино, - закона сохранения четности, в составе любого пучка нейтрино половина частиц имеет правое вращение по отношению к направлению движения, а другая половина - левое. В соответствии с этим законом во всех физических явлениях должна иметь место строгая "зеркальная" симметрия, так что в природе не должны происходить явления, в которых правое преобладает над левым и наоборот. В нашем случае закон сохранения четности запрещает испускание продольно поляризованных нейтрино, т.е. нейтрино, имеющих, скажем, преимущественно левое вращение по отношению к направлению движения.
    Говоря другими словами, до открытия несохранения чётности в бета-распаде считалось, что нейтрино описывается волновой функцией, являющейся решением уравнения Дирака, и имеет четыре состояния, соответствующие четырём линейно-независимым решениям: два с проекцией спина на импульс (спиральностью) J = —1/2 — левое (левовинтовое) нейтрино и левое антинейтрино и два с J = + 1/2 — правое (правовинтовое) нейтрино и правое антинейтрино. Теория нейтрино, предполагающая существование четырёх состояний, называется четырёхкомпонентной, а двух состояний — двухкомпонентной. Примерами двухкомпонентного нейтрино является майорановское нейтрино (нейтрино тождественное антинейтрино) и спиральное нейтрино.

Рис. 13. Спиральность нейтрино и антинейтрино

    В 1958г. было экспериментально показано, что спиральность нейтрино всегда отрицательна, а спиральность антинейтрино – всегда положительна. В природе не наблюдается правополяризованных нейтрино и левополяризованных антинейтрино.
    Данный эксперимент был проведен в Брукхейвене группой М. Гольдхабера.  Было сделано прямое измерение спиральности электронного нейтрино, испускаемого в процессе ¹⁵²Eu (e⁻,ν_e)¹⁵² Sm^*, и найдено, что с вероятностью, близкой к 100%, ν_e обладает левовинтовой спиральностью.
    В этом эксперименте, задача непосредственного определения спиральности нейтрино была сведена к определению спиральности фотона, участвовавшего наряду с нейтрино в процессе радиоактивного распада ядра. Был использован е-захват возбужденного состояния  изотопа ¹⁵² Eu*  (Т_1/2 =  9.3 часа) с энергией 45 кэВ и спином-четностью J^p = 0⁻. Радиоактивный препарат ¹⁵² Eu 1 испускает в результате К-захвата нейтрино. Образующееся возбуждённое ядро ¹⁵²Sm^*(J^p = 1⁻) с энергией 0.961 Мэв довольно быстро испускает гамма-квант с аналогичной энергией, превращаясь в стабильное ядро ¹⁵²Sm(J^p = 0⁺).

Рис. 14. Схема распада ядра ¹⁵² Eu из изомерного состояния

    Т.к. данный е-захват является разрешенным переходом гамов-теллеровского типа (орбитальные моменты частиц равны нулю), закон сохранения момента импульса для данной реакции выглядит так:

.

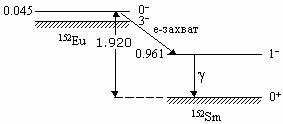
    Видно, что спины возбужденного ядра самария и нейтрино антипараллельны. Поскольку продукты распада разлетаются в противоположные стороны по закону сохранения импульса, то нейтрино и получившее отдачу ядро самария будут иметь одинаковую спиральность (положительную или отрицательную). Возбужденное ядро ¹⁵²Sm^* за время 7х10^-14 с распадается с образованием фотона. Задачей эксперимента было детектировать те фотоны, которые испускаются в направлении движения ядра отдачи, т.к. они имеют такую же спиральность, что и ядро, а, следовательно, такую же, как и нейтрино.
   Отбор "нужных" фотонов проводился с помощью их резонансного рассеяния (резонансной флуоресценции) на мишени.

    В этой цепочке процессы, отмеченные стрелками , относятся к стадии резонансной флуоресценции. Фотоны испускаемые возбужденными ядрами ¹⁵²Sm резонансно возбуждают ядра самария мишени, которые в свою очередь испускают фотоны, которые нужно регистрировать. Таким образом регистрируются только те события, для которых выполнено условие резонансной флуоресценции.
    Ядерная резонансная флуоресценция возможна, если скомпенсировать эффект отдачи ядер, снижающий энергию испускаемых фотонов до величины достаточной для их поглощения теми же ядрами, причем отдача ядра должна быть скомпенсирована дважды – при испускании ядром фотона и затем при его поглощении.
    Энергия, освобождающаяся при е-захвате и последующей эмиссии фотона, равна Q_e = 1.920 МэВ (см. рис. 14) и практически поровну делится между нейтрино и фотоном (энергия фотона 0,961 МэВ). Таким образом, для этого перехода и в той кинематике, когда нейтрино и фотон последовательно оставляют ядро, вылетая в противоположных направлениях, эффекты отдачи ядра от них оказываются почти полностью скомпенсированными.
    Теперь посмотрим как обстоит дело с компенсацией энергии отдачи при возбуждении ядер самария в мишени. Собственная (естественная) ширина уровня 1- с энергией 0.961 МэВ равна:

G = ћ/τ ≈ 10^-2 эВ.

    Энергия отдачи ядра самария при поглощении фотона с энергией Е = 0.96 МэВ можно оценить с помощью формулы

    Таким образом энергия отдачи ядра существенно больше собственной ширины уровня и, следовательно, последняя скомпенсировать энергию отдачи не может. Однако, доплеровское уширение уровня ядра 0.961 МэВ оказывается достаточно большим, чтобы для значительной части фотонов выполнялось поглощения ядрами мишени. Дело в том, что атомы (и ядра) источника и мишени находятся в тепловом движении. Поэтому фотоны испускаются ядрами, двигающимися с различными тепловыми скоростями и в различных направлениях. Распределение по скоростям является максвелловским. В результате линия 0.961 МэВ существенно уширяется, и её форма становится отличной от естественной (брейт-вигнеровской). В большинстве случаев форма этой линии гауссова с шириной на половине высоты равна:

где Е − средняя энергия фотона, k − постоянная Больцмана , Т − абсолютная температура, М − масса ядра. Это означает, что высокоэнергичный участок доплеровски уширенной линии 0.961 МэВ обеспечивает возможность резонансного поглощения ядрами мишени значительного числа фотонов, вылетающих из источника ¹⁵²Eu в сторону противоположную вылету нейтрино и, следовательно, идентификацию этих фотонов. В этом процессе способны участвовать только нужные для идентификации спиральности нейтрино фотоны, испускаемые возбужденными ядрами самария, движущиеся в направлении противоположном испущенным нейтрино.

Рис. 15. Схема эксперимента М. Гольдхабера

    Рассмотрим схему регистрации фотонов. Фотон, пройдя через магнитный анализатор (2), представляющий собой намагниченное железо, для определения круговой поляризации гамма-квантов, испытывает резонансное рассеяние на ядрах ¹⁵²Sm(J_p =0+) в кольцевом рассеивателе из Sm₂O₃ (3). Детектор фотонов - сцинтилляционный счетчик NaJ(Tl) (4)-  могли достигать лишь те фотоны, которые, во-первых, проходили через магнит и, во-вторых, испытали резонансное рассеяние в кольцевом рассеивателе, окружавшем детектор. Прямое направление от источника ¹⁵²Eu на детектор перекрывалось свинцовым фильтром (5), исключавшим попадание на детектор фотонов без предварительного их резонансного рассеяния мишенью. Часть фотонов, достигших детектора, испытывала комптоновское рассеяние в материале магнита (Fe). Два из 26 электронов атома железа, находящихся на внешней 4d-оболочке, поляризуются при намагничивании. Сечение комптоновского рассеяния больше, если электроны и фотоны имеют противоположную поляризацию. Таким образом, измеряя скорость счета детектора фотонов при разных ориентациях магнитного поля, можно определить знак круговой поляризации фотонов, а значит и спиральность нейтрино.
    Сцинтилляционный детектор в эксперименте считал число гамма-квантов N₊ и N₋, рассеянных при направлениях магнитного поля по и против движения нейтрино. Теоретическое значение

 (+0.025) для левовинтовой и (-0.025) для правовинтовых спиральностей нейтрино. Экспериментально полученное значение равно +0.017 ± 0.003, что дает значение спиральности
h =-1.0±0,3. А этот результат согласуется со 100%-ной левовинтовой спиральностью нейтрино в случае учета всех возможных эффектов деполяризации гамма-квантов. Схема эксперимента изображена на рисунке 15.
    Отсутствие правополяризованных нейтрино говорит о том, что для нейтрино не инвариантно относительно пространственного отражения (операции перехода от правой системы координат к левой). А инвариантность относительно операции пространственного отражения является необходимым условием для сохранения четности у нейтрино. Следовательно, нейтрино, рождающиеся и участвующие только в слабых процессах, являются хорошим доказательством несохранения четности в слабых взаимодействиях. Этот факт не позволяет нам присвоить нейтрино какую-либо определенную внутреннюю четность. 
    Левоспиральность нейтрино (и правоспиральность антинейтрино) можно объяснить только исходя из безмассовости нейтрино (m_ν = 0). Т.к. для массовой частицы всегда существует преобразование Лоренца, которое изменяет направление импульса частицы на противоположное, при этом, естественно, не меняя направление спина частицы. А это привело бы к тому, что в новой системе отсчета нейтрино стало бы правоспиральным и совпало бы с антинейтрино, что, в свою очередь, привело бы к несохранению лептонного заряда. Таким образом, массовость нейтрино приведет к нарушению закона сохранения лептонного заряда. Этот вопрос будет подробнее рассмотрен при описании нейтринных осцилляций.
    В 1956 г. Ли Дзундао и Янг Чженьнин выдвинули гипотезу, что при слабых взаимодействиях не только пространственная, но и зарядовая симметрия не имеют места. В многочисленных экспериментах обнаружились явления, в которых эти законы явно нарушаются, но обязательно оба сразу. В частности, несохранение четности в слабых взаимодействиях подтверждено экспериментально в 1957 г. By Цзяньсюн в Колумбийском университете (США) в опыте, методика которых была разработана Ли Дзундао и Ян Чженьнином.
    Подготовка к эксперименту началась в 1956 г. и заняла шесть месяцев. By поместила радиоактивный кобальт внутрь электромагнита и охладила его до температуры, близкой к абсолютному нулю, чтобы свести к минимуму влияние теплового движения частиц. В опыте изучался бета-распад строго поляризованных (с определенным направлением спина) атомов ⁶⁰Co:

⁶⁰Co → ⁶⁰Ni + e⁻ + _e

     Электроны могли испускаться либо в направлении, совпадающем с направлением спина ядра кобальта  - к северному полюсу магнита, либо в противоположном направлении – к южному полюсу магнита. Эти два состояния электрона переходят друг в друга при операции пространственного отражения: направление импульса меняется на противоположное при неизменном направлении спина. Если бы при бета-распаде, определяющемся слабым взаимодействием, четность сохранялась, то в направлении северного и южного полюсов магнита вылетало бы равное число испускаемых электронов. Это можно наглядно показать, представив себе пространственное отражение как зеркальное отражение в плоскости x0y и поворот на 180⁰ вокруг оси z. Пусть электрон со спином, т.е. осью вращения, направленным к зеркалу, летит по направлению к зеркалу. Тогда в зеркале направление спина не изменится из-за того, что спин – аксиальный вектор, а направление движение изменится на противоположное из-за того, что импульс – это линейный вектор. Т.е. частица и ее зеркальное отражение не совпадают, а в этом случае для сохранения симметрии необходимо, чтобы одинаковое число частиц испускалось в противоположных направлениях. By обнаружила, что больше электронов вылетает в направлении, в противоположном направлению спина ядра, и, следовательно, четность не сохранялась.
    За свои теоретические работы Ли Дзундао и Ян Чженьнин в 1957 г. получили Нобелевскую премию.
    Все вышеперечисленные факты легли в основу 2-х компонентной теории  спирального нейтрино, которая была создана  лауреатом Ленинской и Нобелевской премий Львом Давидовичем  Ландау и независимо от него пакистанским физиком А. Саламом. Согласно ей, что в природе существует более глубокая симметрия, которую Ландау назвал комбинированной инверсией. Для спирального двухкомпонентного нейтрино операция пространственной инверсии Р и операция зарядового сопряжения С (переход от частицы к античастице) каждая в отдельности не имеет физического смысла, так как переводит реальное нейтрино (или антинейтрино) в несуществующее физически состояние с неправильной спиральностью. Физический смысл имеет только произведение этих операций — так называемая комбинированная инверсия (CP), превращающая реальное нейтрино в реальное антинейтрино с противоположной спиральностью. Согласно данной теории нейтрино безмассово и 100 % поляризовано.

Рис. 16. Пространственное отражение нейтрино. При отражении в зеркале (пространственной инверсии) левое нейтрино переходит в несуществующее состояние правого нейтрино (а). Реальное состояние получается при одновременном (с отражением) переходе от частицы к античастице, при этом левое нейтрино переходит в правое антинейтрино (б).

    Измерения спиральности мюонных нейтрино в распадах показали, что ν_μ тоже имеет левовинтовую спиральность. Было также установлено, что _е и _μ также имеют правую спиральность.
    Этих опытов, однако, недостаточно для подтверждения теории двухкомпонентного нейтрино. Окончательным доказательством двухкомпонентности нейтрино являются опыты Райнеса по измерению сечения захвата антинейтрино: сечение, в соответствии с двухкомпонентной теорией, оказалось в 2 раза выше, чем рассчитанное по четырёхкомпонентной теории. Хотя все проведённые с нейтрино опыты не позволяют исключить майорановский вариант  двухкомпонентного нейтрино, теория спирального двухкомпонентного нейтрино более предпочтительна, так как допускает введение лептонных чисел L_e и L_μ, посредством которых удаётся получить все необходимые запреты в процессах с участием лептонов. Спиральная двухкомпонентная теория является логически более стройной и «экономной», так как из неё естественно вытекает равенство нулю массы и магнитного момента нейтрино.
    Спиральность позволяет объяснить такое наблюдаемое явление, как преобладание мюонного канала распада (*) перед электронным (**) в реакции распада пиона:

π⁺ → μ⁺ + ν_μ (*),       π⁺ → е⁺ + ν_е (**)

    Этот факт на первый взгляд является удивительным, поскольку не запрещенный законами сохранения распад с образованием позитрона идет со значительно большим энерговыделением. Т.к. масса позитрона меньше массы мюона в 207 раз, то энергия распада Q в этом случае также существенно выше. А, как известно, при прочих равных условиях наиболее вероятна реакция с большей энергией распада, т.к. возможно большее число состояний образовавшихся частиц – больший объем фазового пространства. Однако по какой-то причине такой распад происходит в 10⁴ раз реже.

Таблица .4. Каналы распада π⁺- мезона (τ = 2.6·10^-8 с)

Каналы распада	Относительная вероятность, %
μ+νμ	99.988
μ+νμγ	2.0·10-4
е+νе	1.2·10-4
е+νеγ	1.6·10-7
е+νеπ0	1.0·10-8
е+νее+е−	3.2·10-9
е+νеν	< 5.0·10-6

    Для качественного объяснения подавления электронного канала распада достаточно принять во внимание экспериментально установленный факт, что е⁺ и μ⁺ рождаются в слабых процессах со спиральностью h = v/c, т.е. все рождающиеся е⁺ и μ⁺ должны быть правополяризованными. Эту поляризацию можно условно назвать «правильной». Соответственно 1-v/c положительно заряженных лептонов будут левополяризованными, т.е. поляризованными «неправильно». Как уже говорилось, нейтрино может иметь только левую поляризацию. Спин пиона равен нулю, поэтому распад с образованием «правильно» поляризованных е⁺ и μ⁺, имеющих спин, направленный туда же, куда и спин нейтрино,  запрещен законом сохранения углового момента:

    Возможность вылета лептонов с ненулевым относительным орбитальным моментом запрещена, из-за малости радиуса действия R слабых сил, ответственных за данный распад (p×R ≥ L_μν). Поэтому распад пиона идёт с «неправильно» поляризованными е⁺ и μ⁺, а доля таких распадов равна 1-v/c. Можно сказать, что «неправильная» поляризация навязана мюону и позитрону нейтрино.

Рис. 17. Распад π⁺- мезона: спины и импульсы частиц.

    Так как в распаде, идущем по электронному каналу, позитроны ультрарелятивистские (из-за их малой массы), то для них v/c ~ 1, и 1-v/c ~0. В распаде по мюонному каналу мюоны нерелятивистские, следовательно, для них v/c относительно мало, а 1-v/c соответственно довольно велико. Т.е. вероятность рождения «неправильно» поляризованных мюонов значительна. Поэтому вероятность распада с образованием мюона во много раз превосходит вероятность распада образованием электрона (позитрона).
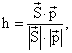