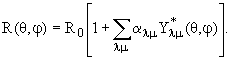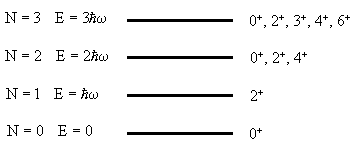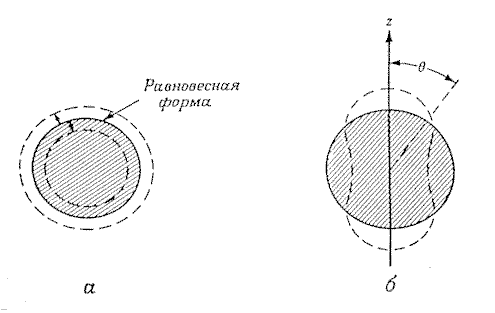
Рис. 5.1. Объемные и поверхностные
колебания ядра.
а - монопольная объемная мода: λ =
0; б - квадрупольная поверхностная мода: λ
= 2.
|
Энергию малых поверхностных
колебаний можно разложить в степенной ряд по
динамическим переменным 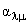 и сопряженным им скоростям
и сопряженным им скоростям 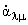 ; при этом в нее должны войти только
такие комбинации переменных и скоростей, которые
инвариантны относительно операций поворота
системы координат и обращения времени. В
частности, энергия не может содержать членов,
пропорциональных ; при этом в нее должны войти только
такие комбинации переменных и скоростей, которые
инвариантны относительно операций поворота
системы координат и обращения времени. В
частности, энергия не может содержать членов,
пропорциональных 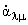 в
первой степени, так как производные по времени
меняют свой знак при обращении времени. в
первой степени, так как производные по времени
меняют свой знак при обращении времени.
Вращение системы координат не меняет
расстояния от ее начала до фиксированной точки
поверхности ядра. Из этого следует, что входящая
в выражение (5.1) сумма 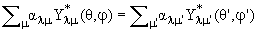
(где θ', φ' и
θ, φ - угловые переменные одной
и той же точки ядерной поверхности в повернутой
(x', y', z') и неповернутой (x, y, z) системах координат,
μ'- проекция углового
момента на ось z' и μ -
проекция на ось z) является инвариантом
относительно вращений. С другой стороны из
сферических гармоник 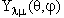 можно образовать вращательный инвариант
можно образовать вращательный инвариант 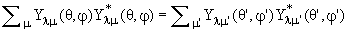 , ,
определяющий плотность вероятности угловой
волновой функции для фиксированного
пространственного направления. Сравнивая эти
два выражения, можно сделать вывод, что
динамические переменные 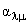 и сопряженные им скорости
и сопряженные им скорости 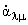 преобразуются при поворотах системы
координат точно также, как сферические гармоники преобразуются при поворотах системы
координат точно также, как сферические гармоники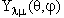 , и из них можно образовать
два (и только два) квадратичных инварианта: , и из них можно образовать
два (и только два) квадратичных инварианта: 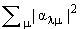 и и 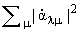 .
Следовательно, с точностью до членов второго
порядка малости по .
Следовательно, с точностью до членов второго
порядка малости по 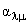 , , 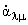 - энергия квадрупольных
колебаний поверхности ядра должна иметь вид - энергия квадрупольных
колебаний поверхности ядра должна иметь вид
где B - массовый параметри C- параметр,
характеризующий, жесткость поверхности.
Полученное выражение позволяет трактовать
динамические смещения 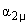 , μ = -2, -1, 0, 1, 2 как нормальные
переменные системы, каждая из которых может
совершать независимые гармонические колебания с
кинетической энергией (1/2)B| , μ = -2, -1, 0, 1, 2 как нормальные
переменные системы, каждая из которых может
совершать независимые гармонические колебания с
кинетической энергией (1/2)B|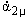 |2 и потенциальной энергией (1/2)С| |2 и потенциальной энергией (1/2)С|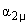 |2 (ср. с энергией
обычного одномерного гармонического
осциллятора: (1/2)m |2 (ср. с энергией
обычного одномерного гармонического
осциллятора: (1/2)m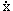 2+ (1/2)kx2).
Итак, формула (5.2) описывает энергию
пятимерного гармонического осциллятора с пятью
степенями свободы: μ = -2,
-1, 0, 1, 2. Проквантованные уровни энергии этого
осциллятора определяются соотношением 2+ (1/2)kx2).
Итак, формула (5.2) описывает энергию
пятимерного гармонического осциллятора с пятью
степенями свободы: μ = -2,
-1, 0, 1, 2. Проквантованные уровни энергии этого
осциллятора определяются соотношением
EN = (N + 5/2) ω, ω,  ω = ω = (C/B)1/2 , (C/B)1/2 , |
(5.3) |
где N - полное число квадрупольных фононов
(квантов) и  ω - энергия
квадрупольного фонона. ω - энергия
квадрупольного фонона.
Квадрупольные фононы, имеющие
целочисленный момент 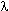 = 2 и
положительную четность, являются неразличимыми
бозе-частицами, поэтому волновая функция,
описывающая квадрупольные колебания, должна
быть симметричной относительно перестановки
фононов. Из этого вытекает, что для полного
задания произвольного состояния пятимерного
осциллятора, достаточно указать сколько имеется
квадрупольных фононов в каждом однофононном
состоянии |λ = 2,
μ>, = 2 и
положительную четность, являются неразличимыми
бозе-частицами, поэтому волновая функция,
описывающая квадрупольные колебания, должна
быть симметричной относительно перестановки
фононов. Из этого вытекает, что для полного
задания произвольного состояния пятимерного
осциллятора, достаточно указать сколько имеется
квадрупольных фононов в каждом однофононном
состоянии |λ = 2,
μ>,  = 2, 1, ..., -2 (заметим, что статистика Бозе позволяет
находиться в одном и том же состоянии
неограниченному числу бозонов). Волновая функция
многофононного состояния может быть записана в
виде |n2, n1, n0, n-1, n-2>,
где числа заполнения n2, n1, ...
указывают сколько фононов находятся в
состояниях |λ = 2,
μ = 2>, |λ = 2,
μ = 1>
, ... Введенная выше классификация волновых
функций с помощью чисел заполнения
= 2, 1, ..., -2 (заметим, что статистика Бозе позволяет
находиться в одном и том же состоянии
неограниченному числу бозонов). Волновая функция
многофононного состояния может быть записана в
виде |n2, n1, n0, n-1, n-2>,
где числа заполнения n2, n1, ...
указывают сколько фононов находятся в
состояниях |λ = 2,
μ = 2>, |λ = 2,
μ = 1>
, ... Введенная выше классификация волновых
функций с помощью чисел заполнения 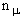 ( (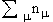 = N)
позволяет перечислить все многофононные
состояния. Однако, она имеет тот недостаток, что в
ней рассматриваются состояния, в которых не
фиксируется полный момент количества движения J
ядра. N-фононные состояния |N,...,JM> с определенным
значением полного углового момента J можно
построить, связывая моменты отдельных фононов с
учетом требований статистики Бозе. Допустимые
при данном N значения J можно найти, подсчитывая
кратность (число повторений) различных значений
z-компоненты полного углового момента M = = N)
позволяет перечислить все многофононные
состояния. Однако, она имеет тот недостаток, что в
ней рассматриваются состояния, в которых не
фиксируется полный момент количества движения J
ядра. N-фононные состояния |N,...,JM> с определенным
значением полного углового момента J можно
построить, связывая моменты отдельных фононов с
учетом требований статистики Бозе. Допустимые
при данном N значения J можно найти, подсчитывая
кратность (число повторений) различных значений
z-компоненты полного углового момента M =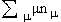 в состояниях |n2, n1,
n0, n-1, n-2> с фиксированным
числом фононов ( в состояниях |n2, n1,
n0, n-1, n-2> с фиксированным
числом фононов (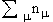 = N).
Это иллюстрирует таблица 5.1, где производится
подсчет кратности различных значений M для N =2 и 3
случаев. = N).
Это иллюстрирует таблица 5.1, где производится
подсчет кратности различных значений M для N =2 и 3
случаев.
Таблица 5.1
| Кратность различных
значений M для симметричных двух- и трехфононных
состояний пятимерного гармонического
осциллятора |
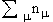 |
M |
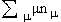
|
кратность |
J |
2 |
4 |
2·2 |
1 |
4 |
3 |
2·1+1·1 |
1 |
4 |
2 |
2·1+0·1; 1·2 |
2 |
4,2 |
1 |
2·1-1·1; 1·1+0·1 |
2 |
4,2 |
0 |
2·1-2·1; 1·1-1·1;
0·2 |
3 |
4,2,0 |
3 |
6 |
2·3 |
1 |
6 |
5 |
2·2+1·1 |
1 |
6 |
4 |
2·2+0·1; 2·1+1·2 |
2 |
6,4 |
3 |
2·2-1·1;
2·1+1·1+0·1; 1·3 |
3 |
6,4,3 |
2 |
2·2-2·1;
2·1+1·1-1·1; 2·1+0·2; 1·2+0·1 |
4 |
6,4,3,2 |
1 |
2·1+1·1-2·1;
2·1+0·1-1·1; 1·2-1·1; 1·1+0·2 |
4 |
6,4,3,2 |
0 |
2·1-1·2; 2·1-2·1+0·1;
1·1-1·1+0·1; 1· 2-2·1; 0· 3 |
5 |
6,4,3,2,0 |
|
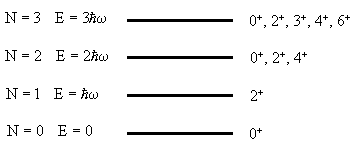 Рис. 5.2. Уровни энергии пятимерного
гармонического осциллятора.
Осцилляторный фонон имеет угловой момент 2 и
положительную четность. Уровни характеризуются
числом фононов N, энергией E и полным моментом
количества движения J. Энергия основного
состояния положена равной нулю |
Из этой таблицы видно, что при
сложении угловых моментов двух квадрупольных
фононов максимальное значение проекции M = 4
получается только 1 раз. Эту проекцию имеет
двухфононное состояние с J = 4 (см. последний
столбец). Следующая по величине проекция M = 3
также имеет кратность 1. Из этого можно сделать
вывод, что двухфононное состояние с угловым
моментом J = 3 запрещено в статистике Бозе,
так как единственное значение M = 3
исчерпывается состоянием с J = 4. Кратности
проекций M = 2 и M = 1 исчерпываются
двухфононными состояниями с моментами J = 4 и
J = 2. Следовательно, угловой момент J = 1
запрещен. Наконец, существование трех
независимых двухфононных состояний с M = 0,
позволяет утверждать, что к угловым моментам 4 и 2
должен быть добавлен момент 0. Точно также можно
показать, что симметричные трехфононные
состояния могут иметь полный момент количества
движения J = 0, 2, 3, 4, 6. Проведенное
рассмотрение подытоживает рис. 5.2, на
котором схематически изображены уровни энергии
пятимерного гармонического осциллятора. |