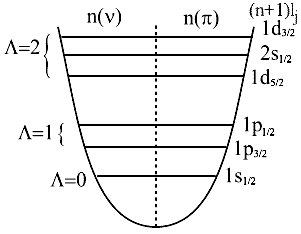
Ядерная модель оболочек
|
| Ядро | 12C | 13C | 13N | 16O |
| e = Есв/А.,МэВ | 7.67 | 7.45 | 7.22 | 7.96 |
| Еотд(n),МэВ | 18.7 | 4.95 | 20.1 | 15.66 |
| Еотд(p) ,МэВ | 15.9 | 17.4 | 1.9 | 12.13 |
Из таблицы видно, что хотя удельная
энергия связи ядра 12С меньше, чем у дважды
магического ядра 16О, энергии отделения
протонов и нейтронов для первого выше. Этот факт
и аналогичные ему являются следствием оболочечной структуры ядра. В
одночастичной модели оболочек удается, например,
объяснить, почему энергия отделения нейтрона от
ядра 13C в несколько раз меньше энергии
отделения протона от этого же ядра. Очень важным
достижением ядерной модели оболочек также
является теоретическое объяснение значений
спинов и четностей основного и возбужденных
состояний ядер.
Оболочечная модель ядра представляет
собой приложение квантовой механики к системе
нуклонов - ядру. Основу оболочечной модели ядра
(Nuclear Shell Model = SM) составляет гипотеза о том,
что взаимодействие между собой нуклонов ядра
приводит к созданию среднего
самосогласованного поля, в котором и
движутся нуклоны. Поскольку ядерные силы - силы
короткодействующие, зависимость потенциала
этого самосогласованного поля от расстояния до
центра ядра должна быть подобной зависимости от
радиуса плотности распределения ядерной
материи. Кроме того, потенциал должен быть
потенциалом притяжения. Этим условиям
удовлетворяет т.н. потенциал Вудса-Саксона
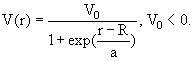 |
(2.1) |
Модель оболочек основана на предположении, что теоретическое описание ядра в основном и возбужденных состояниях может быть получено путем решения нерелятивистского уравнения Шредингера (у.Ш):
| (2.2) |
В одночастичной модели оболочек пренебрегают силами остаточного взаимодействия Vres между нуклонами и решают задачу о состояниях одной частицы (нуклона) в самосогласованном поле
| (2.2') |
Приближенное решение уравнения (2.2') может быть получено в рамках одночастичной модели оболочек (OMO). В этой простейшей модели полная волновая функция ядра как системы А нуклонов является произведением одночастичных волновых функций, которые являются решением у.Ш. для отдельного нуклона в среднем самосогласованном поле:
| (2.3) |
Простейшее модельное описание состояний нуклона в самосогласованном потенциале получено не с потенциалом Вудса-Саксона (2.1), а с более простыми потенциалами, в первую очередь с потенциалом сферически симметричного трехмерного гармонического осциллятора:
| (2.4) |
Ход решения у. Ш. с таким потенциалом
приведен в учебниках по квантовой механике (см.
например, Давыдов А.С. Квантовая механика). В
квантовой механике доказывается, что для всех
сферически симметричных потенциалов ![]() )
)
| (2.5) |
где ![]() -
сферические функции. Указанные для сферической
функции индексы отражают тот факт, что
сферические функции (а соответственно и полная
волновая функция частицы (2.5)) являются
собственными функциями операторов квадрата
орбитального момента и проекции орбитального
момента на выделенную ось:
-
сферические функции. Указанные для сферической
функции индексы отражают тот факт, что
сферические функции (а соответственно и полная
волновая функция частицы (2.5)) являются
собственными функциями операторов квадрата
орбитального момента и проекции орбитального
момента на выделенную ось:
m = ml = -l, -l+1, ..., l-1, l. Nm = 2l + 1. |
(2.6) |
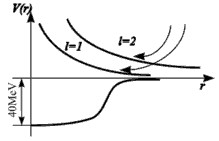 Рис. 2.1. |
Уравнение для радиальной функции содержит оператор потенциальной энергии
![]()
Вид радиальной функции R(r) и значения энергий частиц определяются радиальной зависимостью потенциала. Для потенциала (2.4)
| Rnl(r) = Nnl.(r/b)l
.exp(-r2/2b2).F(-n, l+3/2, r2/b2); Enl = |
(2.7) |
Здесь n- число узлов радиальной функции при
r > 0, F(-n, l+3/2, ![]() )- полином степени n по
)- полином степени n по ![]() = (r/b)2.
= (r/b)2.
Спектр энергий (2.7) - эквидистантный
- т.е. между состояниями с разными значениями
квантового числа ![]() одинаковые разности энергий, равные
одинаковые разности энергий, равные ![]()
![]() .
.
Часто вместо явного вида волновых
функций частицы указывают только значения
квантовых чисел, соответствующих этим функциям,
пользуясь системой обозначений, введенной Дираком:
| (2.7a) |
Однако полученные нами волновые функции, являющиеся решениями у.Ш. для 3-х мерного гармонического осциллятора, не могут считаться функциями, описывающими состояния нуклона в ядре, поскольку в этим функциях не учтен спин нуклонов. Функции, являющиеся собственными функциями оператора квадрата спина и его проекции на ось, называются спинорами. Для фермионов со спином 1/2
| (2.8) |
Волновая функция нуклона в
потенциале 3-х мерного осциллятора является
произведением функции (2.7) для осциллятора и
спинора (2.8).
Однако теоретическое описание свойств
более тяжелых ядер с потенциалом в виде (2.4)
оказалось невозможным. В частности, в этой
слишком примитивной модели невозможно объяснить
особую устойчивость ядра 12С. Дело в том, что
в предыдущих расчетах не было учтено спин-орбитальное
взаимодействие, играющее очень важную роль
в ядерных силах.
Одночастичная модель ядерных оболочек
(ОМО) основана на решении уравнения Шредингера
для нуклона в потенциале
| (2.9) |
Для того, чтобы понять роль спин-орбитального члена в потенциале (2.9), рассмотрим, какие значения может принимать полный момент нуклона
| (2.10) |
Таким образом, полный момент нуклона может принимать два значения. Решения у.Ш. для энергий нуклона в потенциале (2.9) имеют следующий вид:
| Enlj = |
(2.11) |
где ![]() Elsj = a[j(j + 1)
- l(l + 1) - s(s + 1)]/2.
Elsj = a[j(j + 1)
- l(l + 1) - s(s + 1)]/2.
Двум значениям момента нуклона
соответствуют разные вклады в энергию состояния
от спин-орбитального взаимодействия. Прежде, чем
рассчитать вклад от спин-орбитального
взаимодействия в одночастичную энергию в
формуле (2.11), выясним, какие квантовые числа
характеризуют состояния нуклона в потенциале
(2.9).
Квантовые числа, характеризующие
состояния любой квантовой системы - т.н. хорошие квантовые числа - соответствуют
собственным значениям операторов тех физических
величин, которые сохраняются в данном
потенциале. В квантовой механике доказывается,
что для сохранения физической величины
необходимо, чтобы ее оператор коммутировал с
гамильтонианом данной квантовой системы.
Если [![]() ,
,![]() ] = 0, то d
] = 0, то d![]() /dt = 0.
/dt = 0.
Для гамильтониана без спин-орбитального
члена хорошими квантовыми числами являются: E, P
(parity), l, s, ml, ms.
Полный момент нуклона и проекция
полного момента в потенциале (2.4) тоже
сохраняются. Но для гамильтониана со
спин-орбитальным взаимодействием (2.9) ситуация
меняется - проекции орбитального и спинового
моментов нуклонов не сохраняются! (Операторы
проекций орбитального и спинового моментов не
коммутируют с гамильтонианом (2.9)) Однако
проекция полного момента на выделенную ось
сохраняется. Хорошими квантовыми числами в этом
случае гамильтониана с потенциалом (2.9) являются: E,
P, l, s, j, mj.
Полученные нами выше волновые функции
нуклонов представляют собой полную систему
функций. Поэтому волновые функции, являющиеся
решениями уравнения Шредингера в потенциале со
спин-орбитальным взаимодействием, можно
разложить по этой системе функций:
| (2.12) |
Суммирование в (2.12) происходит по
всем возможным значениям проекций орбитального
и спинового моментов нуклона. Поскольку mj = ml + ms,
а проекций спина нуклона всего две, в сумму
входят не более двух членов. Коэффициенты
разложения в (2.12) называются коэффициентами Клебша-Гордона
(ККГ). Таблицы ККГ для случая s = 1/2 приведены
во всех учебниках по квантовой механике.
Распределение квантовых чисел
нуклонов по уровням энергии в потенциале (2.9)
показано на рис. 2.2
Рис. 2.2. Распределение квантовых чисел
нуклонов по уровням энергии в потенциале |
| (2.13) |
Кратность вырождения уровней равна
N = 2(2j + 1).
Пространственная P-четность волновых
функций в потенциале (2.9) такая же, что и в
потенциале без спин- орбитального члена и
определяется четностью сферической функции
| Ylm( |
(2.14) |
Пространственная четность волновой функции (2.3) ядра в одночастичной модели оболочек (ОМО) определяется произведением четностей всех нуклонов:
| (2.15) |
Таким образом, решение уравнения Шредингера
для нуклона в поле ![]()
![]() 2r2/2
+ a(
2r2/2
+ a(![]() .
.![]() ):
):
![]()
где Rnl имеет вид (2.7).
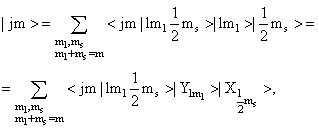
где 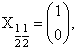
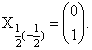
| Пример: Нуклон в 1 p3/2 с mj = m = 3/2. |
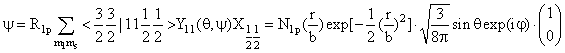
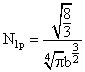 и
<jm|j'm'> =
и
<jm|j'm'> = ![]() jj'
jj'![]() mm'.
mm'.
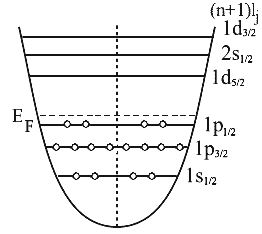 Рис. 2.3. Схема заполнения уровней в ядре 16О по одночастичной модели оболочек. |