4. Рассчитать удельные ионизационные потери энергии для протонов с энергией 10 МэВ в алюминии.

    Полная энергия частицы

 ,

откуда

и  .

Отношение кинетической энергии частицы T к энергии покоя Mc² обозначим как α, тогда

α = 10 МэВ/938.3 МэВ = 0.0107, β² = 0.021, ρ_Al = 2.7 г/см³.
Подставляя найденные значения в формулу (4), получаем:

= 92.314 МэВ/см.

    Обратим внимание, что вклад последнего члена в скобках очень мал и им можно пренебречь при небольших кинетических энергиях частиц.
    При анализе формулы (1) также можно заметить, что при β² << 1 два последних слагаемых являются малыми поправками к первому и взаимно компенсируют друг друга. Действительно, используя разложение в ряд Тейлора, можно получить:

ln(1 − β²) − β² = −(−β² + β⁴/2 +...) − β²  ≈ −β⁴/2 → 0  при β² << 1.

Проиллюстрируем это, проведя расчет вышеописанной задачи по формуле (3). Получим тот же результат: 92.314 МэВ/см, при этом вклад каждого из членов формулы

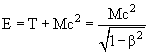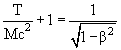
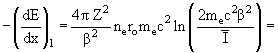92.310 МэВ/см
0.407 МэВ/см
-0.403 МэВ/см

Можно показать, что роль двух последних слагаемых становится заметной, когда кинетическая энергия частицы превышает ее энергию покоя.