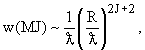Гамма-излучение ядер

5. Гамма-излучение ядер

    Явление γ-излучения ядер состоит в том, что ядро (A,Z) испускает g квант без изменения массового числа А и заряда ядра Z. Испускание γ-излучения обычно происходит после α- или β-распадов атомных ядер, если образовавшееся ядро образуется в возбужденном состоянии.
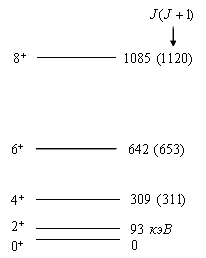
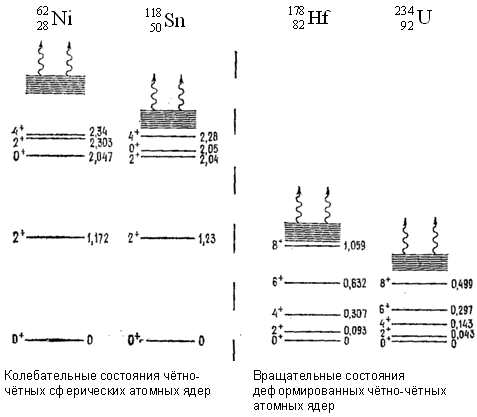
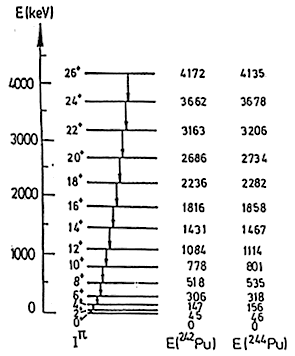
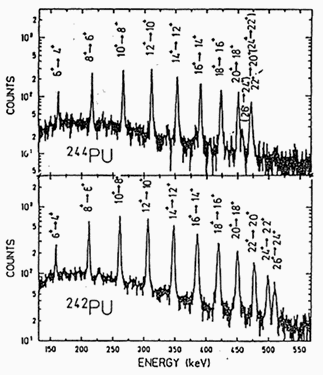
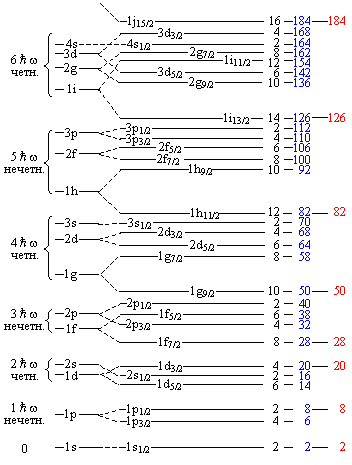
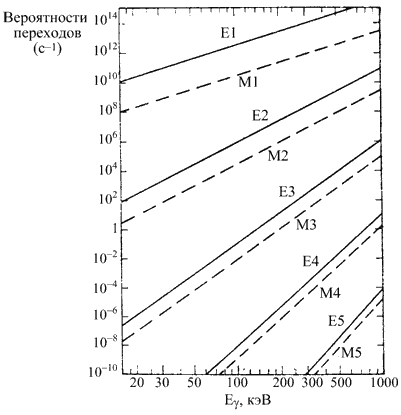
    Гамма-излучение возникает при распаде возбужденных состояний ядер. Спектр γ-излучения всегда дискретен из-за дискретности ядерных уровней. С точностью до незначительной энергии отдачи ядра энергия γ-перехода равна разности энергий уровней, между которыми происходит γ-переход. Изучая γ-спектры, получают информацию о таких свойствах атомных ядер, как деформация атомного ядра, спаривание тождественных нуклонов, структура и последовательное заполнение ядерных оболочек и др.
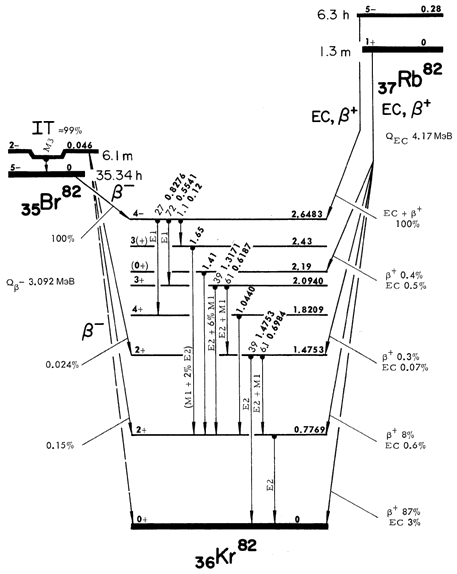
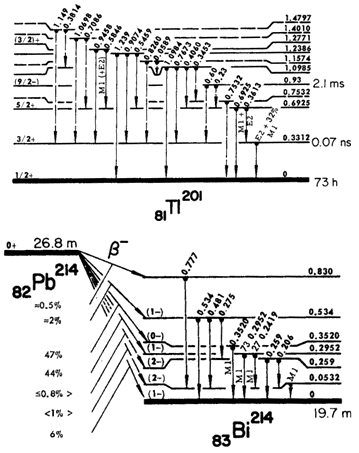
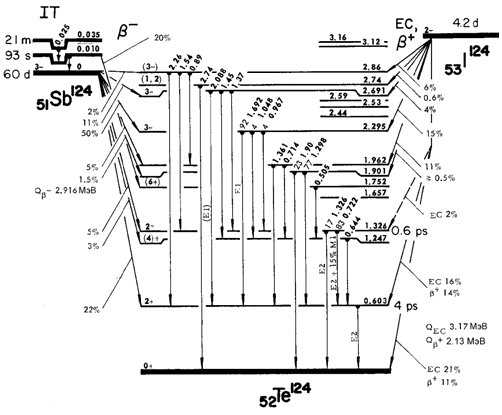
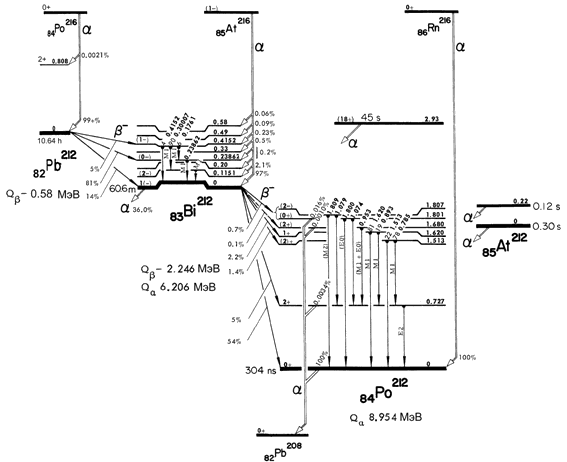
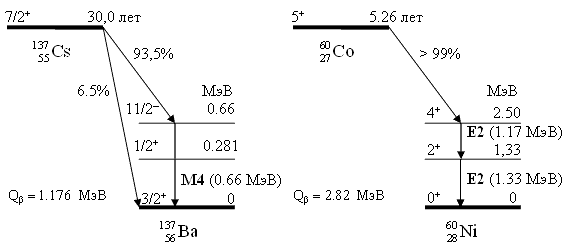
    Простейший и наиболее часто используемый способ получения γ-радиоактивных ядер основан на β-распаде на возбужденные уровни конечного ядра.
    Гамма-излучение ядер обусловлено взаимодействием нуклонов ядра с электромагнитным полем. Несмотря на это, в отличие от β-распада, γ-излучение - явление не внутринуклонное, а внутриядерное. Изолированный свободный нуклон испустить или поглотить γ-квант не может из-за совместного действия законов сохранения энергии и импульса. В то же время внутри ядра нуклон может испустить γ-квант, передав при этом часть импульса другим нуклонам.
    Времена жизни γ-радиоактивных ядер обычно изменяются от 10^-8 с до 10^-17 с, т. е. в среднем они значительно меньше времен жизни по отношению к α- и β-распадам. Причина в том, что интенсивность электромагнитных взаимодействий всего лишь на три порядка слабее ядерных. Время жизни γ-радиоактивных ядер зависит от различия спинов и четностей начального и конечного состояний, между которыми происходит γ-переход. Обычно это различие проявляется в том, что испускание частиц низких энергий с большими угловыми моментами оказывается затрудненным. В то же время зависимость вероятности γ-перехода от энергии γ-перехода менее резкая, чем у α- и β-активных. Поэтому каскадные переходы из возбужденного состояния ядра в основное являются скорее правилом, чем исключением.
    Гамма-переходы происходят между ядерными состояниями, характеризующимися определенными значениями спина J_i, J_f и чётности P_i, P_f. Поэтому γ-кванты также имеют определённые значения спина J_γ и четности P_γ. Законы сохранения момента количества движения J и четности P в электромагнитных переходах

_f =

_i +

_γ или |

_f −

_i| ≤

_γ ≤

_f +

_i,
P_f = P_i ·P_γ или P_γ = P_i ·P_f.

5.1)

определяют спин J_γ и четность P_γ, уносимую γ-квантом.

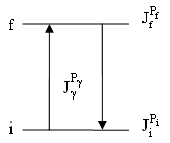
Рис. 5.1. Гамма-переходы между двумя уровнями ядра i ↔ f.

Обычно используется классификация γ-квантов по полному моменту количества движения J и четности P. Полный момент количества движения γ-кванта J принимает целочисленные значения, начиная с единицы: J= 1, 2, 3, ... . Значение J = 0 для γ-кванта исключено, так как оно отвечает сферически симметричному состоянию, а электромагнитная волна поперечна. Число J называется мультипольностью γ-кванта. В частности, низшие мультиполи имеют следующие названия: диполь – J= 1, квадруполь – J= 2, октуполь – J= 3. Спин γ-кванта J равен 1, т. е.

J(спин γ-кванта) = 1.

В зависимости от чётности при определенном значении полного момента J γ-кванты различают по типу на магнитные и электрические:

P = (-1)^J+1 – магнитные γ-кванты (МJ);
P = (-1)^J – электрические γ-кванты (ЕJ).

Для γ-квантов определенного типа и мультипольности используются следующие обозначения: сначала ставится буква Е для электрического γ-кванта и буква М для магнитного. Затем пишется цифра, равная полному моменту J γ-кванта. Например, электрический дипольный γ-квант обозначается через Е1, магнитный дипольный – через М1, электрический квадрупольный – через Е2, и т. д.
Названия «магнитный» и «электрический» происходят от типа систем зарядов и токов, излучающих соответствующие γ-кванты. Так, при колебании электрического диполя испускаемое электромагнитное излучение с квантовой точки зрения состоит из E1 γ-квантов. Колеблющийся магнитный диполь испускает M1 γ-кванты и т. д.

Правила отбора по чётности для γ-переходов имеют вид:

P_i ·P_f = (-1)^J для EJ γ-квантов;
P_i ·P_f = (-1)^J+1 для MJ γ-квантов.

(5.2)

Ядра-изобары A = 212, 216.

Рисунок демонстрирует сложные цепочки α-, β- и γ-переходов между ядрами-изобарами A = 212.

α-распада изотопов ²¹⁶Rn, ²¹⁶At, ²¹⁶Po происходят, как правило, в основное состояние ядер-продуктов. Распады на возбуждённые состояния E* > 0.2 МэВ составляют меньше 1%.
β^--распады изотопа ²¹²Bi происходят на возбужденные состояния ²¹²Po вплоть до энергии E* = 1.8 МэВ.
Возбужденные состояния изотопа ²¹²Po распадаются как в результате γ-переходов так и в результате α-распада. Аналогичная ситуация имеет место и в изотопе ²¹²At.
Вероятность α-распада основного состояния ²¹²At J^P = (1^-) близка к 100%. Вероятность е-захвата < 0.03%, вероятность β^--распада 2·10^-6%. Энергии соответствующих распадов Q(α) = 7.8 МэВ, Q(e-захв) = 1.7 МэВ,
Q(β^-) = 0.02 МэВ.
Изомерное состояние E* = 0.22 МэВ, J^P = 9^- с вероятностью >99% распадается с испусканием α-частиц. Вероятность изомерного перехода IT < 1%.

Испускаемые ядрами γ-кванты обычно имеют энергии Е от десятков кэВ до нескольких МэВ, т. е. их приведенные длины волн

[см]= ћc/E = 2·10^-11/E[МэВ]

(5.3)

лежат в интервале от 10^-9 до 5·10^-12 см. Отношение радиуса ядра R к приведенной длине волны γ-кванта почти всегда много меньше единицы:

R/ <<1.

Благодаря этому здесь, как и в случае β-распада, высшие мультиполи всегда подавлены, и в основном происходят переходы минимальной мультипольности, допустимые законами сохранения момента и четности. Вероятности вылета (или поглощения) магнитных и электрических фотонов подчиняются следующим приближенным соотношениям

(5.4)

(5.5)

    Формулы (5.4) и (5.5) дают представление о том, как зависит вероятность электромагнитного перехода от типа и мультипольности излучения. Для получения абсолютных значений вероятностей перехода нужно в каждом конкретном случае знать волновые функции начальных и конечных состояний атомных ядер. Эти волновые функции могут быть получены в рамках различных модельных представлений о ядре. В одночастичной модели оболочек предполагают, что поглощение (испускание) ядром фотона происходит при переходе только одного нуклона. Можно получить волновые функции начального и конечного состояния ядра при таком переходе и тем самым рассчитать вероятности одночастичных переходов.
    Результаты одного из таких расчетов приведены на рис. 5.2. Расчет выполнен для ядра с A = 100 в предположении, что в γ-переходе участвует один протон. Результаты расчета подтверждают выводы о доминировании g переходов с наименьшей мультипольностью.
    Формулы (5.4), (5.5) и данные рис. 5.2 позволяют предсказать, какие фотоны будут доминировать при смешанных γ-переходах и как возбуждённое ядро, испуская фотоны, будет переходить в основное состояние. Так при переходе 1/2⁺→3/2^-излучение будет смесью Е1+М2. Однако переход M2 сильно запрещен (подавлен) по сравнению с E1. Поэтому излучение будет практически целиком электрическим дипольным E1.

Эффект Мессбауэра

Естественная ширина Г ядерных уровней мала по сравнению с энергией отдачи R ядра-излучателя (источника) или ядра-поглотителя (мишени). Например, естественная ширина Г первого возбужденного уровня ядра ⁵⁷Fе, расположенного при энергии возбуждения E = 14.4 кэВ, равна ћ/τ = 4.6·10^-9 эВ (измеренное среднее время жизни τ = 98 нc), тогда как при испускании и при поглощении γ-квантов это ядро приобретает энергию отдачи T_R ~ Е²/2Мс² ~ 0.02 эВ (где М – масса атома ⁵⁷Fе). Резонансное поглощение может иметь место только в том случае, когда энергия отдачи ядра R меньше ширины ядерного уровня При переходе от свободных ядер к ядрам, связанным в кристаллической решетке, ситуация качественно изменяется. В этом случае импульс отдачи получает не отдельное ядро, а весь кристалл, в котором находится ядро, испускающее γ-квант. Это явление получило название эффекта Мессбауэра. Чтобы наблюдать резонансное поглощение мишенью из ⁵⁷Fе γ-квантов, испускаемых источником из ⁵⁷Fе, нужно скомпенсировать энергию отдачи ядер, которая в сумме составляет 2T_R. Один из способов такой компенсации состоит в том, что радиоактивный источник закрепляют на движущемся устройстве и подбирают его скорость так, чтобы разница 2T_R компенсировалась за счет эффекта Доплера. Ширина ядерных уровней столь мала, что источник нужно перемещать со скоростью, составляющей всего лишь десятые доли сантиметра в секунду.
С помощью метода резонансной флюоресценции можно измерять энергию с относительной точностью ΔЕ/Е ~ 10^–15–10^–17. По смещению линий мессбауэровских спектров определяют молекулярную структуру химических соединений, изучают сверхтонкую структуру спектров, обусловленную электрическим квадрупольным и магнитным дипольным моментами ядер. Уникальные характеристики мессбауэровских спектров используются при анализе физических и химических свойств твердых тел. Эффект Мессбауэра имеет многочисленные применения в медицине и биологии.

Рис. 5.2. Вероятности протонных γ-переходов (в с^-1) в зависимости от энергии g квантов различных мультипольностей

Внутренняя конверсия γ-квантов

Атомное ядро, находящееся в возбужденном состоянии может в результате взаимодействия с электронами атомных оболочек передать энергию возбуждения непосредственно электрону. Этот процесс называется внутренней конверсией γ-квантов. С наибольшей вероятностью внутренняя конверсия происходит на электронах ближайших к ядру K- и L-оболочек. Электрон вылетает из атома с кинетической энергией E_e.

E_e = E* − I_связи,

(5.6)

где E* − энергия возбуждения ядра, I_связи − энергия связи электрона на соответствующей оболочке атома.
Из соотношения (5.6) следует, что спектр электронов внутренней конверсии дискретный в отличие от спектра электронов β-распада. Вероятность внутренней конверсии уменьшается с увеличением энергии возбуждения ядра и увеличивается с увеличением мультипольности γ-перехода и увеличением заряда ядра Z. Измерение энергии конверсионных электронов даёт информацию о возбужденных состояниях ядер – их энергии, спине и четности. Испускание электронов внутренней конверсии сопровождается характеристическим рентгеновским излучением.

Как возникла модель сфероидальных ядер
Дж. Рейнуотер

    В первой половине 1949 г. три группы в одном и том же выпуске «Physical Review» представили различные «объяснения» оболочечной структуры ядра. Из них работа Марии Майер представляет принятую теперь, модель. Похожее предложение И. Г. Д. Иенсена с сотрудниками было опубликовано в то же время. За эти работы Майер и Иенсену была присуждена Нобелевская премия по физике в 1963 г.
    Я был весьма заинтересован моделью оболочек, предложенной Майер, поскольку эта модель неожиданно позволила понять большое количество экспериментальных данных о спинах, о магнитных моментах изомерных состояний, о систематике β-расиада и «магические числа» при Z, N = 2, 8, 20 (28), 50, 82, 126.
    Наблюдается качественное согласие, с моделью «оболочек Майер – Иенсена, значения моментов проходят через нуль при заполнении нейтронных и протонных оболочек. Для ядер с заполнённой оболочкой плюс один протоп с очень высоким значением орбитального момента квадрупольные моменты отрицательны, как и ожидалось, так как протон располагается на экваториальной орбите. При удалении нуклонов из заполненных оболочек с высоким^-значением l значение Q возрастает и становится положительным, достигая максимального значения при заполнении орбиты с данным l почти наполовину и убывая при_дальщейшем уменьшении числа нуклонов. Проблема заключалась в том, что знaчение Q/R² при R =1,5·10^–12 см достигает 10 для ядра ¹⁷⁶Lu, что в 30 раз превышает значение, которое можно было бы ожидать на основе волновых функций для сферического потенциала модели оболочек, связанных таким образом, чтобы дать состояние 7^– (Z = 71, N = 105, τ = 4·10¹⁰ лет). Для ядер редкоземельной области наиболее часто встречаются значения Q, сильно превышающие ожидаемые величины.
    Одним из интересныx свойств, даваемых моделью оболочек для деформированного ядра, является возможность прохождения внутренней энергии через минимум при возрастании деформации. Затем внутренняя энергия возрастает, пока энергия орбиты, вначале расположенной при большей энергии, но убывающей быстрее с деформацией, не пересечет последнюю заполненную вначале орбиту и не станет определять наименее связанное заполненное состояние.

УФН, т.120, вып. 4, стр. 529 (1976)

Вращательное движение в ядрах
О. Бор

    Трудно сегодня полностью представить то потрясение, которое испытали физики, воспитанные на представлениях модели жидкой капли и модели составного ядра, на которых основывалась интерпретация ядерных явлений в течение предыдущего десятилетия, в связи с обнаружением оболочечной структуры ядра.
    Значение магнитных моментов в то время представлял собой один из наиболее обширных количественных классов данных по свойствам ядер. Эти данные требовали разъяснения от теории. Значения моментов обнаруживали сильную корреляцию с предсказаниями одночастичной модели, однако вместе с тем наблюдались существенные отклонения, которые свидетельствовали о наличии некоторого не включенного в рассмотрение эффекта.
    Ключ к пониманию отклонений схемы связи угловых моментов в ядре от предсказаний одночастичной модели дало обнаружение у многих ядер большого квадрупольного момента, более чем на порядок превышающего одночастичные значения. Из этого факта непосредственно следовало распределение углового момента между многими частицами, что, казалось, подразумевало нарушение применимости одночастичной модели. Однако основные черты одночастичной.модели могут быть сохранены, если предположить, наличие отклонения от сферической симметрии у среднего ядерного поля, в котором движется нуклон. Такая картина приводит к модели ядра, напоминающей модель молекулы. В этой модели сердцевина ядра обладает колебательными и вращательными степенями свободы. По-видимому, нет никакого основания ожидать, что вращательное движение является классическим движением твердого тела. Однако вследствие большого числа нуклонов, участвующих в образовании деформащш, частота вращения должна быть мала по сравнению с частотой движения отдельных частиц.
    В этот момент существенной поддержкой для обсуждаемых работ явилось следующее открытие. Оказалось, что схема связи, характеризующая сильно деформированные ядра с четко выраженной полосой вращательных состояний, реализуется для обширного класса ядер. Первое указанно было получено Гольдхабер и Саньяром, которые обнаружили, что вероятности электрических квадрупольных переходов для распада низколежащих возбужденных состояний в четно-четных ядрах в ряде случаев были значительно больше соответствующих значений для одночастичных переходов. Это свидетельствовало о наличии коллективных видов возбуждения. Вскоре стали накапливаться указания на то, что рассматриваемые возбуждения являются частью последовательности уровней с угловыми моментами J = 0, 2, 4… и энергиями, пропорциональными J (J + 1).

УФН, т.120, вып. 4, стр. 544 (1976)

Вращательные состояния атомных ядер

Нижние вращательные уровни ядра ¹⁸⁰Hf.
Рядом с экспериментальными значениями энергии приведены энергии, рассчитанные по формуле ћ²J(J+1)/2I с моментом инерции I, оцененным по энергии состояния 2⁺

Волновой функцией вращающегося ядра является собственная функция оператора квадрата полного момента ², имеющего собственные значения ћ²J(J+1), т.е. сферическая функция Y_JM(θ,φ). Волновая функция ядра, имеющего форму аксиально-симметричного эллипсоида, не изменяется при пространственной инверсии, (отражении в плоскости xy), т. е. переходит сама в себя (см. рис. 6.25). Поэтому волновая функция такого ядра симметрична, что исключает состояния с J = 1, 3, 5, ... . Чётность сферической функции равна (-1)^J. Поэтому чётность вращательных состояний четно-четного ядра всегда положительна.
Характерным признаком вращательных уровней (помимо последовательности значений их спинов-чётностей J^Р= 0⁺, 2⁺, 4⁺, 6⁺, 8⁺, ... для чётно-чётных ядер) является пропорциональность энергии этих уровней величине J(J+1).

Кулоновское возбуждение вращательных состояний атомных ядер

Многие ядра имеют несферическую форму. Несферические ядра, обладающие осевой симметрией, имеют вращательную степень свободы, которой соответствует система вращательных уровней. Поскольку в тяжелых ядрах масса и размер ядра велики, даже при небольших деформациях вращательный уровень обычно является наиболее низколежащим. Энергии вращательных уровней Е_вр аппроксимируются соотношением

E_вр = αJ(J-1) + βJ²(J+1)².

В реакциях с тяжёлыми ионами возбуждаются вращательные состояния ядра-мишени с большими угловыми моментами. Отклонение теоретически рассчитанного спектра возбуждения для аппроксимации

E(кэВ) = 7.45 J(J+1)

от экспериментально наблюдаемых значений максимально для состояния 14⁺ и составляет ~10%.
При двухпараметрической аппроксимации

E(кэВ) = 7.45 J(J+1) − 3.4·10^-3J²(J+1)²

экспериментальный спектр описывается в пределах точности измерений.

Элементарные виды возбуждения в ядрах
Б. Моттелъсон

    Когда я впервые приехал в Копенгаген в 1950 г., было известно, что в ядрах иногда имели место явления, обусловленные независимым движением частиц, тогда как в других явлениях, например, в процессе деления и в проблеме больших квадрупольных моментов, несомненно, проявлялось коллективное поведение всего ядра как целого.
    Большой класс спектров имеет черты, соответствующие квадрудольным колебаниям относителъно сферически симметричной формы. Существование статической деформации в некоторых классах ядер получило дальнейшее решающее подтверждение в успешной классификации соответствующих состояний этих спектров в терминах одночастичного движения и надлежащим образом деформированном потенциале.
    Замечательной особенностью развивающейся картины ядерных спектров возбуждения было разделение на классы ядер сферической формы и ядер с большими деформациями.
    В то время как в образовании низкочастотных спектров доминируют переходы частиц внутри частично заполненных оболочек, с возбуждением замкнутых оболочек связаны новые виды ядерной динамики. Классическим примером коллективного возбуждения этого типа является «гигантский дипольный резонанс».
    Центральным элементом в анализе элементарных видов возбуждения и их взаимодействий является связь частицы с колебанием, которая выражает вариации среднего потенциала, связанные с коллективной колебательной амплитудой. Эта связь представляет собой организующий элемент, который генерирует самосогласованные коллективные типы возбуждений из возбуждений частиц. В то же время она приводит к взаимодействиям, которые дают естественный предел для анализа в терминах элементарных видов возбуждения.

УФН, т.120, вып. 4, стр. 563 (1976)

Квадрупольные колебания атомных ядер

Сравнение спектра низколежащих состояний ядра ¹¹⁴Cd (справа)
с идеальным спектром нижних квадрупольных колебаний поверхности (слева)

В случае квадрупольных колебаний ядерной поверхности (J = 2) угловая зависимость формы ядра дается сферическими функциями Y2M(θ,φ), которые описывают состояния, имеющие момент количества движения J = 2 и положительную четность. Поэтому каждый квадрупольный квант (фонон) также имеет момент количества движения J = 2 и положительную четность. В общем виде энергию возбуждения ядра, в котором одновременно происходят различные поверхностные колебания формы, можно записать в виде

где n_J − число фононов определенного типа, а ћω_J − энергия фонона.
Если основное состояние ядра имеет характеристики 0⁺, то первым возбужденным состоянием 2⁺ должен быть уровень, отвечающий одному квадрупольному фонону с энергией ћω₂. Предсказание о том, что первый возбужденный уровень имеет характеристики 2⁺, выполняется почти для всех сферических ядер. Двухфононный уровень должен находиться при энергии 2ћω₂. Более высокие квадрупольный возбуждения будут появляться с интервалом ћω₂в соответствии с увеличением числа квадрупольных фононов: 3ћω₂, 4ћω₂и т.д.
Для двух, трех и более квадрупольных фононов возможны не все состояния, разрешаемые правилами сложения квантовомеханических моментов количества движения. Так для двух квадрупольных фононов возможны лишь состояния с характеристиками 0⁺, 2⁺ и 4⁺. Состояния с моментами 1 и 3 запрещены в силу ограничений, накладываемых статистикой Бозе-Эйнштейна на волновую функцию двух тождественных фононов. Поэтому из двух квадрупольных фононов в чётно-чётном ядре формируются лишь возбуждения с J^P = 0⁺, 2⁺ и 4⁺, в идеальном случае вырожденные по энергии. Аналогично этому отсутствуют состояния трех квадрупольных фононов с моментами 1 и 5.

Возбужденные состояния 2⁺

В зависимости положения первого 2⁺ уровня от массового числа А отчётливо проявляются эффекты, обусловленные деформацией атомного ядра. Энергия первого 2⁺ уровня в деформированных ядрах имеет гораздо меньшие значения, чем энергия колебательного 2⁺ уровня. В ядрах, имеющих заполненные оболочки, энергия 2⁺ уровня превышает 1 МэВ.
Спектр возбуждённых состояний атомных ядер имеет сложную природу. Он является суперпозицией одночастичных возбуждений, коллективных вращательных и колебательных возбуждений. Лишь в очень ограниченном числе ядер доминирует какая-либо одна из вышеперечисленных ветвей возбуждений. Характерные энергии одночастичных возбуждений в ядрах – мегаэлектронвольты, вибрационных – сотни-тысячи килоэлектронвольт, вращательных – десятки-сотни килоэлектронвольт.

Одночастичные состояния в деформированных ядрах

Для того чтобы получить одночастичные состояния в деформированных ядрах, необходимо решить уравнение Шредингера для нуклона, находящегося в потенциальной яме, имеющей форму вытянутого или сплюснутого аксиально-симметричного эллипсоида. Конкретные расчеты были выполнены для аксиально-симметричного потенциала гармонического осциллятора – потенциала Нильссона.

    Положение одночастичных уровней в потенциале Нильссона зависит от величины и знака параметра деформации β.
    В сферически-симметричной потенциальной яме состояния нуклона характеризуются квантовыми числами орбитального l и полного моментов j = l ±1/2, причем уровни вырождены по проекции момента на ось z, т.е. кратность вырождения равна 2j+1. В деформированном ядре состояния нуклона нельзя характеризовать квантовыми числами l и j. Однако так как сохраняется симметрия относительно поворотов вокруг оси (аксиальная симметрия), то момент количества движения, создаваемый нуклоном, характеризуют квантовым числом K проекции момента на ось симметрии z.
    Деформация частично снимает вырождение, присущее одночастичным уровням сферического потенциала, расщепляя состояния с разными значениями модуля K. В силу симметрии ядра относительно отражения в плоскости симметрии состояния с +K и -K остаются вырожденными, и их характеристики описываются квантовыми числами K^p.