10. Кластерная радиоактивность
Явление испускания
α-частиц
радиоактивными ядрами хорошо известно. Возможно ли самопроизвольное испускание
каких-то других атомных ядер, отличных от ядер 4He?
Положительный ответ на этот вопрос был дан в 1984 году. Двумя независимо друг от
друга работающими группами в Англии [H.J. Rose,G.A. Jones Nature 1984, vol 307
245-247] и CCCP [Д.В. Александров и др. Письма в ЖЭТФ 1984 т.40 152-154] был
обнаружен радиоактивный распад 223Ra
с вылетом ядер 14C.
223Ra → 14C + 209Pb + Q
(31.85 МэВ).
Из
экспериментов следовало, что вероятность испускания ядер
14C почти на 10 порядков меньше чем вероятность
испускания
α-частиц.
Ядра 14C детектировались
ΔE-E
телескопом полупроводниковых детекторов, что позволило надежно отделить случаи
многократных наложений α-частиц
и дискриминировать ядра 14C
по их заряду и массе. Оба эксперимента дали практически совпадающие отношения
вероятности испускания ядер 14C
к вероятности
α-распада
λC/λα = (8.5±2.5)·1010
и
λC/λα = (7.6±3.0)·1010.
Решающим фактором, который привел к открытию кластерной радиоактивности, был
выбор распадающегося изотопа. Максимальный выигрыш в энергии получается в том
случае, если в результате кластерного распада образуется изотоп близкий к дважды
магическому изотопу 208Pb.
При этом повышается вероятность прохождения кластера через потенциальный барьер,
что увеличивает вероятность распада с образованием определенного кластера.
Спонтанный вылет ядер 14C был
вскоре обнаружен в изотопах 221Fr,
221Ra, 222Ra.
В настоящее время известно свыше 10 изотопов, для которых обнаружена кластерная
радиоактивность. Наряду с испусканием ядер 14C
наблюдалось испускание ядер 24Ne,
26Ne,
28Mg,
32Si.
Отношение вероятности испускания тяжелого кластера к вероятности
испускания
α-частицы
варьируется в интервале ~10-10–10-13.
Однако в отдельных случаях, например, в случае испускания изотопов
28,30Mg оно может доходить до
10-17.
Для понимания природы кластерной радиоактивности естественно сравнить это
явление с α-распадом
и сильно ассимметричным делением ядер.
При делении атомных ядер происходит сильная перестройка ядра в процессе его
развала на пару осколков. При этом деление возможно в тех случаях, когда перед
разрывом оно оказывается сильно деформированным - вытянутым. Параметр деформации
в момент разрыва почти вдвое превышает равновесное значение. В результате
разрыва образуется сильновозбужденные деформированные осколки. Процесс их
разлета оказывается над или околобарьерным. На рис. 10.1 приведены логарифмы
периодов полураспада в случае кластерного распада и спонтанного деления в
зависимости от параметра делимости Z2/A
для нескольких изотопов. Видно, что эта зависимость для спонтанного деления, как
правило, имеет колоколообразный вид, в то время как для кластерной
радиоактивности периоды полураспада резко уменьшаются с увеличением параметра
делимости.
Альфа-распад принципиально отличается от деления несколькими признаками.
- Процесс
α-распада
существенно подбарьерный.
- При развале исходного ядра на α-частицу
и ядро-продукт последнее как правило образуется в основном или
слабовозбужденном состоянии.
- В результате α-распада
не происходит сильной перестройки исходного ядра.
Константа кластерного распада λ или
период полураспада T1/2
определяется вероятностью образования кластера на поверхности
остаточного ядра в единицу времени w и вероятностью
прохождения сквозь потенциальный барьер D.
|
λ
=
ln2/T1/2
= wD. |
(10.1) |
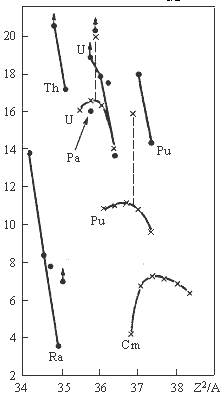
Рис. 10.1. Логарифмы периодов полураспада в случае кластерной радиоактивность
распада (точки) и спонтанного деления (крестики) в зависимости от параметра
делимости Z2/A.
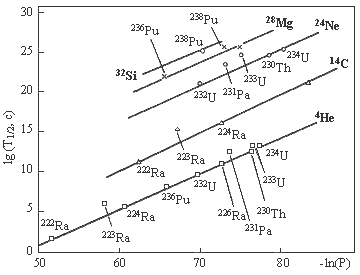
Рис. 10.2. Зависимость логарифма парциального периода кластерного распада от
логарифма проницаемости кулоновского потенциального барьера
На рис. 10.2 показана
зависимость логарифма парциального периода кластерного распада от логарифма
проницаемости потенциального барьера. Для сравнения здесь же приведена
аналогичная зависимость в случае α-распада.
Видно, что для всех случаев испускания кластеров и α-распада
наблюдается линейная зависимость.
Изучение процессов α-распада
и спонтанного деления показывает, что в обоих случаях определяющим фактором
является прохождение α-частицы
или более тяжелого кластера через потенциальный барьер. Приведенные аргументы
показывают, что кластерный распад скорее всего происходит аналогично α-распаду.
Дополнительным аргументом в пользу этого утверждения является то, что
экспериментально измеренные кинетические энергии кластеров Eкин,
вылетающих из исходного ядра достаточно хорошо определяется соотношением
где
Q
– энергия кластерного распада, Fi
– масса исходного ядра, Ft
– масса ядра продукта. Т.е. кластеры образуются преимущественно в основном
состоянии. Некоторое отклонение от соотношения (10.2) с увеличением массы
испускаемого кластера может свидетельствовать о переходе от механизма α-распада
к делительному механизму при испускании более тяжелых кластеров. Таким образом,
так же как и в случае с α-распадом
одним из главных факторов является энергия распада. Многие тяжелые ядра
оказываются энергетически неустойчивы к распаду на два ядра A → A1 +
A2.
| Q = [M(A) − M(A1) − M(A2)]c2. |
(10.3) |
Т.е. величина
Q оказывается положительной для большого числа различных
комбинаций A1и
A2.
Однако только некоторые сочетания массовых чисел A1
и A2
оказываются сильно выделены, и при распаде образуются именно эти сочетания.
Сильное влияние на энергию распада оказывают замкнутые оболочки. Энергии
кластерного распада имеют отчетливые максимумы, которые связаны с заполнением
нейтронных оболочек и подоболочек легкого фрагмента N = 8, 14, 20.
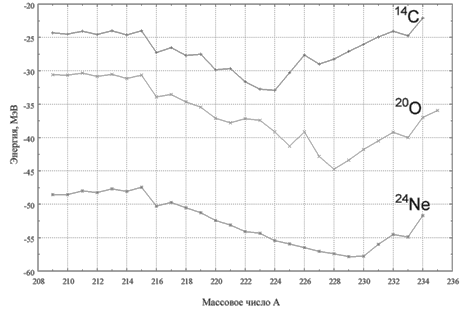
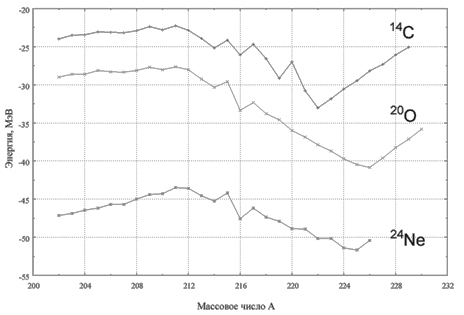
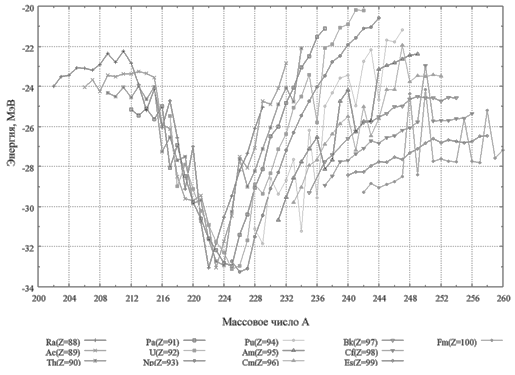
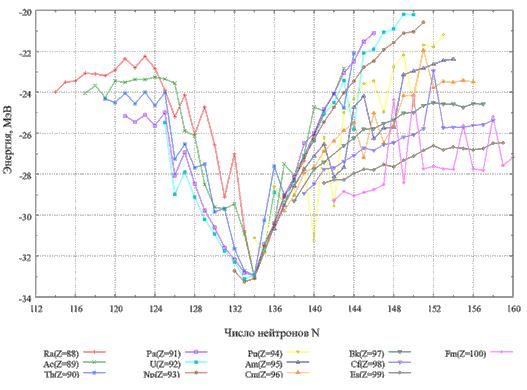
Это отчетливо видно из рис. 10.3, на котором показаны зависимости энергии
кластерного распада Q
от массы испускаемого кластера для различных распадов, приводящих к образованию
208Pb.
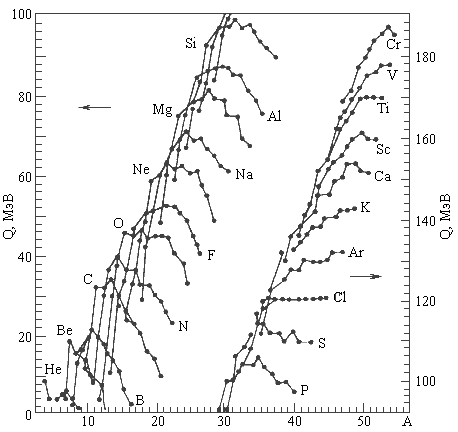
Рис. 10.3. Зависимости энергии кластерного распада Q
от массы испускаемого кластера для различных распадов, приводящих к образованию
тяжелого фрагмента 208Pb
Наиболее вероятные выходы соответствуют фрагментам с магическими числами.
Наибольшие выходы находятся при A1 = 208
(Z1 = 82,
N1 = 126)
и A2 = 14, 24, 28, 34
(N2 = 8, 14, 20).
|