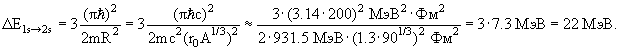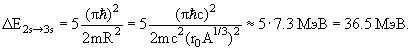Рассчитать расстояние между уровнями 1s, 2s и 3s ядра ⁹⁰Zr в случае прямоугольной потенциальной ямы бесконечной глубины и ямы гармонического осциллятора.

    В случае прямоугольной ямы

где n – главное квантовое число, m – масса нуклона, R – радиус ядра (ширина ямы). Величина расстояний между уровнями 1s, 2s и 3s будет

    Рассмотрим движение частицы в поле трехмерного осциллятора

 U(r) = mω²r²/2

В декартовых координатах решение уравнения Шредингера можно искать в виде ψ(r) = ψ₁(x)ψ₂(y)ψ₃(z), каждая из которых удовлетворяет одномерному уравнению (5.12) с энергетическим спектром (5.13)

E_i = ћω(n_i + 1/2).

Поскольку полная энергия равна сумме E_i, то

E = ћω(n₁ + n₂ + n₃ + 3/2) = ћω(N_осц + 3/2).

В данном представлении отсутствует зависимость от квантовых чисел l и m. Состояния с определенными значениями n, l и m можно найти, решая задачу в сферических координатах (см. п. 5.4). Подробное рассмотрение задачи трехмерного осциллятора можно найти в учебниках по квантовой механике. Решение уравнения (5.17) для радиальной волновой функции с заданным потенциалом определяет энергетический спектр гармонического осциллятора

E_nl = ћω(2n_r  + l  + 3/2).

Таким образом N_осц  = 2n_r  + l и уровень с заданным N_осц может иметь разные l (см. рис. 10.6). Радиальные квантовые числа n_r осцилляторном потенциале принимают целые значения, начиная с 0: n_r = 0, 1, 2,… и связаны с радиальным квантовым числом в ОМО как n = n_r + 1.

где  МэВ для 90Zr.

Расстояние будет  МэВ.

В яме гармонического осциллятора спектр уровней эквидистантный и  для энергии уровней с l = 0  определяется соотношением

E_n = ћω(2n + 3/2),

где ћω = (2V₀ћ²/(mR²))^1/2 ≈ 41A^-1/3 = 41·90^-1/3 = 9.8 МэВ для ⁹⁰Zr.
Расстояние будет ΔE_1s→2s = ΔE_2s→3s = 2ћω = 19.6 МэВ.