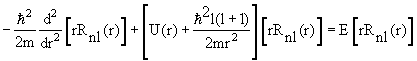Семинар 4. Уравнение Шредингера
Аналог классического волнового уравнения был предложен
Э. Шредингером в
1925 г. Как и классическое уравнение, уравнение Шредингера связывает производные
волновой функции по времени и координате. Уравнение Шредингера описывает
поведение любых нерелятивистских систем. На примерах частицы, находящейся в
бесконечно глубокой яме, и гармонического осциллятора рассмотрены простейшие
квантовые системы, получены дискретные спектры состояний. Возможности описания
динамики данных систем ограничены набором квантовых чисел, отражающих
универсальные и внутренние симметрии квантовых систем.
- 4.1. Уравнение Шредингера
- 4.2. Частица в
прямоугольной яме с бесконечными стенками
- 4.3. Гармонический
осциллятор
- 4.4. Частица в поле с
центральной симметрией
- 4.5. Орбитальный момент
количества движения
- 4.6. Спин
- 4.7. Полный момент количества движения
- 4.8. Квантовые числа
- Задачи
4.1. Уравнение Шредингера
В квантовой физике изменение
состояния частицы описывается уравнением Шредингера
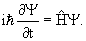 |
(4.1) |
где
 – оператор
Гамильтона – аналог классической функции Гамильтона – оператор
Гамильтона – аналог классической функции Гамильтона
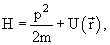
в которой
 и и
 заменены
операторами импульса заменены
операторами импульса
 x, x,
 y, y,
 z и
координаты z и
координаты
 , ,
 , ,
 : :
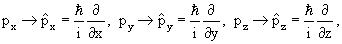
х →
 = х,
y → = х,
y →
 =
y, z → =
y, z →
 = z, = z,
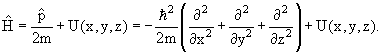 |
(4.2) |
Уравнение
Шредингера
Зависящее от времени
уравнение Шредингера:
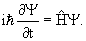
где
 –
гамильтониан системы. –
гамильтониан системы.
Разделение переменных.
Запишем Ψ( ,t)
= ψ( ,t)
= ψ( )θ(t),
где ψ является функцией координат, а θ – функция
времени. Если )θ(t),
где ψ является функцией координат, а θ – функция
времени. Если
 не
зависит от времени, тогда уравнение не
зависит от времени, тогда уравнение
 ψ
= iћψ принимает вид θ ψ
= iћψ принимает вид θ ψ
= iћψθ или ψ
= iћψθ или
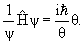
Левая часть является функцией только координат, а
правая не зависит от переменной x.
Поэтому обе части последнего уравнения должны быть равны
одной и той же постоянной, которую обозначим
E
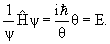
Следовательно,
θ(t) = exp(−iEt/ћ),
 ψ( ψ( )
= Eψ( )
= Eψ( )
и Ψ( )
и Ψ( ,t)
= ψ( ,t)
= ψ( )exp(−iEt/ћ). )exp(−iEt/ћ).
Уравнение
 ψ( ψ( )
= Eψ( )
= Eψ( ) называют
стационарным уравнением Шредингера. Для одномерной
системы с массой
m в поле с потенциалом
U(x)
оно принимает вид: ) называют
стационарным уравнением Шредингера. Для одномерной
системы с массой
m в поле с потенциалом
U(x)
оно принимает вид:
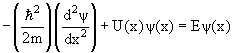 или или
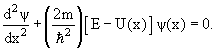
Для трехмерной системы с массой m
в поле с потенциалом U( ): ):
−(ћ2/2m)Δψ( )
+ U( )
+ U( )ψ( )ψ( )
= Eψ( )
= Eψ( ), ),
где Δ – лапласиан. |
Так как уравнение Шредингера
является линейным уравнением первого порядка по времени, то с его помощью по
заданному значению волновой функции Ψ(x,
y, z, 0) в момент времени
t = 0 можно найти её значение в произвольный момент
времени t − Ψ(x,
y, z, t).
Уравнение Шредингера для стационарного состояния, когда потенциальная энергия
частицы не зависит от времени, имеет вид
Это уравнение называют стационарным уравнением Шредингера.
Так как в стационарном состоянии
Ψ( ,t)
= ψ( ,t)
= ψ( )exp(−iEt/ћ) )exp(−iEt/ћ) |
(4.4) |
и вероятность найти частицу в момент t в точке
x, y, z
пропорциональна |Ψ( ,t)|,
то она ~ |ψ(x,y,z)|2,
т.е. не зависит от времени. Аналогично, вероятность обнаружить значение
физической величины, характеризующей систему, также не изменяется со временем,
поскольку выражается через квадрат модуля волновой функции. ,t)|,
то она ~ |ψ(x,y,z)|2,
т.е. не зависит от времени. Аналогично, вероятность обнаружить значение
физической величины, характеризующей систему, также не изменяется со временем,
поскольку выражается через квадрат модуля волновой функции.
4.2. Частица в одномерной
прямоугольной яме с бесконечными стенками
Потенциальная энергия
U(x) в прямоугольной яме удовлетворяет
следующим условиям:
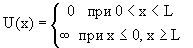 |
(4.5) |
|
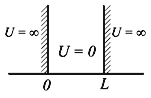
Рис.4.1. Прямоугольная яма с бесконечными стенками |
Частица находится в области 0 ≤ x ≤ L. Вне этой области ψ(x)
= 0. Уравнение Шредингера для частицы, находящейся в области 0 ≤ x ≤ L
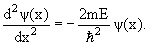 |
(4.6) |
Волновая функция, являющаяся решением уравнения (4.9), имеет вид
|
ψ(x)= Аsin
kx
+ Bcos kx, |
(4.7) |
где k = (2mE/ћ2)1/2.
Из граничных условий ψ(0) = 0, ψ(L) = 0 и условий непрерывности волновой
функции следует
kL = nπ,
n = 1, 2, 3, … , то есть внутри потенциальной ямы с бесконечно высокими
стенками устанавливаются стоячие волны, а энергия состояния частиц имеет
дискретный спектр значений En
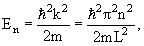 n = 1, 2, 3, …
n = 1, 2, 3, … |
(4.9) |
Частица может находиться в
каком-то одном из множества дискретных состояний, доступных для неё.
Каждому значению энергии En соответствует
волновая функция ψn(x), которая с учетом
условия нормировки
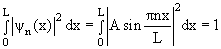
имеет вид
 |
(4.10) |
В отличие от классической, квантовая частица в прямоугольной яме не может
иметь энергию
E < ћ2π2/(2mL2).
Состояния частицы ψn в
одномерном поле бесконечной потенциальной ямы полностью описывается с помощью
одного квантового числа n. Спектр энергий дискретный.
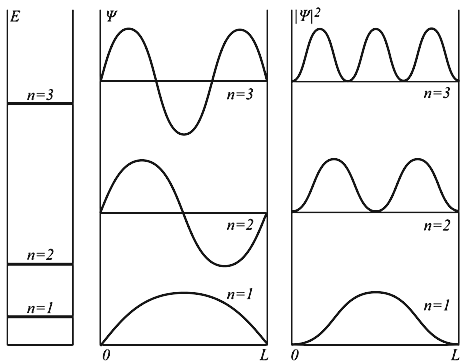
Рис. 4.2. Уровни энергии и волновые функции частицы
Ψ в бесконечной прямоугольной яме. Квадрат модуля волновой функции
|Ψ|2 определяет
вероятность нахождения частицы в различных точках потенциальной ямы.
4.3. Гармонический осциллятор
Положение уровней частицы в потенциальной яме зависит от вида потенциальной
ямы. В одномерной потенциальной яме гармонического осциллятора потенциальная
энергия имеет вид
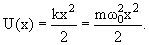 |
(4.11) |
В этом случае одномерное уравнение Шредингера имеет вид
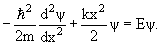 |
(4.12) |
Допустимые значения полной энергии определяются формулой
|
En = ћω0(n
+ 1/2),
n = 0, 1, 2, |
(4.13) |
В отличие от бесконечной прямоугольной ямы, спектр уровней гармонического
осциллятора эквидистантный.
С увеличением массы частицы или размеров области ее локализации квантовое
описание частицы переходит в классическое.
Частица в одномерной потенциальной яме
Одномерная прямоугольная яма шириной L:
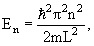
 n = 1, 2, …
n = 1, 2, …
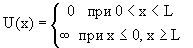
Одномерный гармонический осциллятор:
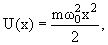 En = ћω0(n
+ 1/2),
n = 0, 1, 2, En = ћω0(n
+ 1/2),
n = 0, 1, 2, |
4.4. Частица в поле с центральной симметрией
В сферических координатах стационарное уравнение Шредингера для частицы в
центральном потенциале U(r)
имеет вид
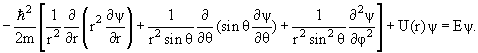 |
(4.14) |
Решение уравнения (4.14) записываются в виде произведения радиальной и
угловой функций
|
ψ(r,θ,φ)
= Rnl(r)Ylm(θ,φ), |
(4.15) |
где радиальная функция Rnl(r) и
угловая функция Ylm(θ,φ),
называемая сферической, удовлетворяют уравнениям
 2Ylm(θ,φ)
= ћ2l(l
+1)Ylm(θ,φ) 2Ylm(θ,φ)
= ћ2l(l
+1)Ylm(θ,φ) |
(4.16) |
или
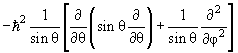 Ylm(θ,φ)
= ћ2l(l
+1)Ylm(θ,φ) Ylm(θ,φ)
= ћ2l(l
+1)Ylm(θ,φ)
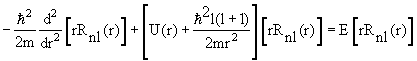 |
(4.17) |
Уравнение (4.16) определяет возможные собственные значения
l и собственные функции Ylm(θ,φ) оператора
квадрата момента  2.
Уравнение (4.17) определяет собственные значения энергии Е и радиальные
собственные функции Rnl(r),
от которых зависит энергия системы (рис. 4.3). 2.
Уравнение (4.17) определяет собственные значения энергии Е и радиальные
собственные функции Rnl(r),
от которых зависит энергия системы (рис. 4.3).
Схема уровней (последовательность и абсолютные значения энергий) зависит от
радиальной функции Rnl(r),
которая в свою очередь определяется потенциалом U(r),
в котором находится частица.
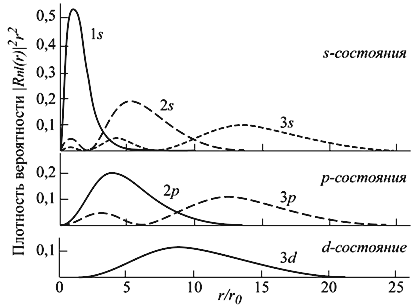
Рис. 4.3. Радиальное распределение вероятности нахождения электрона в
кулоновском поле протона (атом водорода). Расстояния даны в боровских радиусах
r0 = ћ2/mee2 ≈
0.529·108 cм.
|
Решения уравнения
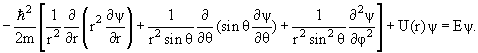
существуют лишь при
определенных значениях квантовых чисел n
(радиальное квантовое число), l (орбитальное
квантовое число) и m (магнитное квантовое число).
Возможные энергетические
состояния системы (уровни энергии) определяются числами n
и l и в случае сферически симметричных состояний
не зависят от квантового числа m. Число
n может быть только целым:
n
= 1, 2, …, ∞. Число l может принимать
значения 0, 1, 2, …, ∞. |
4.5. Орбитальный момент количества движения
Собственные значения
L2 и
Lz являются
решением уравнений
 2Ylm(θ,φ) =
L2Ylm(θ,φ) и 2Ylm(θ,φ) =
L2Ylm(θ,φ) и  zYlm(θ,φ) =
LzYlm(θ,φ). zYlm(θ,φ) =
LzYlm(θ,φ).
Они имеют следующие дискретные значения
L2 =
ћ2l(l
+ 1), где l = 0, 1, 2, 3, …,
Lz =
ћm,
где m = 0, ± 1,
± 2, ± 3,…,
± l.
Для характеристики состояний с различными значениями орбитального момента l обычно используют следующие обозначения:
Спектроскопические названия орбитальных моментов l
| l = 0 |
s-состояние |
| l = 1 |
p-состояние |
| l = 2 |
d-состояние |
| l = 3 |
f-состояние |
| l = 4 |
g-состояние |
| l = 5 |
h-состояние |
| и. т. д. |
|
Состоянию с l = 0 отвечает сферически симметричная
волновая функция. В тех случаях, когда l ≠ 0
волновая функция не имеет сферической симметрии. Симметрия волновой функции
определяется симметрией сферических функций Ylm(θ,φ).
Имеет место интересное квантовое явление, когда решение сферически симметричной
задачи (потенциал описывает сферически симметричную систему) приводит к
состояниям, не обладающим сферической симметрией. Таким образом, симметрия
уравнений не обязательно должна отражаться в симметрии каждого отдельно взятого
решения этих уравнений, а лишь во всей совокупности этих решений.
Для частицы, находящейся в сферически симметричном потенциале, величина
орбитального момента количества движения L:
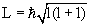 |
(4.18) |
Обычно, для упрощения, когда говорят о величине орбитального момента
количества движения, называют этой величиной квантовое число
l, имея в виду, что между l и
L имеется однозначная связь (4.18).
|
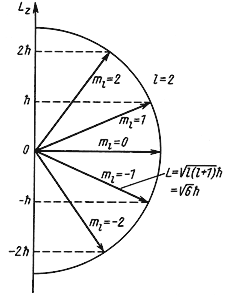
Рис. 4.4 Возможные ориентации вектора
 при
квантовом числе l = 2. при
квантовом числе l = 2. |
Так как величина l может принимать только
целочисленные значения 0, 1, 2, 3,…, то и орбитальный момент количества движения
L квантуется.
Например, для частицы с l = 2 момент
количества движения
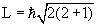 = =
= 6.58·10-22√6
МэВ·сек ≈ 2.6·10-34
Дж·сек.
Пространственное квантование. Орбитальный момент количества движения является
векторной величиной. Так как величина орбитального момента количества движения
квантуется, то и направление
 по
отношению к выделенному направлению z, например, к
внешнему магнитному полю, также квантуется и принимает дискретные значения
Lz =
ћm,
где m изменяется от +l до –l,
т. е. имеет 2l + 1 значений. Например, при
l = 2 величина m принимает
значения +2, +1, 0, -1, -2 (см. рис. 4.4). Вместе с тем энергия системы не
зависит от m, т. е. от направления вектора по
отношению к выделенному направлению z, например, к
внешнему магнитному полю, также квантуется и принимает дискретные значения
Lz =
ћm,
где m изменяется от +l до –l,
т. е. имеет 2l + 1 значений. Например, при
l = 2 величина m принимает
значения +2, +1, 0, -1, -2 (см. рис. 4.4). Вместе с тем энергия системы не
зависит от m, т. е. от направления вектора
 ,
что является очевидным следствием сферической симметрии системы. ,
что является очевидным следствием сферической симметрии системы.
Состояние частицы, находящейся в сферически симметричном поле, полностью
описывается тремя квантовыми числами: n,
l и m.
Появление квантовых чисел связано со свойствами симметрии системы. Характер
этой симметрии определяет возможные значения квантовых чисел. Очевидно, что
система, описываемая функцией eimφ, примет прежнее
значение только тогда, когда азимутальный угол φ в результате поворота вокруг
оси z примет прежнее значение φ. Этому условию функция
eimφ удовлетворяет только в случае, когда величина
mφ кратна 2π. Т.е. величина m
должна иметь целые значения. Так как необходимо учитывать вращение в двух
противоположных направлениях и отсутствие вращения, единственно возможными
значениями оказываются m = 0, ±1, ±2, … .
Спин − собственный момент количества движения частицы. Между значением
вектора спина
 и
квантовым числом спина s выполняется такое же
соотношение, как между величиной значением вектора орбитального момента и
квантовым числом спина s выполняется такое же
соотношение, как между величиной значением вектора орбитального момента
 и
орбитальным квантовым числом l: и
орбитальным квантовым числом l:
 2
= ћ2s(s + 1) 2
= ћ2s(s + 1) |
(4.19) |
В отличие от орбитального квантового числа l,
которое может быть лишь целым числом или нулем, спиновое квантовое число
s (в дальнейшем просто спин) может быть как целым
(включая нуль), так и полуцелым, т. е. s = 0, 1/2, 1, 3/2, 2, 5/2,
… , но при этом для каждой элементарной частицы спин может принимать
единственное присущее этому типу частиц значение. Так, спины π-мезонов и К-мезонов
равны 0. Спины электрона, протона, нейтрино, кварков и их античастиц равны 1/2.
Спин фотона равен 1. Бозоны составляют класс частиц с целым значением спина,
спин фермионов имеет полуцелое значение. Спин частицы невозможно изменить, также
как её заряд или массу. Это её неизменная квантовая характеристика.
Как и в случае других квантовых векторов, проекция вектора спина
 на
любое фиксированное направление в пространстве (например, на ось
z) может принимать 2s + 1
значение: на
любое фиксированное направление в пространстве (например, на ось
z) может принимать 2s + 1
значение:
szћ =
±sћ, ±(s
− 1)ћ, ±(s
− 2)ћ,...,
±1/2ћ или 0.
Число sz −
это квантовое число проекции спина. Максимальная величина sz совпадает
с s. Так как спин электрона равен 1/2, то проекция
этого спина может принимать лишь два значения sz
=
±1/2. Если проекция +1/2, то говорят, что спин направлен вверх, если
проекция -1/2, то говорят, что спин направлен вниз.
4.7. Полный момент количества движения
Полный момент количества движения частицы или системы частиц
 является
векторной суммой орбитального является
векторной суммой орбитального
 и
спинового и
спинового  моментов
количества движения. моментов
количества движения.
 = =
 + +
 . .
Квадрат полного момента имеет значение:
 2
= ћ2j(j + 1). 2
= ћ2j(j + 1).
Квантовое число полного момента j, соответствующее
сумме двух векторов
 и и
 ,
может принимать ряд дискретных значений, отличающихся на 1: ,
может принимать ряд дискретных значений, отличающихся на 1:
j = l + s, l + s −1,...,
|l − s|
Проекция  на
выделенную ось Jz также принимает дискретные значения: на
выделенную ось Jz также принимает дискретные значения:
Jz = ћjz;
= -j, -j + 1,..., j − 1, j.
Число значений проекции Jz равно 2j + 1.
Если для  и и
 определены
единственные значения проекций на ось z lz и
sz, то jz также определена
однозначно: jz = lz + sz. определены
единственные значения проекций на ось z lz и
sz, то jz также определена
однозначно: jz = lz + sz.
4.8. Квантовые числа
Квантовые числа – это целые или дробные числа, которые определяют все
возможные значения физической величины, характеризующей различные квантовые
системы – атомы, атомные ядра, кварки и другие частицы.
Таблица квантовых чисел
|
n |
Радиальное квантовое число. Определяет число узлов волновой функции и
энергию системы. n = 1, 2, …, ∞. |
|
J, j |
Полный угловой момент J и его квантовое число
j. Последнее никогда не бывает отрицательным и
может быть целым или полуцелым в зависимости от свойств рассматриваемой
системы.
 2
= ћ2j(j + 1). 2
= ћ2j(j + 1).
|
|
L, l |
Орбитальный угловой момент L и его квантовое
число l. Интерпретация l
такая же, как j, но l
может принимать только целые значения, включая нуль:
l = 0, 1, 2,…. L2 =
ћ2l(l
+ 1).
|
|
m |
Магнитное квантовое число. Проекция полного или орбитального углового
момента на выделенную ось (обычно ось z) равна mћ.
Для полного момента m = ±j,
±(j-1), …, ±1/2 или 0. Для орбитального
m = ± l, ± (l-1),
…, ±1, 0. |
|
S, s |
Спиновый угловой момент S и его квантовое
число s. Оно может быть либо положительным
целым (включая нуль), либо полуцелым. s –
неизменная характеристика частицы определенного типа.
S2 = ћ2s(s
+ 1). |
|
sz |
Квантовое число проекции спинового момента частицы на выделенную ось.
Эта проекция может принимать значения szћ,
где sz =
± s, ± (s -1), …,
±1/2 или 0. |
|
P или π |
Пространственная четность. Характеризует поведение системы при
пространственной инверсии
 →
- →
- (зеркальном
отражении). Полная четность частицы Р = π(-1)l
, где π – её внутренняя четность, а (-1)l
– её
орбитальная четность. Внутренние четности кварков положительные, антикварков - отрицательные. (зеркальном
отражении). Полная четность частицы Р = π(-1)l
, где π – её внутренняя четность, а (-1)l
– её
орбитальная четность. Внутренние четности кварков положительные, антикварков - отрицательные. |
|
I |
Изоспин. Характеризует свойство зарядовой инвариантности сильных
взаимодействий |
Для обозначения спинового момента часто используют букву J.
Все состояния, в которых может находиться квантовая система, описываются с
помощью полного набора квантовых чисел. Так в случае протона в ядре состояние
протона описывается с помощью четырех квантовых чисел, соответствующих четырем
степеням свободы – трем пространственным координатам и спину. Это
- Радиальное квантовое число n ( 1, 2, …,
∞),
- Орбитальное квантовое число l (0, 1, 2,
…),
- Проекция орбитального момента m (± l,
± (l-1), …, ±1, 0),
- Спин протона s =1/2.
Для описания сферически-симметричных систем в квантовой физике используются
различные сферически симметричные потенциалы с различной радиальной
зависимостью:
- Кулоновский потенциал U = Q/r,
- Прямоугольная потенциальная яма
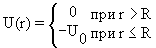
- Потенциал типа гармонического осциллятора U
= kr2,
- Потенциал Вудса-Саксона (с его помощью описываются внутриядерные
взаимодействия):
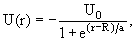
где U0,
а и R – положительные константы (R
– радиус ядра). Во всех случаях сферически симметричные системы можно
описать с помощью набора квантовых чисел n,
l, j,
jz,
однако, в зависимости от радиального вида потенциала энергетический спектр
состояний системы будет различным.
Существование сохраняющихся во времени физических величин тесно связано со
свойствами симметрии гамильтониана системы. Например, в случае, если квантовая
система обладает центральной симметрией U = U(r),
то этой системе соответствует сохранение орбитального момента количества
движения l и одной из его проекций
m. При этом из-за сферической симметрии задачи энергия состояний не будет
зависеть от величины m, т. е. состояния будут
вырожденными по m.
Наряду с пространственными симметриями, связанными с непрерывными
преобразованиями, в квантовой физике существуют и другие симметрии –
дискретные. Одной из них является зеркальная симметрия волновой функции
относительно инверсии координат ( →
- →
- ).
Оператору инверсии соответствует квантовое число четность, которое может
принимать два значения +1 и -1 в зависимости от того, сохраняется ли знак
волновой функции при инверсии или меняется на противоположный. ).
Оператору инверсии соответствует квантовое число четность, которое может
принимать два значения +1 и -1 в зависимости от того, сохраняется ли знак
волновой функции при инверсии или меняется на противоположный.
Система тождественных частиц характеризуется еще одной симметрией –
симметрией относительно перестановок тождественных частиц. Эта симметрия
определяется свойствами частиц, образующих систему. Системы частиц с целым
спином (бозонов) описываются симметричными волновыми функциями, системы частиц с полуцелым
спином (фермионов) − антисимметричными волновыми функциями.
|
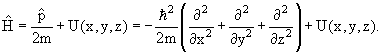
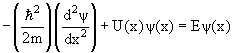 или
или
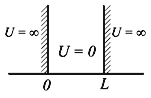

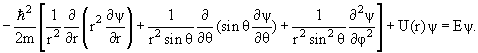
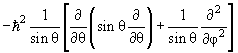 Ylm(θ,φ)
= ћ2l(l
+1)Ylm(θ,φ)
Ylm(θ,φ)
= ћ2l(l
+1)Ylm(θ,φ)